Цифрового канала связи при наличии помех

Канал связи называется цифровым, если передаваемые по нему дискретные сообщения можно представить в виде чисел. Например, при использовании двоичного кода, когда алфавит сообщений равен двум, символам x₁ и х₂ можно приписать соответственно цифры 1 и 0. Тогда кодовые комбинации, состоящие из трёх позиций, например х₁х₂х₁, x₂x₁x₂ , x₂x₁x₁ записанные в виде 001, 010, 011, можно рассматривать как цифры 1, 2, 3 в двоичном коде.

Производительность источника сообщений характеризуется ско­ростью R создаваемой информации. Аналогично можно ввести понятие R_k - скорости передачи информации канала связи с помехами

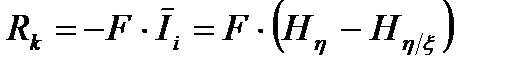, (3.9)

где I_i количество информации, переносимой одним символом сообщения по каналу связи с помехами (3.8); F - полоса пропускания канала.

Пропускной способностью С канала связи будем называть наибольшее количество информации, которое может быть передано в единицу времени по этому каналу:

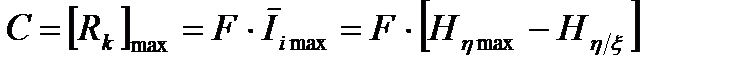. (3.10)

В общем случае для нахождения пропускной способности необхо­димо максимизировать скорость передачи. Однако если считать, что полоса пропускания канала F и эффект действия помех 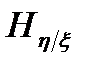заданы, то максимизация скорости передачи сводится к определению максиму­ма энтропии сообщения. Так как для дискретного сообщения максимум энтропии 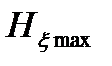зависит от алфавита, а при отсутствии помех 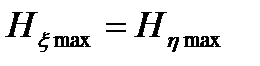, то пропускную способность цифрового канала связи можно определить выражением

. (3.11)

Найдём пропускную способность цифрового канала связи с поме­хами, по которому передаются кодовые комбинации с основанием кода, равным двум. Такой цифровой канал будем называть двоичным.

Граф двоичного канала

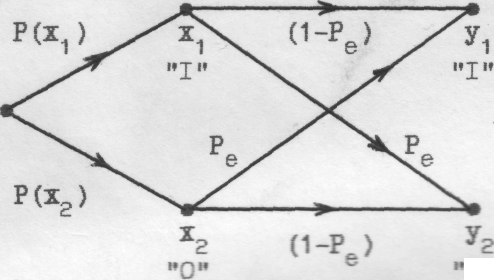
Из рассмотрения графа следует, что из-за действия помех вход­ной символ х₁("1") превращается в выходной символ у ₁("1") с вероятностью (1-Р_e), меньшей единицы, где Р_e вероятность ошибки. С вероятностью Р_e этот же символ х ("1") превращается (инвертиру­ется) в символ у₂("0"). Аналогично действует помеха и на символ x_2.

Пропускная способность двоичного канала связи согласно (3.11) будет равна

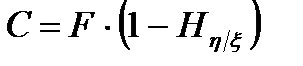, (3.12)

где учтено, что log m = log 2 = 1. Пред­полагается, что символы х₁ и х₂ и, соответственно, символы у₁, у₂ при отсутствии помех равновероятны:

.

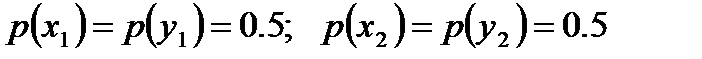Найдём условную энтропию

.

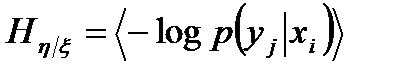Функцию 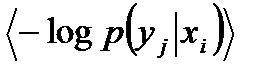будем рассматривать как функцию двух переменных х_i, у_j. Заметим, что оператор математического ожидания < • > для системы двух непрерывных случайных величин раскрывается с помощью двойного интеграла от произведения функции двух перемен­ных на двумерную плотность вероятности . Аналогично этот же оператор < • > раскрывается для системы двух дискретных случайных величин с той только разницей, что интегрирование заменяется сум­мированием по всем индексам i, j:

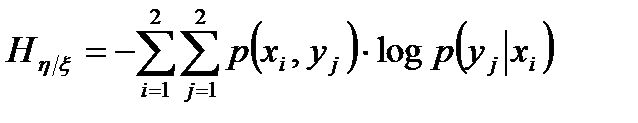, (3.13)

где р(х_i,у_j ) - двумерная вероятность символов х_i и у_j.

Так как в условиях помех символы х_i и у_j следует рассматри­вать как зависимые случайные величины, то согласно правилу произ­ведения зависимых событий имеем

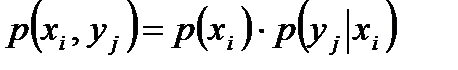. (3.14)

Подставив (3.14) в выражение (3.13), получим

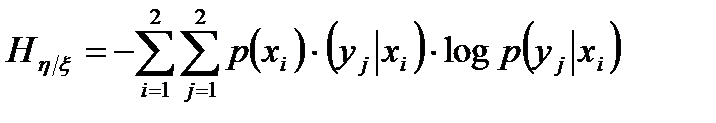, (3.15)

где сначала суммируются все члены, зависящие от индекса j, a затем все члены, зависящие от i. Заметим, что р(х₁,) = р(х₂) = 0.5, р(у₁½х₁ ) = р(у₂½х₂) = 1-Р_e , p(y₁½x₂) = p(y₂½x₁)= P_e Подставив эти данные в (3.15), получим

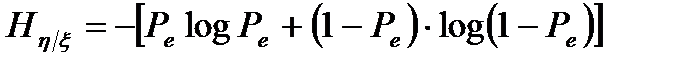. (3.16)

Подставив результат (3.16) в формулу (3.12), получим окон­чательное выражение для пропускной способности двоичного цифрово­го канала связи

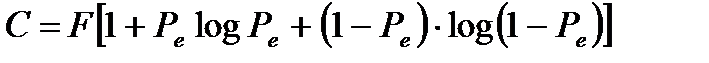, (3.17)

где F - полоса пропускания канала связи; Р_e - вероятность ошибки при передаче двоичного символа.

Пропускная способность канала связи прямо пропорциональна по­лосе пропускания F и является сложной функцией вероятности ошибки Р_e. Представляет интерес проследить зависимость С от Р_e. Эта зависимость представлена на рис.

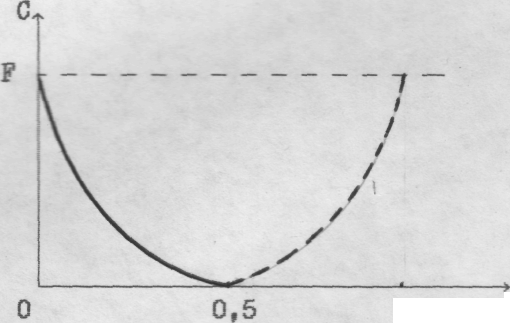
Р_e

Если Р_e = 0.5, то С = 0. Этот результат имеет ясную физическую трактовку. При Р_e=0.5 символы у₁, у₂ на выходе канала связи воссоздаются вне всякой связи с символами на входе x₁, х₂. Это означает, что через канал связи никакая информация в среднем не передаётся. Рост С, когда Р_e> 0.5, означает, что под действи­ем помех большинство символов инвертируется. И если работать в обратном коде, приписывая “1” символу y₂, а “0” символу y₁, то появляется снова возможность передавать информацию по каналу свя­зи.