Энтропия равномерного и гауссовского сообщений

Энтропия непрерывного сообщения зависит от закона распределе­ния сообщения, рассматриваемого с позиций случайного процесса. Будем считать сообщение стационарным случайным процессом, распре­деление которого определено одномерной плотностью вероятности р_x(x). Найдём энтропии сообщений с равномерным и гауссовским распределениями и сравним полученные результаты.

Энтропия сообщения с равномерным распределением равна

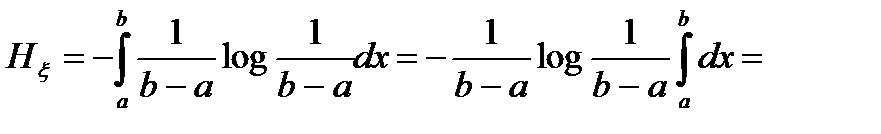
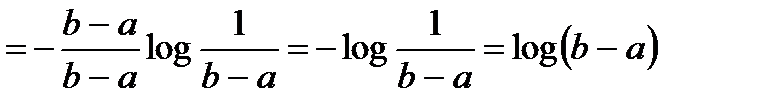, (2.12)

где использовалось, что .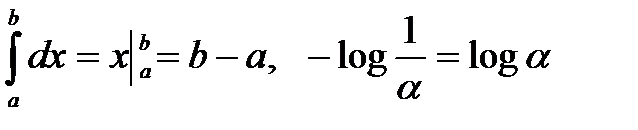

Из этого следует, что энтропия равномерного сообщения пол­ностью определяется логарифмом размаха уровня возможных значений сообщения. Пользуясь вариационным исчислением, можно показать, что равномерное распределение по сравнению с другими законами распределений, как и в случае дискретного сообщения, обладает наибольшей энтропией, если задан размах (b-а) как интервал сущес­твования случайной величины. При гауссовском распределении плотность вероятности равна

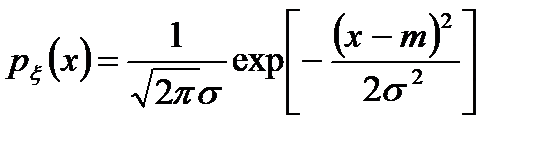. (2.13)

Логарифм от (2.13), в свою очередь, будет соответствовать вы­ражению

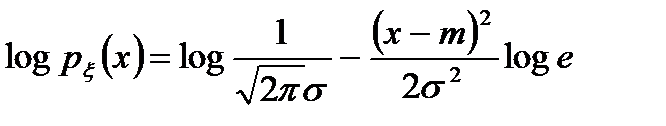. (2.14)

Энтропия гауссовского сообщения равна

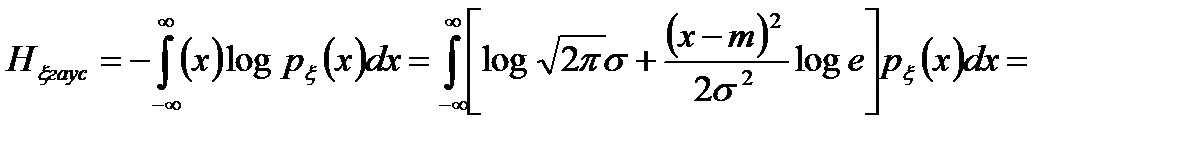
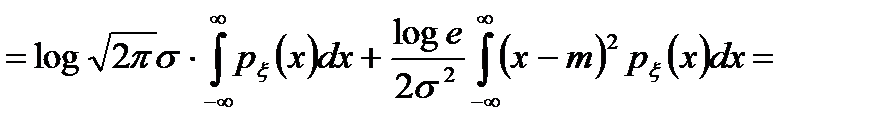
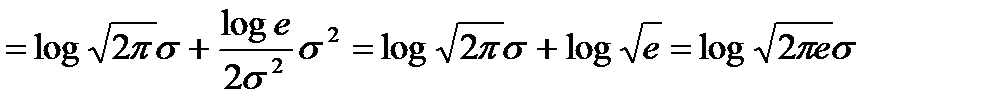, (2.15)

где при вычислении использовалось условие нормировки 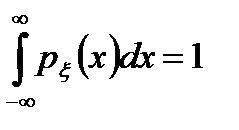и определение дисперсии: .

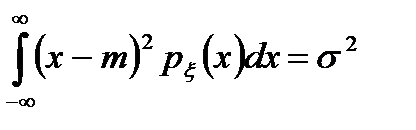Из этого следует, что энтропия гауссовского распределения зависит от среднего квадратического отклонения s. Этот результат соответствует физическому представлению, так как неопределённость случайной величины тем выше, чем больше степень разброса её возможных значений вокруг математического ожидания, то есть чем больше дисперсия s². Это значит, что рост s неизбежно приведет к увеличению энтропии, являющейся мерой неопределённости.

Полная удельная средняя мощность сообщения Р_cp с нормальным распределе­нием включает в себя мощность флюктуации s² и мощность постоянной составляющей m²;

Р_ср= s² ₊ m². (2.16)

Поэтому с целью экономии мощности всегда, где это возможно, выбирают для гауссовского сообщения нулевое математическое ожидание.

В этом случае

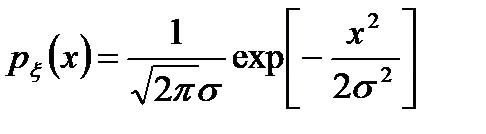, (2.17)

для которого формула (2.15) в полной мере справедлива.

Пользуясь вариационным исчислением, можно показать, что гауссовское распределение, по сравнению с другими законами распределения непрерывного сообщения, обладает наибольшей энтро­пией, если наложить условие постоянства дисперсий, что физически соответствует постоянству средней мощности сравниваемых сообщений. Этот результат можно объяснить тем фактом, что при нормальном распределении наиболее вероятные квантованные сообщения передаются на нулевом уровне мощности. Приведенный вывод можно подтвердить сравнением дисперсий равномерного и гауссовского сообщений, обладающих одинаковыми энтропиями.

Пусть H_xравн= Н_xгаус, тогда

;

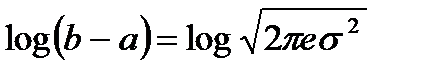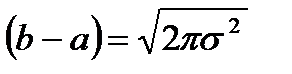; (2.18)

.

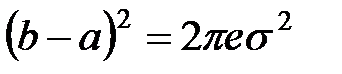Разделив обе части равенства на 12, получим

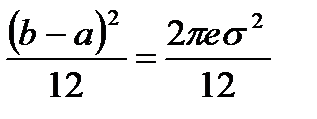. (2.19)

Учитывая, что левая часть равенства (2.19) соответствует дисперсии D_равн равномерного распределения, а дисперсией гауссовского распределения D_гаус является s², окончательно получим

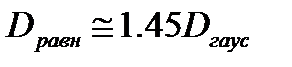(2.20)

Из этого следует, что для передачи одного и того же коли­чества информации непрерывному сообщению с равномерным распреде­лением потребуется затратить в 1,45 раз большую мощность, чем непрерывному сообщению с гауссовским распределением. Этот пример подтверждает, что гауссовское сообщение при заданной мощности обладает наибольшей информативностью, то есть при заданной мощно­сти гауссовское сообщение передаёт своим дискретом наибольшее количество информации.