Энтропия дискретного сообщения

В дискретной технике связи широко применяется алфавит из двух символов х₁ и х₂, которым приписываются значения "0" и "1". В этом случае слова, сообщения (или точнее кодовые комбинации) состоят из нескольких позиций. Чем больше число позиций в кодовой комбинации, тем больше будет число различных кодовых слов, но тем длиннее само слово.

Если позиция в кодовой комбинации одна, n=1, то можно образо­вать 2¹=2 слова: "0" и "1". Если позиций две, n =2, то можно обра­зовать четыре слова, 2² = 4: 00, 01, 10, 11. Если позиций три, n=3, то - 2³=8: 000, 001, 010, 011, 100, 101, 110, 111. В общем случае для двоичного кода число различных возможных кодовых комбинаций определяется формулой 2ⁿ, где m = 2 число символов в алфавите, или основание кода, an- число позиций в коде.

Рассмотрим энтропию двоичного кода. Поскольку имеется только два символа (m = 2), то энтропия, вычисленная по формуле (13.6), равна

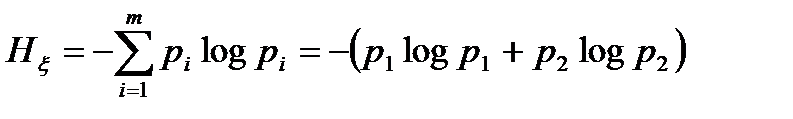. (1.12)

Так, в двоичном коде символы образуют полную группу несовмест­ных событий, для которых р₁ + р₂ = 1, р₂ = 1 - р₁. Для удобства анализа обозначим р₁ = р, р₂ = 1 - р. Тогда формула (1.12) при­мет вид

Н_x(р) = – [p log р + (1 – p) log(1 – p)]. (1.13)

Энтропию (1.13) будем рассматривать как функцию от вероят­ности одного из символов, р. График этой зависимости

Максимальное значение энтропии двоичного кода согласно (1.9) достигается при 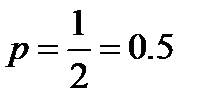, а сам максимум равен

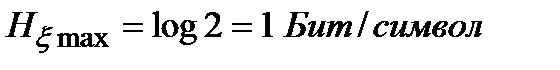. (1.14)

Энтропия обращается в нуль, при р = 0 или р = 1, что согласу­ется с (13.10) и следует непосредственно из симметричности (13.13) относительно р и (1-р).

Вернёмся к кодовой комбинации, содержащей n позиций. Если появление символов "0", "1" на любой позиции кода является равно­вероятным и независимым, то все комбинации будут равновероятны­ми, при этом вероятность появления любой комбинации (1/2)ⁿ = 2^-n. В этом случае каждая кодовая комбинация будет нести максимальную информацию, равную

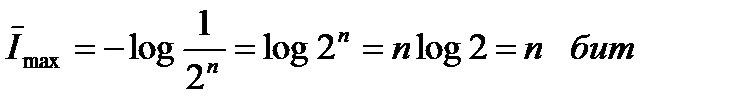. (1.15)

Результат (1.15) следует рассматривать следующим образом. В кодовой комбинации информация сообщения является суммой энтропий, определяемых для каждой позиции кода. Информация (1.15) равна n бит потому, что число позиций n, ив каждой позиции достигается максимальная энтропия, равная 1 бит/символ (1.14). Если же ве­роятность конкретного символа на той или иной позиции будет боль­ше или меньше 0,5 энтропия каждой позиции кода будет уменьшаться, что приведёт к уменьшению информации сообщения, которую следует записать в виде

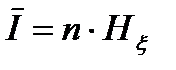, (1.16)

где Н_x- энтропия двоичного кода, определяемая формулой (1.13).