Вопрос. Цифровые фильтры. Системы дискретного времени.

Системы дискретного времени – систематические алгоритмы, на входе которых последовательность двоичных чисел x(t), а на выходе – последовательность двоичных чисел y(t).

Пример системы ДБ – цифровой фильтр.

Система дискретного времени может быть линейной и нелинейной, инвариантной относительно времени и изменятся во времени.

Система линейна, если она подчиняется принципу суперпозиции.

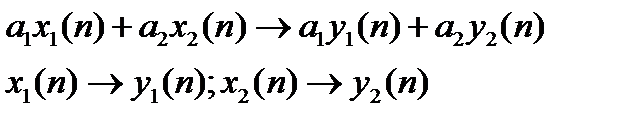
Система дискретного времени инвариантна относительно времени, если ее параметры не зависят от времени, то есть если вход x(t) дает выход y(t), то вход x(t)-k дает выход y(t)-k, то есть задержка входного сигнала приведет к такой задержке выходного. Взаимосвязь между входами и выходами линейной системы задается сверткой:

, где h(k) – импульсная характеристика.

Импульсная характеристика системы – отклик системы на единичный импульс. Значение единицы импульса 1 при n=0, u=0 при остальных n.

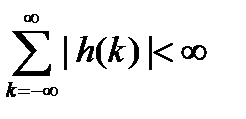
2 класса системы: 1) конечная импульсная характеристика (КИХ), то есть импульсная характеристика конечной длинны; 2) БИХ системы с импульсной характеристикой бесконечной длинны.

19 Вопрос. Z – преобразование.

Определяется следующим образом:

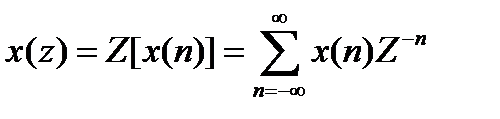, где z – комплексная переменная для системы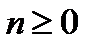

Z – преобразование – степенной ряд u имеет область сходимости, в которой x(z) – конечная.

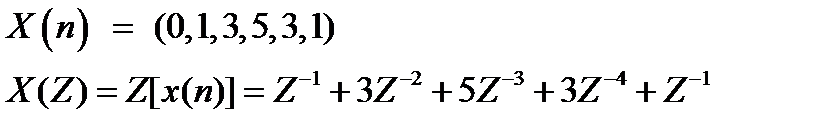
Обратное Z – преобразование позволяет восстановить последовательность по ее z – образу.

Z – образ можно разложить в степенной ряд:

Из данной записи видно, что коэффициенты можно найти как 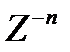. X(Z) выражается как отношение 2-х многочленов:

Обратное Z – преобразование может найти отличие 3-х методов: метода разложения в степенной ряд, метод разложения на элементарные дроби, метод вычетов.

Рассмотрим последний метод.

Свойства Z – преобразования:

1. Линейность – Z – преобразование от линейной комбинации 2-х последовательностей равна линейной комбинации Z – преобразования (линейная комбинация – a*x+b*y).

Z – преобразование от сигнала y(t) получена из исходного сигнала x(t) сдвигом на одну позицию в сторону запаздывания, равную Z – преобразованию исходного сигнала, домноженного на .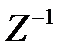

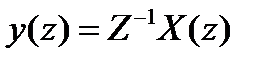, где 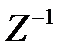- задержка на длину интервала дискретизации.

2. Дискретная свертка. Сверка двух дискретных сигналов соответствует произведению их Z – преобразований.