Вопрос. Быстрое преобразование Фурье.

Для вычисления ДПФ от сигнала из N – отсчетов необходимо провести 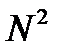операций с комплексными числами. Каждому из отсчетов сигнала ставится в соответствие элемент спектра, на вычисление которого необходимо N операций. Вычисление по такому алгоритму для больших массивов требует значительных затрат машинного времени.

БПФ (FFT) служит для преодоления этого недостатка.

Для вычисления БПФ требуется порядка 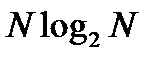операций, массив, содержащий 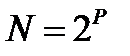отсчетов, Р – целое число. Если входной массив не укладывается в такую размерность, то его дополняют нулями. Если при вычислении ДПФ заменить вычисление одного ДПФ для массива из N элементов на вычисление 2х ДПФ для массива из N/2 элементов, объем увеличится в 2 раза.

Исходный массив разбивают до тех пор, пока не дойдут до массива из 2х элементов. Для такого массива вычисляют ДПФ по определению.

Чтобы перейти к исходной длине массива существуют алгоритмы объединения. Схемотехнически, данный алгоритм показан на рис. 38.

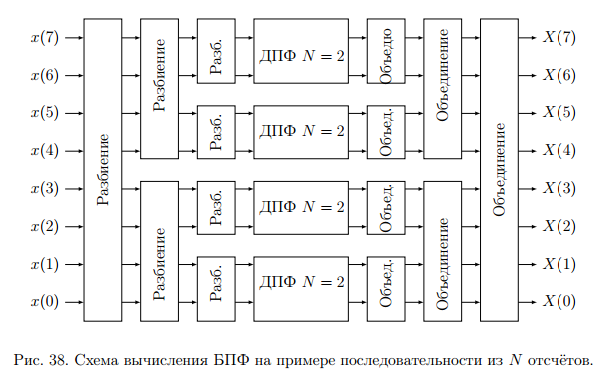
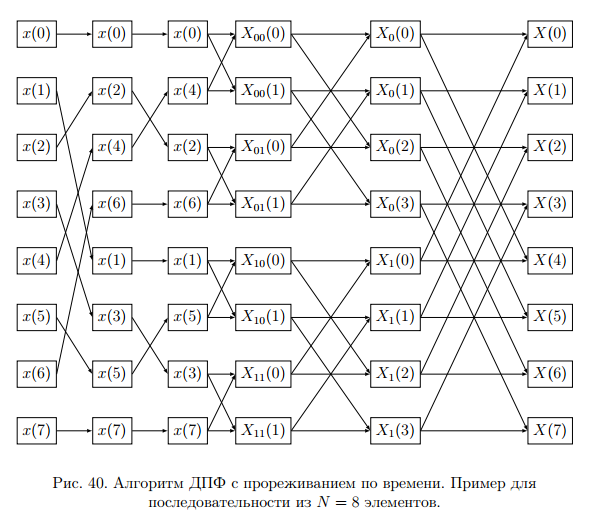
Одним из алгоритмов вычисления БПФ является алгоритм с прореживанием по времени. Структурная схема алгоритма с прореживанием по времени – рис.40.

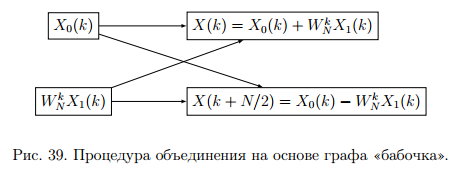
Операция объединения в данном алгоритме выполняется на основе поворотных коэффициентов. Процесс объединения схемотехнично показан на рис.39.

Подробное описание алгоритма смотри в методическом указании семинара №3.