Вопрос. Цифровые фильтры с конечной импульсной характеристикой (КИХ).

Физически осуществимые цифровые фильтры работают в реальном масштабе времени, для формирования выходного сигнала в i-ый дискретный момент времени могут использовать следующие данные:

1. Значения выходного сигнала в текущей момент времени; так же некоторое количество прошлых отсчетов входного сигнала: x(i-1), x(i-2), x(i-m);

2. Некоторое количество предыдущих отсчетов выходного сигнала: y(i-1), y(i-2), y(i-n).

Целые числа m и n определяют порядок цифрового фильтра. Фильтры классифицируются в зависимости от того, как используется информация о прошлом состоянии системы.

Фильтры с КИХ или не рекурсивные фильтры, работающие в соответствии со следующим алгоритмом.

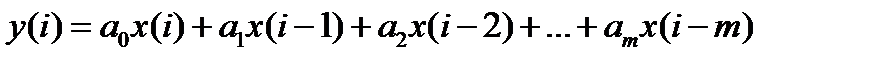, m – порядок фильтра.

Не рекурсивный фильтр производит взвешивание, суммирование предыдущих отсчётов входного сигнала. Прошлые отсчеты выходного сигнала не используются.

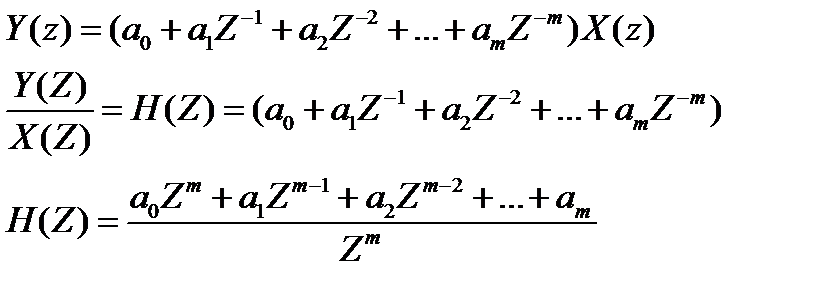
H(z) – системная функция.

Системная функция имеет m нулей и один полюс, при z=0.

Алгоритм функционирования цифрового фильтра с КИХ показан на рис.45.

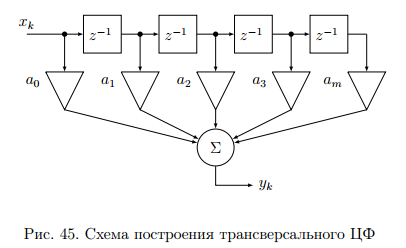
Основными элементами фильтра служат блоки задержки отсчетов значений на 1 интервал дискретизации .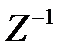

Масштабные блоки, выполняющие умножение на весовые коэффициенты в цифровой форме. С выхода масштабных блоков сигнал поступает в сумматор, где вычисляется выходной сигнал.

Данная структурная схема не является электрической, а служит графическим изображением алгоритма обработки сигнала на ЭВМ. Выходными и входными данными для такого алгоритма служат массивы чисел.

Применим к системным функциям обратное Z – преобразование и найдем импульсную характеристику:

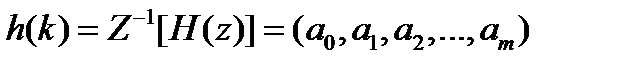(импульсная характеристика фильтра).

Импульсная характеристика КИХ фильтра содержит конечное число элементов и данный фильтр всегда устойчив.

Найдем частотную характеристику выполнив подстановку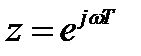

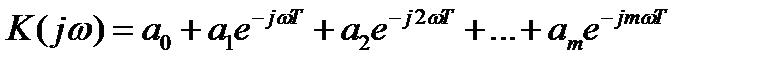
T=1/fs – интервал дискретизации.

Подбирая коэффициенты 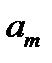в данном выражении можно получить АЧХ фильтра.

Пример программной реализации ЦФ с КИХ – семинар №4.