Вопрос. Дискретная свертка
Дискретной сверткой двух последовательностей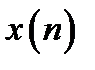 
и 
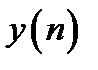называют последовательность 
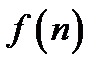, каждый элемент которой равен:
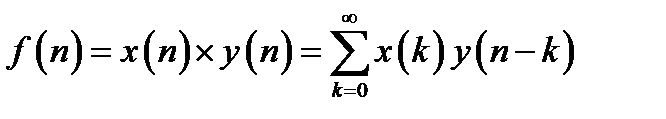
Дискретная свертка вводится по аналогии со сверткой двух аналоговых сигналов.
Различают линейную и круговую дискретные свертки. В случае круговой свертки предполагается, что дискретные сигналы периодические с одинаковым периодом N отсчетов.
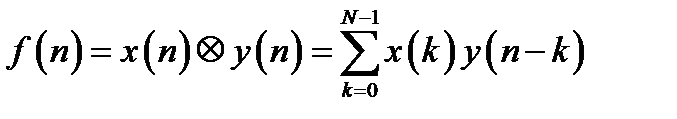
С помощью круговой свертки можно вычислить линейную свертку. Для этого нужно каждую из последовательностей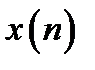 
длиной N отсчетов и 
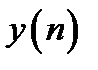длиной M отсчетов дополнить нулями до M=N-1 отсчетов.
Пример вычисления линейной свертки показан на (рис. 34).
На рисунке 34 утолщенной линией показана граница повторения периодических сигналов. На каждом шаге вычисляется круговая свертка, сигнал сдвигается циклически и последний отсчет заступает на место первого.
15 Вопрос. Свойства ДПФ:
1. Первый элемент ряда Фурье связан со средним значением, то есть постоянной составляющей сигнала:
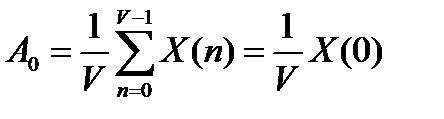
2. Симметрия. Амплитудный спектр симметричен, а фазовый ассиметричен.
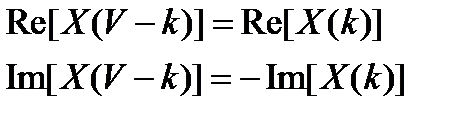
3. Теорема Парсевале
Теорема устанавливает равенство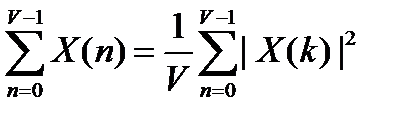 
4. 
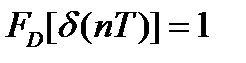
5. 
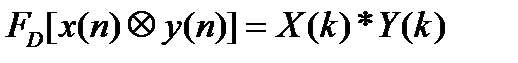
Операция свертки во временной области соответствует операции умножения в частотной области.
Пример смотри в методических указаниях к семинару №3.
Обратное ДПФ.
Обратное ДПФ позволяет перейти от частотной области во временную.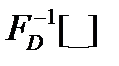 
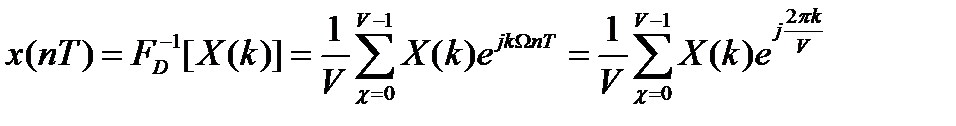
Обратное дискретное преобразование Фурье позволяет переходить от спектра к сигналу. При этом можно вычислить круговую свертку:
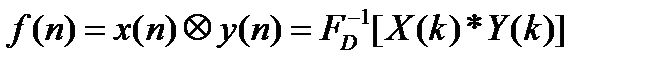
Дата добавления: 2015-12-29; просмотров: 6046;