Вопрос. Канонический рекурсивный фильтр.
Предназначен для оптимизации использования памяти рекурсивным алгоритмом фильтрации. Использует минимальное возможное число ячеек памяти (максимальное из числе m и n). Структурная схема фильтра показана на рис. 47.
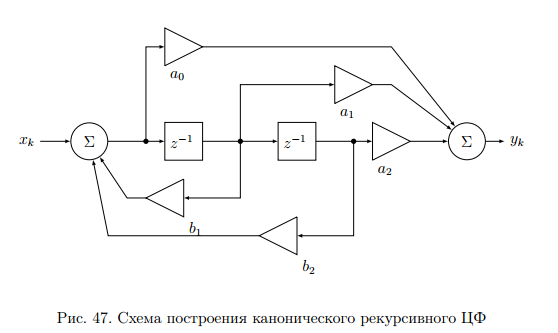
На рисунке изображен фильтр 2-ого порядка, системная функция которого равна:
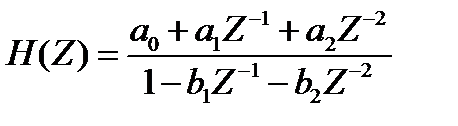
Вопрос. Синтез ЦФ. Метод инвариантных импульсных характеристик.
Задачей синтеза являются поиски значений коэффициентов a и b цифрового фильтра.
В основе данного метода лежит предположение, что синтезированный ЦФ должен обладать импульсной характеристикой, которая является результатом дискретизации соответствующей импульсной характеристики аналогового фильтра – прототипа.
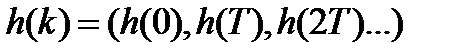
Число элементов импульсной характеристики может быть конечным или бесконечным. Это определяет структуру синтезируемых фильтров.
Связь между коэффициентами импульсной характеристики и структур фильтра наиболее проста для нерекурсивного фильтра. Синтез осуществляется путем применения z - преобразования к h(k).
Все приближения к АЧХ аналогового фильтра прототипа зависит от выбранного шага дискреции. При необходимости можно вычислить частотный коэффициент передачи и по нему АЧХ выполнив подстановку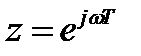 
.
Вопрос. Синтез ЦФ. Метод инвариантных частотных характеристик.
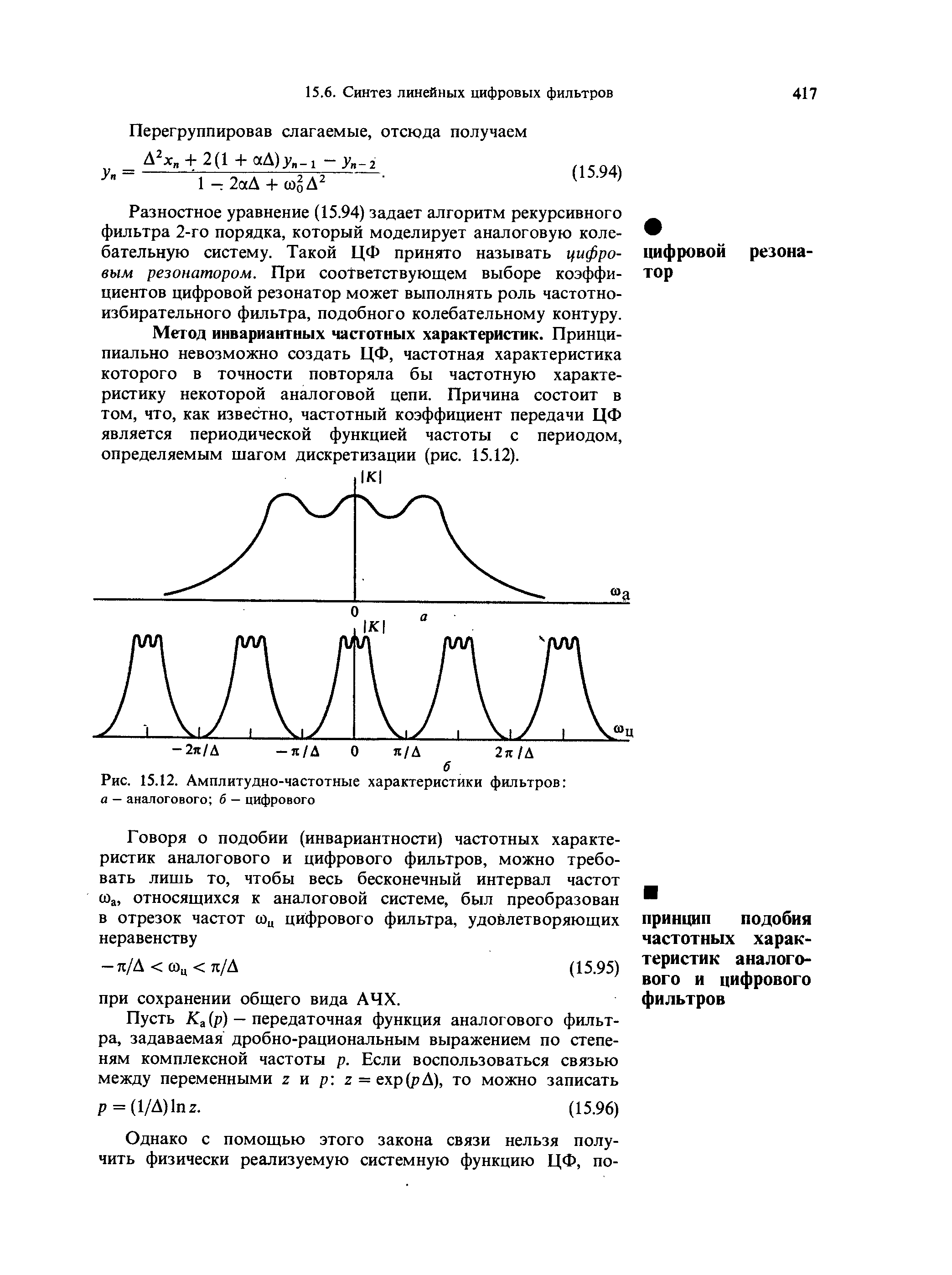
Принципиально невозможно создать ЦФ, частотная характеристика которого в точности повторяла бы частотную характеристику некоторой аналоговой цепи. Причина состоит в том, что частотный коэффициент передачи ЦФ является периодической функцией частоты с периодом, определяемым шагом дискретизации.
Подобие (инвариантность) частотных характеристик аналогового и цифрового фильтров, заключается в том, что весь бесконечный интервал частот wa аналоговой системы, был преобразован в отрезок частот wч ЦФ в интервале [-π/T; π/T] при сохранении общего вида АЧХ.
Билинейное Z – преобразование.
Билинейное Z – преобразование – это специальная установка, которая позволяет получить однозначное соответствие между точками в z – плоскости со всеми точками мнимой области в р – плоскости.
В справочниках: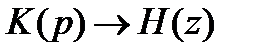 
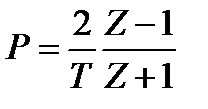- билинейное Z – преобразование.
В результате замены получается система функций цифрового фильтра.
Частоты аналоговой и цифровой системы связаны следующим соотношением:
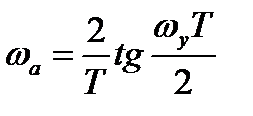
Если частота дискретизации достаточно велика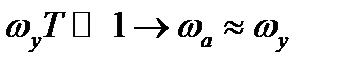 
, где Т = 1/fs – интервал дискретизации.
На низких частотах характеристики аналогового и цифрового фильтров практически совпадают.
Рассмотрим синтез фильтра
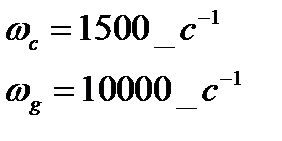частоты среза.
Определим шаг дискретизации: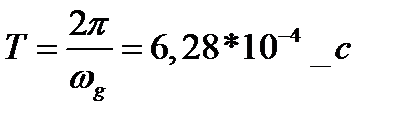 
Рассчитываем частоту среза фильтра – прототипа.
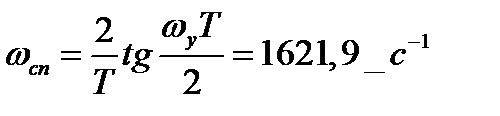
Находим передаточную функцию аналогового фильтра прототипа.
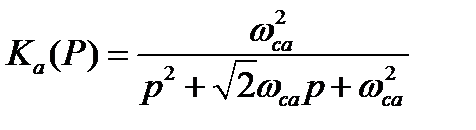
Выполним замену переменной p и находим систему функции цифрового фильтра.
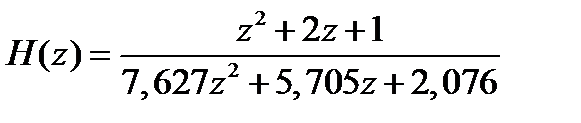
Дата добавления: 2015-12-29; просмотров: 1521;