Количественная мера информации. В теории информации количество информации, заключённое в со­общении, связывают с величиной неопределённости

В теории информации количество информации, заключённое в со­общении, связывают с величиной неопределённости, которая устраня­ется у получателя после того, как он это сообщение получит.

В простейшем случае для характеристики неопределенности како­го-либо события обычно используется вероятность этого события. Это означает, что для определения количества информации также используется вероятностная мера.

Пусть до получения сообщения получатель располагал априорной вероятностью Р₁ наступления интересующего его события. После по­лучения сообщений вероятность наступления этого события измени­лась и стала равной Р₂, при этом Р₂ > Р₁. Количество информации, которое в данном случае будет получено получателем, определим через логарифм отношения вероятностей:

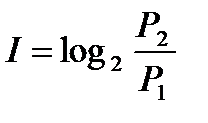(1.1)

Если с получением сообщения у получателя исчезла полностью имевшаяся ранее неопределённость, то Р =1 и

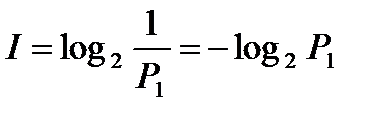(1.2)

В этом случае количество полученной информации определяется иск­лючительно той априорной вероятностью, которой располагал получа­тель до получения сообщений.

Если с получением сообщения неопределённость об интересующем событии у получателя не изменилась, то Р₂ = Р₁ и

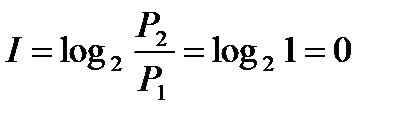
то есть получатель в этом случае никакой информации об этом собы­тии не получал.

Количество информации заключено в степени увеличения Р₂ по отношению к Р₁, в результате чего неопределённость уменьшается. Использование логарифма отношения в (1.1) обусловлено дополни­тельным требованием, чтобы информация о наступлении нескольких независимых событий, например и одного, и другого, представляемых в виде произведения этих событий, была бы равна сумме информации о каждом событии в отдельности. Этому требованию удовлетворяет логарифмическая функция, для которой log[P(A)Р(В)] = logP(A) + logP(B). Выбор основания логарифма с теоретической точки зрения является несущественным. Для практического использования оказа­лось удобным в формуле (1.1) выбрать логарифм при основании 2. Это обусловлено тем, что современные цифровые системы связи ис­пользуют двоичные коды, состоящие из двух элементов «0» и «1».

За единицу количества информации принимается такое её коли­чество, которое содержится в сообщении о том, что произошло одно из двух равновозможных событий. Это количество информации состав­ляет один «бит», сокращенное слово от английского "binary unit", что означает двоичная единица.

При определении количества информации в 1 бит имелось в виду, что Р₁=0.5, а Р₂ = 1. В этом случае согласно (1.1) имеем

,

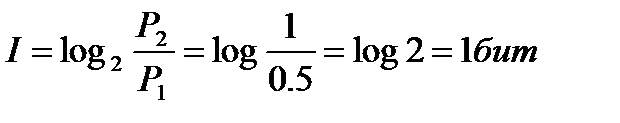где здесь и далее подразумевается, что основание логарифма равно двум. В дальнейшем основание 2 у логарифма писать не будем.