Дискретизация непрерывного сообщения

Сообщение называется непрерывным, если оно является непрерыв­ной функцией времени. В общем случае сообщение есть непрерывный случайный процесс, а конкретное сообщение реализация этого про­цесса. Представляет интерес определить собственное количество информации, заключённое в непрерывном сообщении, с тех же пози­ций, что и для дискретного сообщения, то есть с использованием понятия энтропии.

Замену непрерывной функции времени можно осуществить последо­вательностью дискретов на основании теоремы Котельникова, согласно которой если отсчёты непрерывного сообщения взять через интервал Dt=1/2F_c, где F_c - максимальная частота спектра реализации x(t), то непрерывная функция x(t) на интервале времени наблюдения [0,T] эквивалентна последовательности дискретных значений этой функции:

x(t) = [x(t)_, x(t₂), .... x(t_n)], (2.1)

где

n = T/Dt = 2F_cT. (2.2)

Замечаем, что число дискретов (2.2) непрерывного сообщения соответствует числу позиций в кодовой комбинации дискретного сообщения.

Теорема Котельникова позволяет заменить непрерывную функцию времени x(t) конечной последовательностью дискретов (2.1). Но при этом каждый дискрет x(t) в этой последовательности остается непрерывной величиной в том смысле, что он может занимать любое значение на числовой оси х. Однако в дискретном сообщении на любой позиции кода может находиться только один из возможных символов, составляющих алфавит из m символов, или в частном случае цифр. Поэтому в дискретной последовательности необходимо провести квантование по уровню.

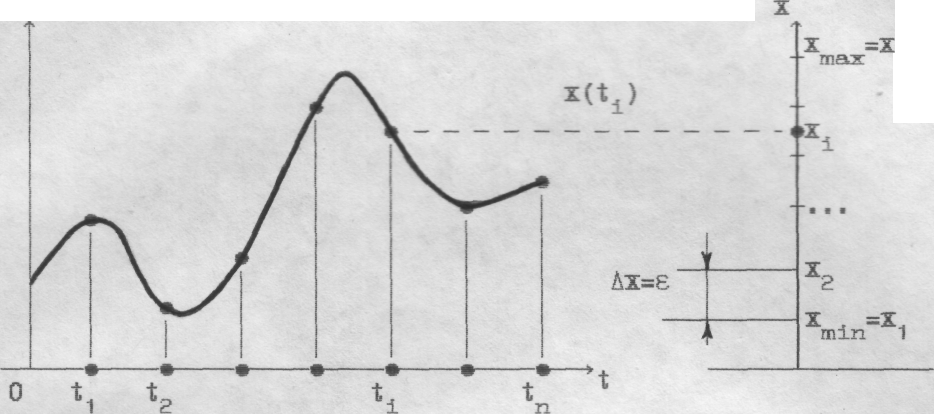
Для квантования по уровню выбирают шаг квантования Dх =e, находят наибольшее и наименьшее возможные значения сообщения x_max, x_min и определяют число уровней m:

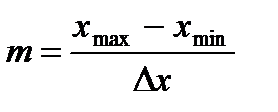. (2.3)

Во всем размахе возможных значений [x_max-x_min] определяют разрешённые уровни x₁,x₂,…,x_m. Процедура квантования в этом случае сводится к замене значения дискрета x(t_i), занимающего произвольную точку на оси х, на ближайший раз­решённый уровень (на рис. замена x(t_i) на x_i).

Число уровней m в этом случае будет эквивалентно числу симво­лов алфавита m дискретного сообщения. Таким образом, один кванто­ванный дискрет непрерывного сообщения может рассматриваться как один символ дискретного сообщения.