Дискретизация двумерной функции.

Все большую часть передаваемых по линии связи сообщений, составляют сигналы, являющиеся функциями не только времени - λ(t) (речь, музыка и т.п.), но и ряда других переменных, например, λ(x, y),λ(x, y, t) (статические и динамические изображения, карты физических полей и т.п.). В связи с этим естественным является вопрос: можно ли так, как это делается для временных сигналов (или других функций одной переменной), производить дискретизацию многомерных сигналов (функций нескольких переменных)?

Ответ на этот вопрос дает теорема дискретизации для двумерных (или в общем случае – для многомерных) сигналов, которая утверждает: функция двух переменных λ(x, y), двумерное преобразование Фурье которой

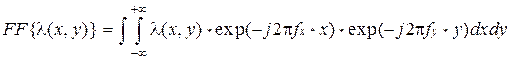(1.34)

равно нулю при f_x ≥ f_x max и f_y ≥ f_y max, однозначно определяется своими значениями в равноотстоящих точках плоскости переменных x и y, если интервал дискретизации удовлетворяет условию Δx ≤ 1/2f_x max, Δy ≤ 1/2f_y .Процедура дискретизации двумерной функции иллюстрируется примером, приведенным на рис. 1.13.

Доказательство двумерной теоремы дискретизации основано, так же как и для одномерного случая, на однозначном соответствии между сигналами и их спектрами: одинаковым изображениям (двумерным функциям) соответствуют одинаковые спектры, и наоборот, если спектры двух функций одинаковы, то и сами эти функции равны друг другу.

Преобразование Фурье (спектр) дискретизованной двумерной функции FF{λ(iDx, jDy)} получается периодическим продолжением спектра исходной непрерывной функции λ(x, y) в точки частотной плоскости (kDf_x , lDf_y) (рис. 1.14), где f_x и f_y – так называемые «пространственные частоты», являющиеся аналогами обычной «временной» частоты и отражающие скорость изменения двумерной функции λ (x, y)по соответствующим координатам (крупные фрагменты изображения – низкие частоты, мелкие детали – высокие частоты).

Аналитически это можно записать следующим образом:

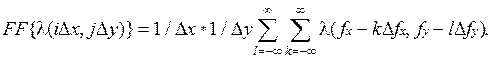(1.35)

Из рис. 1.8 видно, что если соблюдается условие неперекрываемости периодических продолжений спектра FF{λ(iDx, jDy)}, а это справедливо при Δx≤1/2f_xmax, Δy ≤ 1/2f_y max , то с помощью идеального двумерного ФНЧ с частотной характеристикой вида:

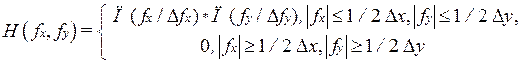(1.36)

из спектра дискретизованной функции FF{λ(iDx, jDy)} можно абсолютно точно выделить спектр исходной непрерывной функции FF{λ(x, y)} и, следовательно, восстановить саму функцию.

а

б

в

Рис. 1.13. Процедура дискретизации двухмерных изображение:
а - исходное изображение; б - дискретизация по осям x и y; в – дискретизированное изображение.

Таким образом, видно, что не существует принципиальных отличий в дискретизации между одномерными и двумерными (многомерными) функциями. Результатом дискретизации в обоих случаях является совокупность отсчетов функции, различия могут быть лишь в величине шага дискретизации, числе отсчетов и порядке их следования.

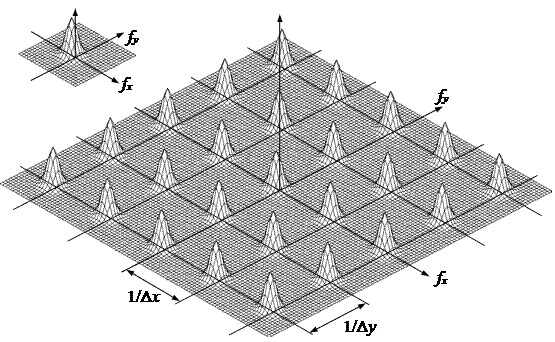
Рис. 1.14 Спектр дискретизированной двухмерной функции.

1.5.3. Квантование сообщений по уровню и по времени. Ошибки
квантования.

Итак, показано, что передачу практически любых сообщений λ(t)({λ(x, y)})можно свести к передаче их отсчетов, или чисел λ_i = λ(i Dt), следующих друг за другом с интервалом дискретности Dt £ 1/2F_m (Δx ≤ 1/2f_x , Δy ≤ 1/2f_y ). Тем самым непрерывное (бесконечное) множество возможных значений сообщения λ(t) заменяется конечным числом его дискретных значений {λ(i Dt)}. Однако сами эти числа имеют непрерывную шкалу уровней (значений), то есть принадлежат опять же континуальному множеству. Для абсолютно точного представления таких чисел, к примеру, в десятичной (или двоичной) форме, необходимо теоретически бесконечное число разрядов. Вместе с тем на практике нет необходимости в абсолютно точном представлении значений λ_i, как и любых чисел вообще.

Во-первых, сами источники сообщений обладают ограниченным динамическим диапазоном и вырабатывают исходные сообщения с определенным уровнем искажений и ошибок. Этот уровень может быть большим или меньшим, но абсолютной точности воспроизведения достичь невозможно.

Во-вторых, передача сообщений по каналам связи всегда производится в присутствии различного рода помех. Поэтому принятое (воспроизведенное) сообщение (оценка сообщения l^*(t) или L^*) всегда в определенной степени отличается от переданного, то есть на практике невозможна абсолютно точная передача сообщений при наличии помех в канале связи.

Наконец, сообщения передаются для их восприятия и использования получателем. Получатели же информации – органы чувств человека, исполнительные механизмы и т.д. – также обладают конечной разрешающей способностью, то есть не замечают незначительной разницы между абсолютно точным и приближенным значениями воспроизводимого сообщения. Порог чувствительности к искажениям также может быть различным, но он всегда есть.

С учетом этих замечаний процедуру дискретизации сообщений можно продолжить, а именно подвергнуть отсчеты λ_i квантованию.