Спектр одиночного прямоугольного импульса
Одиночный импульс можно рассматривать как непериодический сигнал, так как не существует конечного интервала времени T, отвечающего условию
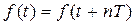 . (1.22)
. (1.22)
Наиболее просто и наглядно спектр непериодического сигнала можно получить из спектра периодического сигнала (1.16), принимая, что период T стремится к бесконечности, т.е. путем предельного перехода от ряда Фурье к интегралу Фурье
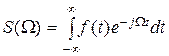 . (1.23)
. (1.23)
Величину S(W) называют спектральной функцией или просто спектральной плотностью.
Рассчитаем спектральную плотность одиночного прямоугольного импульса длительностью t (рис. 1.9).
Согласно (1.23)
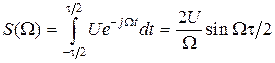 . (1.24)
. (1.24)
Последнее выражение может быть представлено в несколько ином виде:
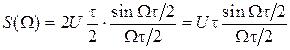 . (1.25)
. (1.25)
Здесь текущая частота W может принимать любые значения от нулевой до бесконечно большой (сплошной спектр). График для S(W) приведен на рис. 1.10.
 | |||
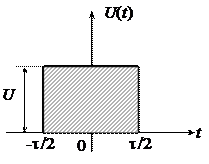 |
| Рис. 1.9. Прямоугольный импульс | Рис. 1.10. Спектр амплитуд прямоугольного импульса |
При частотах W = 2kp/t (k = 1, 2, 3,…) спектральная плотность S(W) = 0. Учитывая характер распределения S(W), можно отметить, что требуемая полоса частот вполне определяется спектром в пределах первого (k =1) нулевого значения спектральной плотности. При этом W = 2p /t = 2p..F, где F = 1/t. Таким образом, для непериодического сигнала необходимая полоса частот может быть найдена из уравнения
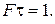 (1.26)
(1.26)
Данный вывод вытекает и из того, что энергия непериодического сигнала пропорциональна интегралу от квадрата спектральной плотности
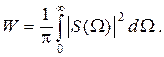 (1.27)
(1.27)
Если спектр сигнала ограничивается частотой Wmax, то энергия уменьшается до значения
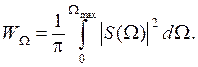 (1.28)
(1.28)
Зависимость энергии WW от наибольшей частоты ограничения Wmax спектра прямоугольного импульса показана на рис. 1.11.
Из рис. 1.10 и 1.11 следует, что наибольшее энергетическое значение имеют составляющие низкочастотной части спектра импульса. С ростом ширины сохраняемой части спектра от нуля до величины Wmax= 2p/t энергия WW быстро увеличивается и достигает 90 % всей энергии W. При дальнейшем увеличении спектра энергия WW нарастает все медленнее. Таким образом, при ширине спектра Wmax= 2p/t или F=1/t обеспечивается передача значительной части энергии сигнала. Чем короче импульс, тем более широкий спектр должен быть сохранен.

Рис. 1.11. Зависимость энергии импульса от ширины сохраняемой части спектра
Итак, мы рассмотрели как сообщения (первичные сигналы), с которыми приходится иметь дело в телемеханике, так и переносчики, с помощью которых они передаются. Прежде чем переходить к изучению методов образования сигналов, остановимся на некоторых вопросах преобразования непрерывных сообщений в дискретные. Такое преобразование имеет место в цифровых телеизмерительных системах, в системах связи при передаче речи, музыки, телевизионных изображениях и т.п.
Дата добавления: 2016-02-04; просмотров: 6798;
