Квантование по времени (дискретизация).

Непрерывные сообщения представляют собой непрерывные функции времени с бесконечным числом промежуточных точек. Для передачи таких сообщений без погрешности необходим канал связи с бесконечной пропускной способностью. На практике всегда передача сообщений осуществляется с ограниченными спектром частот и точностью, так как все каналы имеют ограниченную пропускную способность.

Если непрерывное сообщение имеет ограниченный спектр частот, оно всегда может быть передано своими значениями в отдельные моменты времени, т.е. может быть превращено в дискретное во времени сообщение, состоящее из последовательного во времени ряда значений.

Возможность такой замены была впервые установлена и сформулирована в 1933 г. В. А. Котельниковым в виде следующей теоремы: «Если функция f(t) не содержит частот выше F_max Гц, то она полностью определяется своими мгновенными значениями в моменты времени, отстоящие друг от друга на 1/2F_max», т. е.

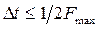. (1.29)

Функцию с ограниченным спектром можно записать в виде тригонометрического ряда

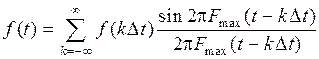, (1.30)

где k – порядковый номер отсчета функции.

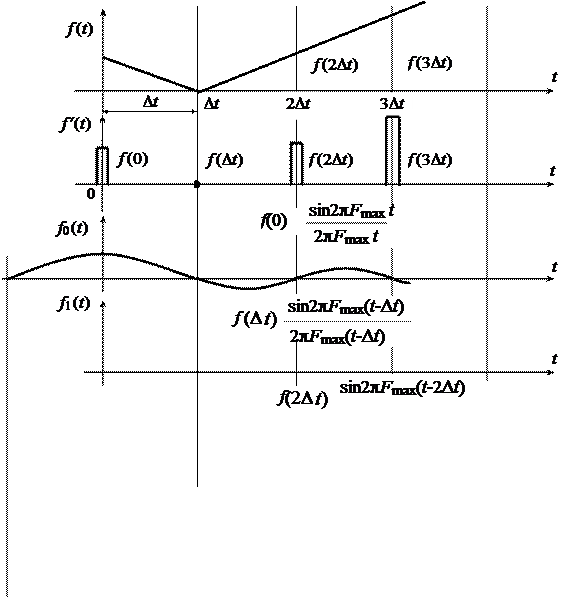
При этом функция вполне определяется своими мгновенными значениями f(kDt), отсчитанными через равные интервалы времени Dt, называемые интервалами дискретизации (рис. 1.12).

Свойства ряда (1.30) основываются на свойстве функции (sin x)/x, равной 1 при x=0 и равной 0 при x, кратных p (180, 360, 540° и т.д.).

Физический смысл преобразования состоит в том, что каждый член ряда (1.30) представляет собой отклик идеального фильтра нижних частот с граничной частотой среза F_max на очень короткий импульс, возникающий в момент времени kDt (рис. 1.12) и имеющий площадь, равную мгновенному значению функции f(t).

Интересным свойством ряда (1.30) является то, что значения ряда в момент kDt определяются только k-м членом ряда, так как все другие члены в этот момент времени обращаются в нуль:

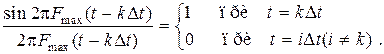(1.31)

Следовательно, несмотря на то, что выходные функции перекрываются, значением заданной функции в момент отсчета является только одно из ее значений.

Согласно теореме Котельникова для однозначного представления функции с ограниченным спектром на интервале времени T достаточно иметь N значений этой функции, т.е.

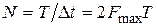. (1.32)

Аналогичные результаты можно получить для функций со спектром частот в промежутке от F₁ до F₂.

Таким образом, непрерывное сообщение сводится к сигналу в виде последовательности импульсов, амплитуда которых равна значению исходной функции, передаваемой в дискретные моменты времени kDt, а интервалы между ними Dt = 1/2F_max.

При выполнении условий (1.29) непрерывная и дискретная во времени функции обратимы между собой (тождественны).

Для преобразования дискретной функции в непрерывную нужно включить идеальный фильтр частот с частотой среза равной F_max.

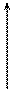
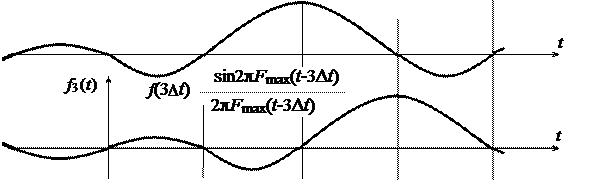Рис. 1.12. Разложение функции f(t) с ограниченным спектром

частот по В.А.Котельникову

Рассмотренный процесс преобразования непрерывного сообщения в дискретный во времени сигнал называется дискретизацией во времени.

В заключение следует отметить, что при определении на практике интервала дискретизации теорему Котельникова можно применять с поправкой

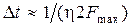, (1.33)

где h – коэффициент, зависящий от точности воспроизведения функции и способа интерполяции; при линейной интерполяции 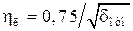, при ступенчатой 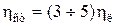(относительная погрешность воспроизведения).