КОЛИЧЕСТВЕННАЯ ОЦЕНКА ИНФОРМАЦИИ

2.1. Количество информации при равновероятности состояний
источника сообщений

Сообщения разнятся как по своей природе, так и по содержанию и по назначению. В связи с этим возникают трудности в оценке количества информации, которое содержится в сообщениях. Количество информации должно определяться через нечто общее, объективно присущее всему многообразию различной информации, оставаясь при этом созвучным нашим интуитивным представлениям, связанным с фактом получения информации. Этим общим, характеризующим фактом получения произвольной информации, является, во-первых, наличие опыта. Всякая информация добывается нами в результате опыта и только опыта. Во-вторых, до опыта должна существовать некоторая неопределенность в том или ином исходе опыта.

Таким образом, до опыта всегда имеется большая или меньшая неопределенность в интересующей нас ситуации. После опыта ситуация становится более определенной и на поставленный вопрос мы можем ответить либо однозначно, либо число возможных ответов уменьшится и, следовательно, уменьшится существовавшая ранее неопределенность. Количество уменьшенной неопределенности после опыта, очевидно, можно отождествить с количеством получаемой информации в результате опыта.

Теперь ясно, что для установления формулы для вычисления количества информации необходимо уметь вычислять неопределенность некоторой ситуации до и после опыта. Разность между этими количествами неопределенности и дает нам искомое количество информации, полученное от такого опыта.

К количеству информации (неопределенности до опыта) можно предъявить три интуитивных требования.

1. Количество получаемой информации больше в том опыте, у которого большее число возможных исходов.

Обозначая количество информации буквой I, а число возможных исходов n, первый постулат запишем в виде:

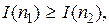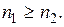если (2.1)

2. Опыт с единственным исходом несет количество информации, равное нулю, т.е.

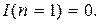(2.2)

3. Количество информации от двух независимых опытов равно сумме количества информации от каждого из них:

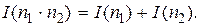(2.3)

Очевидно, единственной функцией аргумента n, удовлетворяющей трем поставленным условиям, является логарифмическая. Итак, количество информации от опыта с N исходами при условии, что после опыта неопределенность отсутствует:

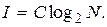(2.4)

Выбор постоянной С и основания логарифмов здесь несущественен, так как определяет только масштаб на единицу неопределенности. Поэтому положим С = 1, а = 2. Тогда

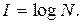(2.5)

Указанная мера была предложена Р. Хартли в 1928г. для количественной оценки способности системы хранить или передавать информацию.

Такая мера удовлетворяет требованию аддитивности. Емкость устройства состоящего из n ячеек, имеющего N = mⁿ состояний, равна емкости одной ячейки, умноженной на число ячеек:

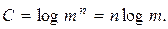(2.6)

За единицу измерения емкости принята двоичная единица или bit, равная емкости одной ячейки с двумя возможными состояниями.

Следует отметить, что мера количества информации в виде (2.6) относится к весьма частному случаю, когда после опыта неопределенности в исходе нет и все исходы равновероятны.

Дальнейшее развитие теории информации шло в направлении учета статистических характеристик.

Если от источника информации по каналу связи передавать сообщение о событии, априорная вероятность которого на передающей стороне равна Р₁, то после приема сообщения апостериорная вероятность этого события для приемника информации равна Р₂ и количество информации, полученное в результате приема сообщения, будет

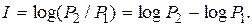(2.7)

Для канала связи без помех и искажений прием сообщения становится достоверным событием, т.е. вероятность Р₂ = 1, тогда из (2.7) следует, что

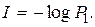(2.8)

Из (2.8) следует, что чем меньше вероятность Р₁, тем больше неопределенность исхода, т.е. тем большее количество информации содержится в принятом сообщении.

Значение Р₁ находится в пределах 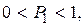следовательно, 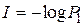всегда положительная величина.

Количество информации 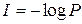, где Р – вероятность события, было положено в основу и было исходной точкой создания теории информации.

Энтропия ансамбля

Ансамблем называется полная совокупность состояний с вероятностями их появлений, составляющими в сумме единицу:

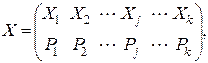(2.9)

причем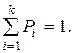

Пусть имеет место N возможных исходов опыта, из них k разных, и i-й исход (i = 1, 2,..., k) повторяется n_i раз и вносит информацию, количество которой оценивается как I_i . Тогда средняя информация, доставляемая одним опытом, равна

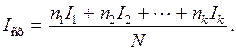(2.10)

Но количество информации в каждом исходе согласно (2.8) будет

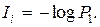(2.11)

Тогда

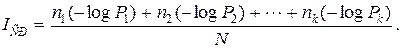(2.12)

Но отношение 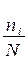представляют собой частоты повторения исходов, а следовательно, могут быть заменены их вероятностями:

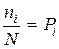. (2.13)

Подставляя (2.13) в (2.12), получим

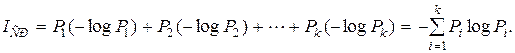
Полученную величину К. Шеннон назвал энтропией и обозначил буквой Н, бит:

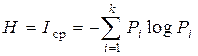. (2.14)

Энтропия Н представляет собой логарифмическую меру беспорядочности состояния источника сообщений и характеризует степень неопределенности состояния этого источника. Получение информации – это процесс раскрытия неопределенности.

В информационных системах неопределенность снижается за счёт принятой информации, поэтому численно энтропия Н равна среднему количеству информации, несомой произвольным исходом x_i, т.е. является количественной мерой информации.

Если все k различных состояний источника равновероятны, то

,

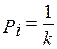энтропия максимальна и из (2.14) имеем

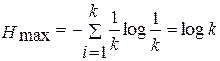. (2.15)

Нетрудно заметить, что в частном случае при равновероятных сообщениях формулы (2.14) и (2.5) совпадают. Совпадение оценок количества информации по Шеннону и Хартли свидетельствуют о полном использовании информационной емкости системы. В случае неравных вероятностей количество информации по Шеннону меньше информационной емкости системы.