Энтропия объединения
Объединением называется совокупность двух и более взаимозависимых ансамблей дискретных случайных переменных.
Рассмотрим объединение, состоящее из двух ансамблей X и Y, например из двух дискретных измеряемых величин, связанных между собой вероятностными зависимостями. Объединение ансамблей характеризуется матрицей P(X, Y) вероятностей P(xi, yi) всех возможных комбинаций состояний 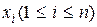 ансамбля X и состояний
ансамбля X и состояний 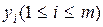 ансамбля Y:
ансамбля Y:
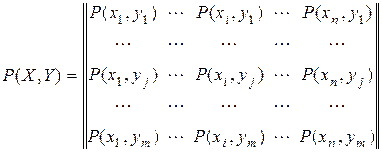 . (2.16)
. (2.16)
Cуммируя столбцы и строки матрицы (2.16), получим  информацию об ансамблях X и Y исходных источников:
информацию об ансамблях X и Y исходных источников:
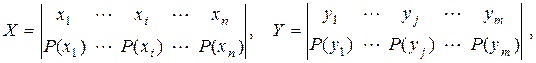 (2.17)
(2.17)
где 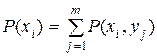 и
и 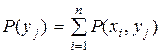 .
.
Вероятности P(xi, yj) совместной реализации взаимозависимых состояний xi и yi можно выразить через условные вероятности P(xi /yj) или P(yj /xi) в соответствии с тем, какие состояния принять за причину, а какие – за следствие.
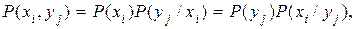 (2.18)
(2.18)
где P(xi /yj) – вероятность реализации состояний xi ансамбля X при условии, что реализовалось состояние yj ансамбля Y; P(yj / xi) – вероятность реализации состояний yj ансамбля Y при условии, что реализовалось состояние xi ансамбля X.
Тогда выражение для энтропии объединения в соответствии с (2.14) принимает вид:
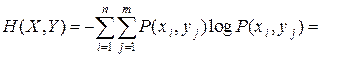
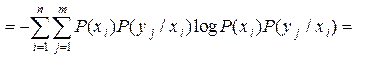
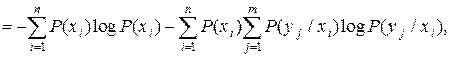 (2.19)
(2.19)
где 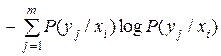 – случайная величина, характеризующая неопределенность, приходящуюся на одно состояние ансамбля Y при условии, что реализовалось конкретное состояние xi ансамбля X . Назовем её частной условной энтропией ансамбля Y и обозначим H(Y/xi):
– случайная величина, характеризующая неопределенность, приходящуюся на одно состояние ансамбля Y при условии, что реализовалось конкретное состояние xi ансамбля X . Назовем её частной условной энтропией ансамбля Y и обозначим H(Y/xi):
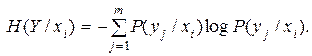 (2.20)
(2.20)
При усреднении по всем состояниям ансамбля X получаем среднюю неопределенность, приходящуюся на одно состояние ансамбля Y при известных состояниях ансамбля X:
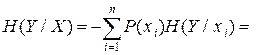
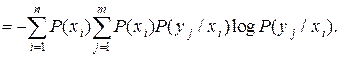 (2.21)
(2.21)
Величину H(Y/X) называют полной условной или просто условной энтропией ансамбля Y по отношению к ансамблю X.
Подставляя (2.21) в (2.19), получаем
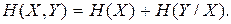 (2.22)
(2.22)
Выражая 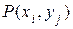 через другую условную вероятность в соответствии с (1.18), найдем
через другую условную вероятность в соответствии с (1.18), найдем
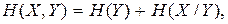 (2.23)
(2.23)
где
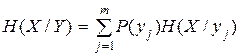 (2.24)
(2.24)
и 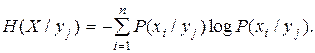 (2.25)
(2.25)
Таким образом, энтропия объединения двух статистически связанных ансамблей X и Y равна безусловной энтропии одного ансамбля плюс условная энтропия другого относительно первого.
В случае статистической независимости ансамблей X и Y имеют
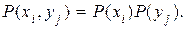
Тогда
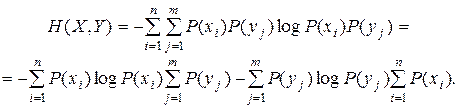
Учитывая, что
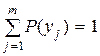 и
и 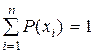 ,
,
получим
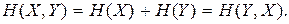 (2.26)
(2.26)
Свойства энтропии
2.4.1. Энтропия всегда неотрицательна, так как значения вероятностей выражаются дробными величинами, а их логарифмы – отрицательными величинами (2.14).
2.4.2. Энтропия равна нулю в том крайнем случае, когда одно событие равно единице, а все остальные – нулю. Это положение соответствует случаю, когда состояние источника полностью определено.
2.4.3. Энтропия имеет наибольшее значение при условии, когда все вероятности равны между собой (2.15).
2.4.4. Энтропия источника Х с двумя состояниями х1 и х2 изменяется от нуля до единицы, достигая максимума при равенстве их вероятностей
Р(х1) = Р = Р(х2) = 1 - Р = 0,5.
График зависимости Н(Х) в функции Р:
Н(Х) =-[PlogP + (1-P)log(1-P)], (2.27)
приведен на рис. 2.1.
Отметим, что энтропия непрерывно зависит от вероятности отдельных состояний, что непосредственно вытекает из непрерывности функции -PlogP.
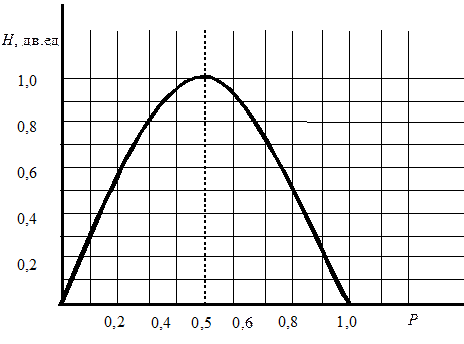
Рис. 2.1. Зависимость Н(Х) в функции Р
2.4.5. Энтропия объединения нескольких статистически независимых источников информации равна сумме энтропий исходных источников
H(X,Y,Z,..., W) = H(X) + H(Y) + H(Z) + ... + H(W). (2.28)
2.4.6. Энтропия объединения двух статистически связанных ансамблей X и Y равна
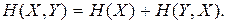
2.4.7. Энтропия объединения любого числа зависимых ансамблей определяется из выражения
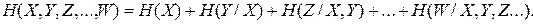 (2.29)
(2.29)
2.4.8. Энтропия не зависит от значений, принимаемых случайными величинами, а зависит только от вероятностей их появления (2.14).
2.4.9. Если события xi и yj статистически независимы при любых i и j, то
H(Y/X) = H(Y) и H(X/Y) = H(X). (2.30)
Таким образом, сведения о результатах выбора состояний из одного ансамбля не снижает неопределенности выбора состояний из другого ансамбля. Если имеет место однозначная связь в реализациях состояний 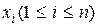 из ансамбля X и
из ансамбля X и 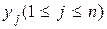 из ансамбля Y, то условная энтропия любого из ансамблей равна нулю:
из ансамбля Y, то условная энтропия любого из ансамблей равна нулю:
H(Y/X) = 0, H(X/Y) = 0. (2.31)
Действительно, условные вероятности P(xi/yj) и P(yj, xi) в этом случае принимают значения, равные нулю или единице. Поэтому все слагаемые, входящие в выражения (2.20) и (2.25), для частных условных энтропий равны нулю. Тогда в соответствии с (2.21) и (2.24) условные энтропии равны нулю.
Равенства (2.31) отражают факт отсутствия дополнительной неопределенности при выборе событий из второго ансамбля.
Уяснению соотношений между рассмотренными энтропиями дискретных источников информации (ансамблей) соответствует их графическое отображение (рис. 2.2).
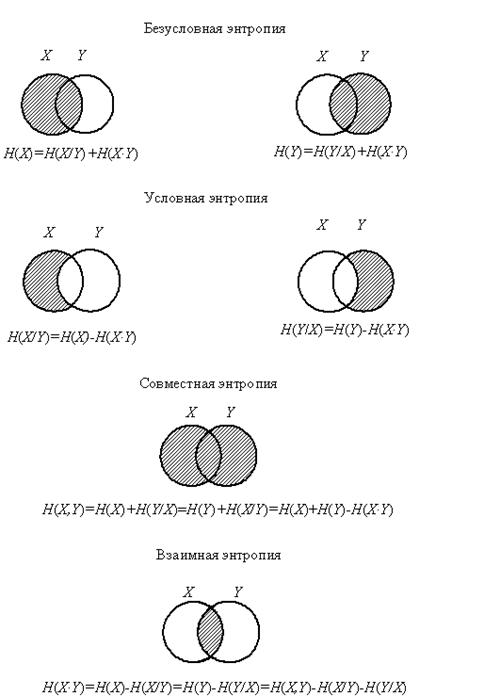
Рис. 2.2. Энтропия объединения
Дата добавления: 2016-02-04; просмотров: 5915;
