Энтропия эргодического источника

Достаточно хорошей математической моделью дискретных источников, встречающихся на практике, являются так называемые эргодические источники. Назовём эргодическим источником r-го порядка такой источник, у которого вероятность появления некоторого символа x_j зависит от r предыдущих. Для такого источника может быть найдено конечное число характерных состояний S₁, S₂,..., таких, что условная вероятность появления очередного символа зависит лишь от того, в каком из этих состояний находится источник. Вырабатывая очередной символ, источник переходит из одного состояния в другое либо возвращается в исходное состояние.

Определим энтропию эргодического источника в предположении, что он работает длительное время и, всякий раз, когда мы ждём появления очередного символа, нам известно, какие символы были выбраны ранее, и, следовательно, известно, в каком характерном состоянии находится источник.

Обозначим через P(S_i) вероятность того, что источник находится в состоянии S_i, причём

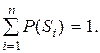(3.1)

Предположим, мы установили, что источник находится в состоянии S_b. У нас имеется неопределённость, из какого состояния S_k источник, выработав некоторый символ, перешёл в состояние S_b. Так как вероятность состояния S_b зависит только от предыдущего состояния S_k и не зависит от того, в каких состояниях находился источник ранее, неопределённость источника в состоянии S_k можно найти по формуле, аналогичной (2.14):

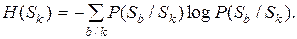(3.2)

Величина H(S_k) случайно меняется в зависимости от состояния источника, поэтому только среднее значение H(S_k) может характеризовать энтропию источника:

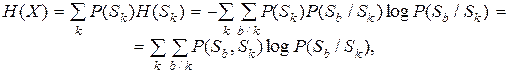
где значок b/k у суммы означает, что производится суммирование по всем переходам из состояния S_k в S_b.

Таким образом, энтропия Н(Х) есть среднее значение (математическое ожидание) энтропий всех характерных состояний источника.

В случае, когда символы источника независимы, имеется лишь одно состояние S₁, вероятность которого P(S₁) = 1. При появлении символа x_i источник вновь возвращается в состояние S₁ (рис. 3.1), и при этом P(S₁/S₁) = P(x_i), следовательно,

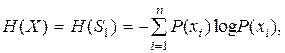
что совпадает с (2.14).

Если коррелятивные связи имеются между двумя соседними символами, то P(S_k) = P(x_k) и P(S_b/S_k) = P(x_b/x_k).

Из (3.3) тогда получим

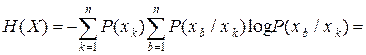
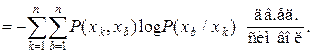(3.4)

Источник, генерирующий n разных символов – x₁, x₂, ... , x_n, в этом случае может иметь n характерных состояний. Пример такого источника для случая n = 3 приведён на рис. 3.2.

В случае когда коррелятивные связи имеются между тремя символами, характерные состояния определяются передачей двух символов, и их удобно нумеровать двумя индексами. Так, если генерируются x_h x_j, то источник переходит в состояние S_hj и тогда:

P(S_hj) = P(x_h,x_j) и P(S_ji/S_hj) = P(x_i/x_h,x_j) .

Из (3.4) получаем

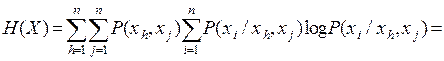
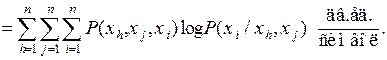(3.5)

Чисел характерных состояний для этого случая столько, сколько имеется различных пар (x_i,x_h). Таких пар, очевидно, n² .

Аналогичные соотношения получаются и в случае, когда коррелятивные связи распространяются на большее число символов.