Основные свойства количества информации

2.6.1. I(X,Y) = I(Y,X), т.е. количество информации, содержащееся в случайном объекте Y о случайном объекте Х, равно количеству информации, содержащемуся в случайном объекте Х о случайном объекте Y. Свойство 2.6.1 сразу же следует из (2.37), если учесть, что P(x_i, y_j) = P(y_j, x_i) .

2.6.2. 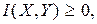причём знак равенства имеет место, когда объекты X и Y независимы.

Положительность I(X,Y) следует из свойства энтропии : если события x_i и y_j статистически зависимы, то всегда H(Y/X) < H(Y) и H(X/Y) < H(X).

2.6.3. I(X,Y) = H(X), т.е. энтропия может быть истолкована как информация, содержащаяся в объектах относительно самих себя. Из этого также непосредственно вытекает, что энтропия есть максимальное количество информации, которое можно получить об объекте. Это возможно при взаимно однозначном соответствии между множествами передаваемых и принимаемых сообщений, что имеет место в отсутствии помехи, апостериорная энтропия равна нулю и количество информации численно совпадает с энтропией источника.

Контрольные вопросы

1. В чём сущность требования аддитивности к мере неопределённости выбора?

2. Назовите основной недостаток меры неопределённости, предложенной Р. Хартли.

3. Укажите достоинства и недостатки способа, предложенного К. Шенноном.

4. Что необходимо учитывать при выборе способа измерения количества информации?

5. В каких единицах измеряется количество информации?

6. Дайте определение энтропии.

7. Назовите основные свойства энтропии дискретного ансамбля.

8. Почему вводится понятие условной энтропии? Запишите выражение для условной энтропии и поясните её смысл.

9. Приведите выражение для энтропии двух взаимосвязанных ансамблей.

10. Как связаны между собой понятия количества информации и энтропии?

11. В чём различаются понятия частного и среднего количества информации?

12. Когда энтропия источника с двумя состояниями достигает максимума?

13. От чего не зависит энтропия случайного процесса?

14. Запишите выражение для энтропии объединения нескольких независимых источников информации.

15. Перечислите свойства количества информации.