Количество информации от опыта в общем случае

Передача информации инициируется либо самим источником информации, либо осуществляется по запросу. На приемной стороне любой системы передачи информации до получения сигнала от интересующего нас источника неизвестно, какой из возможных сигналов будет передан, но считается известным распределение вероятностей Р(x_i) по всем сигналам. Неопределенность ситуации до приема сигнала характеризуется энтропией:

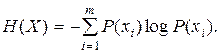(2.32)

Далее в приемное устройство поступает принятый сигнал. Поскольку предполагается, что принятый сигнал соответствует переданному (помехи отсутствуют), то неопределенность относительно источника информации снимается полностью.

Таким образом, в результате приема сигнала, с одной стороны, произошло уменьшение неопределенности с Н(Х) до нуля, а с другой стороны, получено количество информации I, численно равное энтропии Н(Х). Отсюда следует, что количество информации может быть определено как мера снятой неопределенности. Численное значение количества информации о некотором объекте равно разности энтропий объекта до и после приема сигнала. Значит, понятие энтропия является первичным, исходным, а понятие количество информации – вторичным, производным понятием. Энтропия есть мера неопределенности, а количество информации – мера изменения неопределенности.

Если помехи существуют, то принятый сигнал в той или иной степени не тождественен переданному. Здесь исчезает численное совпадение I и H. Количество информации будет меньше, чем при отсутствии помех, так как прием сигнала не уменьшает энтропию до нуля.

Рассмотрим случай, когда между элементами сообщения и помехой статистические связи отсутствуют, искажения отдельных элементов сообщения являются событиями независимыми и адресату известна совокупность условных вероятностей 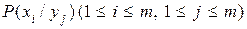того, что вместо элемента сообщения x_i будет принят элемент сообщения y_j._.

Среднее количество неопределенности, которым мы обладали до опыта, равнялось Н(Х). Представим теперь что мы приняли какой-то сигнал y_j и оцениваем, какова неопределенность (после опыта) соответствия его некоторому переданному x_i. Эта неопределенность равна

H(x_i / y_j) = -logP(x_i / y_j). (2.33)

Как видим, неопределенность этого соответствия является случайной величиной, значения которой при каждом заданном y_j наступают с вероятностями P(x_i/y_j). Поэтому среднее значение количества неопределенности соответствия данного y_j любому из x_i равно

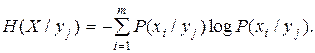(2.34)

Величина H(X/y_j) также случайна. Вероятности её значений равны P(y_j). Тогда среднее значение H(X/y_j) определит среднее количество неопределённости соответствия любого y_j любому из x_i. Обозначим это среднее H(X/Y):

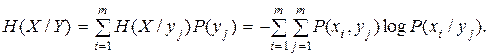(2.35)

Другими словами, H(X/Y) есть средняя неопределённость в передаче того или иного x_i, если известно, что принят тот или иной y_j, или, кратко, средняя неопределённость ансамбля X после опыта.

Таким образом, мы установили, что неопределённость передачи некоторого сигнала Х до опыта Н(Х), а после опыта H(X/Y). Поэтому количество информации, имеющееся в Y o X:

I(Y,X) = H(X) – H(X/Y). (2.36)

Эта мера количества информации получена нами на примере передачи сообщений по каналу связи. Совершенно аналогичные рассуждения могут быть применены к случайным объектам произвольного вида и приведут нас к той же мере.

Подставим в выражение (2.36) необходимые значения H(X) и H(X/Y) из (2.32) и (2.35) соответственно получим

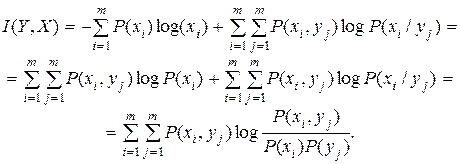
Если частный характер количества информации специально не оговаривается, мы всегда имеем дело с количеством информации, приходящимся в среднем на один элемент сообщения. Поэтому указание об усреднении опускаются.