Свойство энтропии эргодических источников

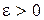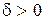Теорема 1.Для любых и можно найти такое M₀, при котором эргодические последовательности с длиной 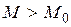распадаются на два класса:

1) типичные, вероятности которых удовлетворяют следующему неравенству:

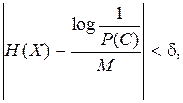(3.6)

где Н(Х) – энтропия эргодического источника;

2) нетипичные, сумма вероятностей которых меньше e.

Доказательство.Последовательность C длины M образуется в результате поочередного перехода источника из одного характерного состояния в другое.

Рассмотрим переход из состояния S_k в состояние S_b во множестве последовательностей С. Число M всегда может быть выбрано настолько большим, что сумма вероятностей всех нетипичных последовательностей меньше e. Учитывая, что для типичной последовательности частота событий может быть как угодно близка к их вероятности, можно утверждать, что в каждой типичной последовательности источник пребывает в состоянии S_k приблизительно M_p(S_k) раз, а число переходов из состояния S_k в состояние S_b приблизительно равно M_p(S_k) P(S_b/S_k), а точнее

M(P(S_k) P(S_b /S_k) ± h), (3.7)

где h с увеличением M может быть сделано как угодно малым.

Вероятность того, что в рассматриваемой последовательности имеет место М переходов из состояния S_k в S_b, равна по теореме умножения вероятностей

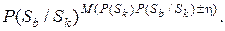(3.8)

Вероятность появления конкретной последовательности С определяется как вероятность всех возможных переходов, и, следовательно,

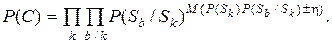(3.9)

Логарифмируя последнее равенство, получаем:

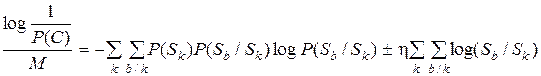.(3.10)

Если учесть, что первая сумма в правой части совпадает с (3.3), а вторая вследствие произвольной малости h всегда может быть меньше d, то получим неопределённость (3.6).

Рис. 2.2. Диаграмма перехода, когда источник имеет три характерных состояния

Следствие 1. Типичные последовательности приблизительно равновероятны. Для доказательства из (3.6) найдём Р(С):

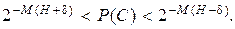
При 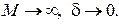Поэтому при достаточно большом М можно положить

P(C) » 2^-MH(X). (3.11)

Из (2.11) видно, что все последовательности С равновероятны и число их

N_T = 2^MH(X). (3.12)

В случае, если все n символов источника независимы и равновероятны, то

N_T = 2^Mlogn = n^M. (3.13)

Легко видеть, что (3.13) определяет число всех возможных последовательностей длины М, содержащих n различных символов.

Следствие 2. Чтобы экспериментально определить энтропию эргодического источника, у которого вероятностные связи распространяются на очень большое число символов, нам необходимо располагать последовательностью ещё большей длины ( 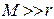); при этом вычисленная энтропия будет как угодно близка к своему пределу log1/P(C) = H(X).