Свойства дифференциальной энтропии

1. Величина 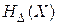изменяется при изменении масштаба измерения Х.

Изменим масштаб случайной величины Х в k раз, оставив неизменным масштаб равномерно распределенной в единичном интервале случайной величины Х₀, принятой за эталон. Если x_i = kx, то 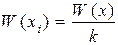. Тогда

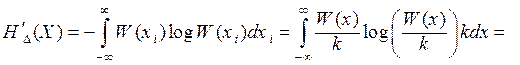
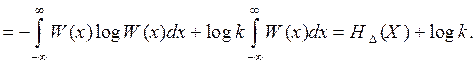(4.7)

Если одновременно изменить масштаб Х₀, соотносительная неопределенность также изменится, так как значение эталона будет уже иным.

Из относительности дифференциальной энтропии следует, что энтропия может принимать положительные, отрицательные и нулевые значения.

2. Дифференциальная энтропия не зависит от конкретных значений случайной величины Х и, в частности, от изменения всех еe значений на постоянное. Действительно, масштаб Х при этом не меняется и справедливо равенство

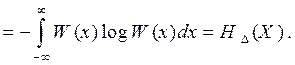(4.8)

3. Если единственным ограничением для случайной величины Х является область её возможных значений [a, b], то максимальной дифференциальной энтропией обладает равномерное распределение вероятностей в этой области, т.е. при W(X) = (b - a)^-1:

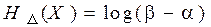. (4.9)

4. Если ограничения на область значений непрерывной случайной величины Х отсутствуют, но известно, что дисперсия её ограничена, то максимальной дифференциальной энтропией, равной

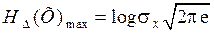, (4.10)

обладает нормальное (Гауссовское) распределение величин Х:

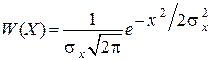. (4.11)

5. Соотношения для дифференциальной энтропии объединения статистически зависимых непрерывных источников аналогичны соответствующим формулам для дискретных источников:

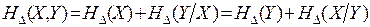, (4.12)

где .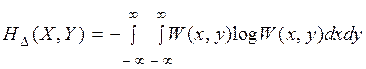

6. Если статистические связи между X и Y отсутствуют, то

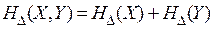. (4.13)