Эпсилон - энтропия источника сообщений

Реальная чувствительность приемных устройств, органов чувств человека и разрешающая способность различных информационно-измерительных систем ограничены. Поэтому воспроизводить непрерывные сообщения абсолютно точно не требуется. Наличие помех и искажений сигналов в реальных каналах делает точное воспроизведение сообщений невозможным. Поэтому введём понятие эпсилон–энтропии. Эпсилон–энтропия – это то среднее количество информации в одном независимом отсчете непрерывного случайного процесса Х(t), которое необходимо для воспроизведения этого сигнала с заданной среднеквадратичной погрешностью e_о .

Рассмотрим подробнее сущность этого понятия. Предположим, что передавался сигнал Х(t), а был принят сигнал Y(t). Пусть в канале действует аддитивная помеха E(t), тогда Y(t) = X(t) + E(t) . Расстояние между сигналами X(t) и Y(t) определяется величиной

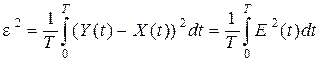, (4.14)

где T – длительность сигналов.

Если 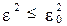, то сигналы называют 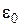– близкими.

В соответствии с определением эпсилон-энтропии можно записать, что

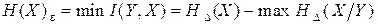. (4.15)

Так как 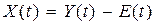, то условная энтропия 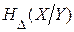при принятом Y(t) полностью определяется “шумом” воспроизведения E(t). Поэтому

max H_D(X/Y) = max H_D(E). (4.16)

Учитываем, что мощность помехи ограничена величиной e₀², тогда максимальная энтропия помехи, отнесенная к одному отсчету, определяется по формуле (4.10)

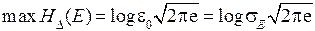, (4.17)

где s_Е – среднеквадратическое значение помехи.

С учетом (4.17)

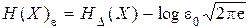. (4.18)

Эпсилон-энтропия имеет максимальное значение, когда процесс X(t) также является гауссовским:

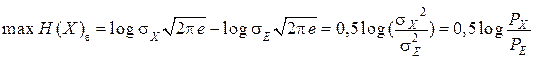. (4.19)

Отношение сигнал/шум s_Х²/s_E² = P_X/P_E характеризует то количество полученной информации, при котором принятый сигнал Y(t) и переданный сигнал X(t) «похожи» в среднеквадратичном смысле с точностью до e₀² = s_Е². В формуле (4.19) значение эпсилон-энтропии определено для одного независимого отсчета.