ГЛАВА 6 ЛИНЕЙНЫЕ ЦЕПИ С НЕСИНУСОДАЛЬНЫМИ ИСТОЧНИКАМИ
Основные понятия и определения
В главе 3 мы рассмотрели процессы в цепях переменного тока при гармонических изменениях Э.Д.С. и токов. На практике мы часто встречаемся с несинусоидальными периодическими Э.Д.С. и токами, которые изменяются во времени не по гармоническому закону, но значения которых регулярно повторяются при истечении полного цикла изменений Т, как это показано на рис. 6.1.
 Несинусоидальное Э.Д.С. и токи возникают при включении в цепь переменного тока элемента с насыщенным стальным сердечником, наличие нелинейных сопротивлений в цепи, включение некоторых преобразователей энергии и в ряде других случаев.
Несинусоидальное Э.Д.С. и токи возникают при включении в цепь переменного тока элемента с насыщенным стальным сердечником, наличие нелинейных сопротивлений в цепи, включение некоторых преобразователей энергии и в ряде других случаев.
Обычным приёмом является представление несинусоидальных Э.Д.С. или токов в виде суммы синусоидальных Э.Д.С. и токов при помощи разложения в ряд Фурье.
Для периодичной несинусоидальной Э.Д.С. можем записать:
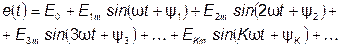 , (6.1)
, (6.1)
где 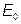 - постоянная составляющая Э.Д.С.;
- постоянная составляющая Э.Д.С.;
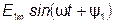 - основная или первая гармоника;
- основная или первая гармоника;
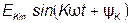 - высшая гармоника порядка k;
- высшая гармоника порядка k;
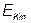 - амплитуда;
- амплитуда;
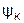 - начальная фаза k-й гармоники.
- начальная фаза k-й гармоники.
Заметим, что разложение в ряд Фурье возможно для функций, удовлетворяющим условиям Дирихле, то есть имеющих за полный период конечное число разрывов первого рода и конечное число максимумов и минимумов. Этим условия всегда удовлетворяют Э.Д.С., напряжения и токи в реальных физических цепях.
Для вычисления коэффициентов ряда Фурье целесообразно его члены представить через синусы и косинусы без начальных фаз. Имеем:
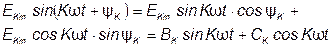 . (6.2)
. (6.2)
Таким образом,
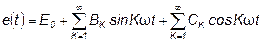 . (6.3)
. (6.3)
Из курса математики известны формулы для нахождения 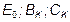 :
:
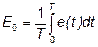 ; (6.4)
; (6.4)
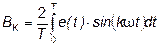 ; (6.5)
; (6.5)
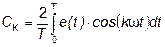 . (6.6)
. (6.6)
Имея 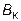 и
и 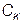 , находим амплитуду и начальную фазу:
, находим амплитуду и начальную фазу:
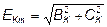 ; (6.7)
; (6.7)
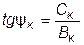 . (6.8)
. (6.8)
В общем случае ряд Фурье содержит бесконечное число членов, но, как правило, обычно можно ограничиться некоторым конечным числом члена ряда (обычно 3-4).
Таким образом, несинусоидальный источник напряжения можно представить упрощенно как схему, изображенную на (рис. 6.2)

Значительное число непериодических функций времени, с которыми приходится встречаться в электротехнике (рис. 6.3), удовлетворяет условию:

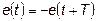 . (6.9)
. (6.9)
Функции, удовлетворяющие этому условию, называются симметричными относительно оси абсцисс. Они раскладываются в ряд, который не содержит четных гармоник и постоянной составляющей:
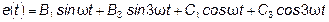 . (6.10)
. (6.10)
В схемах выпрямления переменного тока часто приходится встречаться с функциями, которые при соответствующем выборе начала координат удовлетворяют условию.
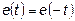 . (6.11)
. (6.11)
Такие функции называются симметричными относительно оси ординат (рис. 6.4).
В этом случае ряд не содержит синусов:
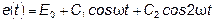 . (6.12)
. (6.12)

В схемах умножения частоты встречаются функции, которые при выборе начала координат в точке нуля функции удовлетворяют условию (рис. 6.5).
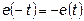 . (6.13)
. (6.13)

Такие функции называются симметричными относительно начала координат. Они раскладываются в ряд, не содержащий косинусов о постоянной составляющей:
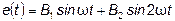 . (6.14)
. (6.14)
При оценке несинусоидальных периодических кривых в электроэнергетике используются коэффициент формы 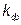 , коэффициент амплитуды
, коэффициент амплитуды 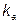 , коэффициент искажения
, коэффициент искажения 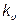 .
.
Коэффициент формы определяется как отношение действующего значения к среднему по модулю значению:
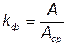 . (6.15)
. (6.15)
Для синусоиды 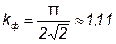 .
.
Коэффициент амплитуды равен отношению максимального значения к действующему значению:
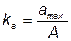 . (6.16)
. (6.16)
Для синусоиды 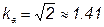 .
.
Коэффициент искажения определяется как отношение действующего значения основной (первой) гармоники к действующему значению все кривой:
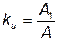 . (6.17)
. (6.17)
Для синусоиды 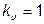 .
.
Представим в виде ряда выражение для мгновенной Э.Д.С., действующей в цепи:
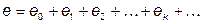 (6.18)
(6.18)
и, определяя действующую Э.Д.С. по известному выражению
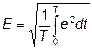 , (6.19)
, (6.19)
в результате получим:
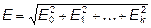 , где
, где 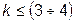 . (6.20)
. (6.20)
Подобно выражению 6.20 получим выражение для действующего тока:
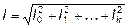 , где
, где 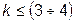 .
.
Дата добавления: 2016-02-02; просмотров: 949;
