Соединение четырехполюсников
Четырёхполюсники соединяются различными способами. Чаще всего встречаются следующие виды соединений четырёхполюсников:
1. 
Последовательно – последовательное (или просто последовательное) соединение, при котором последовательно соединены и входные и выходные зажимы четырёхполюсников.
Существуют схемы, в которых входные зажимы четырёхполюсников соединены последовательно, а выходные - параллельно. В этом случае соединение называется последовательно – параллельным. Схема такого соединения представлена на рис. 7.5 напряжение на входе (выходе) эквивалентного четырёхполюсника равно сумме напряжений на входе (выходе) составляющих его четырёхполюсников, а токи соответственно на входе (выходе) последовательно соединённых четырёхполюсников одинаковые.
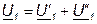

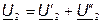
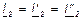
Для анализа последовательно соединённых четырёхполюсников применяют формулу записи Z (или Z-матрицу):
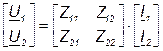
Эквивалентная Z-матрица в этом случае равна сумме Z- матриц первого и второго четырёхполюсников, то есть:
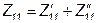
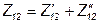
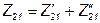
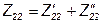
2. 
Параллельное (или параллельно - параллельное) соединение, при котором и входные и выходные зажимы четырёхполюсников соединены параллельно (рис. 7.6).
В этом случае ток на входе (выходе) эквивалентного четырёхполюсника равен сумме токов на входе (выходе) составляющих четырёхполюсников:
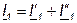
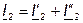
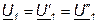

Для анализа параллельно соединённых четырёхполюсников используют Y - форму (или Y - матрицу):
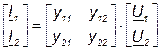
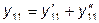

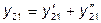
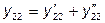
3. Каскадное соединение, при котором входные выводы одного четырёхполюсника соединяются с выходными выводами другого (рис. 7.7). В общем случае каскадное соединение может состоять из n – четырёхполюсников.

Если в каскад соединяются несколько одинаковых четырёхполюсников, то каскадное соединение называется однородной цепной схемой (или проще - однородной цепочкой).
Такой цепочкой может быть заменена, например, линия передачи электроэнергии (Л.Э.П.).
Каждый четырёхполюсник, входящий в цепочку, называется её звеном.
Для описания работы четырёхполюсников, соединённых в каскад, применяется форма А (или А-матрица). При этом эквивалентная А–матрица будет равна произведению А–матриц первого и второго четырёхполюсников:
 или
или 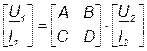
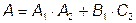
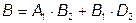
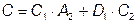
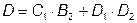
4. Соединение четырёхполюсников с обратной связью в электротехнике принято называть воздействие выходной величины устройства на вход этого же устройства.
В системах управления обратная связь используется для сравнения входного сигнала с заданным входным значением и выполнения соответствующей коррекции последнего.
Схема четырёхполюсника с обратной связью приведена на рис. 7.8.
 |
Здесь Н(р) – передаточная функция (как было сказано выше, четырёхполюсник по сути является передаточным звеном).
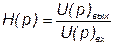 . (7.19)
. (7.19)
В системах автоматического управления передаточную функцию Н(р) (по старому обозначению W(p)) принято выражать через оператор Лапласа р.
На вход четырёхполюсника с передаточной функцией Н(р) поступают напряжение 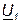 (входной сигнал) и напряжение обратной связи
(входной сигнал) и напряжение обратной связи 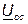 через четырёхполюсник обратной связи с передаточной функцией К. В зависимости от характера взаимодействия сигнала
через четырёхполюсник обратной связи с передаточной функцией К. В зависимости от характера взаимодействия сигнала 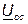 на входной сигнал
на входной сигнал 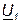 различают отрицательную и положительную обратные связи.
различают отрицательную и положительную обратные связи.
В схеме с отрицательной обратной связью входной сигнал частично ослабляется сигналом обратной связи.
При положительной обратной связи, наоборот, происходит некоторое усиление входного сигнала под действием напряжения обратной связи.
Поэтому входной сигнал :
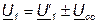
где «+» - если обратная связь отрицательная;
«-» - если обратная связь положительная.
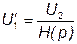

При отрицательной обратной связи сигнал на входе равен:
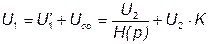
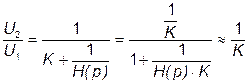 ; (7.20)
; (7.20)
7.6 Анализ четырёхполюсников с помощью вторичных параметров (  )
)
Напомним, что вторичными параметрами четырёхполюсника являются характеристическое сопротивление 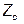 и постоянная передачи
и постоянная передачи 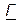 .
.
В случаях, когда исследуемый пассивный четырёхполюсник является симметричным, бывает целесообразным воспользоваться уравнениями, в которых токи и напряжения связаны между собой при помощи вторичных параметров.
Для составления таких уравнений выразим коэффициенты матрицы А (A , B, C, D) через вторичные параметры.
Было записано, что
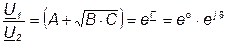
тогда 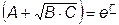
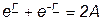
откуда 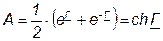 . (7.21)
. (7.21)
Если записать 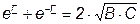 , то
, то
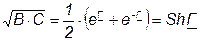
Так как 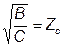 , умножив обе части этого равенства на
, умножив обе части этого равенства на 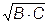 , запишем:
, запишем:
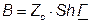 . (7.22)
. (7.22)
Если обе части равенства  умножить на
умножить на  , то получим:
, то получим:
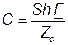 . (7.23)
. (7.23)
Так как четырёхполюсник симметричный, то
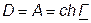 . (7.24)
. (7.24)
Подставив найденные коэффициенты в систему уравнений 7.1 запишем А – форму через вторичные параметры:
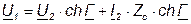 ; (7.25)
; (7.25)
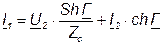 . (7.26)
. (7.26)
Дата добавления: 2016-02-02; просмотров: 1025;
