Диагональное соединение горных выработок и его свойства
Диагональным называется соединение выработок, при котором две параллельные выработки соединяются между собой, кроме начального и конечного пунктов, еще одной или несколькими дополнительными выработками называемыми диагоналями. А под диагональю понимается такая ветвь-выработка, направление движения воздуха в которой может измениться на противоположное при изменении аэродинамического сопротитивления других ветвей.
Диагональное соединение бывают простые и сложные. Диагональное соединение с одной диагональю называется простым (рис.5.12), двумя и более сложным (рис.5.13).
 |
При обычном ведении горных работ аэродинамическое сопротивление выработок, может изменяеться до величин в 15-20 раз от первоначального, а при авариях изменения могут быть более значительными. Поэтому в диагоналях может происходить самопроизвольное опрокидывание вентиляционной струи, что не только не желательно, но и может быть причиной аварии.
Относительно просто аналитическими методами рассчитывается лишь простое диагональное соединение.
Расчет простого диагонального соединения
Известны сопротивления ветвей простого диагонально соединения R1, R2, R3,
 |
R4, R5, а также общее количество воздуха проходящего через это соединение Q или общая депрессия соединения Н. Необходимо определить количество воздуха во всех ветвях соединения q1, q2, q3, q4, q5 и общее сопротивление соединения R0
Для решения поставленной задачи, прежде всего, необходимо определить направление движения воздуха в диагонали 2, 3. В зависимости от величины давления в узлах 2, 3.воздух в диагонали может двигаться в любую сторону или не двигаться совсем. Так если принять, что давление в узлах 2, 3 одинаково то воздух в диагонали не пойдет.
Р2=Р3 q5=0 (5.35)
Выразим давление в узлах 2, 3 через давление в узлах 1, 4 и депрессию.
Р2=Р1-h1-2 (5.36)
Р3=Р1-h1-3 (5.37)
Р2=Р4 +h2-4 (5.38)
Р3=Р4-h3-4 (5.39)
Подставляя значения давления из равенств (5.36, 5.39) в равенство (5.35) получим
h1-2=h1-3 (5.40)
h2-4=h3-4 (5.41)
Выразим депрессии в равенствах (5.40), (5.41) через аэродинамические сопротивления ветвей и потоки воздуха
R1 q 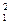 =R2 q
=R2 q 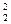 (5.42)
(5.42)
R3 q 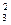 =R4 q
=R4 q 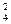 (5.43)
(5.43)
Так как воздух в диагонали не идет q5=0 то q1=q3, а q2=q4 тогда разделив равенство (5.42) на равенство (5.43) получим
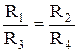 (5.44)
(5.44)
Равенство (5.44) является условием того, что воздух в диагонали не пойдет.
Допустим, что воздух в диагонали движется от узла 2 к узлу 3. Это условие будет выполняться, если давление в узле 2 будет больше чем давление в узле 3.
Р2>Р3 (5.45)
Подставляя значения давлений их равенств (5.37, 5.39) в равенство (5.45) получим
h1-2<h1-3 (5.46)
h2-4>h3-4 (5.47)
Выразим депрессии в неравенствах (5.46) (5.47) через аэродинамические сопротивления ветвей им потоки воздуха предварительно имея в виду, что Q=q2+q3+q5; q1=q3+q5; q4=q2+q5.
ТогдаR1*(q3+q5)2<R2*q 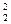 (5.48)
(5.48)
R3*q 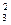 >R4*(q2+q5)2 (5.49)
>R4*(q2+q5)2 (5.49)
Разделив неравенство (5.48) на неравенство (5.49) получим
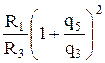 <
< 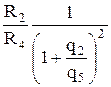 (5.50)
(5.50)
Выражения в скобках неравенства (4.50) больше единицы и их отбрасывание усилит неравенство, тогда условие движения воздуха от узла 2 к узлу 3 будет иметь вид
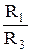 <
< 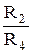 (5.51)
(5.51)
Аналогично можно получить, что для случая движения воздуха от узла 3 к узлу 2 должно соблюдаться неравенство
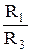 >
> 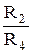 (5.52)
(5.52)
Таким образом, пользуясь формулами (5.44), (5.51), (5.52) можно определить направление движения воздуха в диагонали.
Дата добавления: 2016-01-26; просмотров: 1517;
