Способ последовательных приближений
Уравнения (5.57), (5.58) являются уравнениями двух гипербол. Уравнение (5.57) описывает гиперболу с действительной полуосью «b» параллельной оси «x» и центром, смещенным на –1 по оси «y» (рис.5.16).
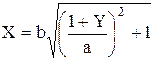 (5.57)
(5.57)
Уравнение (5.58) описывает гиперболу с действительной полуосью «С»параллельной оси «Y» и центром, смещенным на –1 по оси «X»
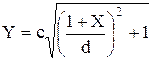 (5.58)
(5.58)
 |
Координаты точки пересечения этих гипербол являются корнями системы (5.57) (5.58). Решая эту систему методом последовательных приближений, задаемся первоначальным значением Х=Х0 и подставляя его в уравнение (5.58), находим приближенное значение Y=Y1. Подставляя значение Y1 в уравнение (5.57), находим более точное значение Х=Х1, которое в свою очередь подставляем в уравнение (5.58), определяя более точное значение Y=Y2. Эта операция повторяется до совпадения двух последующих значений с требуемой степенью точности.
На рис.4.15 стрелками показана схема сходимости к точному корню системы. Из уравнений (5.57) (5.58) и рис. 5.16 видно, что имеет смысл принимать первоначальное значение Х0>b, а Y0>c, что избавит от лишних вычислений.
Графический метод
Систему уравнений (5.57) (5.58) можно решить графически. Для этого, задаваясь произвольным значением «Y» (например 1,2,3 и т. д.) и подставляя его в равенство (5.57) находим значение «Х». По полученным данным строим гиперболу, описываемую уравнением (5.57).
Аналогично задаваясь произвольным значением «х» и подставляя его в уравнение (5.58) получаем значение «y» и строим гиперболу, описываемую уравнением (5.58). Координаты точки пересечения этих графиков и дадут решение системы.
Пример расчета
Заданы сопротивления ветвей простого диагонального соединения и общая депрессия соединения. Определить, расходы воздуха во всех ветвях соединения и сделать проверку полученного результата, используя второй закон расчета вентиляционных сетей
ДАНО:
R1=0.8 km; R2=0.12 km; R3=0.2 km; R4=0.36 km; R5=0.45 km H=300 кг/м2
Определить; Q,q1, q2, q3, q4, q5
Решение задачи
Определим направление движения воздуха в диагонали 2-3.
В нашем примере R1/R3=0.8/0.2=4.0, а R2/R4=0.12/0.36=0.33, следовательно
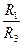 >
> 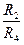 и воздух в диагонали будет двигаться от узла 3 к узлу 2. В этом случае, необходимо изменить обозначения сопротивлений ветвей диагональногосоединения, так как показано на (рис.5.15).
и воздух в диагонали будет двигаться от узла 3 к узлу 2. В этом случае, необходимо изменить обозначения сопротивлений ветвей диагональногосоединения, так как показано на (рис.5.15).
Вычислим по равенствам (5.56) значения вспомогательных величин a,b,c,d.
a= 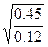 =1.936 b=
=1.936 b= 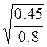 =0.75 c=
=0.75 c= 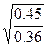 =1.12 d=
=1.12 d= 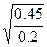 =1.5
=1.5
С учетом полученных значений вспомогательных величин равенства (4.57) (4.58) можно записать в виде
x=0.75 
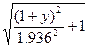 (5.74)
(5.74)
y=  1.12
1.12 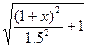 (5.75)
(5.75)
Систему уравнений (5.74) (5.75) решаем методом последовательных приближений. Задаемся первоначальным значением x=x0=1.5 и из уравнения (5.75) определяем значение y1=2.17. По уравнению (5.74) определяем значение x1=1.44 и т. д. y2=2.14, x2=1.43, y3=2.13. Дальнейшие вычисления не имеют смысла. Окончательно принимаем x=1.43, y=2.13
Так как, по условию задачи задана общая депрессия соединения, то для определения общего расхода воздуха и потоков воздуха в ветвях необходимо определить, общее сопротивление диагонального соединения по формуле (5.72)
R0= 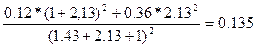 km
km
Определим общий расход воздуха в сети по формуле (5.73)
Q0= 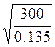 =47.1 м3/с
=47.1 м3/с
Определяем поток воздуха в диагонали по формуле (5.60), а потоки воздуха в остальных ветвях по формулам (5.61-5.64)
q5= 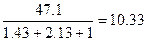 м3/с
м3/с
q2=q5*x=10.33*1.43=14.77 м3/с
q3=q5*y=10.33*2.13=22.0 м3/с
q1=q3+q5=22.0+10.33=32.33 м3/с
q4=q2+q5=14.77+10.33= 25.1 м3/с
Проверяем правильность полученного распределения воздуха, используя второй закон расчета вентиляционных сетей.
Для контура 1-2-3-1 должно выполнятся равенство (5.53), а для контура 2-4-3-2 равенство (5.54)
0.8*14.772- 0.45*10.332-0.12*32.332=0,07=0
0.2*25.12 - 0.36*22.02 +0.45*10.332=-0,2=0
Незначительная невязка по депрессии связана с округлениями при вычислениях.
Дата добавления: 2016-01-26; просмотров: 1083;
