Скорость передачи информации и пропускная способность
Непрерывным каналом называется канал, предназначенный для передачи непрерывных сообщений. Канал считается заданным, если известны статистические данные о сообщениях на его входе и выходе и ограничения, накладываемые на входные сообщения физическими характеристиками канала.
При рассмотрении информационных характеристик канала: (скорости передачи, пропускной способности, коэффициента использования) применяют модель реального канала, называемую гауссовым каналом, предполагая, что по каналу передаются сигналы с постоянной средней мощностью, статистические связи между сигналами и помехой отсутствуют (аддитивная помеха), ширина спектра сигнала и помехи ограничены полосой пропускания канала, а в канале действует флуктуационная помеха ограниченной мощности с равномерным частотным спектром и нормальным распределением амплитуд («белый шум»).
Если X(t) рассматривать как переданный сигнал, Y(t) – как принятый, а
E(t) – как аддитивную помеху в непрерывном канале, то скорость передачи информации по непрерывному каналу (среднее количество информации, которое можно передать по каналу в единицу времени) равна
 , (5.1)
, (5.1)
где
 ; (5.2)
; (5.2)
 ; (5.3)
; (5.3)
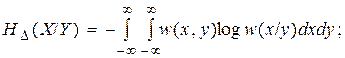 (5.4)
(5.4)
 . (5.5)
. (5.5)
Скорость передачи в предположении, что передаваемые сообщения имеют структуру «белого шума», составит
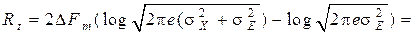
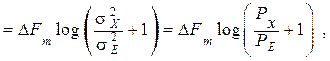 (5.6)
(5.6)
где Рх /РЕ – отношение средних мощностей сигнала и помехи на выходе приёмника; 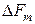 – полоса частот передаваемого сообщения.
– полоса частот передаваемого сообщения.
Пропускная способность (максимальное значение скорости передачи информации по каналу) непрерывного сигнала:
 . (5.7)
. (5.7)
Для гауссова непрерывного канала с дискретным временем
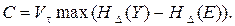 (5.8)
(5.8)
Учитывая, что
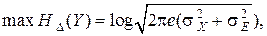 (5.9)
(5.9)
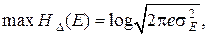 (5.10)
(5.10)
тогда
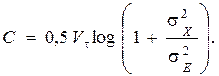 (5.11)
(5.11)
Если в канале нет искажений и помех, то  можно рассматривать как мощность шумов квантования при дискретной передаче непрерывных сигналов. В канале с помехами мощность шумов квантования складывается с мощностью помех, следовательно, в этом случае
можно рассматривать как мощность шумов квантования при дискретной передаче непрерывных сигналов. В канале с помехами мощность шумов квантования складывается с мощностью помех, следовательно, в этом случае  необходимо рассматривать как суммарную мощность помехи и шума квантования. Мощность шума квантования при равномерном квантовании:
необходимо рассматривать как суммарную мощность помехи и шума квантования. Мощность шума квантования при равномерном квантовании:
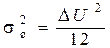 , (5.12)
, (5.12)
где 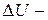 шаг квантования.
шаг квантования.
Для непрерывного канала с непрерывным временем 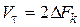 и формула (5.11) переходит в известную формулу Шеннона для пропускной способности гауссова непрерывного канала с флуктуационной помехой:
и формула (5.11) переходит в известную формулу Шеннона для пропускной способности гауссова непрерывного канала с флуктуационной помехой:
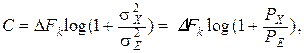 (5.13)
(5.13)
где 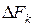 – полоса пропускания канала;
– полоса пропускания канала; 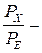 отношение средних мощностей сигнала и помехи на входе приёмника.
отношение средних мощностей сигнала и помехи на входе приёмника.
Из (5.13) следует, что одну и ту же пропускную способность можно получить при различных соотношениях  и
и 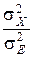 . Кроме того, выражение (5.13) указывает теоретический предел скорости передачи информации по каналу связи при ограниченной средней мощности передаваемых сигналов и при наличии аддитивной помехи в виде "белого шума" с ограниченным спектром.
. Кроме того, выражение (5.13) указывает теоретический предел скорости передачи информации по каналу связи при ограниченной средней мощности передаваемых сигналов и при наличии аддитивной помехи в виде "белого шума" с ограниченным спектром.
Так как энергетический спектр помехи типа "белого шума" равномерен в пределах от 0 до  , мощность РЕ можно выразить через удельную мощность РОШ на единицу частоты. Тогда выражение (5.13) примет вид
, мощность РЕ можно выразить через удельную мощность РОШ на единицу частоты. Тогда выражение (5.13) примет вид
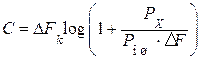 . (5.14)
. (5.14)
При расширении полосы пропускания канала 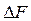 пропускная способность увеличивается, но стремиться к конечному пределу:
пропускная способность увеличивается, но стремиться к конечному пределу:
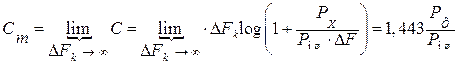 . (5.15)
. (5.15)
Это ограничение, вносимое помехой с уровнем мощности РОШ, которое не может быть превышено без увеличения мощности сигнала.
Если плотность распределения w(x) непрерывных сообщений, вырабатываемых источником информации, отличается от гауссовской, то скорость передачи информации будет меньше.
Необходимо отметить существенную разницу Rt и С. Пропускная способность С характеризует канал, его предельные возможности независимо от системы источник-потребитель, а скорость передачи Rt характеризует некоторую конкретную систему передачи информации.
Кроме того, как следует из (5.13), если сигнал смешан с шумом, то амплитуда сигнала может быть измерена лишь с точностью до эффективного значения шума. Другими словами, неопределенность оценки точного значения амплитуды сигнала равна квадратному корню из среднего квадрата шумового напряжения. Как следует из указанных выше предположений, изменение входного сигнала меньше, чем 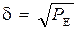 , приемник не различает. Следовательно, число уровней, которое может быть различимо без ошибок, определится из выражения
, приемник не различает. Следовательно, число уровней, которое может быть различимо без ошибок, определится из выражения
 . (5.16)
. (5.16)
Итак, наибольшее количество информации, переносимое каждым импульсом, имеющим М различных уровней, равно
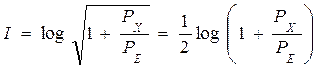 . (5.17)
. (5.17)
Дата добавления: 2016-02-04; просмотров: 1588;
