Энтропия источника и энтропия сообщения

Пусть источник информации выдаёт дискретные сообщения Z. С помощью кодирующего устройства каждое сообщение превращается в код. Множество символов кода обозначим через X. Если исследуется канал связи, то можно не обращаться к источнику информации, а рассматривать лишь источник символов (кодирующее устройство). Тогда возникает необходимость связать свойства источника и отправителя. Эта связь возможна через энтропию.

Под энтропией сообщения будем понимать количество информации, содержащееся в любом усреднённом сообщении. Тогда

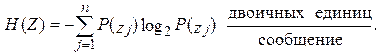(6.4)

– усреднённая энтропия сообщения. Соответственно энтропия источника, или количество информации, содержащееся в одном символе сообщения:

(6.5)

Пример. Пусть передаётся четыре равновероятных сообщения двоичным не избыточным кодом. Сообщения отображаются кодом 00, 01,10,11. Найдём энтропию сообщения:

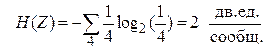
и энтропию источника

.

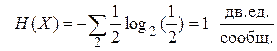Из примера видно, что каждый символ несёт одну двоичную единицу информации.

Разделим H(Z) на H(X) и получим число элементов в коде, т.е. H(Z)/H(X) = n. Если данное условие соблюдается, то код называется оптимальным, в противном случае в коде возникает избыточность, и он становится неоптимальным для канала без шума. Для получения оптимального кода необходимо, чтобы символы в нём встречались с равной вероятностью.