Дискретный канал без помех

В любом реальном канале всегда присутствуют помехи. Однако если их уровень настолько мал, что вероятность искажения практически равна нулю, можно считать, что все сигналы передаются не искажёнными. В этом случае среднее количество информации, переносимое одним символом, определяется по формуле

I(Y,X) = I(X,Y) = H(X), (6.6)

а максимальное значение

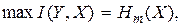(6.7)

где H_m(X) – максимальная энтропия источника сигналов, получающаяся при равномерном распределении вероятностей символов алфавита источника

P(X₁) = P(X₂) = … = P(X_m) = 1/m. (6.8)

Но максимальная энтропия выражается в единицах информации на символ сигнала, как

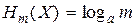. (6.9)

Следовательно, пропускная способность дискретного канала без помех в единицах информации за единицу времени равна

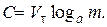(6.10)

Шенноном сформулирована основная теорема о кодировании, которая утверждает, что если источник информации имеет энтропию H(Z) единиц информации на символ сообщения, а канал связи обладает пропускной способностью С единиц информации в единицу времени, то:

1) сообщения, вырабатываемые источником, всегда можно закодировать так, чтобы скорость Vz их передачи была сколь угодно близкой к

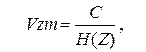(6.11)

где измеряется в символах сообщения за единицу времени;

2) не существует метода кодирования, позволяющего сделать эту скорость больше чем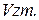

Согласно сформулированной теореме существует метод кодирования, позволяющий пр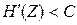и и 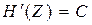передавать всю информацию, вырабатываемую источником, а при такого метода не существует, где 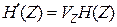– поток информации.