Дискретный канал с помехами

Дискретный канал с помехами характеризуется условными вероятностями P(y_j/x_i) того, что будет принят сигнал y_j, если передан x_i, т.е. матрицей

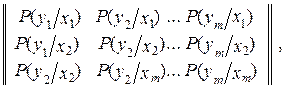(6.12)

при отсутствии помех все P(y_j/x_i) при j # i равны 0 и при j = i равны 1.

Среднее количество информации на символ, получаемое при приёме одного элементарного сигнала равно:

I(Y,X) = H(Y) – H(Y/X). (6.13)

В случае независимости отдельных символов сигнала энтропия на выходе линии

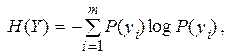(6.14)

предполагается, что число букв алфавита Y = (y₁, y₂, …, y_m) равно числу букв алфавита X = (x₁, x₂, …, x_m) и равно, следовательно, m.

Средняя условная энтропия:

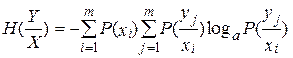. (6.15)

Пропускная способность канала высчитывается по формуле

C = V_t max I(Y,X) , (6.16)

где максимум определяется по всем возможным распределениям вероятностей, характеризующим источник сигналов

Пусть требуется определить пропускную способность канала связи, по которому передаются двоичные сигналы со скоростью V_t, если вероятность превращения в результате действия помех каждого из этих сигналов в противоположный равна Р (вероятность правильного приёма, следовательно, I-P), передаваемые символы предполагаются независимыми.

В этом случае алфавит X и алфавит Y состоит из двух символов:

X = (x₁, x₂), Y = (y₁, y₂).

Диаграмма (рис. 6.4) показывает возможные варианты передачи и соответствующие им вероятности.

Канал такого типа носит название симметричного.

Средняя условная энтропия:

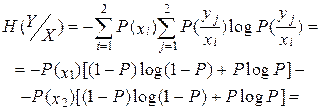
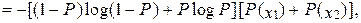(6.17)

но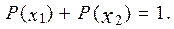

Поэтому

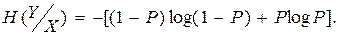(6.18)

Отсюда видно, что 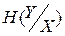не зависит от характеристик источника, т.е. от P(x₁) и P(x₂), и определяется только помехами в канале передачи.

Максимальное количество информации на один символ получается при таком распределении вероятностей P(x_i), при котором оказывается максимальным член H(Y). Но H(Y) не может превосходить величины

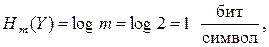
что достигается при P(x₁) = P(x₂) 1/2. Поэтому имеем

max (I(Y,X)) = 1 + PlogP + (1-P) log(1-P)

и, следовательно, пропускная способность:

C = V_t max(I(Y,X)) = V_t [1+ PlogP + (1-P) log(1-P)]. (6.19)

Отсюда следует: в частности, что при Р = 0, т.е. при отсутствии шумов в канале связи, имеем

Cmax =V_t.

При P = 1 также имеем детерминированный случай, когда сигналы x₁ превращаются в сигналы x₂ и наоборот с вероятностью, равной единице. При этом пропускная способность канала также максимальная:

Cmax = V_t.

Минимальное значение пропускная способность имеет при P1/2.

В этом случае независимо от полученных сигналов ничего нельзя сказать о том, какой сигнал был послан: имеет место такая ситуация, как если бы в линию связи вообще не посылались сигналы. Тогда, естественно, пропускная способность

Cmin = 0.