Эффективное кодирование при неизвестной статистике сообщений

Коды, эффективные одновременно для некоторого класса источников, называют универсальными кодами. Сформулируем постановку задачи универсального кодирования источников. Предположим, что алфавит состоит из двух X₁ и X₂, появляющихся независимо, с вероятностями p и g = 1-p. Однако величина р заранее неизвестна. Требуется построить код, для которого среднее число символов «0» и «1» на одну букву алфавита приближалось бы к H(X) при любом р, . Этот код строится так. Множество всех блоков длины n в алфавите X разбиваем на группы, которые имеют одинаковые вероятности при любом p. Таких групп будет n+1. В нулевой группе отсутствует буква X₂, она состоит из единственного блока X₁X₁X₁…X₁, вероятность появления которого pⁿ. Первая группа состоит из блоков длиной n, содержащих одну букву X₂. 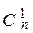Эта группа состоит из = n блоков, вероятность каждого из которых равна 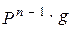. Группы с номером k состоят из всех блоков длиной n, содержащих k букв X₂. Эта группа содержит n блоков, вероятность каждого из которых .

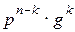Универсальный код для k-й группы состоит из двух частей: префикса и суффикса. Префикс содержит log(n+1) двоичных знаков. Префикс указывает, к какой группе сообщений принадлежит кодируемый блок, суффикс содержит 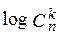двоичных символов и указывает номер блока в группе.

Построенный таким образом код будет однозначно дешифрируем. На приемном конце первоначально по log(n+1) элементам кода определяют, к какой группе принадлежит переданное сообщение, а затем по следующим 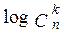элементам определяют, какое именно сообщение передавалось.

Код в табл. 7.8 построен описанным выше способом. Здесь выделены штриховой линией префиксы.

Из приведенного выше описания метода кодирования видно, что наиболее трудоемкой частью кодирования является нахождение суффикса. Опишем алгоритм нахождения суффикса. Пусть в блоке X длиной n буква X₁ встречается на местах i₁,i₂,…,i_r, тогда суффиксом для X назовем число N(x), вычисляемое по правилу

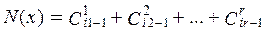, (7.13)

очевидно, что блоки с разными наборами (i₁, i₂,…, i_r) получают разные номера. При этом максимально значение номера 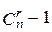. Таким образом, двоичная запись номера (суффикса) должна иметь длину .

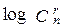Для нахождения N(x) воспользуемся таблицей биноминальных коэффициентов (треугольником Паскаля):

8 7 21 35 35 21 7 1 0

7 6 15 20 15 6 1 0

6 5 10 10 5 1 0

5 4 6 4 1 0

4 3 3 1 0

3 2 1 0

2 1 0

1 0

Таблица 7.8

Построение префиксного кода

Кодируемые слова	Номер группы	Вероятность слова	Код
X₁X₁X₁X₁	1	Р⁴
X₁X₁X₁X₂			001 00
X₁X₁X₂X₁		Р³g	001 01
X₁X₂X₁X₁			001 10
X₂X₁X₁X₁			001 11
Кодируемые слова	Номер группы	Вероятность слова	Код
X₁X₂X₁X₂			010 001
X₂X₁X₁X₂		Р²g²	010 010
X₁X₂X₂X₁			010 011
X₂X₁X₂X₁			010 100
X₂X₂X₁X₁			010 101
X₂X₂X₂X₁			011 00
X₂X₂X₁X₂		Рg²	011 01
X₂X₁X₂X₂			011 10
X₁X₂X₂X₂			011 11
X₂X₂X₂X₂		g⁴

Элементы этой таблицы вычисляются по мере надобности либо размещаются в памяти кодирующего устройства.

Приведем фрагмент этой таблицы, в которой на пересечении i-й строки и
j-го столбца стоит .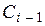

Пример 7.1. Пусть n = 8, X = X₂X₁X₁X₂X₁X₁X₂X₁, тогда r = 5; i₁=2; i₂ = 3; i₃ = 5; i₄ = 6; i₅ = 8. Номер блока 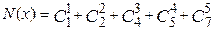. Слагаемые в N(x) находим, используя таблицу дополнительных коэффициентов. Таким образом, N(x) = 1 + 1 + 4 + 5 + 21 = 32 или в двоичной записи N(x) = 100000. Декодирование производится с помощью этой же таблицы.

Пример 7.2. Пусть нам известно, что длина передаваемого блока равна 8, и что в блоке пять букв X_i (количество букв в блоке находим по префиксу). Находим максимальное число в пятом столбце, не превосходящее 32, это следовательно, i₅ = 8, находим разность 32 – 21 = 11. Находим далее максимальное число четвертого столбца, не превосходящее 11. Это 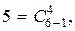т.е. i₄ = 6. Аналогично находим i₃= 5, i₂=3, i₁=2. Следовательно, декодированное сообщение имеет вид X = X₂X₁X₁X₂X₁X₁X₂X₁, т.е. совпадает с переданным.

Рассмотренные кодирование и декодирование достаточно просто осуществляются с помощью специализированных вычислительных устройств.

Контрольные вопросы

1. Какие кодовые слова называются неперекрываемыми?

2. Запишите выражение для средней длины кодового слова?

3. Сформулируйте теорему существования.

4. Поясните принцип кодирования сообщений в коде Шеннона-Фано.

5. Поясните принцип кодирования сообщений в коде Хаффмана.

6. Сравните код Шеннона-Фано и код Хаффмана.

7. В чем преимущество кодирования групп сообщений?

8. Какие коды называются префиксными?

9. Перечислите недостатки систем эффективного кодирования.

10. Поясните принцип эффективного кодирования при неизвестной статистике сообщений.

СЖАТИЕ СООБЩЕНИЙ

Типы систем сжатия

Передача и хранение информации требуют достаточно больших затрат. И чем с большим количеством информации нам приходится иметь дело, тем дороже это стоит. К сожалению, большая часть данных, которые нужно передавать по каналам связи и сохранять, имеет не самое компактное представление. Скорее, эти данные хранятся в форме, обеспечивающей их наиболее простое использование, например: обычные книжные тексты, ASCII коды текстовых редакторов, двоичные коды данных ЭВМ, отдельные отсчеты сигналов в системах сбора данных и т.д. Однако такое наиболее простое в использовании представление данных требует вдвое - втрое, а иногда и в сотни раз больше места для их сохранения и полосу частот для их передачи, чем на самом деле нужно. Поэтому сжатие данных – это одно из наиболее актуальных направлений современной телемеханики. Таким образом, цель сжатия данных - обеспечить компактное представление данных, вырабатываемых источником, для их более экономного сохранения и передачи по каналам связи.

Ниже приведена условная структура системы сжатия данных:

Данные источника®Кодер®Сжатые данные®Декодер®Восстановленные данные

В этой схеме вырабатываемые источником данные определим как данные источника, а их компактное представление - как сжатые данные. Система сжатия данных состоит из кодера и декодера источника. Кодер преобразует данные источника в сжатые данные, а декодер предназначен для восстановления данных источника из сжатых данных. Восстановленные данные, вырабатываемые декодером, могут либо абсолютно точно совпадать с исходными данными источника, либо незначительно отличаться от них.

Существуют два типа систем сжатия данных:

- системы сжатия без потерь информации (неразрушающее сжатие);

- системы сжатия с потерями информации (разрушающее сжатие)

В системах сжатия без потерь декодер восстанавливает данные источника абсолютно точно, таким образом, структура системы сжатия выглядит следующим образом:

Вектор данных X ® Кодер ® B (X) ® Декодер ® X

Вектор данных источника X, подлежащих сжатию, представляет собой последовательность X = (x₁, x₂,… x_n ) конечной длины. Отсчеты x_i - составляющие вектора X - выбраны из конечного алфавита данных A. При этом размер вектора данных n ограничен, но он может быть сколь угодно большим. Таким образом, источник на своем выходе формирует в качестве данных X последовательность длиной n из алфавита A .

Выход кодера - сжатые данные, соответствующие входному вектору X, - представим в виде двоичной последовательности B(X) = ( b₁,b₂,…b_k ), размер которой k зависит от X. Назовем B(X) кодовым словом, присвоенным вектору X кодером (или кодовым словом, в которое вектор X преобразован кодером). Поскольку система сжатия - неразрушающая, одинаковым векторам X_l = X_m должны соответствовать одинаковые кодовые слова B(X_l ) = = B(X_m ).

При решении задачи сжатия естественным является вопрос, насколько эффективна та или иная система сжатия. Поскольку, как мы уже отмечали, в основном используется только двоичное кодирование, то такой мерой может служить коэффициент сжатия r, определяемый как отношение

размер данных источника в битах

r= (8.1)

размер сжатых данных в битах

Таким образом, коэффициент сжатия r = 2 означает, что объем сжатых данных составляет половину от объема данных источника. Чем больше коэффициент сжатия r, тем лучше работает система сжатия данных.

Наряду с коэффициентом сжатия rэффективность системы сжатия может быть охарактеризована скоростью сжатия R,определяемой как отношение

R = k/n(8.2)

и измеряемой в «количестве кодовых бит, приходящихся на отсчет данных источника». Система, имеющая больший коэффициент сжатия, обеспечивает меньшую скорость сжатия.

В системе сжатия с потерями (разрушением) кодирование производится таким образом, что декодер не в состоянии восстановить данные источника в первоначальном виде. Структурная схема системы сжатия с разрушением выглядит следующим образом:

X ® Квантователь ® X^q® Неразрушающий кодер ® B (X^q)® Декодер ® X*

Как и в предыдущей схеме, X = ( x₁, x₂,… x_n ) - вектор данных, подлежащих сжатию. Восстановленный вектор обозначим как X* = ( x₁, x₂,… x_n ). Отметим наличие в этой схеме сжатия элемента, который отсутствовал при неразрушающем сжатии, - квантователя.

Квантователь применительно к вектору входных данныхXформирует вектор X^q, достаточно близкий к X в смысле среднеквадратического расстояния. Работа квантователя основана на понижении размера алфавита (простейший квантователь производит округление данных до ближайшего целого числа).

Далее кодер подвергает неразрушающему сжатию вектор квантованных данных X^q таким образом, что обеспечивается однозначное соответствие между X^q и B(X^q)(для X_l^q = X_m ^qвыполняется условиеB (X_l^q) = B (X_m^q)). Однако система в целомостается разрушающей, поскольку двум различным векторам Xможет соответствовать один и тот же вектор X*.

Разрушающий кодер характеризуется двумя параметрами - скоростью сжатия R и величинойискажений D, определяемых как

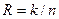.(8.3)

Параметр R характеризует скорость сжатия в битах на один отсчет источника, величина D является мерой среднеквадратического различия между X* иX.

Если имеются система разрушающего сжатия со скоростью и искажениями R₁и D₁ соответственно и вторая система со скоростью R₂ и искажениями D_2,то первая из них лучше, если R₁‹ R₂и D₁‹ D₂. Однако, к сожалению, невозможно построить систему разрушающего сжатия, обеспечивающую одновременно снижение скорости R и уменьшение искажений D, поскольку эти два параметра связаны обратной зависимостью. Поэтому целью оптимизации системы сжатия с потерями может быть либо минимизация скорости при заданной величине искажений, либо получение наименьших искажений при заданной скорости сжатия.

Выбор системы неразрушающего или разрушающего сжатия зависит от типа данных, подлежащих сжатию. При сжатии текстовых данных, компьютерных программ, документов, чертежей и т.п. совершенно очевидно, что нужно применять неразрушающие методы, поскольку необходимо абсолютно точное восстановление исходной информации после ее сжатия. При сжатии речи, музыкальных данных и изображений, наоборот, чаще используется разрушающее сжатие, поскольку при практически незаметных искажениях оно обеспечивает на порядок, а иногда и на два меньшую скорость R. В общем случае разрушающее сжатие обеспечивает, как правило, существенно более высокие коэффициенты сжатия, нежели неразрушающее.

Ниже приведены ряд примеров, иллюстрирующих необходимость процедуры сжатия.

Пример 8.1. Предположим, что источник генерирует цифровое изображение (кадр) размером 512*512 элементов, содержащее 256 цветов. Каждый цвет представляет собой число из множества {0,1,2… 255}. Математически это изображение представляет собой матрицу 512х512, каждый элемент которой принадлежит множеству {0,1,2… 255}. (Элементы изображения называют пикселами).

В свою очередь, каждый пиксел из множества {0,1,2… 255} может быть представлен в двоичной форме с использованием 8 бит. Таким образом, размер данных источника в битах составит 8х512х512= 2²¹, или 2,1 Мегабита.

На жесткий диск объемом в 1 Гигабайт поместится примерно 5000 кадров изображения, если они не подвергаются сжатию (видеоролик длительностью примерно в пять минут). Если же это изображение подвергнуть сжатию с коэффициентом r = 10, то на этом же диске мы сможем сохранить уже почти часовой видеофильм!

Предположим далее, что мы хотим передать исходное изображение по телефонной линии, пропускная способность которой составляет 14000 бит/с. На это придется затратить 21000000 бит/14000 бит/с, или примерно 3 минуты. При сжатии же данных с коэффициентом r = 40 на это уйдет всего 5 секунд!

Пример 8.2.В качестве данных источника, подлежащих сжатию, выберем фрагмент изображения размером 4х4 элемента и содержащее 4 цвета: R = ="красный", O = "оранжевый", Y = "синий", G = "зеленый":

R R O Y

R O O Y

O O Y G

Y Y Y G

Просканируем это изображение по строкам и каждому из цветов присвоим соответствующую интенсивность, например, R = 3, O = 2, Y = 1 и G = 0, в результате чего получим вектор данных X = (3,3,2,1,3,2,2,1,2,2,1,0,1,1,1,0).

Для сжатия данных возьмем кодер, использующий следующую таблицу перекодирования данных источника в кодовые слова (вопрос о выборе таблицы оставим на будущее):

Кодер

Отсчет Кодовое слово

Используя таблицу кодирования, заменим каждый элемент вектора X соответствующей кодовой последовательностью из таблицы (так называемое кодирование без памяти). Сжатые данные (кодовое слово B(X))будут выглядеть следующим образом:

B(X) =( 0,0,1,0,0,1,0,1,1,0,0,1,0,1,0,1,1,0,1,0,1,1,0,0,0,1,1,1,0,0,0).

Коэффициент сжатия при этом составит r = 32/31, или 1,03. Соответственно скорость сжатия R = 31/16 бит на отсчет.

<27 28 293031 32 33 >

Дата добавления: 2016-02-04; просмотров: 1185;