Квантование по времени и по уровню.
При преобразовании аналоговой величины в код квантование осуществляется с заданными шагами как по времени, так и по уровню.
На рис. 1.15 показано, как производится квантование по уровню и по времени функции f(t). Сначала проводят линии, параллельные вертикальной оси f(t) с шагом Dt, затем параллельные горизонтальной оси t с шагом q.
Квантование осуществляют заменой через шаг Dt значений функции f(t) ближайшим дискретным уровнем. Этот уровень и является тем дискретным значением, которое заменяет значение функции в данный дискретный момент времени.
Если необходимо представить себе ступенчатую ломаную линию, которая в результате квантования заменяет непрерывную функцию, все полученные точки следует соединить так, как сделано на рис. 1.15.
 |
| Цифровой эквивалент | |||||||||||||||||||||||
Рис. 1.15. Преобразование непрерывной величины в код
Различают равномерное и неравномерное квантование. В большинстве случаев применяется и далее подробно рассматривается равномерное квантование (рис. 1.16), при котором шаг квантования постоянный: q = fi - fi-1 = const; однако иногда определенное преимущество дает неравномерное квантование, при котором шаг квантования qiразный для различных fi (рис. 1.17).
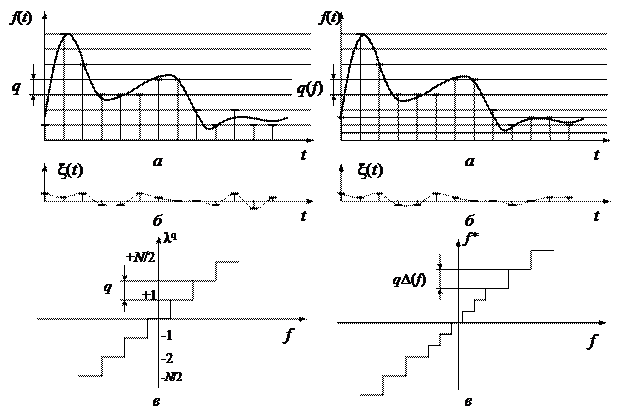 |
| Рис. 1.16. Квантование по уровню равномерное: а - процесс квантования; б - погрешность квантования; в - характеристика квантования. | Рис. 1.17. Квантование по уровню неравномерное: а - процесс квантования; б - погрешность квантования; в - характеристика квантования. |
Квантование приводит к искажению сообщений. Так как наименее точно функция передается в точке, находящейся между двумя уровнями квантования и отстоящей от них на половину интервала квантования q/2, то максимальная ошибка квантования по уровню
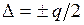 , (1.37)
, (1.37)
а мощность шума квантования при равномерном квантовании
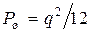 (1.38)
(1.38)
При достаточно большом числе уровней квантования N распределение погрешности квантования в пределах от – q/2 до + q/2 будет равномерным независимо от закона распределения самой функции f(t). Среднеквадратичное значение погрешности квантования по уровню
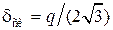 , (1.39)
, (1.39)
т.е. в 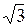 раз меньше максимальной.
раз меньше максимальной.
Что касается точности преобразования (квантования), то обычно она задается в виде приведенной относительной погрешности 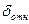 в процентах. По определению,
в процентах. По определению, 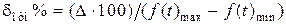 . Подставив значение D из (1.37), получим выражение для шага квантования при
. Подставив значение D из (1.37), получим выражение для шага квантования при 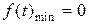
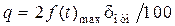 . (1.40)
. (1.40)
После того как непрерывное сообщение с помощью квантования будет преобразовано в дискретное сообщение, необходимо каждому его уровню присвоить цифровой эквивалент, как правило, в двоичном неизбыточном коде (см. рис. 1.15) и передать по каналу связи. При этом, если известен шаг квантования q, то число уровней квантования N и число разрядов кодовой комбинации K при 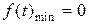 можно определить из выражения
можно определить из выражения
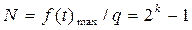 . (1.41)
. (1.41)
Пример 1. Предположим, что необходимо произвести квантование непрерывной функции, изменяющейся от нуля до 100 В, с точностью 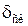 = 1%. Определить величину шага квантования, число уровней квантования и число разрядов кодовой комбинации. Согласно (1.40),
= 1%. Определить величину шага квантования, число уровней квантования и число разрядов кодовой комбинации. Согласно (1.40), 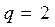 В. Из (1.41) определим, что необходимо 50 уровней квантования, а число разрядов
В. Из (1.41) определим, что необходимо 50 уровней квантования, а число разрядов 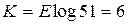 . Такое число уровней устанавливается, если измерение в данной точке производят до ближайшего уровня (нижнего или верхнего). При схемной реализации отсчет часто производят до какого-нибудь одного уровня (только нижнего или только верхнего). В этом случае для обеспечения точности квантования в 1% от 100 В число уровней следует взять 100, так как
. Такое число уровней устанавливается, если измерение в данной точке производят до ближайшего уровня (нижнего или верхнего). При схемной реализации отсчет часто производят до какого-нибудь одного уровня (только нижнего или только верхнего). В этом случае для обеспечения точности квантования в 1% от 100 В число уровней следует взять 100, так как 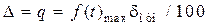 , а следовательно k = 7.
, а следовательно k = 7.
Контрольные вопросы
1. Какой сигнал называется регулярным?
2. Запишите выражение для периодичного сигнала.
3. Какой сигнал называется не периодическим?
4. Приведите временную диаграмму для дискретного сигнала.
5. Запишите ряд Фурье для периодичного сигнала.
6. Что означает представление сигнала с заданным периодом рядом Фурье?
7. Приведите спектр периодически повторяющихся прямоугольных импульсов.
8. Приведите выражение для средней мощности периодических прямоугольных импульсов.
9. Что понимается под практической шириной спектра сигнала?
10. Приведите форму сигнала при ограничении спектра прямоугольных импульсов, имеющих скважность Q =3 и ограниченных третьей гармонической составляющей.
11. Приведите выражение для спектра непериодического сигнала.
12. Поясните график зависимости энергии импульсов от ширины сохраняемой части спектра.
13. Сформулируйте теорему В.А. Котельникова о преобразовании непрерывных сообщений в дискретные сигналы.
14. Сформулируйте теорему дискретизации для двумерных сигналов.
Дата добавления: 2016-02-04; просмотров: 5470;
