Практическая ширина спектра.

Теоретически, как указывалось выше, для большинства периодических функций спектр неограничен, т.е. для передачи сигналов телемеханики без изменения формы необходимы бесконечно большая полоса пропускания канала связи и отсутствие амплитудных и фазовых искажений. Практически все каналы связи имеют ограниченную полосу пропускания, и форма сигналов при передаче по каналу изменяется даже при отсутствии в этой полосе амплитудных и фазовых искажений. Очевидно, важно передать ту часть спектра сигнала, которая содержит гармонические составляющие с относительно большими амплитудами. В связи с этим вводится понятие практической ширины спектра сигнала. Под практической шириной спектра сигнала понимается та область частот, в пределах которой лежат гармонические составляющие сигнала с амплитудами, превышающими наперед заданную величину.

Поскольку средняя мощность, выделяемая сигналом на активном сопротивлении, равном 1 Ом, складывается из мощностей, выделяемых на этом сопротивлении гармоническими составляющими,

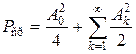, (1.20)

практическая ширина спектра с энергетической точки зрения может быть определена как область частот, в пределах которой сосредоточена подавляющая часть мощности сигнала.

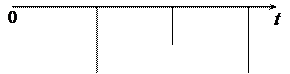
В качестве примера определим практическую ширину спектра периодической последовательности прямоугольных импульсов (рис. 1.8,а), если требуется учесть все гармонические составляющие сигнала, амплитуды которых более 0,2 от амплитуды первой гармоники. Число подлежащих учету гармоник k может быть получено из выражения

,

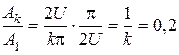откуда k = 5.

Таким образом, практическая ширина спектра в рассмотренном примере оказывается равной 5W₁, в ней размещаются всего три гармоники (первая, третья и пятая) и постоянная составляющая.

Средняя мощность P_k5, выделяемая в активном сопротивлении, равном 1 Ом, перечисленными составляющими, равна

.

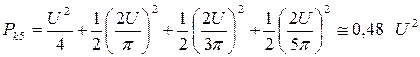Средняя мощность, выделяемая в этом же сопротивлении всеми составляющими сигнала, будет

.

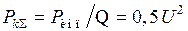Таким образом, 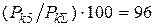%, т.е. составляющие, входящие в практический спектр, выделяют в активном сопротивлении 96 % всей мощности сигнала.

Очевидно, расширение практического спектра данного сигнала (свыше 5W₁) с энергетической точки зрения нецелесообразно.

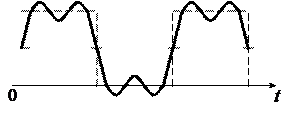
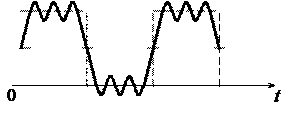
Ограничение спектра сигнала оказывает также влияние на его форму. Для иллюстрации на рис. 1.8 показано изменение формы прямоугольных импульсов при сохранении в спектре только постоянной составляющей и первой гармоники (рис. 1.8, б), при ограничении спектра частотой 3W₁ (рис. 1.8, в) и при ограничении спектра частотой 5W₁ (рис. 1.8, г). Как следует из рисунка, чем круче должен быть фронт импульса, тем большее число высших гармонических составляющих должно входить в состав сигнала.

A₀+A₁(t)

U

T/2

T

		б
		a

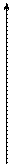
A₀+A₁(t)+A₃(t) A₀+A₁(t)+A₃(t)+A₅(t)

		в		г

Рис. 1.8. Формы сигнала при ограничении спектра последовательности

прямоугольных импульсов

Рассмотренная зависимость формы периодического сигнала от количества суммируемых гармоник показывает, что при выборе практической ширины спектра сигнала нельзя ограничиваться только энергетическими соображениями. Необходимо учитывать требования к сигналу на выходе системы, как с энергетической точки зрения, так и с точки зрения сохранения его формы. В общем случае практическая ширина спектра сигнала выбирается из условия

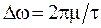, (1.21)

где m = 0,5… 2 – коэффициент формы импульса; при m = 1 обеспечивается передача около 90 % всей энергии сигнала.

В кодоимпульсных системах телеизмерения, а также во многих системах телеуправления каждая кодовая комбинация состоит из определенной последовательности прямоугольных импульсов и пауз. Кодовая комбинация, соответствующая данной величине измеряемого параметра или команде, может периодически передаваться по каналу связи. Спектр такого сигнала зависит, конечно, от того какая именно кодовая комбинация передается. Но самым главным фактором, определяющим удельный вес высших гармоник спектра, остается наибольшая частота следования импульсов. Поэтому и для кодоимпульсных систем при определении практически необходимой ширины полосы частот выбирают сигнал в виде периодической последовательности прямоугольных импульсов (рис. 1.5). Параметр t выбирают равным длительности самого короткого импульса среди всех встречающихся в кодовых комбинациях, период следования T = 2t. В этом случае наибольшая частота следования импульсов W_max = 2p / T и частота основной гармоники спектра W₁ = W_max. Необходимая ширина полосы частот сигнала определяется дискретным спектром с ограниченным числом составляющих и в соответствии с выражением (1.21).

Характер спектра, определяющий требуемую полосу частот, зависит не только от вида сигнала, но и от условий, существующих в тракте передачи. Если переходные процессы, возникающие в системе при передаче одного импульса, заканчиваются до момента возникновения следующего импульса, то вместо периодической последовательности импульсов можно рассматривать передачу независимых одиночных импульсов.