Периодические сигналы

Представление периодического сигнала суммой гармонических составляющих осуществляется с помощью разложения в ряд Фурье функции (1.1), которая является временным представлением сигнала. Если функция f(t)задана на интервале времени t₁£ t£ t₂и повторяется с периодом T=2p/W₁= t₂ - t₁, то тригонометрическая форма ряда Фурье для нее может быть записана следующим образом:

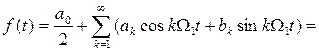
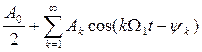= , k = 1, 2, …. (1.5)

Амплитуды косинусоидальных и синусоидальных членов в разложении (1.5) определяются выражениями:

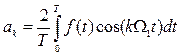; (1.6)

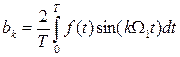. (1.7)

Слагаемое

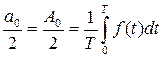(1.8)

является постоянной составляющей сигнала, которая, как это следует из (1.8), равна среднему значению функции f(t) за период.

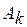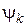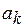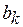Амплитуда и фаза k-й гармоники, как это следует из (1.5), связаны с величинами и соотношениями:

, , ;

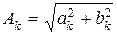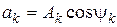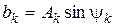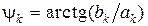. (1.9)

Весьма удобной является комплексная форма записи ряда Фурье, к которой легко перейти, если в разложении (1.5) выразить тригонометрические функции через показательные, воспользовавшись известными формулами:

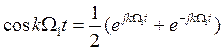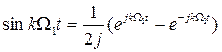; . (1.10)

В результате получим

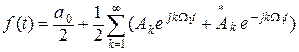, (1.11)

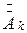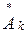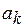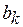где и – комплексные амплитуды, связанные с и соотношениями

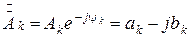, (1.12)

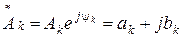. (1.13)

Таким образом, комплексные амплитуды 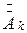и 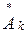являются комплексно-сопряженными величинами. Действительно, каждое слагаемое первого ряда в выражении (1.11) можно представить как вектор на комплексной плоскости (рис. 1.4), вращающийся с частотой kW₁ (т.е. в положительном направлении отсчета углов – против направления движения часовой стрелки). Каждое слагаемое второго ряда – вектор, вращающийся в обратном направлении.

Рис. 1.4. Векторная диаграмма комплексно-сопряженных величин

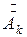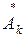Так как и – комплексно-сопряженные величины, то сумма векторов в любой момент времени дает вектор, направленный по вещественной оси, т.е. k-ю гармоническую составляющую вещественной функции времени f(t). Отрицательная частота – kW₁ только указывает направление вращения вектора.

Комплексная амплитуда 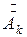определяется по выражению

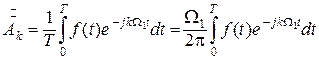. (1.14)

При k = 0

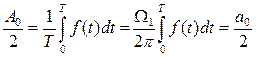. (1.15)

Тогда выражение (1.11) можно переписать в виде

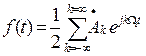. (1.16)

При такой записи ряда Фурье периодический сигнал заменяется суммой простых гармонических колебаний как с положительными частотами (k > 0), так и с отрицательными (k < 0). Конечно, отрицательные частоты не имеют здесь физического смысла, а являются формальным следствием произведенного математического преобразования.

1.3. Спектры периодических сигналов и необходимая
ширина полосы частот

Дискретный спектр.

Представить сигнал с заданным периодом T рядом Фурье – это значит найти амплитуды и начальные фазы всех его гармонических составляющих. Совокупность амплитуд называют спектром амплитуд, а совокупность начальных фаз – спектром фаз. Во многих частных случаях достаточно рассчитать только спектр амплитуд сигнала, который для краткости назовем просто спектром.

Определим спектр периодической последовательности прямоугольных импульсов (рис. 1.5) длительностью t и с периодом T. Напряжение такой формы действует в каналах связи и часто рассматривается как основной периодический сигнал при исследовании передачи информации по линии связи.

u(t)

U

t

t₁ 0 t₂

T τ

Рис. 1.5. Периодическая последовательность прямоугольных импульсов

Для такого сигнала по формулам (1.6) – (1.8)

; ;

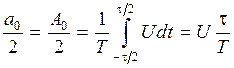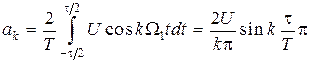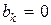, т.е. 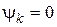или p и .

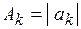Следовательно, напряжение можно представить рядом Фурье

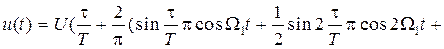
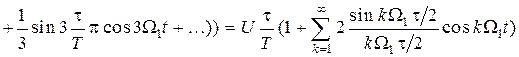. (1.17)

Спектр амплитуд сигнала изображают в виде спектральных линий, длины которых пропорциональны амплитудам гармоник (рис. 1.6).

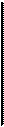
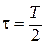
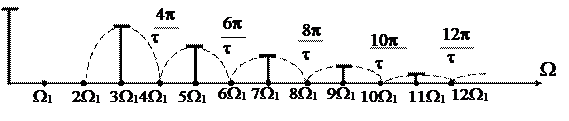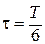
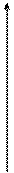
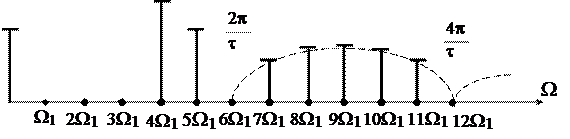
Рис. 1.6. Спектры периодически повторяющихся прямоугольных импульсов

при Q=2 и Q=6

Такой спектр называют линейчатым или дискретным. Спектр фаз 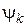также линейчатый, причем в рассматриваемом частном случае 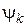может иметь только два значения: 0 или p.

Непрерывная кривая, соединяющая концы линий спектра и показанная на рис. 1.5 пунктиром, носит название огибающей спектра амплитуд, которая определяется уравнением

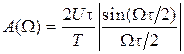, (1.18)

где W = kW₁ для k-й гармоники.

Выражение для фазы гармоники можно записать в виде

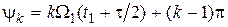. (1.19)

На рис. 1.7 приведены спектры фаз и их огибающие при различно выбранных началах отсчета времени. Наиболее простым получается спектр фаз при .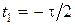

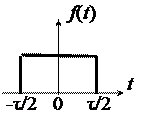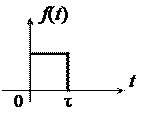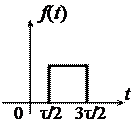Рис. 1.7. Спектры фаз при различных началах отсчета времени

Кроме того, из (1.17) и рис. 1.6 следует, что периодическую последовательность прямоугольных импульсов можно рассматривать как результат наложения друг на друга бесконечного количества гармоник с частотами, кратными основной частоте W₁= 2p/T, а также постоянной составляющей. Амплитуды гармонических составляющих кратных скважности Q равны нулю (например, равны нулю амплитуды четных гармоник на рис. 1.6, где принято t = T/2, и шестая, двенадцатая и т.д., где принято t = T/6).

С изменениями длительности импульса t при том же периоде следования импульсов T или с изменением периода T при постоянной длительности t спектр существенно преобразуется. Если длительность импульса растет, то увеличивается удельный вес постоянной составляющей и гармоник с небольшими порядковыми номерами, а удельный вес высших гармоник падает. Если, наоборот, уменьшить длительность импульса t, то удельный вес гармоник с небольшим порядковым номером уменьшается, а удельный вес высших гармоник растет.

При изменении не длительности импульсов t, а периода их повторения T спектр амплитуд становится реже или гуще. Так, с увеличением периода T основная частота уменьшается (W₁= 2p /T) и спектр становится гуще.