Глава VI. ПЕРИОДИЧЕСКИЕ РЕЖИМЫ ТЕПЛОВОГО ВОЗДЕЙСТВИЯ НА ОДНОМЕРНЫЙ ПОЛУБЕСКОНЕЧНЫЙ МАССИВ ПРИ ГРАНИЧНЫХ УСЛОВИЯХ III РОДА.

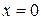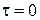Пусть на границе полубесконечного одномерного массива с начальным однородным распределением температур имеет место теплообмен при граничных условиях IIIрода с жидкостью, температура которой в момент времени начинает изменяться по синусоидальному закону.

В математической постановке задача выглядит следующим образом:

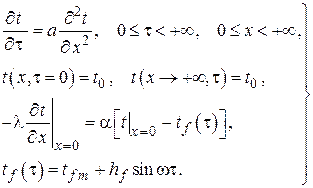
Здесь 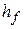– амплитудное значение отклонения температуры жидкости от начальной равновесной 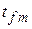; – круговая частота колебаний температуры жидкости. Остальные обозначения приведены ранее.

Приведём эту задачу к безразмерному виду, введя следующие безразмерные переменные и функции:

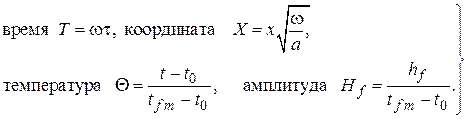
Тогда задача принимает вид

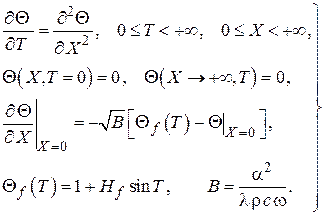
Для решения этой задачи применим операционный метод с использованием преобразования Лапласа (см. М.А Лаврентьев, Б.В. Шабат. Методы теории функций комплексного переменного. – М.: Наука, 1965. – 716 с.), в соответствии с чем определим изображения температурных функций

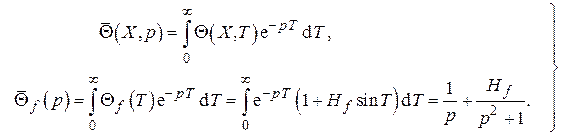
Применив процедуру преобразования Лапласа к задаче с учётом получим

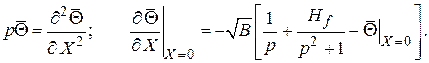
Решение дифференциального уравнения в отношении переменной X есть

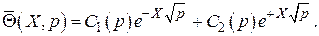
Используя граничное условие в и требование конечности решения на 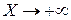, находим лапласовское изображение решения поставленной задачи

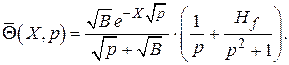
Для нахождения оригинала воспользуемся теоремой о свёртке, для чего положим

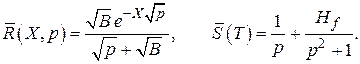
Оригиналы изображений есть (см. Градштейн, Рыжик)

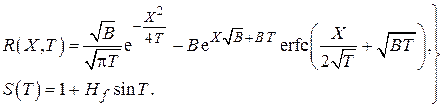
В соответствии с теоремой о свёртке оригинал 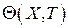представляется интегралом

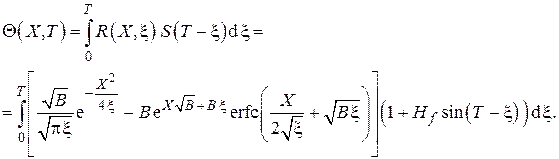
На рисунке VI.1 показаны графически результаты численного расчёта зависимости безразмерного температурного поля от времени для значения комплекса B, вычисленного в применении к массиву из алюминия, т.е. материала цилиндров поршневых двигателей внутреннего сгорания (ДВС), 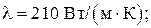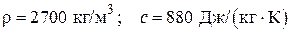при коэффициенте теплоотдачи α = 1000 Вт/(м²∙К). В расчётах было принято число оборотов четырёхтактного двигателя равным

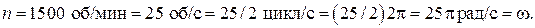
Имеем тогда

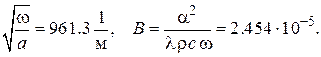
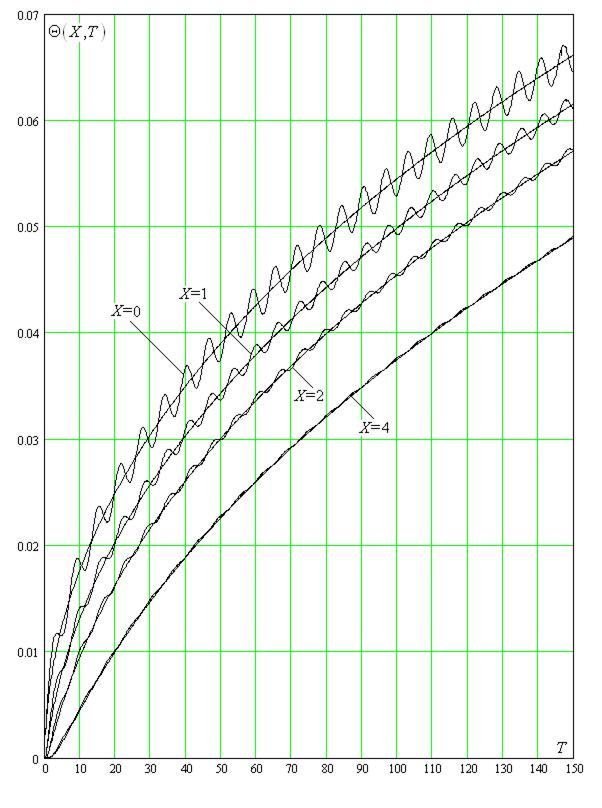
Рис. VI.1. Температурные колебания Θ(X,T) в полубесконечном одномерном массиве на различных расстояниях X от обогреваемой поверхности с гармоническим изменением температуры контактирующей с поверхностью среды.

Интервал времени по оси абсцисс (0…Т /ω=1.9 с.

Размерная координата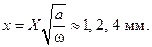

[1] Иногда их называют также “частицами” сплошной среды, которые не следует, однако, путать с обычно понимаемым термином “частица” в классической или квантовой механике.

[2] В современной научной русскоязычной литературе под жидкостью обычно понимают сплошную текучую среду (то, что раньше обозначалось словом «флюид»–fluide), при этом жидкость в обычном смысле слова называют капельной жидкостью, а газы и пары – некапельной жидкостью.

[3] Дадим здесь определения геометрических объёмных объёктов. Любое объёмное тело имеет в трёхмерном пространстве три порядковых размера 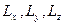. Тогда, по определению, если один из размеров, например, 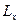, много меньше двух других, т.е. если 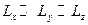, то речь идёт о пластине. Если два из линейных размеров тела много меньше третьего, т.е. если 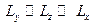, то речь идёт о стержне.