ПОЛУОГРАНИЧЕННЫХ И ОГРАНИЧЕННЫХ ОБЛАСТЯХ
Рассмотрим одномерную нестационарную задачу теплопроводности без внутренних источников тепла в бесконечном интервале 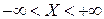
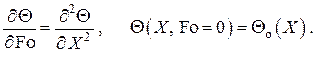
Предполагая применимость метода разделения переменных (метод Фурье), запишем общее решение задачи в виде бесконечного сходящегося ряда
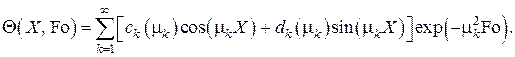
Как уже говорилось выше, в ограниченной области 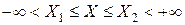 собственные значения задачи
собственные значения задачи 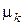 принимают бесконечный дискретный набор, определяемый заданными граничными условиями. В бесконечных пределах граничные условия отсутствуют, за исключением того, что на бесконечности искомая функция (температура) не может принимать бесконечных значений. По этой причине
принимают бесконечный дискретный набор, определяемый заданными граничными условиями. В бесконечных пределах граничные условия отсутствуют, за исключением того, что на бесконечности искомая функция (температура) не может принимать бесконечных значений. По этой причине 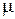 может принимать непрерывный набор значений, а сумма в должна заменяться интегралом
может принимать непрерывный набор значений, а сумма в должна заменяться интегралом
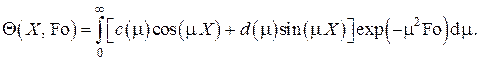
Начальное условие
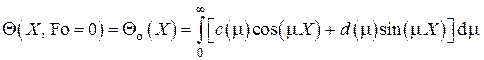
представляет собой разложение в интеграл Фурье по косинусам и синусам функции 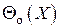 , т.е. возможны представления
, т.е. возможны представления
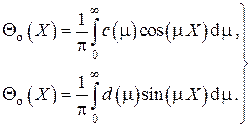
Используя интегральное косинус-представление δ-функции Дирака
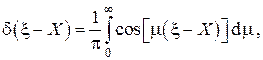
а также одно из свойств δ-функции, согласно которому
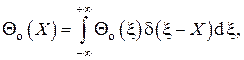
общее решение уравнения может быть записано в виде
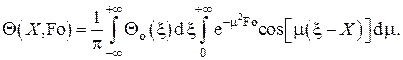
Вычислим входящий в это выражение интеграл
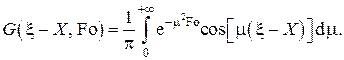
Введём обозначения
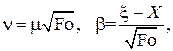
с учётом чего принимает вид
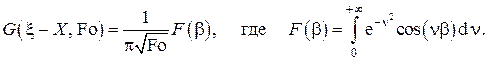
Для вычисления интеграла 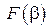 возьмём производную
возьмём производную
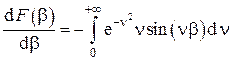
и вычислим получившийся интеграл по частям, положив
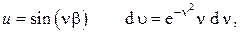
откуда
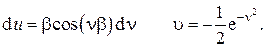
Таким образом, получаем
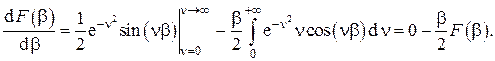
Решение этого простейшего дифференциального уравнения есть
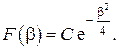
Постоянная интегрирования C в соответствии с есть
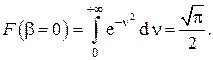
Таким образом, находим
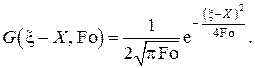
Функция 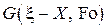 носит название функции Грина или фундаментального решения одномерного уравнения теплопроводности в неограниченной области. Непосредственным вычислением можно проверить, что функция Грина удовлетворяет дифференциальному уравнению , но не удовлетворяет начальному условию с произвольным профилем температуры вдоль оси X. Более того, дифференциальному уравнению удовлетворяют производные любого порядка от функции Грина по X и Fo, а также интегралы по тем же переменным. Функция Грина формально совпадает с функцией ошибок Гаусса и для момента времени Fo=0 представляет собой дельта-функцию Дирака, т.е. функция Грина есть решение уравнения теплопроводности для δ-образного начального распределения.. Вид функции Грина для нескольких моментов времени представлен на рис. V.1.
носит название функции Грина или фундаментального решения одномерного уравнения теплопроводности в неограниченной области. Непосредственным вычислением можно проверить, что функция Грина удовлетворяет дифференциальному уравнению , но не удовлетворяет начальному условию с произвольным профилем температуры вдоль оси X. Более того, дифференциальному уравнению удовлетворяют производные любого порядка от функции Грина по X и Fo, а также интегралы по тем же переменным. Функция Грина формально совпадает с функцией ошибок Гаусса и для момента времени Fo=0 представляет собой дельта-функцию Дирака, т.е. функция Грина есть решение уравнения теплопроводности для δ-образного начального распределения.. Вид функции Грина для нескольких моментов времени представлен на рис. V.1.
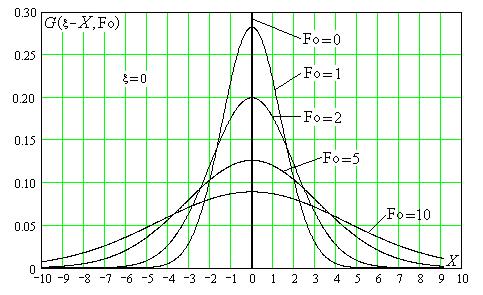
Рис.V.1. Эволюция температурного поля в одномерном бесконечном массиве при
δ–образном начальном тепловом импульсе
С помощью функции Грина решение поставленной задачи с произвольным заданным начальным профилем температуры записывается в виде
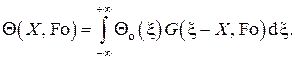
Если под одномерным пространством понимать теплоизолированный на боковой поверхности стержень бесконечной длины с постоянным поперечным сечением f , с плотностью ρ и теплоёмкостью c материала стержня, то можно вычислить энтальпию H стержня в произвольный момент времени
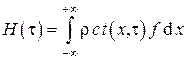
Для вычисления этого интеграла перейдём в к размерным переменным с учётом определений – . С учётом того, что
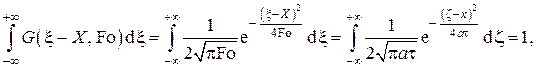
в размерной форме температурное поле в стержне будет
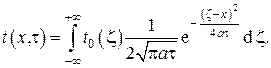
Подставляя это распределение в , имеем
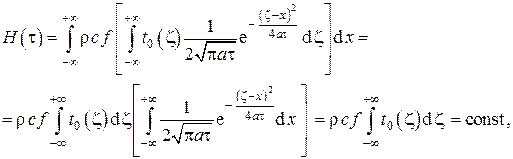
т.е., как и следовало ожидать, полная энтальпия стержня остаётся постоянной в любой момент времени в соответствии с законом сохранения энергии.
Тепловой диполь
Выберем в качестве фундаментального решения уравнения теплопроводности первую производную по координате X от функции Грина
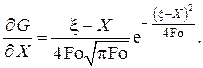
График этой функции представлен на рис. V.2.
По физическому смыслу описывает так называемый тепловой диполь, расположенный в окрестности точки ξ ( на рисунке ξ=0 ), действующий мгновенно в момент времени Fo. Тепловой диполь (по аналогии с электрическим диполем) представляет собой близко расположенные мгновенные точечные источник и сток тепла одинаковой мощности (по модулю).
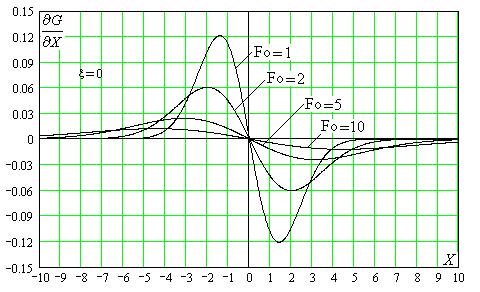
Рис.V.2. Эволюция температурного поля в одномерном бесконечном массиве
при действии мгновенного теплового диполя в плоскости X = 0
Исключительная важность функции Грина состоит в том, что с её помощью можно получить решение уравнения теплопроводности в одномерном неограниченном пространстве в самом общем случае распределённых в пространстве и во времени (не обязательно непрерывным образом) источников тепла
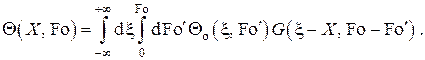
То же справедливо и для теплового диполя с заменой 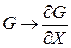 .
.
Приведём для справок одномерные температурные поля в размерной форме на бесконечной оси x при наличии точечного непрерывно действующего теплового источника мощностью 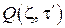 и теплового диполя той же мощности соответственно:
и теплового диполя той же мощности соответственно:
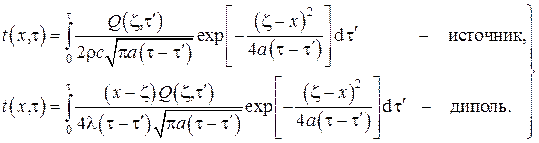
Фундаментальное решение (функция Грина) естественным образом обобщается на задачи нестационарной теплопроводности в неограниченных областях с цилиндрической 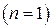 и сферической
и сферической 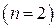 симметрией:
симметрией:
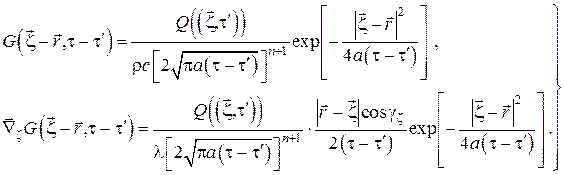
Здесь 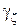 – угол между осью диполя и направлением
– угол между осью диполя и направлением 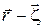 .
.
Дата добавления: 2015-12-17; просмотров: 980;
