Краевые условия для уравнения теплопроводности
Дифференциальное уравнение теплопроводности в однородных изотропных средах в терминах математической физики есть неоднородное дифференциальное уравнение в частных производных параболического типа (первого порядка по времени и второго порядка по пространственным координатам). Если внутренние тепловыделения 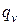 зависят от температуры
зависят от температуры
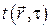 , то уравнение теплопроводности будет нелинейным, если плотность внутренних источников теплоты зависит от температуры нелинейным образом. Если же плотность внутренних источников теплоты пропорциональна первой степени температуры или не зависит от температуры, то уравнение теплопроводности будет либо линейным, либо квазилинейным, оставаясь, тем не менее, уравнением параболического типа.
, то уравнение теплопроводности будет нелинейным, если плотность внутренних источников теплоты зависит от температуры нелинейным образом. Если же плотность внутренних источников теплоты пропорциональна первой степени температуры или не зависит от температуры, то уравнение теплопроводности будет либо линейным, либо квазилинейным, оставаясь, тем не менее, уравнением параболического типа.
Как бы то ни было, любое дифференциальное уравнение может дать однозначное решение только если заданы условия однозначности. В случае дифференциального уравнения параболического типа должно быть задано начальное условие
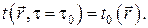
Что касается граничных условий, то-есть условий теплообмена на границе рассматриваемого объёма с окружающей (контактирующей с ним) средой, то здесь имеют место несколько (а именно, четыре) возможностей, каждая из которых характеризует тот или иной тип теплового взаимодействия с внешней средой. Эти возможности обычно нумеруются римскими цифрами. Перечислим их.
I. Граничные условия I рода
В этом случае задаётся распределение температур на физической границе рассматриваемого объёма, т.е. задаётся функция координат поверхности и времени
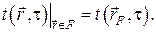
II. Граничные условия II рода
Задаётся плотность теплового потока на границе рассматриваемого тела, что позволяет записать
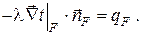
Такие граничные условия обычно имеют место при решении задач теплопроводности в твёрдых телах с теплообменом излучением на границах. Чаще всего такие задачи возникают при решении задач в металлургической теплотехнике, в астрофизике и т.д.
III. Граничные условия III рода
Граничные условия III рода наиболее распространены при решении задач теплопроводности в энергетике, в металлургии и в химической технологии.
Граничные условия III рода описывают в математической форме условия теплообмена внешней поверхности твёрдого тела с контактирующей с ним жидкостью или газом, т.е. со средами, допускающими конвективные движения с перемешиванием.
Математическая формулировка граничных условий III рода базируется на гипотезе (законе) Ньютона-Рихмана, согласно которой тепловой поток с поверхности к омывающей её жидкости пропорционален разности температур, т.е.
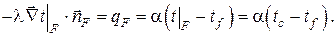
Здесь 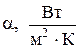 есть по определению коэффициент теплоотдачи, представляющий собой количество теплоты, снимаемое в единицу времени с единичной поверхности при единичной разности температур.
есть по определению коэффициент теплоотдачи, представляющий собой количество теплоты, снимаемое в единицу времени с единичной поверхности при единичной разности температур.
Экспериментальное обоснование гипотезы Ньютона-Рихмана состоит в том, что, как показывают экспериментальные исследования, количество теплоты, снимаемое с поверхности твёрдого тела, прямо пропорционально поверхности и разности температур поверхности и жидкости вдали от неё (как говорят, в ядре потока). Нахождение величины коэффициента теплоотдачи 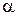 является задачей экспериментальной теплофизики (вплоть до теоретических исследований) и будет обсуждено в дальнейшем изложении курса. В задачах теплопроводности значения коэффициентов теплоотдачи будут считаться заданными и постоянными.
является задачей экспериментальной теплофизики (вплоть до теоретических исследований) и будет обсуждено в дальнейшем изложении курса. В задачах теплопроводности значения коэффициентов теплоотдачи будут считаться заданными и постоянными.
IV. Граничные условия IV рода
Граничные условия IV рода задают условия теплообмена на границе контакта твёрдых поверхностей. В частности, если контакт твёрдых поверхностей неидеален, то на границе их контакта в математическом смысле будет иметь место скачок температуры 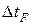 , а при наличии тепловыделения на поверхностях контакта будет иметь место дополнительный поток тепла
, а при наличии тепловыделения на поверхностях контакта будет иметь место дополнительный поток тепла 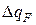 . В этом случае граничные условия математически запишутся в виде
. В этом случае граничные условия математически запишутся в виде
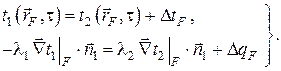
Дата добавления: 2015-12-17; просмотров: 6594;
