Глава II. ТЕОРИЯ ТЕПЛОПРОВОДНОСТИ

Механизмы теплопроводности в различных сплошных средах

По определению под теплопроводностью (conduction проводимость) понимается передача энергии в сплошной среде без видимых макроскопических перемещений. Объяснить механизм теплопроводности можно только с привлечением представлений молекулярно-кинетической теории (МКТ) и физической кинетики. При этом механизмы теплопроводности на микроскопическом уровне различны и зависят от агрегатного состояния вещества, типа кристаллической решётки, наличия свободных электронов и т.д.

Обсудим вкратце каждый из этих механизмов.

Газы

Теплопроводность в газах в состояниях, близких к идеальному, обусловлена непосредственными столкновениями отдельных электрически нейтральных молекул.

Замечания:

1. Предположение об идеальности газа в строгом термодинамическом смысле в применении к явлениям теплопроводности является некорректным, так как молекулы идеального газа, ассоциируемые с математическими точками, по определению не могут взаимодействовать друг с другом, т.е. обмениваться энергиями и импульсами. При описании процессов переноса в газах нельзя пренебрегать геометрическими размерами микрочастиц.

2. Строго говоря, под столкновениями следует понимать квантово-механическое взаимодействие молекул на расстояниях порядка и меньше де-бройлевской длины волны относительного движения молекул. Впрочем, качественная картина взаимодействий не зависит от классического или квантового подхода к описанию акта взаимодействия.

Как известно из теории столкновений при соударении двух тел, то из тел, которое имело бòльшую скорость (энергию), замедляется (теряет энергию), а более медленно движущееся тело ускоряется (приобретает энергию). И поскольку абсолютная температура газа 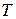пропорциональна средней кинетической энергии поступательного движения молекул, то в среднем участки газа с более высокой температурой (средней кинетической энергией) будут охлаждаться, а участки с более низкой температурой будут нагреваться.

Кристаллы

Кристаллы (имеются в виду монокристаллы) представляют собой упорядоченную структуру, составленную из ионов, хаотически колеблющихся около фиксированных положений равновесия, называемых узлами кристаллической решётки. Ионы кристалла связаны между собой силами электростатического и/или обменного (квантовомеханического) взаимодействий (водородная, ковалентная, ионная связь и др.). Кроме ионов в кристалле могут присутствовать свободные электроны (металлы, полупроводники) либо так называемые «дырки». Свободные электроны в кристалле образуют так называемый «электронный газ», аналогичный обычному газу за исключением того, что в электронном газе нельзя пренебрегать взаимодействием между частицами. Это вызвано тем, что сила взаимодействия между электронейтральными молекулами обусловлена дипольными моментами (собственными или индуцированными) и обратно пропорциональна кубу расстояния между ними, в то время как в случае заряженных частиц (электроны) сила взаимодействия обратно пропорциональна квадрату расстояния между ними (Кулон). Интенсивность колебаний ионов кристаллической решётки пропорциональна абсолютной температуре. Вследствие сравнительно интенсивной связи между ионами кристалла их колебания не являются независимыми. Эти колебания внутри кристалла конечных размеров образуют систему стоячих волн с дискретным набором частот. Каждая из мод колебаний ассоциируется с некоторой «квазичастицей», названной фононом. Таким образом квантовомеханический подход к описанию коллективных колебаний в кристалле приводит к понятию так называемого «фононного газа» и позволяет рассматривать процесс теплопроводности в кристалле как процесс теплопроводности в газе (конечно, со специфическими отличиями).

При комнатных температурах электронный механизм теплопроводности в металлах преобладает над фононным, однако при низких («гелиевых») температурах электронный газ «вырождается» и преобладающим становится фононный механизм.

В случае поликристаллических материалов механизм теплопроводности остаётся качественно тем же, количественное же описание требует при этом статистического усреднения по функциям распределения по ориентациям и размерам отдельных кристаллов и различных дефектов кристаллических решёток.

Жидкости

По современным представлениям жидкость представляет собой промежуточное состояние между газом и кристаллом. В жидкости хаотическим образом молекулы газа группируются в малые, но макроскопические кристаллы, которые с частотой в несколько сотен тысяч герц разрушаются и вновь образуются. При этом время жизни кристаллов уменьшается с повышением температуры и при температуре кипения время жизни кристаллов падает до нуля. В соответствии с этими представлениями в жидкостях имеют место все три механизма теплопроводности – фононный, электронный и «газовый».

Аморфные тела (стекло, смола, органика, живые ткани) представляют собой неньютоновские жидкости с аномально большой вязкостью, поэтому в таких средах теплопроводность осуществляется в основном распространением колебательных движений макромолекул и их агрегатов.

Закон Био-Фурье

Основными задачами теории теплообмена являются нахождение полей температур 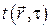в сплошных средах (химическая технология, металлургия и т.д.) и тепловых потоков 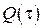(отопление и т.д.). Классическая термодинамика, в частности II начало, утверждает, что обмен энергией в форме теплоты возможен только при наличии пространственной неоднородности температурного поля. Это позволяет записать логическую цепочку

следствие причина

тепловой поток пространственная неоднородность температур

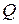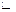
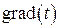, Вт , К/м

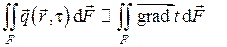
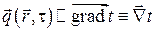
В соответствии с II началом термодинамики математически зависимость плотности теплового потока от неоднородности температурного поля (градиента температур) записывается в виде векторной функции 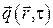от векторного аргумента 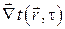, т.е.

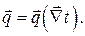
Эта зависимость в рамках термодинамики (теории теплопроводности в приближении локального равновесия) не может быть установлена строго математически. Для этой цели прибегают либо к эксперименту, либо к теоретическому описанию с использованием различных модельных теорий. На практике в подавляющем большинстве случаев прибегают к экспериментальным исследованиям. Это в полной мере касается исследований в области теплообмена во всех его проявлениях. Обработка экспериментальных данных представляет собой всегда довольно сложную задачу и при корректном подходе приводит к процедуре последовательных приближений. Эти последовательные приближения с математической точки зрения представляют собой поиск зависимостей в виде разложений в обобщённый ряд Тейлора (Маклорена) для непериодических процессов, либо в обобщённый ряд Фурье в случае периодических процессов.

Итак, запишем ряд Тейлора векторной функции от векторного аргумента 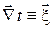. Для сокращения записи и для лучшего обозрения представим векторы в виде матриц-столбцов, в частности

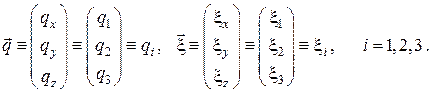
Тогда

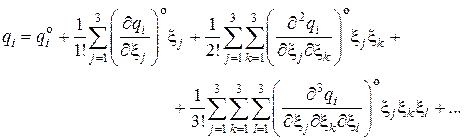
Здесь верхний индекс указывает на то, что функция и её производные вычисляются при значениях аргумента 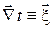, равных нулю, т.е. при однородном распределении температур.

Обратимся теперь к физике. Второе начало термодинамики в формулировке Клаузиуса требует, чтобы функция и все её производные чётного порядка в нуле исчезали, т.е.

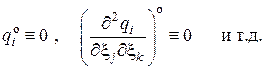
Таким образом, в линейном приближении по градиенту температурного поля имеем

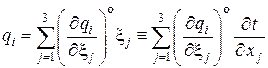
Частные производные 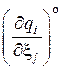представляют собой квадратную матрицу. В связи с этим введём обозначение

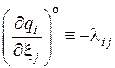
таким образом, что

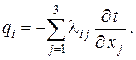
Квадратная матрица 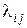носит название матрицы коэффициентов теплопроводности. Эта матрица обладает двумя самыми общими свойствами:

а) симметричность ;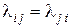

б) положительная определённость.

Симметричность матрицы коэффициентов теплопроводности обусловлена микроскопической обратимостью, т.е. независимостью элементарных процессов взаимодействия микрочастиц от направления течения времени; положительная определённость является следствием второго начала термодинамики.

Численные значения элементов матрицы коэффициентов теплопроводности в большинстве своём берутся из экспериментов, в простейших случаях они могут быть вычислены теоретически с использованием методов молекулярно-кинетической теории.

Вид матрицы 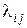зависит также от свойств симметрии среды. В частности, в случае изотропных сред (газы, жидкости, поликристаллические среды) матрица коэффициентов теплопроводности вырождается в скаляр, т.е.

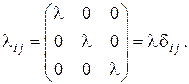
В этом случае выражение упрощается и принимает вид

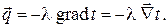
Такая линейная зависимость плотности теплового потока от градиента температурного поля в приложении к изотропным средам носит название закона Био-Фурье.

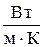Коэффициент теплопроводности имеет размерность и представляет собой количество теплоты, проходящей через поверхность единичной площади при единичном градиенте температур в направлении нормали к поверхности.

В соответствии с численными значениями коэффициента теплопроводности в теплотехнике различают так называемые теплоизоляционные материалы и теплопроводные материалы, используемые для увеличения теплосъёма в различных установках и устройствах с интенсивным выделением тепла в рабочих режимах функционирования.

В качестве теплоизоляторов используются вещества и материалы с коэффициентами теплопроводности, не превышающими 0.05…1.0 Вт/(м·К). Примерами таких веществ являются практически все газы, пористые материалы, полимеры, дерево и т.д.).

Наиболее теплопроводными естественными материалами являются металлы, среди которых выделяются такие из них, как серебро Ag , медь Cu 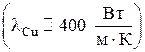и алюминий Al . Коэффициент теплопроводности наиболее распространённых технических сталей составляет величину порядка .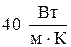

Дифференциальное уравнение теплопроводности в неподвижных однородных изотропных средах

Основной задачей теории теплопередачи является вычисление температурных полей (технология) и тепловых потоков (отопление и т.д.).

Аналитическое описание процессов теплопроводности в твёрдых телах осуществляется с использованием закона сохранения полной энергии (I начала термодинамики) в локальной формулировке и эмпирического закона Био-Фурье. С этой целью рассмотрим неподвижный объём V, ограниченный поверхностью F,заполненный однородной сплошной средой с постоянными теплофизическими характеристиками – плотностью ρ, теплоёмкостью c и теплопроводностью λ – (см. рис. II.1).

Первое начало термодинамики для неподвижных термодинамических систем в дифференциальной форме записывается в виде

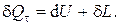
Здесь U, Дж – внутренняя энергия тела; L, Дж – работа, совершаемая телом над внешними телами; Q_τ, Дж – теплота, подведённая к телу.

Неполный дифференциал работы в общем случае представляется суммой частных дифференциалов, каждое слагаемое в которой даёт малое количество работы, обусловленной различными механизмами: изменение объёма, деформация, поверхностное натяжение, протекание электрических зарядов, электрическая поляризация, намагничение. Запишем для справки дифференциал работы в общем случае, представив слагаемые в вышеперечисленном порядке, используя общепринятые обозначения,

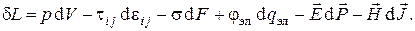
В случае несжимаемых недеформируемых сред первые три слагаемых в правой части этого выражения исчезают, и остаются только члены, связанные с электрическими и магнитными воздействиями.

Отнесём I начало термодинамики к единице времени и запишем результат с учётом определения теплового потока в виде

Внутренняя энергия недеформируемого твёрдого тела в приближении локального равновесия определится суммированием (интегрированием) внутренних энергий физически бесконечно малых объёмов, на которые мысленно разбивается рассматриваемое тело

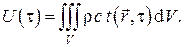
Скорость изменения внутренней энергии

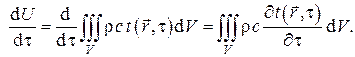
Здесь было учтено, что при постоянном объёме V операции дифференцирования по времени и интегрирования по пространственным координатам коммутируют, а полная производная по времени заменяется частной производной по времени от температуры, являющейся функцией не только времени, но и пространственных координат.

Тепловой поток Q, Вт, подводимый к рассматриваемому объёму V, обусловлен в общем случае двумя факторами: потоком тепла через ограничивающую объём поверхность – 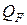и тепловыделениями внутри объёма – 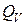, причинами которых могут быть химические реакции, ядерные реакции, индукционные токи и др.. В перечень внутренних источников тепла включаются также тепловые эффекты, связанные с электрическими и магнитными воздействиями – последние три слагаемых в . В этом случае представляется в виде

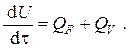
Вычисление мощности внутренних источников тепла представляет отдельную задачу, выходящую за рамки рассматриваемого метода. В самом общем случае можно лишь утверждать, что при неоднородном пространственном тепловыделении (теплопоглощении) внутри объёма мощность внутренних источников тепла может быть представлена тройным интегралом

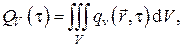
где 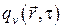с размерностью Вт/м³ представляет собой плотность внутренних источников теплоты.

Тепловой поток в рассматриваемый объём через ограничивающую поверхность записывается в общем случае в виде поверхностного интеграла второго рода

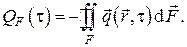
Здесь знак «–» выбран потому, что внутренняя энергия тела будет возрастать тогда, когда тепловой поток направлен внутрь объёма, а нормаль к элементу замкнутой поверхности, по определению в математике, направлена наружу.

Итак, в интегральном виде баланс энергии (в данном случае теплоты) принимает вид

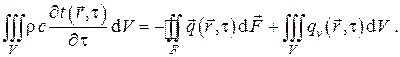
Используя теорему Остроградского-Гаусса и произвольность рассматриваемого объёма, получаем баланс теплоты в локальной (дифференциальной) форме

Используя приближение в виде закона Био-Фурье , получаем дифференциальное уравнение теплопроводности в неподвижной однородной и изотропной среде (опускаем обозначения независимых пространственных и временнóй переменных)

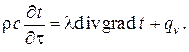
Обычно это дифференциальное уравнение записывается в виде

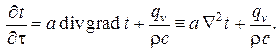
Здесь комплекс

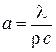
с размерностью м²/с носит название коэффициента температуропроводности.