Метод неравновесной термодинамики. Гипотеза локального равновесия
Лекция теплообмен
Теплообмен (теплопередача) есть, по определению, обмен энергией в форме теплоты, т.е. на микроскопическом уровне, в неизотермических условиях.
Движущей силой теплообмена является пространственная неоднородность температур.
Классическая теория теплопередачи оперирует терминами и понятиями макроскопической физики и в этом смысле представляет собой раздел классической термодинамики, обобщённой на необратимые процессы распространения энергии в неизотермических условиях. Строго говоря, это обобщение неправомерно, так как такие макроскопические понятия, как температура, плотность, давление, концентрации химических элементов определены только для равновесных состояний макроскопических систем. В связи с этим сделаем отступление в область строгих, абстрактных понятий термодинамики и возможности применения макроскопических, термодинамических параметров состояния к неравновесным системам.
Принципы и методы классической термодинамики являются мощным аппаратом исследования статических свойств веществ и квазистатических процессов изменения их состояния. Второе начало термодинамики, т.е. закон возрастания энтропии, позволяет также судить о направленности реальных процессов в природе и исследовать вопросы устойчивости равновесных состояний термодинамических систем. Всё это является чрезвычайно полезным для конструирования тепловых машин и анализа их работы с точки зрения максимальной термодинамической эффективности, а также для повышения эффективности многих технологических процессов. Однако следует иметь в виду, что несмотря на бесспорность и общий характер принципов, на которые опирается классическая термодинамика, её возможности тем не менее ограничены. Для лучшего понимания сути этих ограничений рассмотрим вкратце основные положения классической, равновесной термодинамики с критической точки зрения.
Классическая термодинамика имеет дело с макроскопическими объектами (телами, системами), причём никаких моделей относительно внутреннего (т.е. микроскопического) строения вещества ей принципиально не требуется. Само определение «макроскопичности» термодинамической системы в рамках термодинамики не может быть дано. Обычно интуитивно вещество (или поле), составляющее термодинамическую систему, представляется сплошной средой (по крайней мере, в пределах фаз), но это никак не сказывается на описательном уровне методами термодинамики.
Макроскопические системы, рассматриваемые методами классической термодинамики, предполагаются всегда находящимися в состоянии теплового равновесия, как внутреннего, так и с внешней средой, если система каким-либо образом с ней взаимодействует. Образно говоря, классическая термодинамика имеет дело с «мёртвыми» системами, и по этой причине правильнее было бы называть ее термостатикой. Состояние равновесной термодинамической системы описывается конечным (как правило, небольшим) количеством макроскопических параметров, значение каждого из которых может быть количественно измерено тем или иным макроскопическим прибором. Существенным является то, что каждый из параметров состояния всегда имеет отношение только ко всей системе в целом. Таковы, например, масса системы М, объём V, давление р, температура Т и т.д. Тот факт, что вместо экстенсивных параметров, таких как объём, внутренняя энергия, энтальпия, энтропия и проч., часто вводятся в рассмотрение их удельные величины или плотности, не меняет сути дела. Всегда подразумевается, что удельные параметры одинаковы по всему объёму системы.
В классической термодинамике отсутствует понятие физического времени. Оно и понятно, так как рассматриваемые ею системы «мертвы». Если время и появляется в каких-либо уравнениях, то лишь как некий параметр в математическом смысле этого слова, позволяющий отличить одно равновесное состояние от другого. Это связано с тем, что равновесная термодинамика изучает не реальные процессы изменения состояния термодинамических систем, а только последовательности равновесных состояний. Строго говоря, такое возможно лишь при бесконечно медленном изменении внешних воздействий на систему.
Несмотря на перечисленные выше ограничения, классическая термодинамика удовлетворительно описывает весьма широкий круг явлений и процессов в весьма широких пространственных и временны́х масштабах: от капель тумана до газопылевых туманностей, от неподвижного газа до скоростей истечения из ракетных сопл, от обычного газа до поля электромагнитного излучения в полости.
И тем не менее, возможности классической, равновесной термодинамики существенно ограничены. Самым главным её недостатком является невозможность исследования неравновесных состояний макроскопических систем и их перехода из одного состояния в другое через неравновесные состояния, а также процессов переноса, то есть процессов распространения той или иной субстанции (массы, энергии, импульса и т.д.) из одной части системы в другую. Этими вопросами занимается так называемая неравновесная термодинамика или термодинамика необратимых процессов (ТНП).
Метод неравновесной термодинамики. Гипотеза локального равновесия
Неравновесная термодинамика как самостоятельная научная дисциплина берёт своё начало с работы Ларса Онсагера 1931 года [1], хотя многие задачи, имеющие к ней отношение, были рассмотрены ещё в XIX веке, в частности, были установлены феноменологические законы Ома, Био–Фурье, Фика и др., были известны перекрёстные эффекты (термодиффузия, бародиффузия, эффект Пельтье и др.), а также уравнения переноса (теплопроводности, Навье–Стокса). Однако до 1931 года все эти задачи носили разрозненный характер, не выводились из общего принципа, не допускали их обобщения и установления взаимного влияния эффектов.
Метод неравновесной термодинамики, как и метод классической термодинамики, остаётся феноменологическим, то есть описание систем предполагается в терминах макроскопических параметров, таких как давление, температура, плотность, концентрация и т.д. Однако так как объектом исследования неравновесной термодинамики является неравновесная термодинамическая система, понятия параметров должны быть уточнены и чётко обозначены границы применимости макроскопических параметров для неравновесных систем, что, понятно, не может быть сделано в рамках самой термодинамики. Правомерность использования обычных интенсивных макроскопических параметров для описания поведения неравновесных систем постулируется так называемой гипотезой локального равновесия, согласно которой неравновесная система, рассматриваемая в приближении сплошной среды, может быть мысленно разбита на достаточно большое число малых подсистем, взаимодействующих друг с другом, каждая из которых может с достаточной степенью точности считаться внутренне равновесной, хотя равновесия даже между соседними подсистемами может не быть. При этом следует иметь в виду, что разбиение неравновесной системы на малые подсистемы не может быть даже теоретически бесконечным, так как каждый из малых объёмов должен содержать достаточно большое число микрочастиц, чтобы к нему можно было применять термодинамические методы. Такие малые, но макроскопические объёмы обычно называют физически бесконечно малыми[1]. Единственным «оправданием» справедливости гипотезы локального равновесия может служить удовлетворительное совпадение полученных на её основе результатов с экспериментами.
Гипотеза локального равновесия в совокупности с приближением сплошной среды позволяет вводить в рассмотрение математические поля интенсивных макроскопических переменных и использовать для их описания аппарат теории дифференциальных уравнений в частных производных. Таким образом, неравновесные системы можно рассматривать как системы с бесконечным числом термодинамических степеней свободы.
Основные понятия, определения и обозначения теории теплообмена
– Количество теплоты 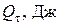 – количество энергии в форме теплоты, прошедшее через поверхность
– количество энергии в форме теплоты, прошедшее через поверхность  за время
за время 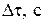 .
.
– Тепловой поток  – количество энергии в форме теплоты, прошедшее через поверхность
– количество энергии в форме теплоты, прошедшее через поверхность  за единицу времени
за единицу времени 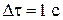 .
.
– Плотность теплового потока  , формально определяемая через поверхностный интеграл II рода таким образом, что
, формально определяемая через поверхностный интеграл II рода таким образом, что
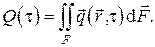
В развёрнутой записи в декартовых координатах имеем
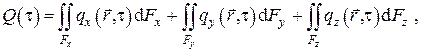
откуда по определению
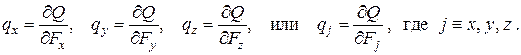
– Температурное поле 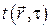 – скалярная однозначная функция, задающая значение температуры в момент времени
– скалярная однозначная функция, задающая значение температуры в момент времени 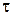 в окрестности точки
в окрестности точки 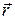 пространства, занятого сплошной средой. С физической точки зрения температура может принимать значения в пределах
пространства, занятого сплошной средой. С физической точки зрения температура может принимать значения в пределах 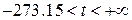 .
.
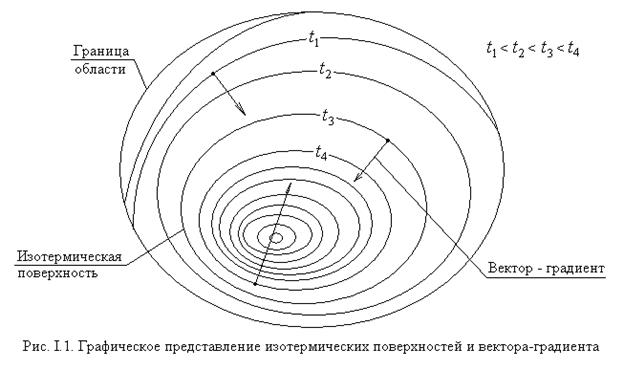
– Изотермические поверхности – кусочно-непрерывные поверхности в пространстве, занятом сплошной средой, на которых температура в момент времени 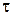 имеет одинаковое значение. Уравнение изотермической поверхности задаётся соотношением
имеет одинаковое значение. Уравнение изотермической поверхности задаётся соотношением 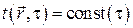 . Изотермические поверхности обладают двумя самыми общими свойствами:
. Изотермические поверхности обладают двумя самыми общими свойствами:
- различные изотермические поверхности не пересекаются;
- изотермические поверхности замкнуты, либо опираются на границы области, занятой сплошной средой.
– Градиент температурного поля  – векторное поле, задающее в каждой точке пространства, занятого сплошной средой, максимальную скорость пространственного изменения температуры в данный момент времени. В математическом анализе принимается, что вектор-градиент
– векторное поле, задающее в каждой точке пространства, занятого сплошной средой, максимальную скорость пространственного изменения температуры в данный момент времени. В математическом анализе принимается, что вектор-градиент  направлен в сторону увеличения температуры нормально к изотермической поверхности в данной точке пространства (см. рис. I.1).
направлен в сторону увеличения температуры нормально к изотермической поверхности в данной точке пространства (см. рис. I.1).
Виды теплообмена
В практике теплообмена уверенно разделяются три его вида, а именно:
I. Теплопроводность
II. Конвективный теплообмен
III. Тепловое излучение
Следует иметь в виду, что в общем случае в процессах теплообмена имеют место все три его вида. Мы будем изучать каждый из них в отдельности. Дадим вкратце определение каждого из перечисленных видов теплообмена, оставив подробное их обсуждение на дальнейшее.
Теплопроводность– микроскопическая форма обмена энергией между телами или участками одного и того же тела с различными температурами (не связанной ни с какими видимыми формами движения). Может иметь место в любых сплошных средах.
Конвективный теплообмен– обмен энергией, связанный с переносом внутренней энергии (энтальпии) макроскопическими объёмами текучей сплошной среды на макроскопические расстояния. Может иметь место в текучих сплошных средах[2] (жидкостях, газах, парах).
Тепловое излучение – обмен энергией между телами с различными температурами с помощью электромагнитных волн (фотонов) со сплошным энергетическим спектром с максимумом в области миллиметровых волн. Может иметь место во всех сплошных средах и в вакууме.
Дата добавления: 2015-12-17; просмотров: 1727;
