ДЕТЕРМИНИРОВАННЫЕ СИГНАЛЫ 11 страница

Корреляционная функция комплексной огибающей рассматри­ваемого сигнала получается подстановкой в исходное выражение

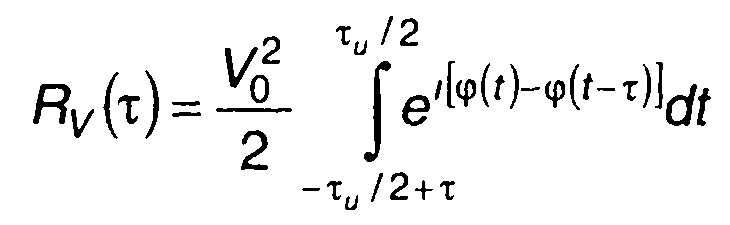(11.74)

фазы, описываемой (11.67),

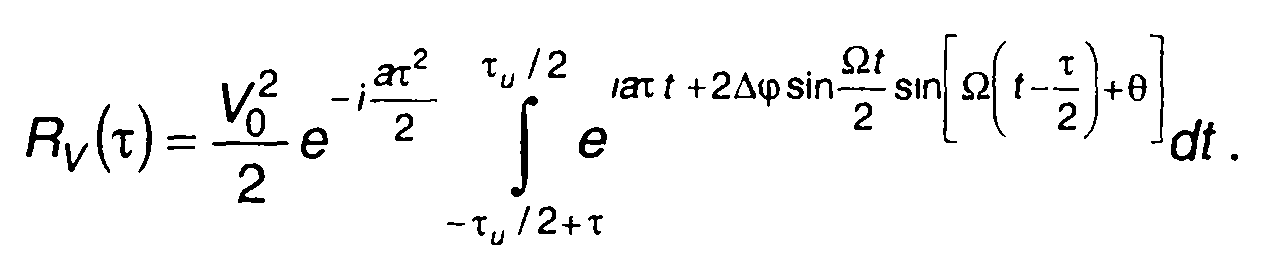(11.75)

Используя разложение (11.69), запишем

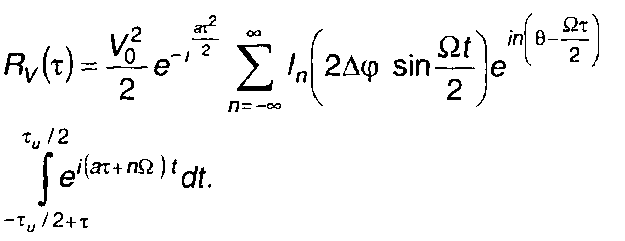(11.76)

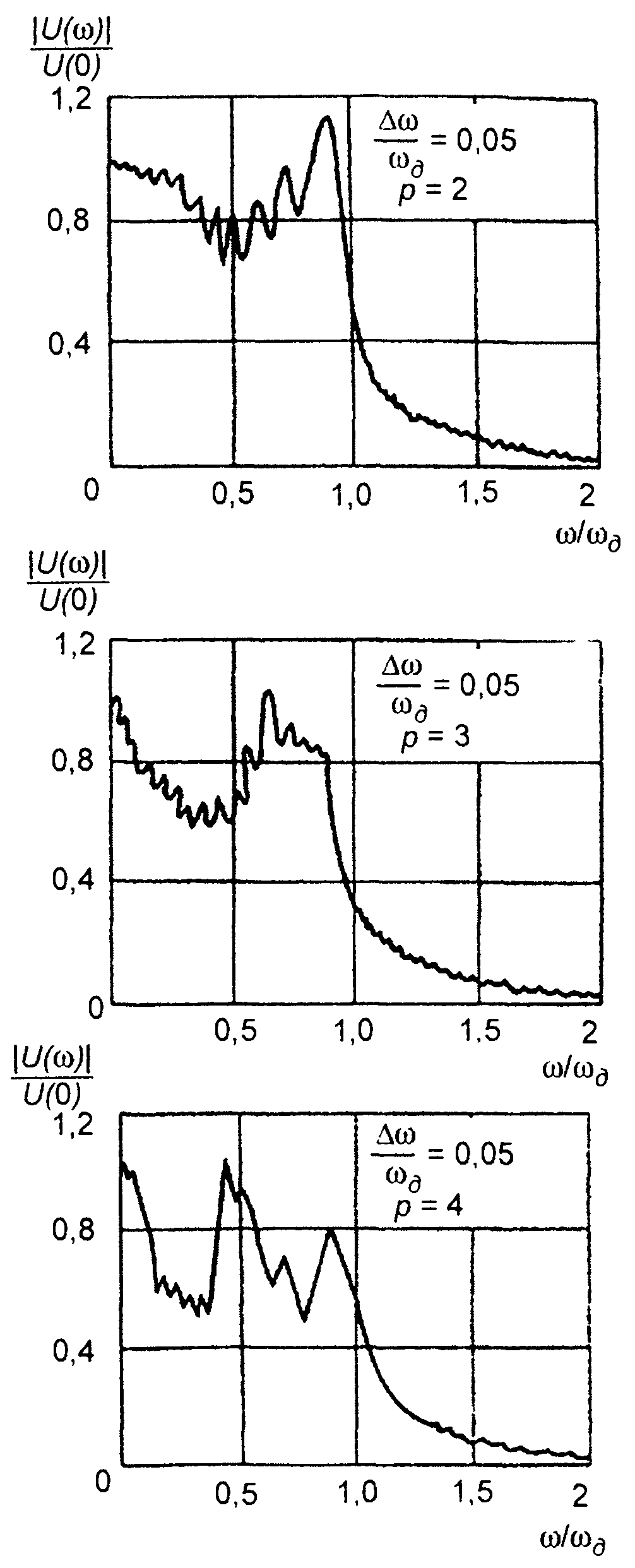
Рис. 11.11

После интегрирования в (11.76) получим при т > О

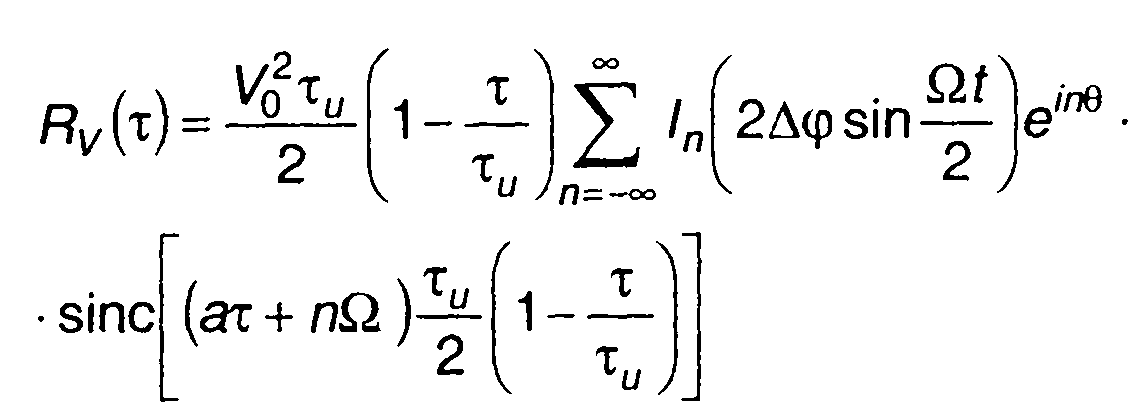(11.77)

При ∆ω = 0 (искажения отсутствуют) выражение (11.77) совпа­дает с выражением для корреляционной функции комплексной оги­бающей ЛЧМ сигнала.

При малых значениях т (т<< т_u), что при больших значениях ба­зы сигнала В практически не накладывает ограничений на рас­сматриваемый интервал т, можно принять

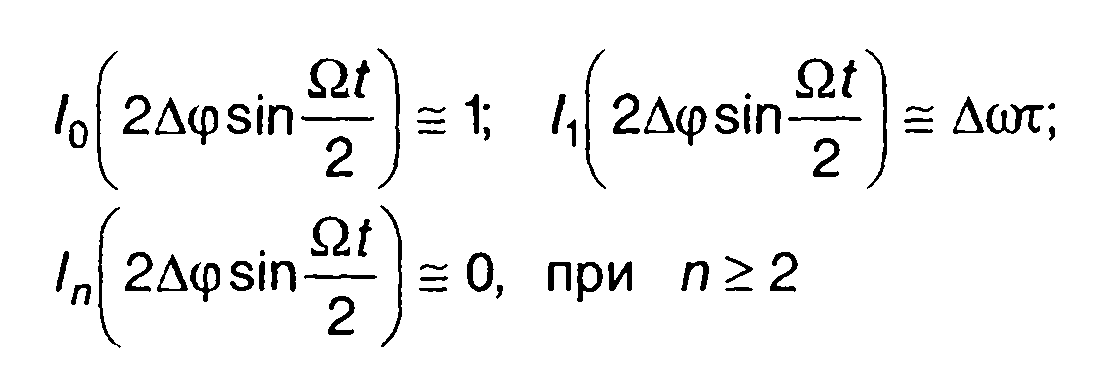
Выражение для корреляционной функции запишем в виде

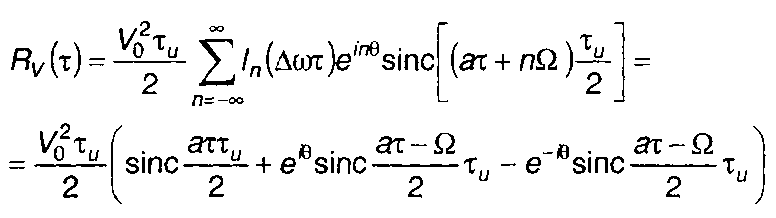(11.78)

или

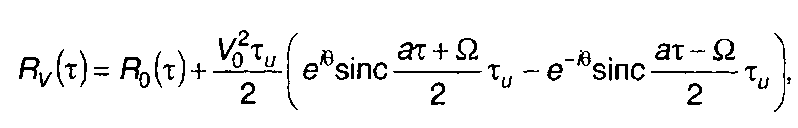(11.79)

где R₀(т) - корреляционная функция комплексной огибающей ЛЧМ сигнала (без искажений).

Графики модуля корреляционной функции комплексной оги­бающей сигнала при Θ = 0 и различных значениях ∆ω и р приве­дены на рис. 11.12. Анализ графиков показывает, что искажение закона ЧМ приводит к увеличению р-го бокового лепестка

корреляционной функции. Этот рост заметен только, начиная с некоторого (порогового) значения ∆ω.

Практический интерес представляет взаимная корреляционная функция комплексных огибающих ЛЧМ сигнала и ЛЧМ сигнала с искажением закона модуляции. Она позволяет оценить огибаю­щую сигнала на выходе фильтра, согласованного с ЛЧМ сигналом при искажении закона модуляции. Выражение для взаимной корре­ляционной функции комплексных огибающих ЛЧМ сигнала без ис­кажения закона модуляции и сигнала с искажением может быть записано в виде

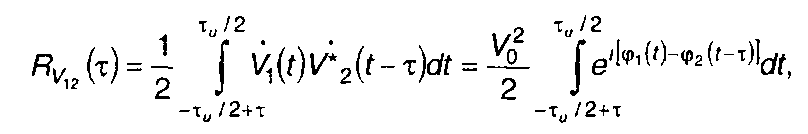(11.80)

где V₁(t) = V₀e^iφ1(t); V₂(t) = V₀e^iφ2(t) - комплексные огибающие сиг­налов с искажением и без искажения закона модуляции.

Фазы сигналов с искажением и без искажения закона модуляции описываются (11.67) и (11.4).

При 0 = 0

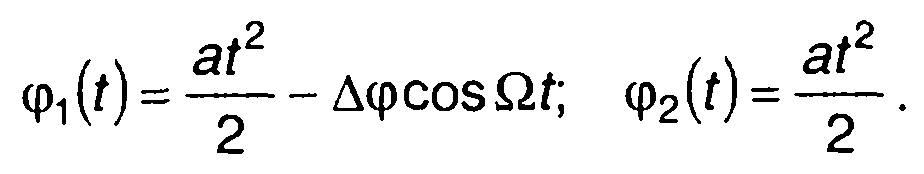(11.81)

Подставляя (11.81) в (11.80), получаем

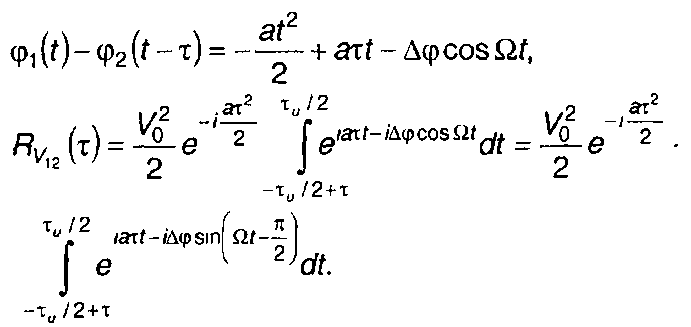(11.82)

Используя (11.69), выражение для Rv₁₂(т) представляем в виде

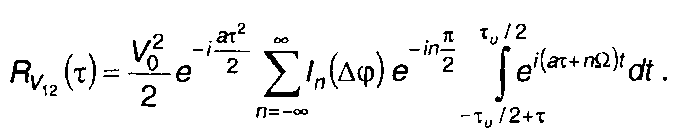(11.83)

Из (11.83) для т > 0 найдем

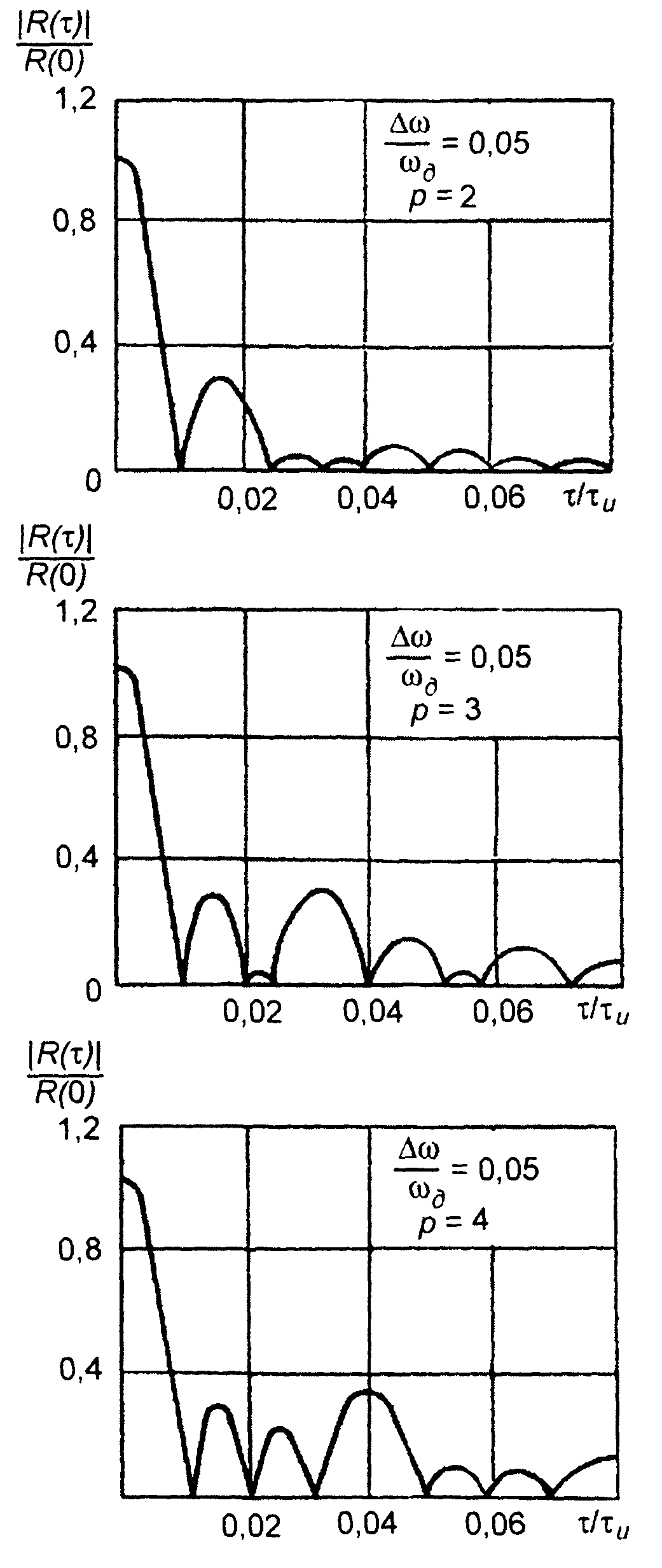
Рис. 11.12

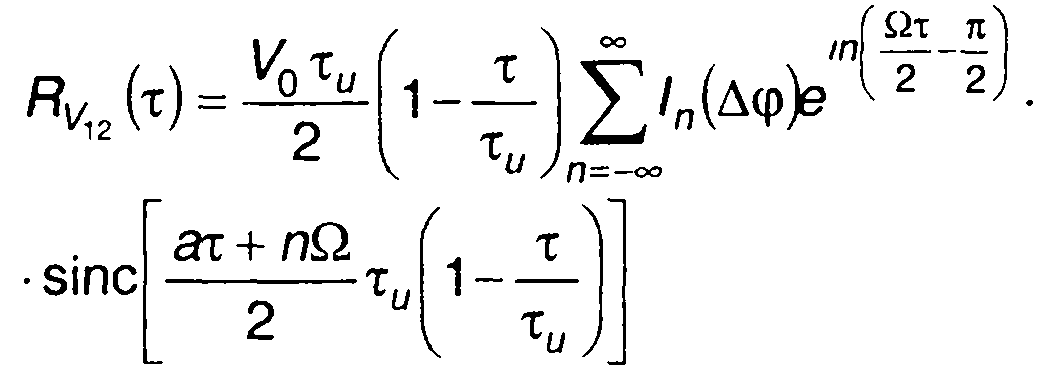(11.84)

При τ << τ_и получим

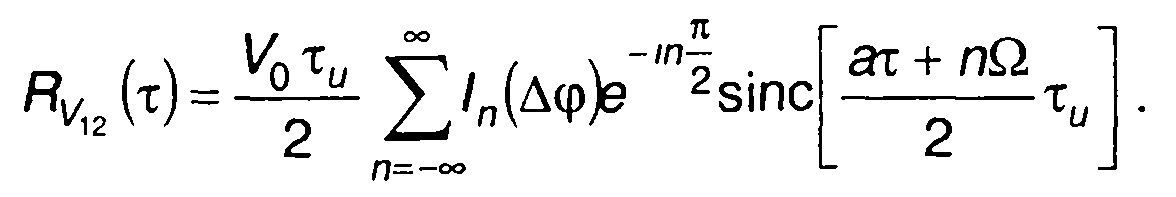(11.85)

Подставив в (11.85)

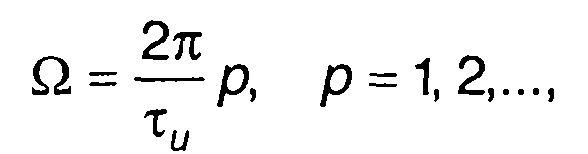(11.86)

запишем

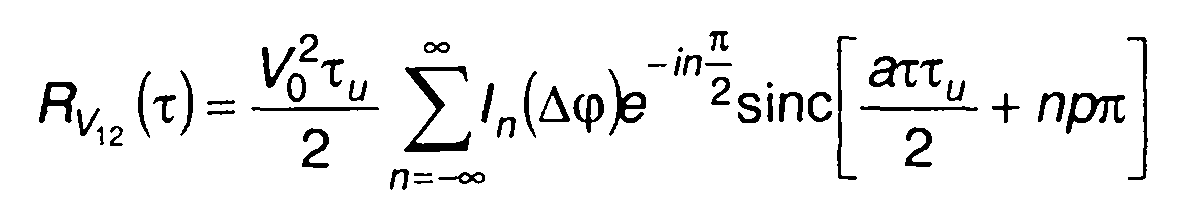(11.87)

или

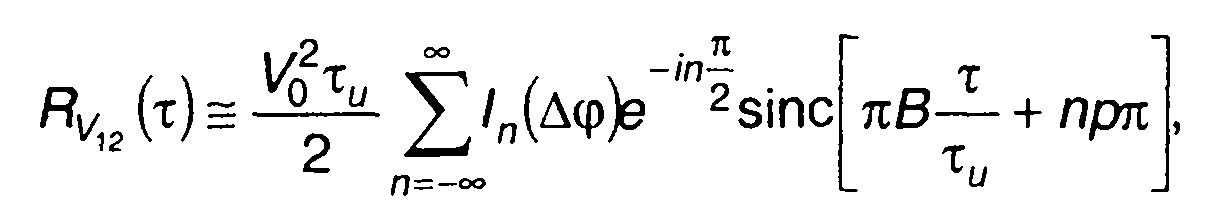(11.88)

где

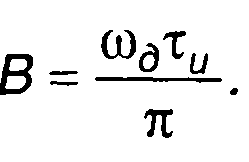
При малых искажениях (∆φ << 1) можно принять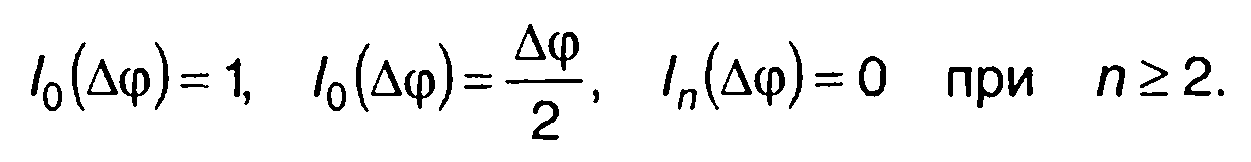

В этом случае (11.88) запишется в виде

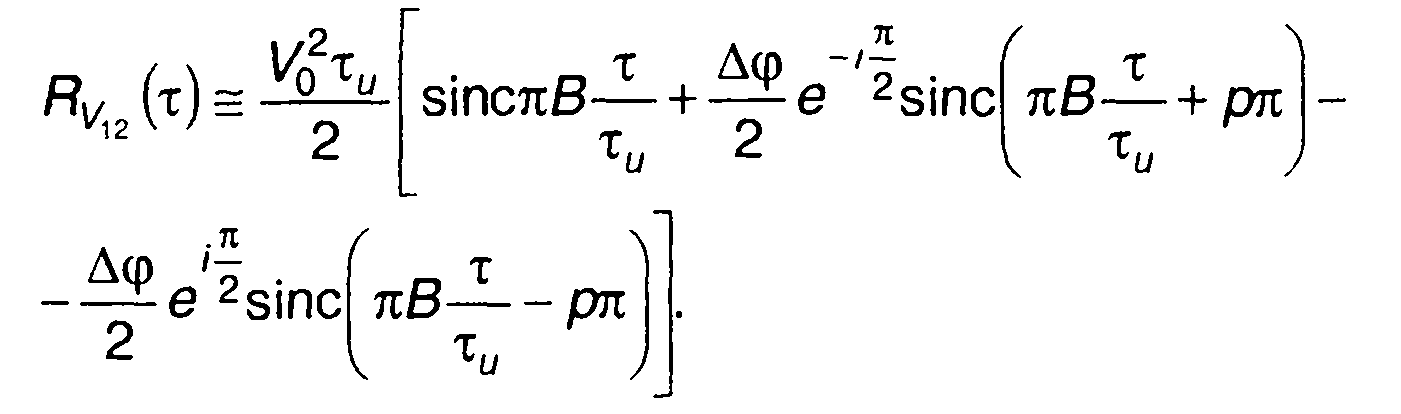(11.89)

где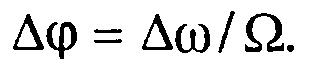

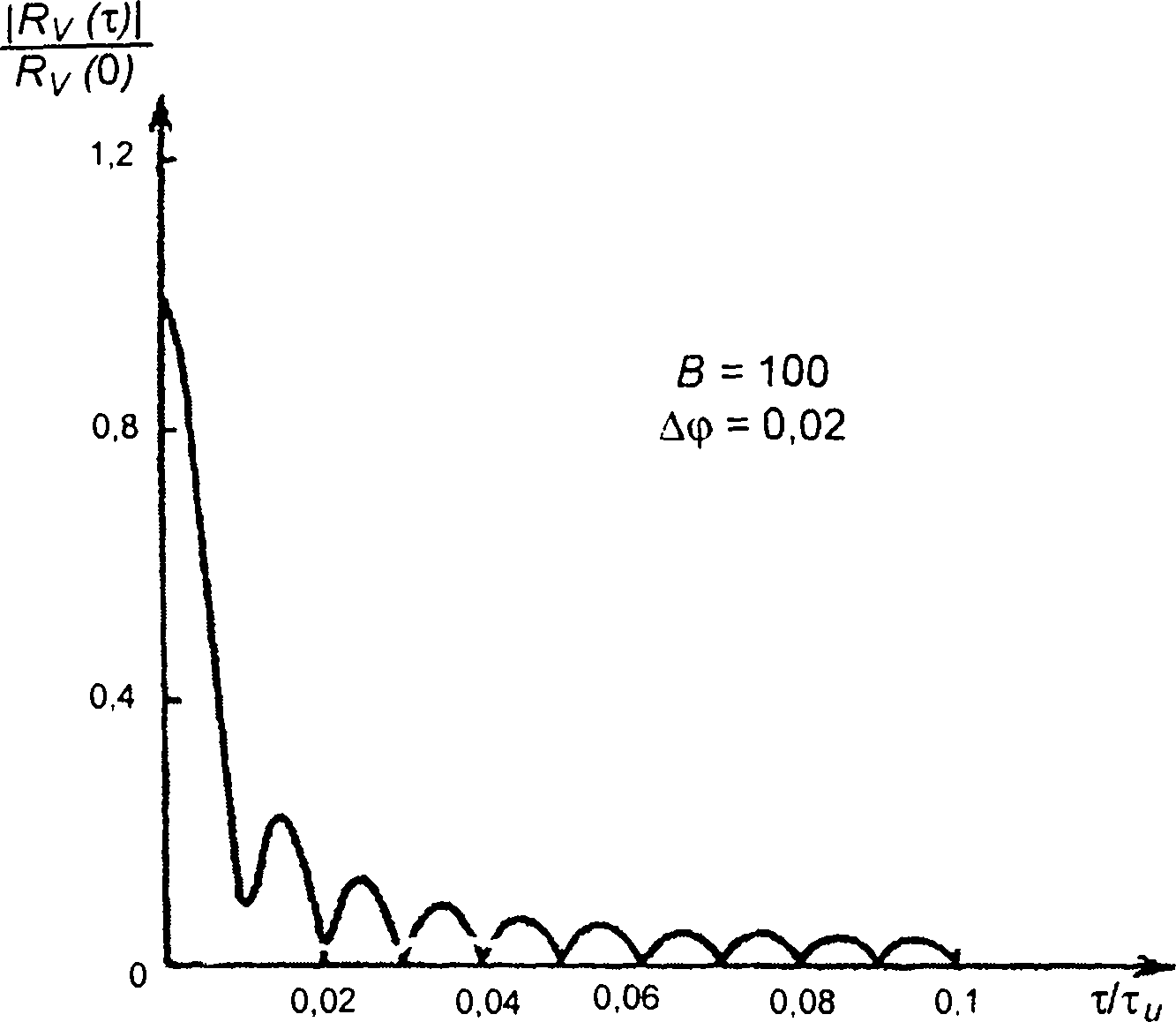
Рис. 11.13

График модуля взаимной корреляционной функции комплекс­ных огибающих сигналов при ∆φ = 0,2 (В=100) приведен на рис. 11.13.

11.8. Влияние ступенчатой аппроксимации закона изме­нения фазы на спектр сигнала

Преимущества цифровой техники заставляют обращаться к ней и при формировании ЧМ сигналов. Обычно модуляция производит­ся изменением фазы, закон изменения фазы получается ступенча­тым. Ступенчатый характер изменения фазы приводит к искажени­ям характеристик ЛЧМ сигнала.

При несимметричном законе ЧМ фаза описывается четной функцией (11.4)

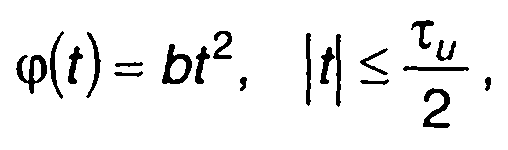(11.90)

где τ_и - длительность сигнала; b = (ω_д/τ_u; ω_д - девиация частоты.

При использовании цифровой техники фаза изменяется скачко­образно через заданный интервал времени Т, описывается кусоч­но-постоянной функцией

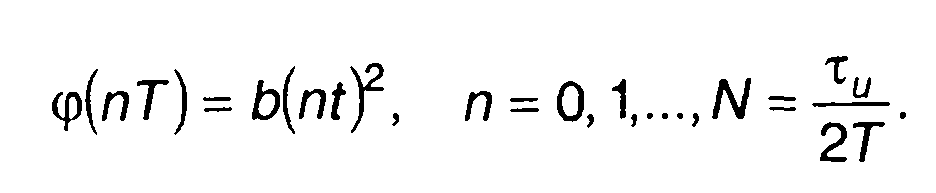(11.91)

С учетом шага квантования фазы

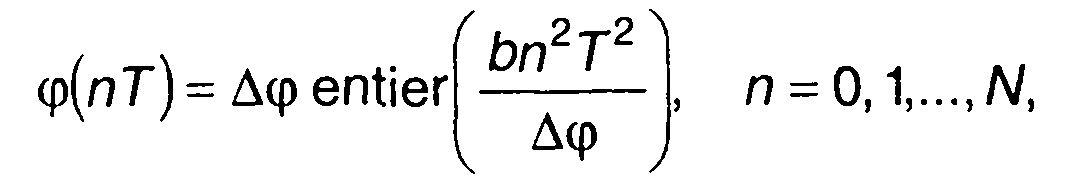(11.92)

где entier(x) - целая часть х.

Точность аппроксимации закона изменения фазы (11.90) зави­симостями (11.91) или (11.92) определяется выбором параметров Т и ∆φ. Выражение для спектра комплексной огибающей ЛЧМ сиг­нала при нечетносимметричном законе модуляции, исходя из (11.9), можем записать как

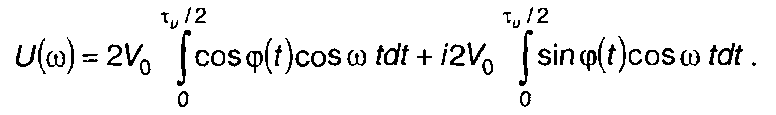(11.93)

Переходя в (11.93) от непрерывной функции φ(t) к кусочно­постоянной φ(nТ), интегралы в (11.93) представим в виде

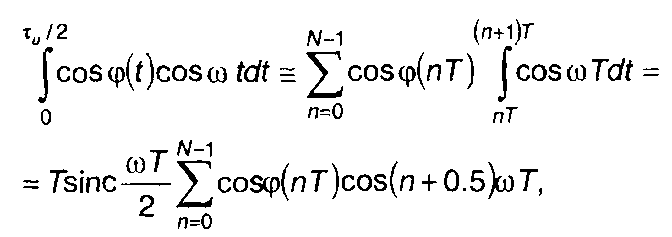(11.94)

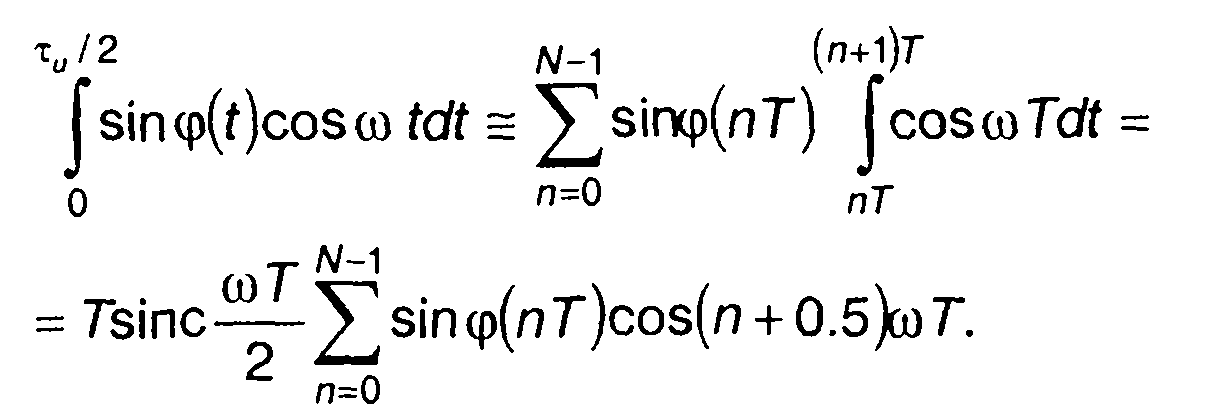(11.95)

Подстановка (11.94) и (11.95) в (11.93) дает

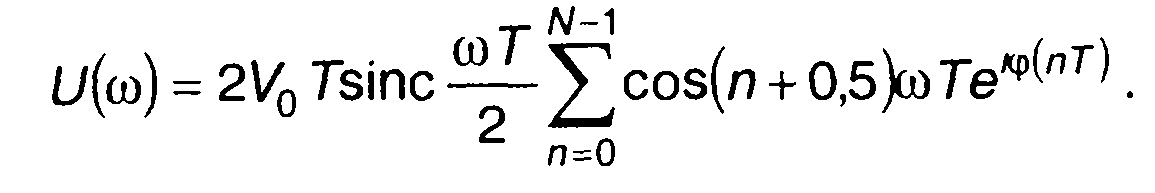(11.96)

Амплитудный спектр описывается выражением

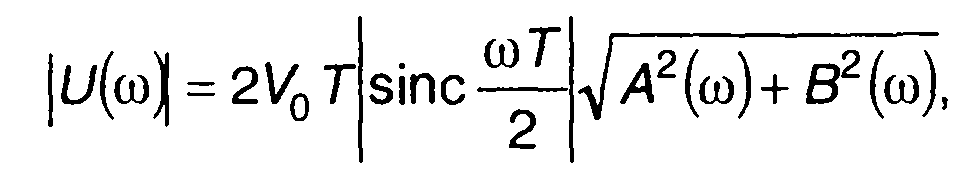(11.97)

где

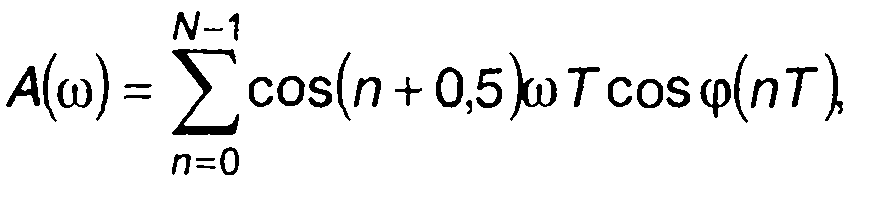(11.98)

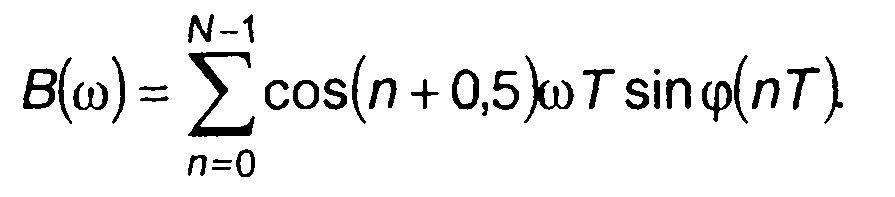(11.99)

Выражение (11.97) позволяет рассчитать амплитудный спектр ЛЧМ сигнала с учетом дискретизации по времени фазы (при циф­ровом методе формирования фазы). Результаты расчета ампли­тудного спектра с различными значениями интервала дискретиза­ции Г в виде графиков представлены на рис. 11.14. На рис. 11.14,а. приведен график спектра при значении интервала дискретизации Т₀, выбранного из условия Найквиста и практически не влияющего на спектр формируемого сигнала. На рис. 11.14,б приведен график спектра ЛЧМ сигнала, сформированного с интервалом дискретиза­ции 2,5Т₀. Влияние дискретизации во времени на спектр сигнала

при задании закона изменения фазы заметно уже при T = 1,25 T₀ и значительно - при T = 2,57T₀ .

11.9. Прохождение ЛЧМ сигнала через согласованный фильтр

Передача сигналов сопровождается шумами, которые искажают передаваемую информацию. Обнаружение сигнала на фоне шума, определение его параметров является одной из важных задач при передаче информации при помощи радиосигналов. Уменьшение влияния шумов достигается различными способами, в том числе выбором характеристик цепей, через которые проходит смесь сиг­нала и шума. Цепи, обеспечивающие обнаружение сигнала на

фоне шума наилучшим образом, называются оптимальными цепями или оптимальными фильтрами. Описываются оптимальные фильт­ры с помощью импульсной или частотной характеристик. Выбор в качестве критерия оптимальности максимального отношения сиг­нал/шум на выходе цепи определяет импульсную характеристику оптимального фильтра как (часть 2)

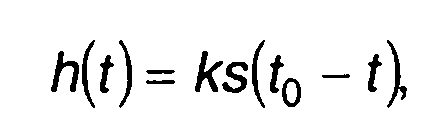(11.100)

где s(t) - сигнал на входе фильтра; k ,t₀ - нормирующий коэффи­циент и задержка.

Как правило, в (11.100) постоянная задержка опускается и выражение для h(t) записывается в виде

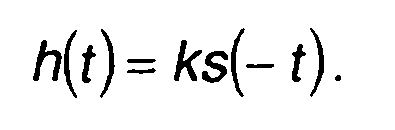(11.101)

Соответствующая частотная характеристика оптимального фильтра определяется как

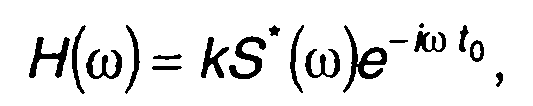(11.102)

где S(ω) - спектр сигнала на входе цепи.

Как и при записи выражения для h(t) постоянная задержка обычно опускается, нормирующий коэффициент k приравнивается единице

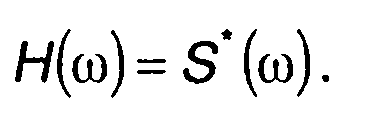(11.103)

Таким образом, характеристики оптимального фильтра опреде­ляются характеристиками обнаруживаемого сигнала. Поэтому та­кие фильтры называются согласованными. Фильтры, согласован­ные с ЧМ сигналами, выполняют и операцию сжатия импульсов. С учетом сказанного рассмотрение характеристик сигнала на вы­ходе согласованного с ЛЧМ сигналом фильтра представляет осо­бый практический интерес.

ЛЧМ сигнал при нечетной симметрии закона модуляции описы­вается выражением

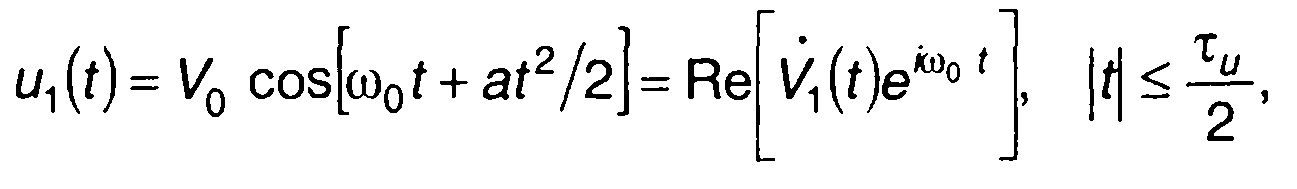(11.104)

где V₀ ,ω₀,τ_и - амплитуда, несущая частота и длительность сигнала;

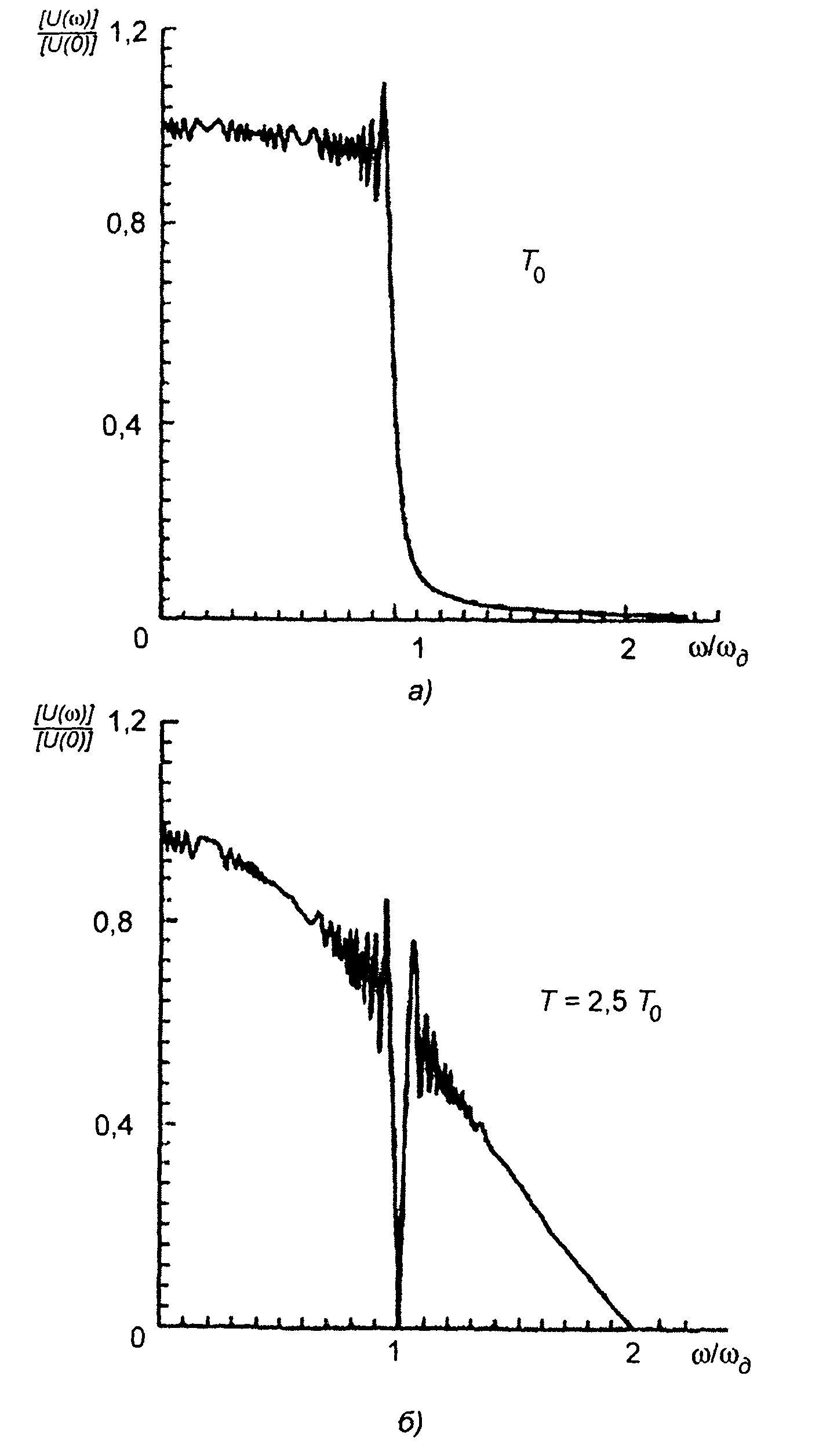
Рис. 11.14

а - скорость изменения частоты; 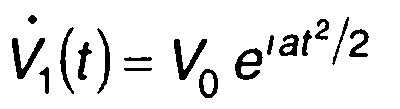- комплексная

огибающая сигнала.

Согласованный фильтр имеет импульсную характеристику, оп­ределяемую (11.101)

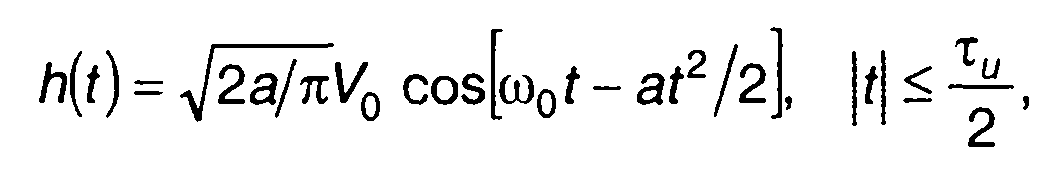(11.105)

где √(2a/π) - нормирующий коэффициент.

Сигнал на выходе согласованного фильтра определяется сверт­кой импульсной характеристики цепи и сигнала

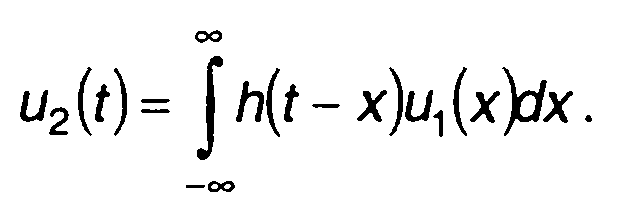(11.106)

В радиолокационных системах, в которых производится сжатие импульсов, особый интерес представляет влияние эффекта Доп­плера, вызываемого движением обнаруженного объекта, на вы­ходной сигнал. Выражение для сигнала с учетом частоты Допплера записывается в виде

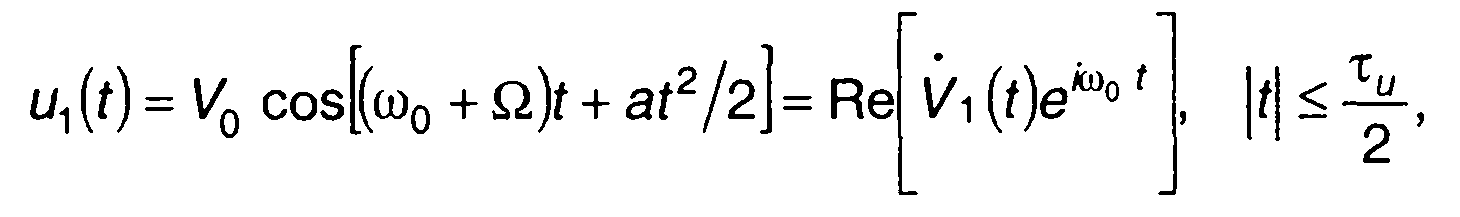(11.107)

где 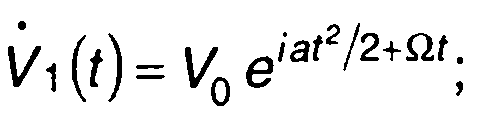Ω - частота Допплера.

Подставляя (11.105) и (11.107) в (11.106), для t > 0 запишем

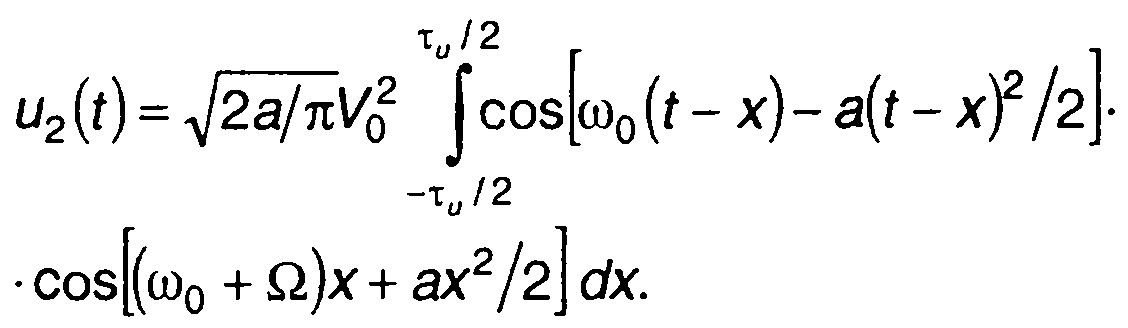(11.108)

Преобразуя (11.108) и опуская члены с удвоенной частотой, найдем

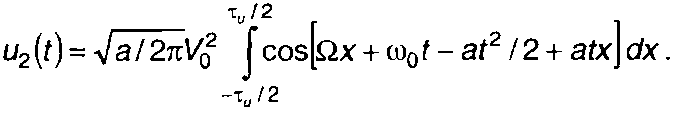(11.109)

Решая интеграл в (11.109) и преобразуя полученное решение, запишем

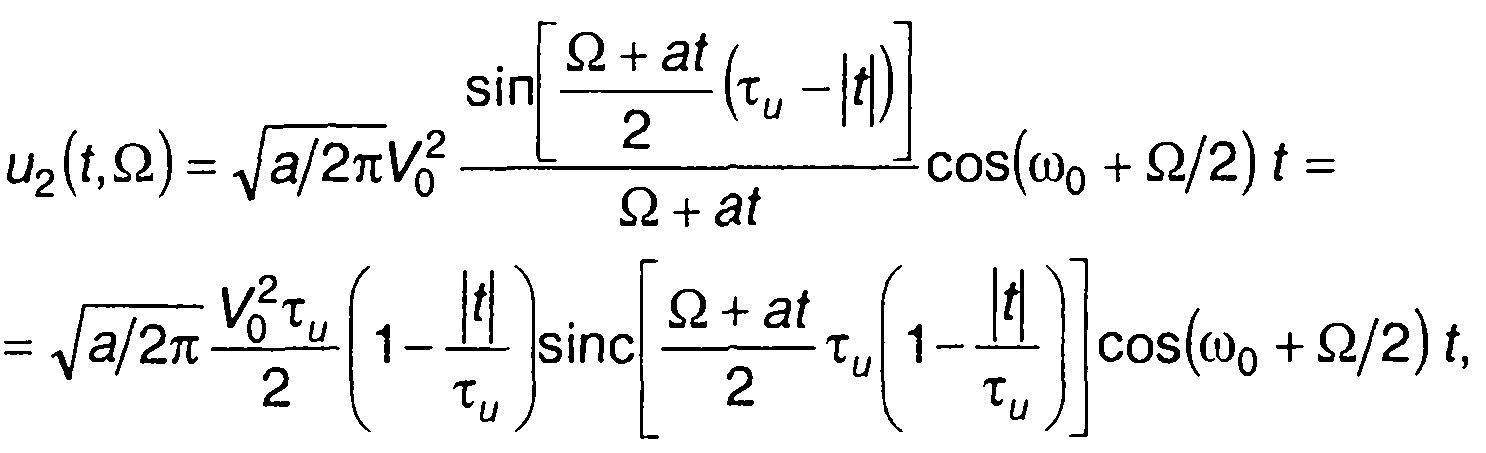(11.110)

где sincx = sinx/x.

При Ω = 0

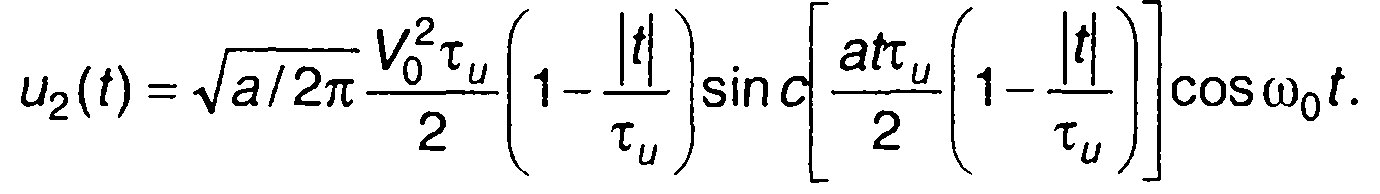(11.111)

Огибающая u₂(t) с точностью до постоянного коэффициента совпадает с (11.45). Таким образом, корреляционная функция ЛЧМ сигнала позволяет описывать огибающую сигнала на выходе со­гласованного фильтра (при подаче на вход ЛЧМ сигнала).

Анализ выражения, определяющего u₂(t,Ω), и расчетного вы­ражения, полученного для ЛЧМ сигнала, показывает, что они сов­падают с выражениями для обобщенной корреляционной функции (разд. 8).

Учитывая следующее равенство

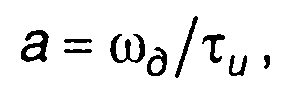
где ω_д - девиация частоты,

(11.110) можем переписать в виде

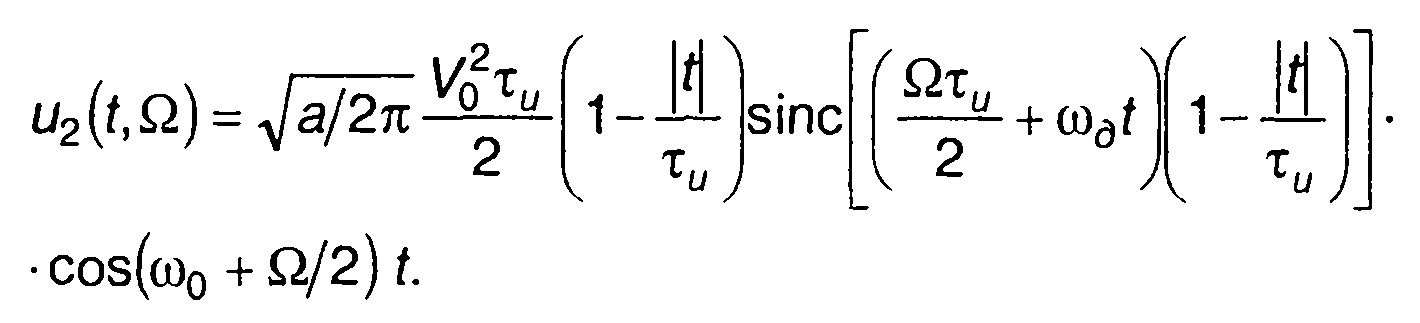(11.112)

При больших значениях ω_д (при больших значениях базы сиг­нала В = ω_дτ_и/π) можно принять

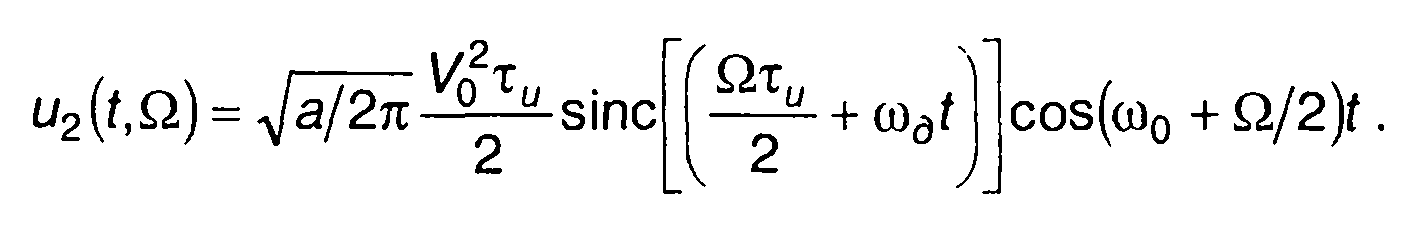(11.113)

Максимум функции u₂(t,Q) достигается при значении t, полу­чаемом из следующего уравнения:

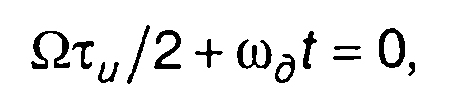
т.е. при t = -Ωτ_u/2ω_д, где ω_д - девиация частоты.

11.10 Импульсные сигналы с нелинейной частотной мо­дуляцией

Для сигналов с внутриимпульсной ЧМ нелинейный закон модуля­ции - наиболее общий случай. Рассмотрение НЧМ сигналов расши­ряет рамки анализа импульсных ЧМ сигналов, позволяет исследовать влияние закона модуляции на характеристики сигнала.

11.10.1. НЧМ сигналы со степенным законом модуляции

Импульсный ЧМ сигнал описывается выражением

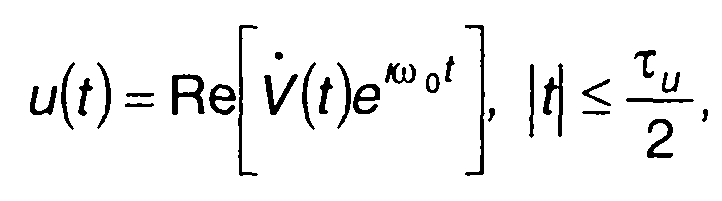(11.114)

где V/(t) - комплексная огибающая сигнала;

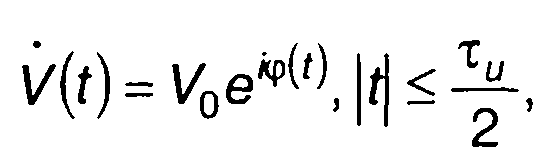
V₀,ω₀,φ(t) - амплитуда, несущая частота и фаза сигнала; τ_и- дли­тельность импульса.

Частота сигнала определяется как

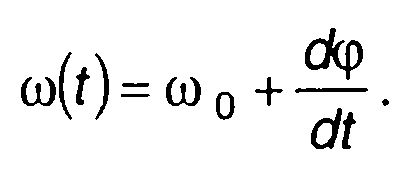(11.115)

Достаточно общей нелинейной зависимостью для переменной составляющей частоты, можно считать, является степенная зави­симость. Поэтому при рассмотрении НЧМ целесообразно рассмот­реть ее в первую очередь.

При нечетной симметрии закона модуляции (наиболее распро­страненный на практике случай) выражение для частоты запишем в виде (рис. 11.15)

(11.116)

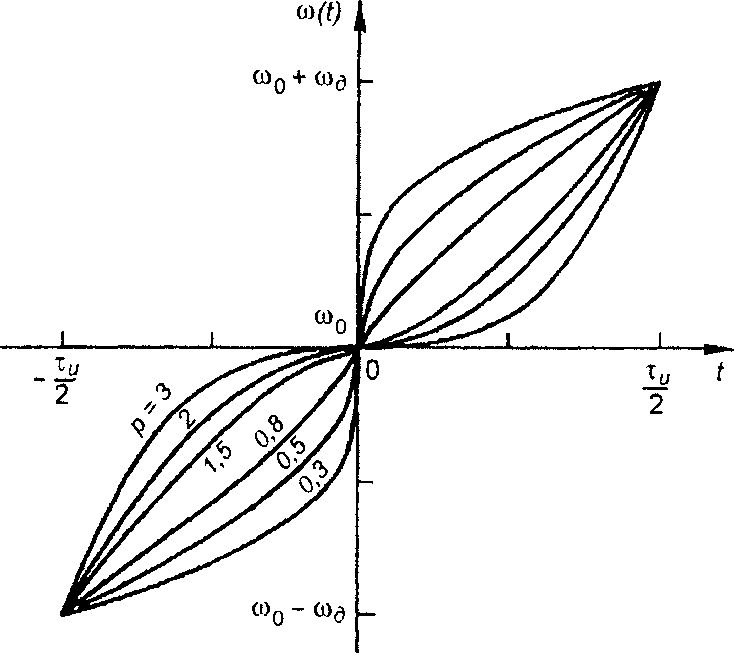
Рис. 11.15

где 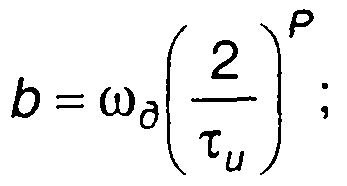ω_д - девиация частоты; р - показатель степени,

определяющий характер изменения частоты;

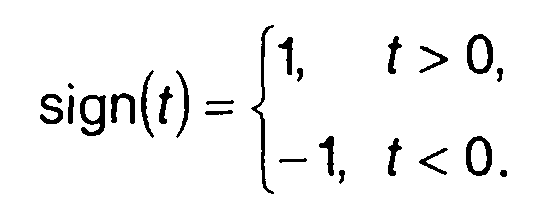
Фаза сигнала в этом случае

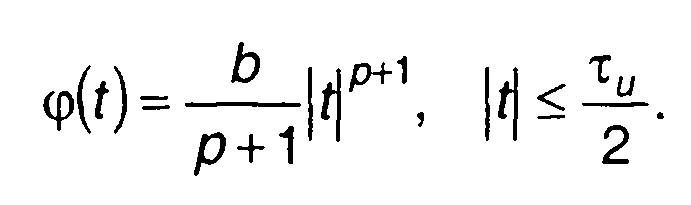(11.117)

Спектральная плотность комплексной огибающей сигнала опре­деляется выражением

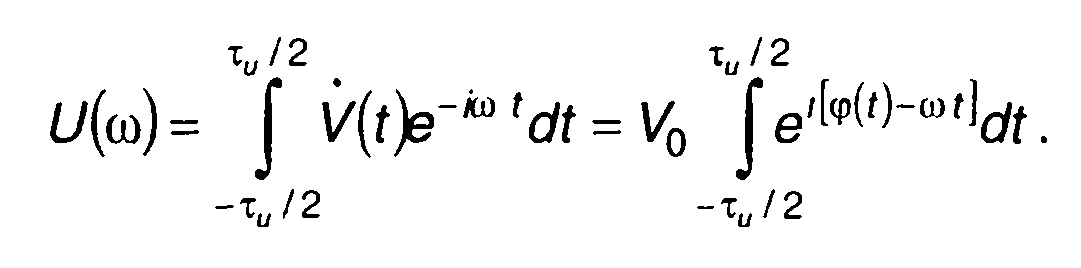(11.118)

Интегрирование в (11.118.) с использованием известных решений возможно только при р = 1 (линейный закон модуляции). В общем случае решение может быть получено только численным методом.

Спектральную плотность комплексной огибающей сигнала пред­ставим в виде

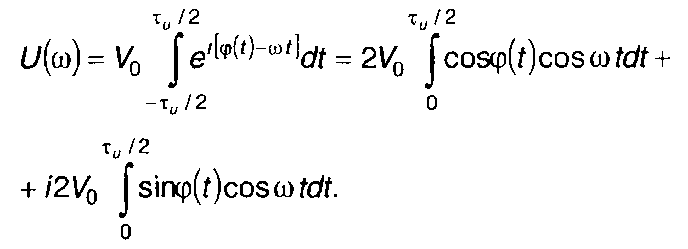(11.119)

Разобьем интервал [0, τ_u/2] на N участков длительностью ∆t = τ_u/2N. Аппроксимируем φ(t) кусочно-постоянной функцией, значения которой совпадают с φ(t) в точках разбиения. При такой аппроксимации фаза на n-м участке разбиения описывается выра­жением

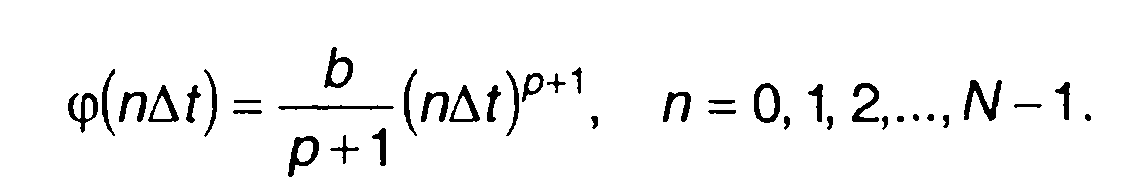(11.120)

Подставляя (11.120) в подинтегральные выражения (11.119), получим

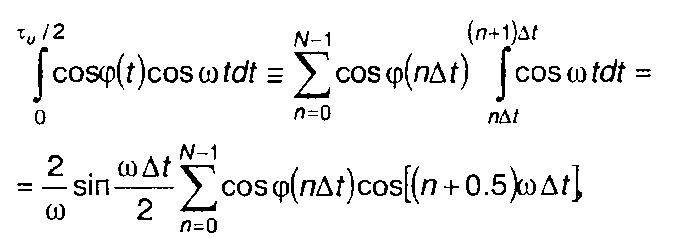(11.121)

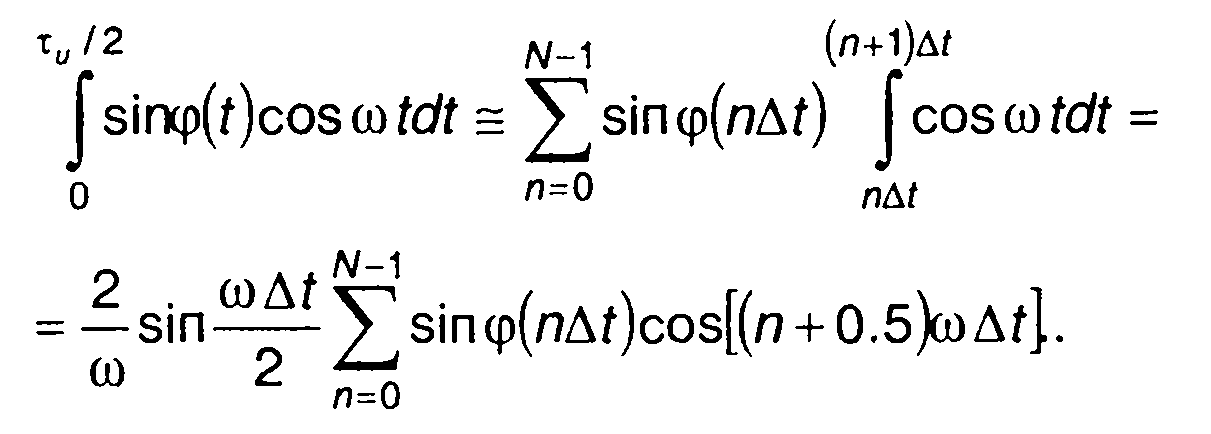(11.122)

С учетом (11.121) и (11.122) расчетное выражение для U(ω) представим в виде

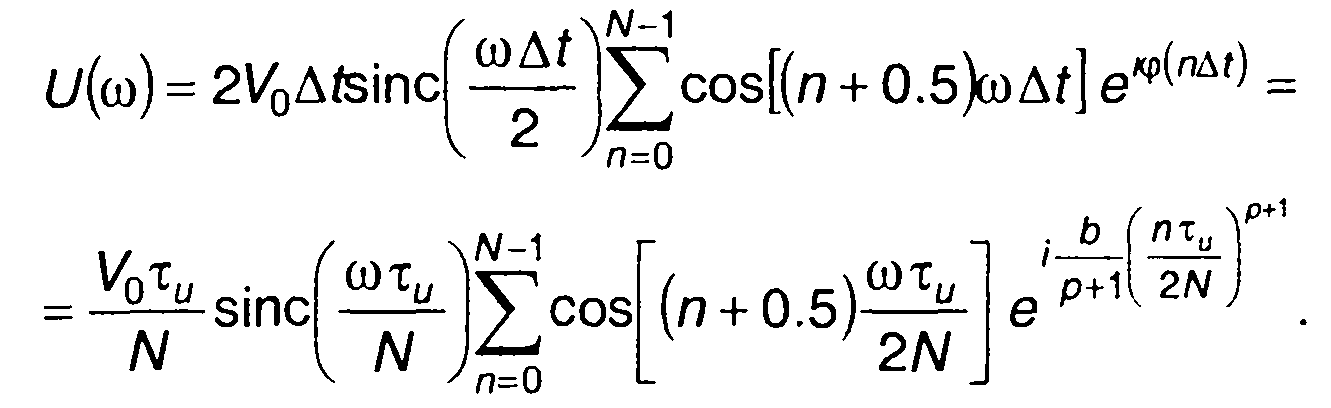(11.123)

Графики амплитудного спектра комплексной огибающей сигнала при различных значениях p, полученные в результате расчета (11.123), приведены на рис. 11.16. Анализ графиков показывает, что при p =1 (ЛЧМ) спектр является достаточно равномерным в полосе частот |со|(со_а. При уменьшении p (p< 1) максимум спектра появляется на |ω| ≡ ω_д. При увеличении p(p>1) максимум спектра появляется на частотах близких к ω = 0 . Чем больше p отличается от единицы, тем более выражен максимум.

Корреляционная функция комплексной огибающей сигнала мо­жет быть определена с использованием выражения (11.49) с под­становкой в него

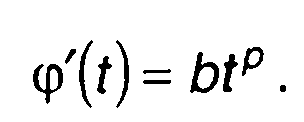(11.124)

После подстановки выражение для R_у(т) примет вид

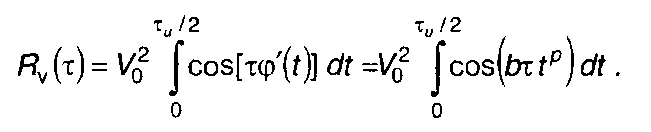(11.125)

Решение (11.125) в конечном виде возможно только при p =1 - выражение (11.50) и p = 2. Для p = 2 из (11.125) получим

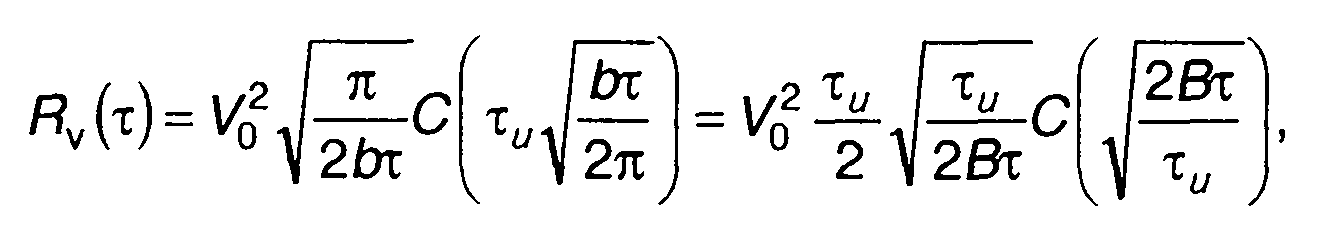(11.126)

где С(х) - интеграл Френеля; В - база сигнала.

В общем случае (при произвольном значении р) решение инте­грала (11.125) возможно только численно. Используя кусочно­постоянную аппроксимацию

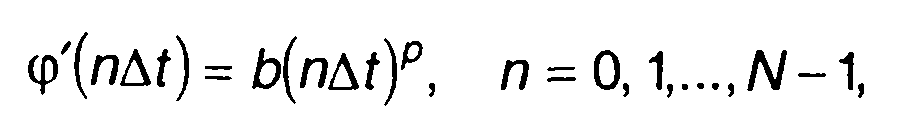(11.127)

интеграл в (11.115) представим в виде

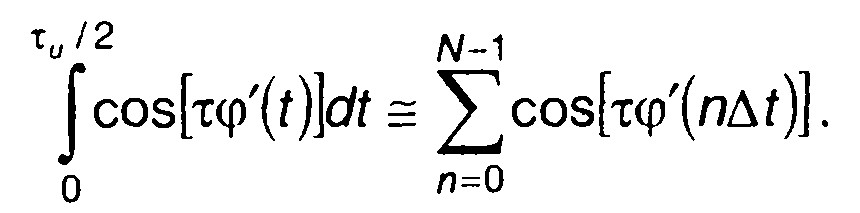(11.128)

С учетом (12.15) выражение (12.12) представим в виде

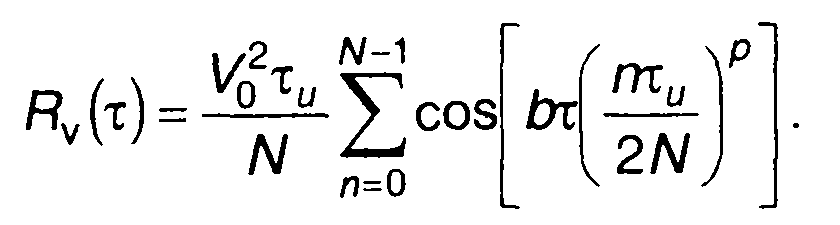(11.129)

Графики модуля корреляционной функции |R_V(т)|, полученные при расчете (11.129) при различных значениях p, приведены на рис. 11.17. Для сравнения дан и график |R_v(τ)| для ЛЧМ - сигнала

(p = 1). Анализ графиков показывает, что при p < 1 огибающая имеет лепестковую структуру. По мере уменьшения p главный максимум сужается, а уровень боковых лепестков растет. При p >1 лепестковая структура огибающей пропадает, колебания огибающей сглаживаются, появляется «пьедестал». Сравнение корреляционной функции комплексной огибающей сигнала со степенным законом модуляции и ЛЧМ сигнала показывает, что при p > 1 уровень боковых лепестков уменьшается. Корреляцион­ная функция становится более удобной при использовании ее в системах, где необходимо повысить разрешающую способность при сжатии сигнала.

11.10.2. НЧМ сигналы с законом модуляции, описываемым тригонометрическими функциями

Рассмотрим зависимость ω(t), описываемую выражением (рис. 11.18)

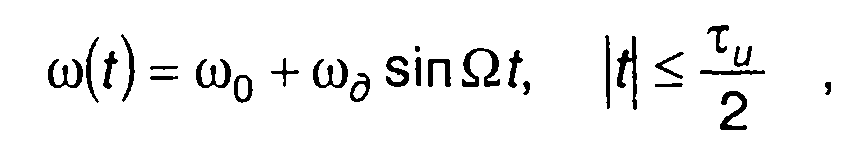(11.130)

где ω₀,ω_д - несущая частота и девиация; τ_и - длительность им­пульса; Q = п/т_и .

Фаза сигнала

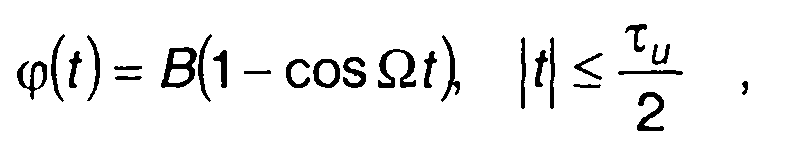(11.131)

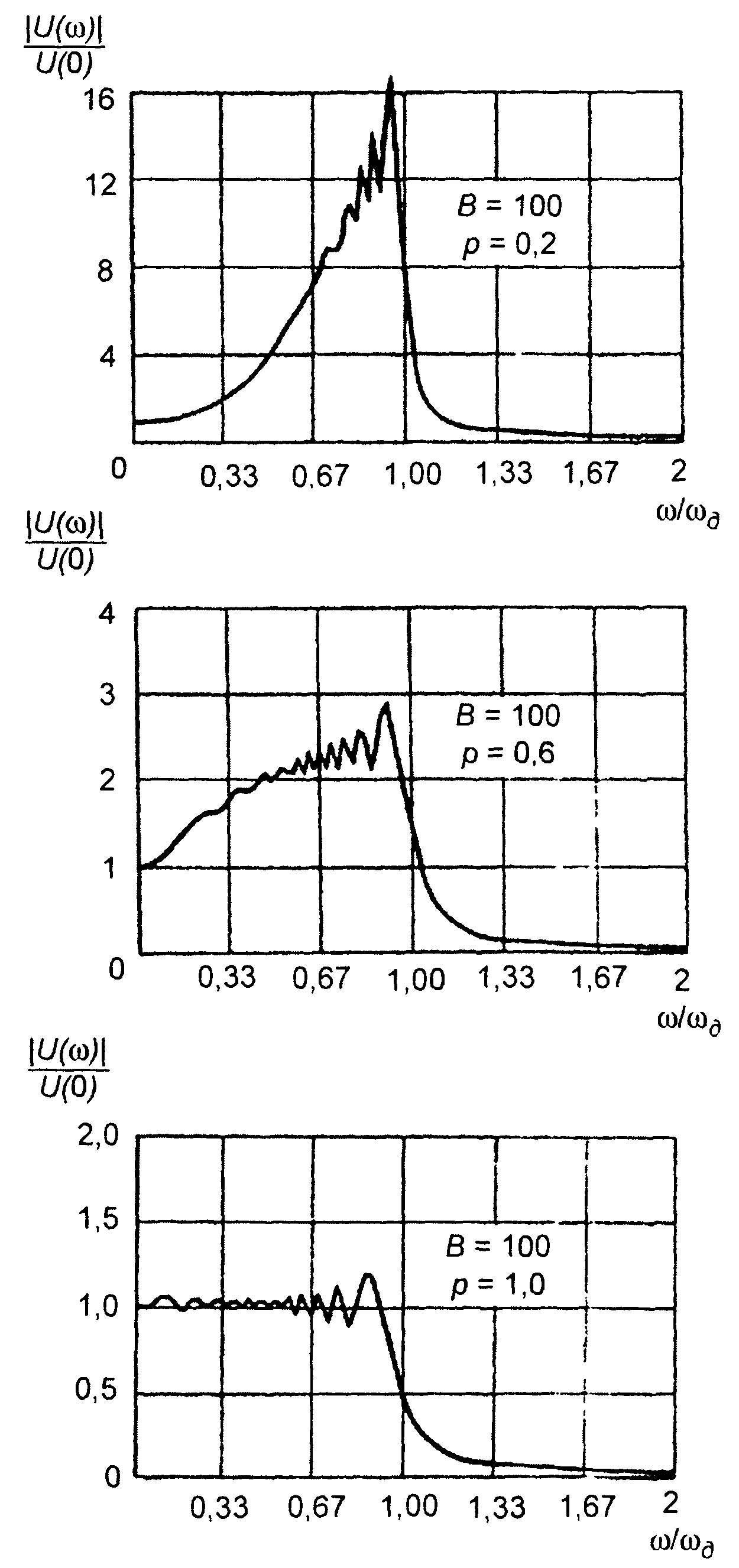
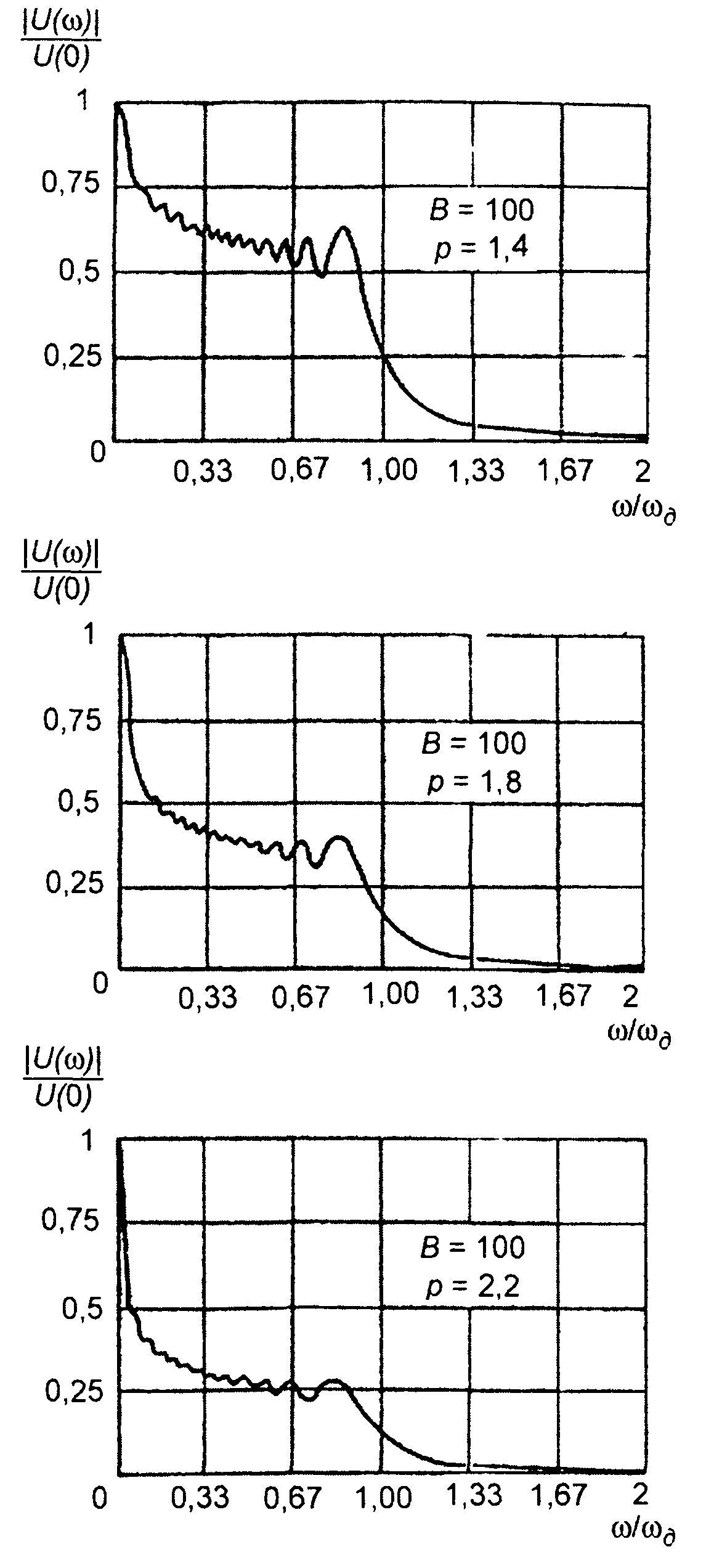
Рис. 11.16

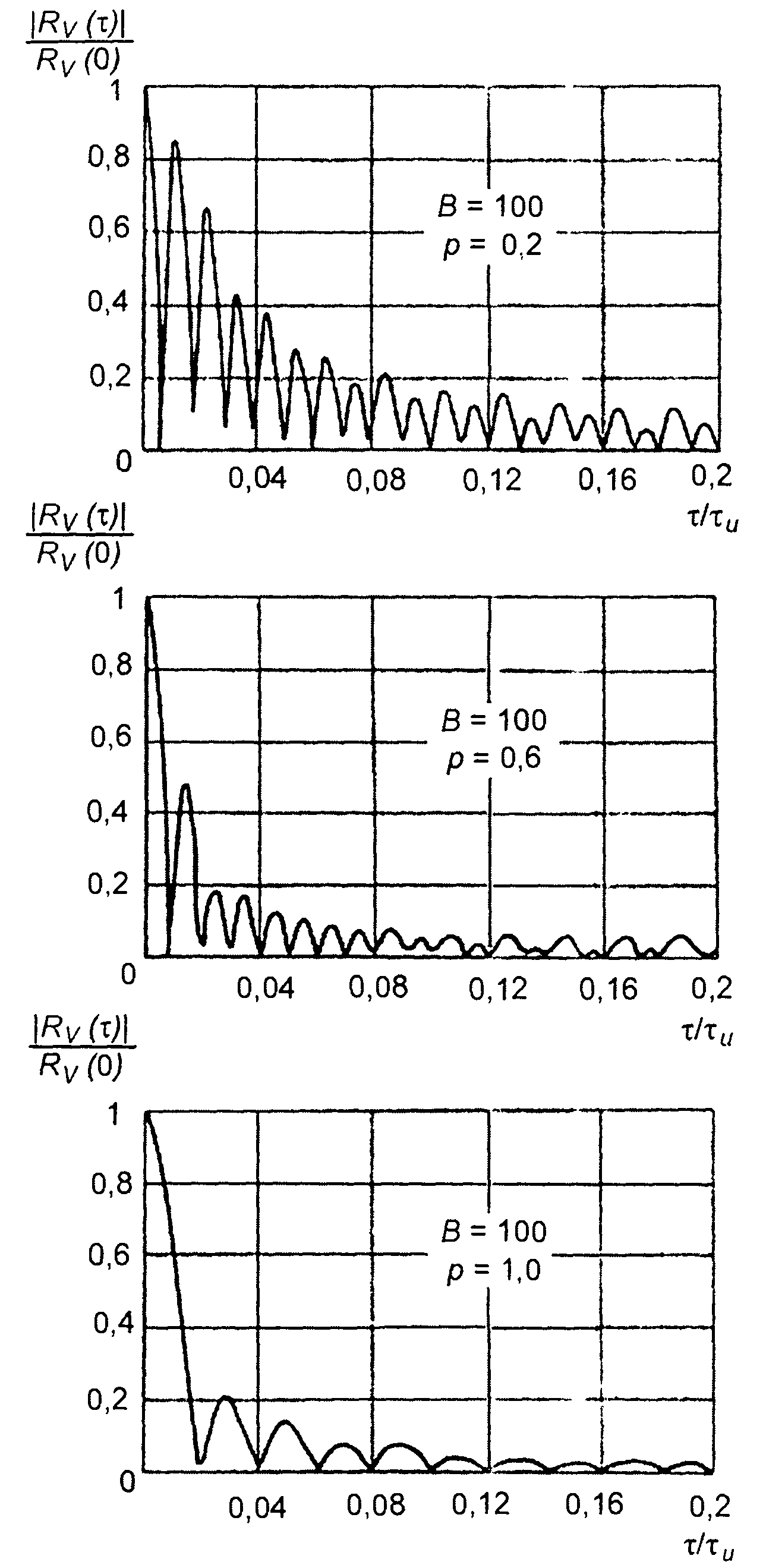
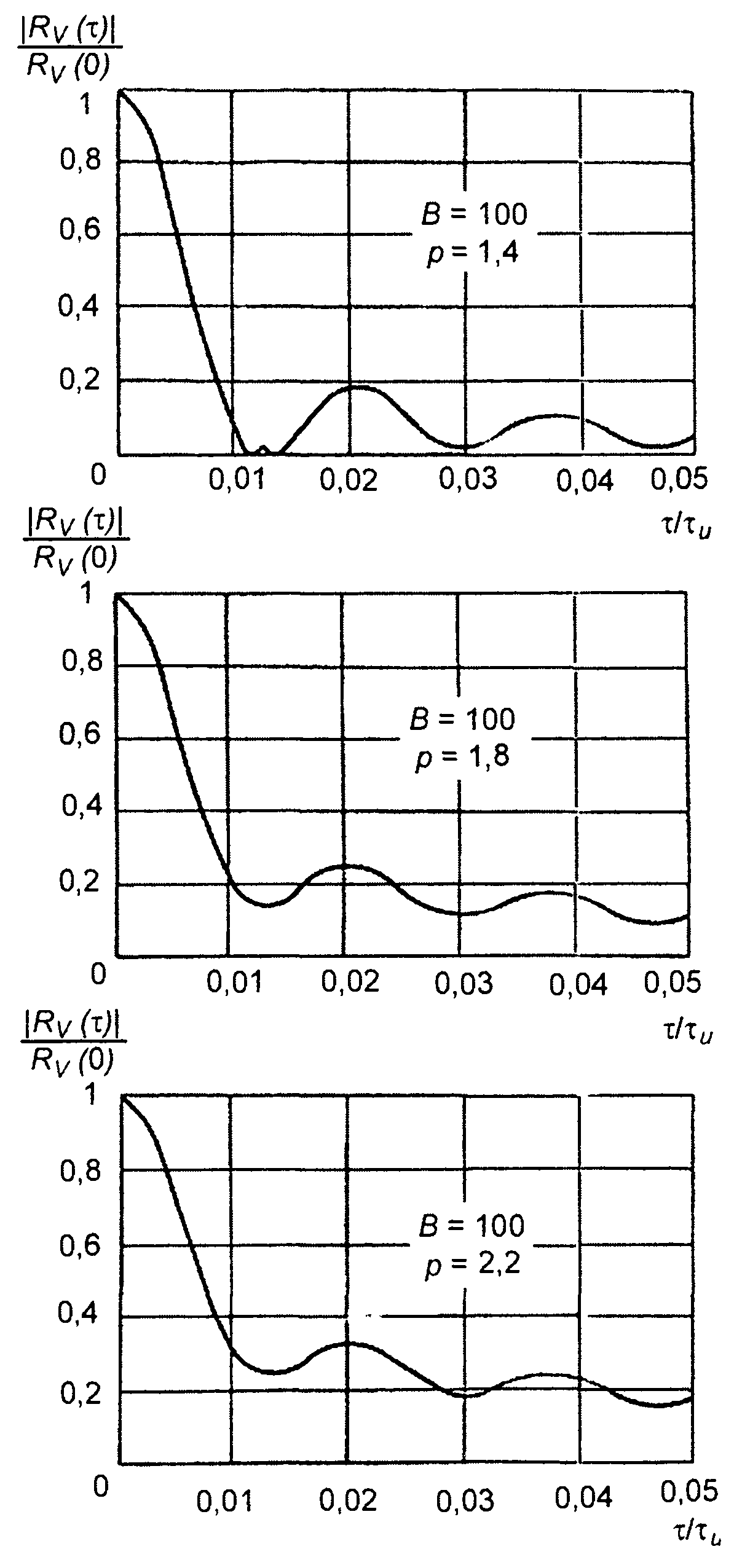
Рис. 11.17

где 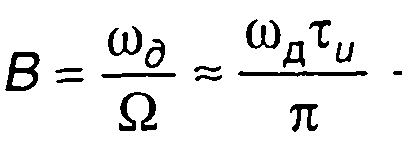- база сигнала.

Спектральная плотность комплексной огибающей сигнала опре­делим, подставив (11.131) в (11.118),

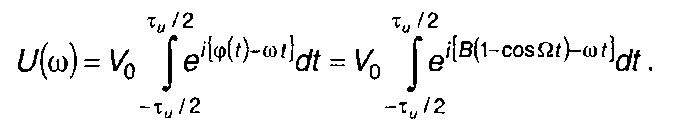(11.132)

Используя (11.69), из (11.132) получаем

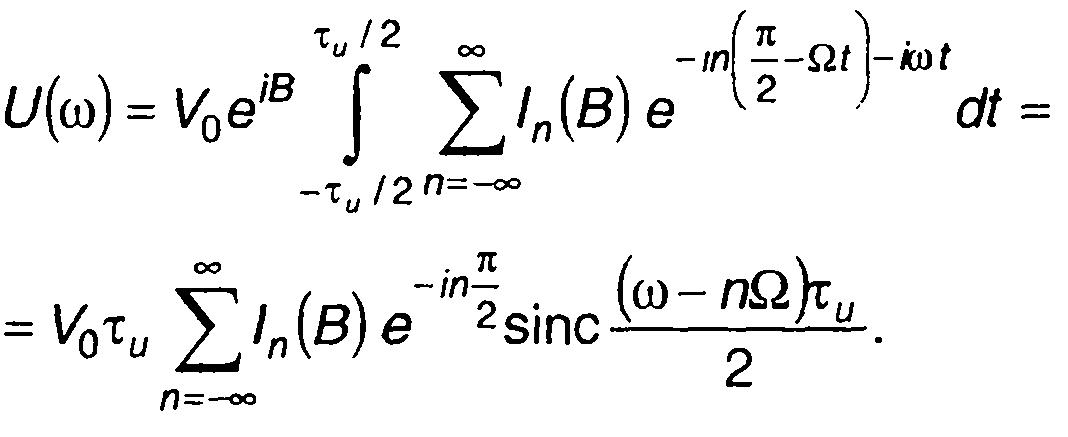(11.133)

Полученное выражение представляет разложение спектральной плотности комплексной огибающей сигнала в ряд по базисным функциям

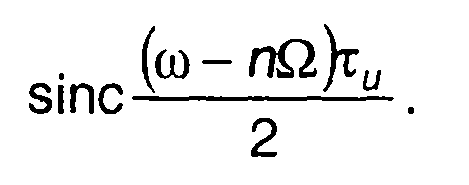
Коэффициенты слагаемых определяются произведением функций Бесселя l_n(В) и множителя е ^–in(π/2) . Число членов ряда

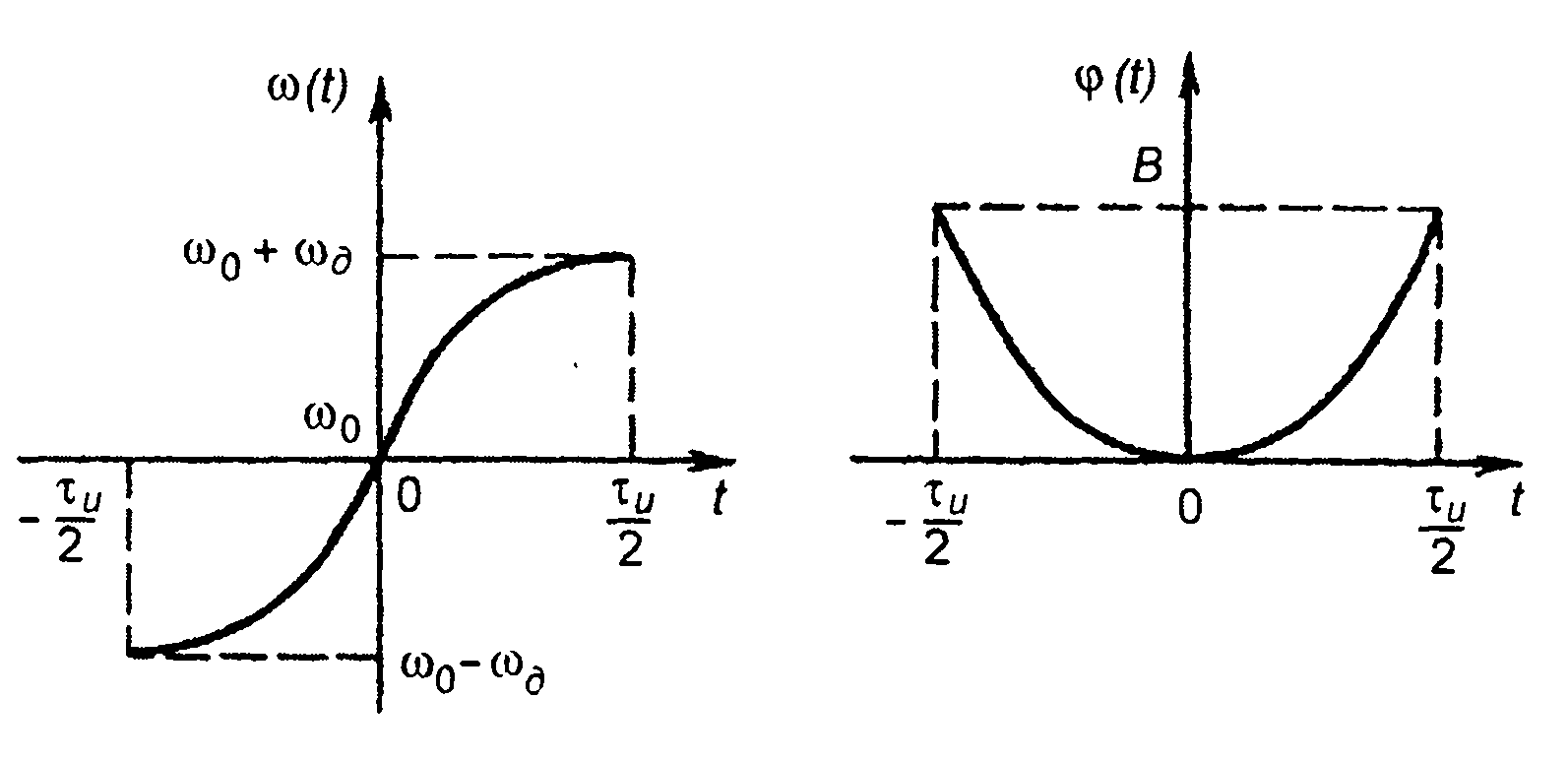
Рис. 11.18

бесконечно. Однако при расчете, учитывая свойства Бесселевых функций, можно ограничиться числом слагаемых N, зависящим от В (разд. 10).

Корреляционная функция комплексной огибающей сигнала оп­ределяется (11.43)

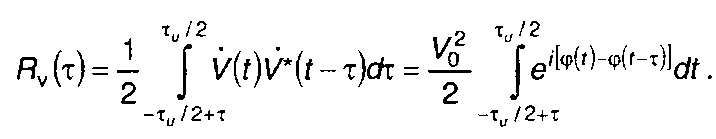(11.134)

Подставляя в (11.134) выражение для φ(t), (11.131), запишем

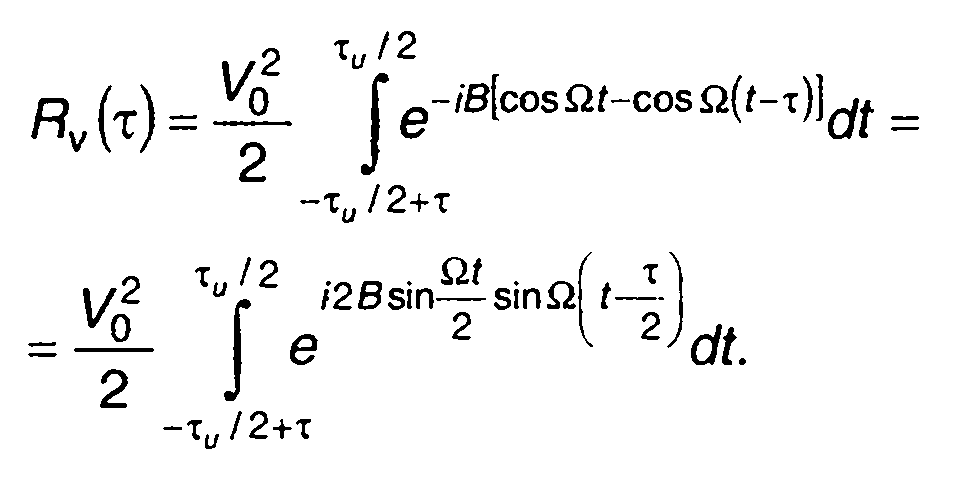(11.135)

Воспользовавшись разложением (11.69), выражение для R_v(τ) представим в виде

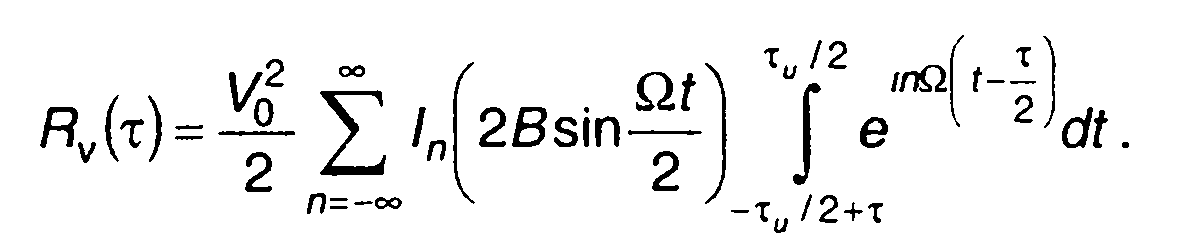(11.136)

Решая (11.136), получаем для т > 0

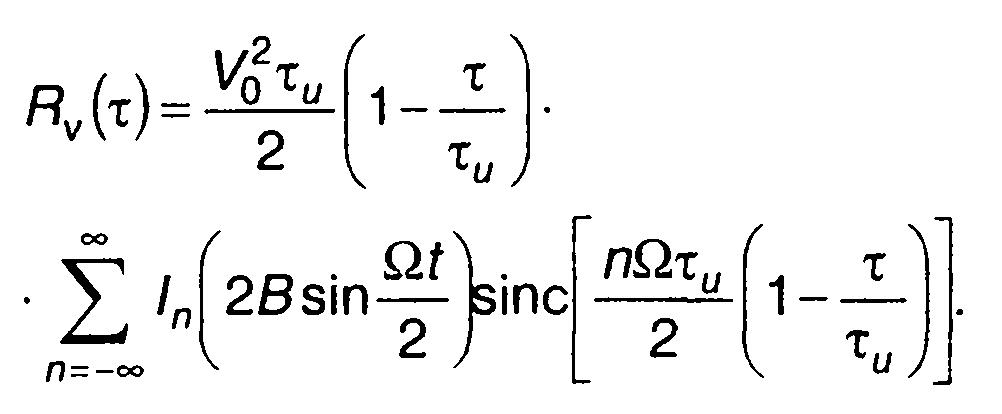(11.137)

При τ<<τ_и ( при больших значениях В , это условие практиче­ски не накладывает ограничений, о чем указывалось ранее ) можно принять

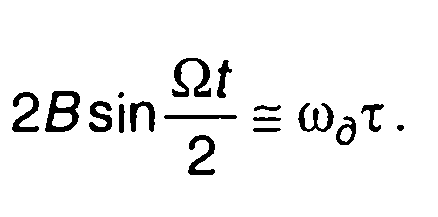
Выражение для R_v(т) запишется в виде

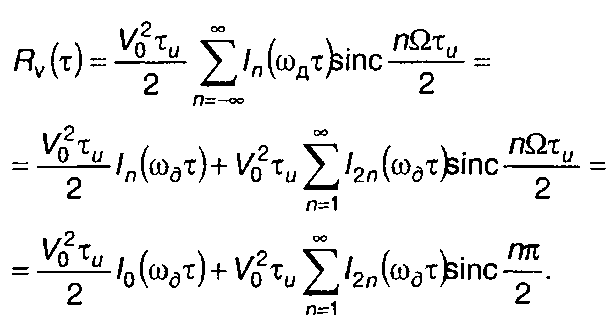(11.138)

Имея спектральную плотность импульсного ЧМ сигнала, можно получить спектр соответствующего периодического сигнала (сигна­ла, получающегося периодическим повторением импульсного сигна­ла с периодом Т = τ_u). Проиллюстрируем это положение на приме­ре тонально модулированного ЧМ сигнала (разд. 10). Для этого рас­смотрим импульсный ЧМ сигнал с законом модуляции, описывае­мым зависимостью

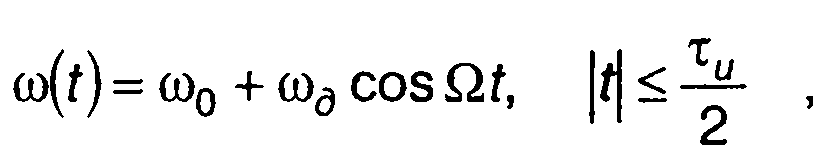(11.139)

где ω₀,ω_д - несущая частота и девиация; τ_и - длительность им­пульса; Ω = π/τ_и .

Фаза сигнала

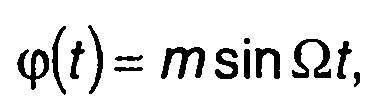(11.140)

где

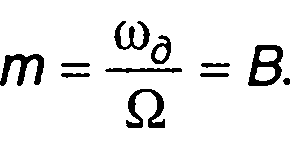(11.141)

Спектральная плотность комплексной огибающей такого сигна­ла равна

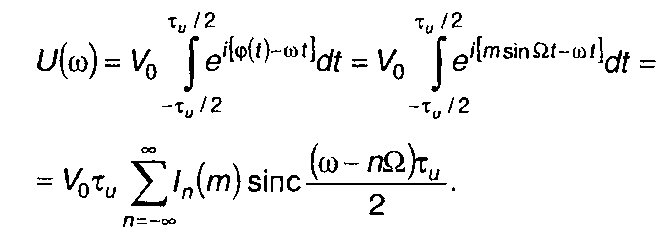(11.142)

Полученное выражение представляет разложение функции U(ω) в ряд по базисным функциям

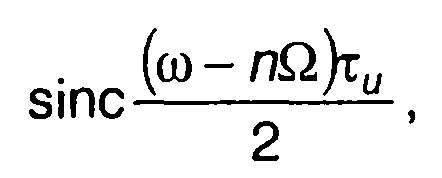
с коэффициентами, определяемыми функциями Бесселя l_n(т).

Перейдем к непрерывному, периодическому сигналу с тональ­ной модуляцией, который получается периодическим повторением рассмотренного импульсного сигнала. Период сигнала Т = τ_и. Спектр такого сигнала определяется из соотношения

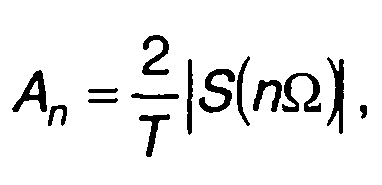(11.143)

где S(ω) - спектральная плотность исходного импульсного сиг­нала.

Как следует из (11.142), функции Бесселя l_n(т) определяют

значения спектральной плотности S(ω) и спектра непрерывного сигнала А_n на частотах ω₀ ± nΩ. С учетом этого получим

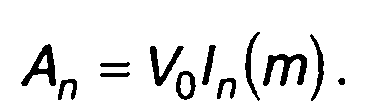(11.144)

Следовательно, для непрерывного ЧМ сигнала можем записать

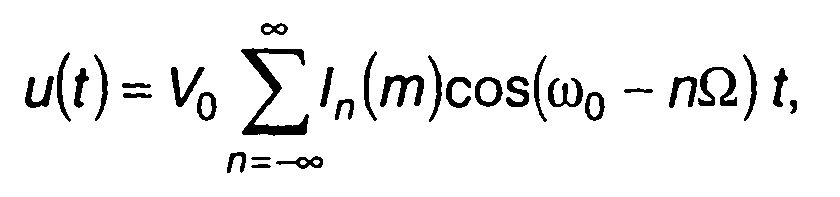(11.145)

что совпадает с ранее полученным выражением (разд. 10). Таким образом, используя спектральную плотность импульсного ЧМ сиг­нала, перешли к известному разложению тонально модулирован­ного сигнала.

11.10.3. НЧМ сигналы с законом модуляции, описываемым суммой линейной и тригонометрической функций

Рассмотрим зависимость ω(t), описываемую выражением (рис. 11.19)

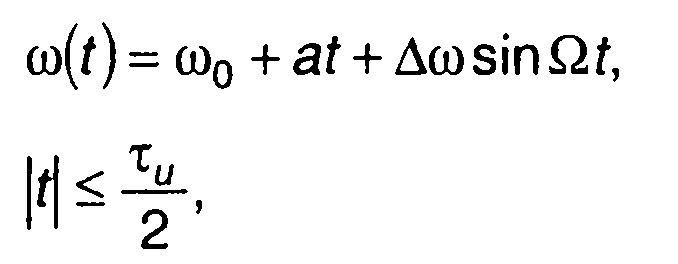(11.146)

где а = 2ω_д/τ_и, ω_д- девиация частоты; ∆ω - параметр зависи­мости; Ω=2π/t_u.

Зависимость (11.146) может рассматриваться как один из видов нелинейных зависимостей π(t), встречающихся на практике, может

описывать и линейный закон ЧМ с искажениями. Фаза сигнала, со­ответствующая (11.146), определяется выражением

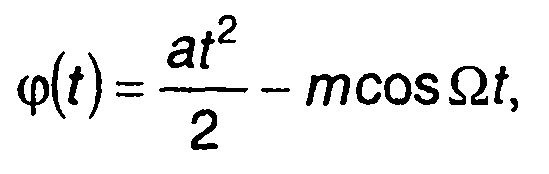(11.147)

где

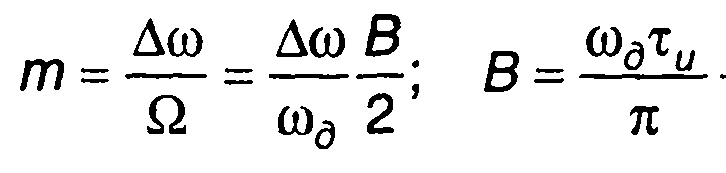- база сигнала.

Спектральная плотность комплексной огибающей сигнала

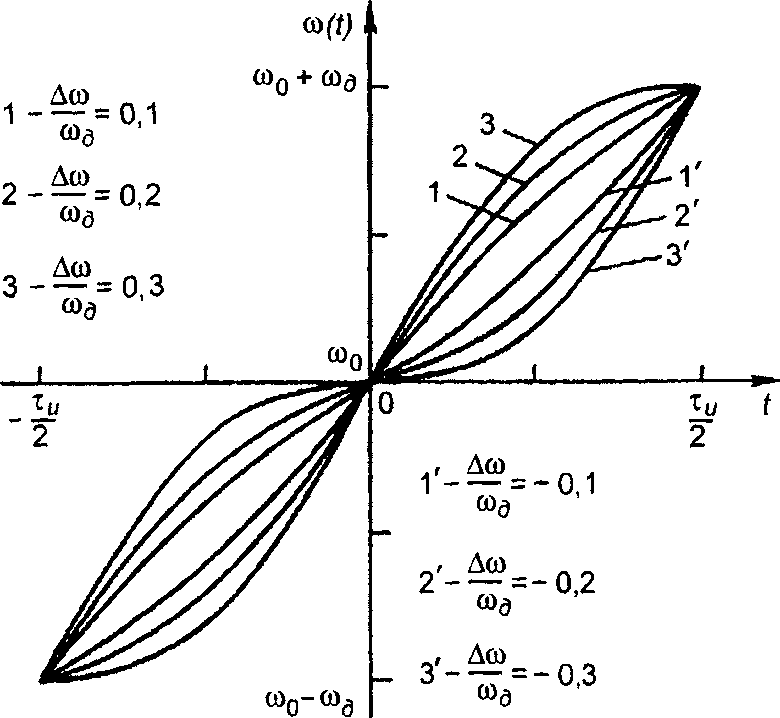
Рис. 11.19

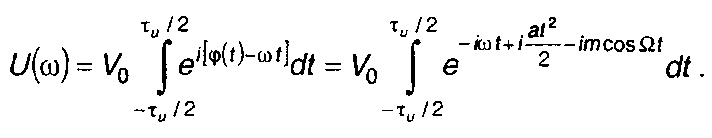
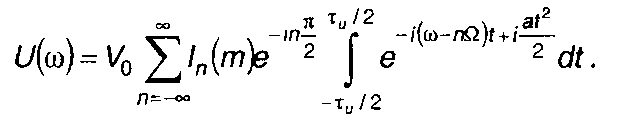
Решая интеграл, получим

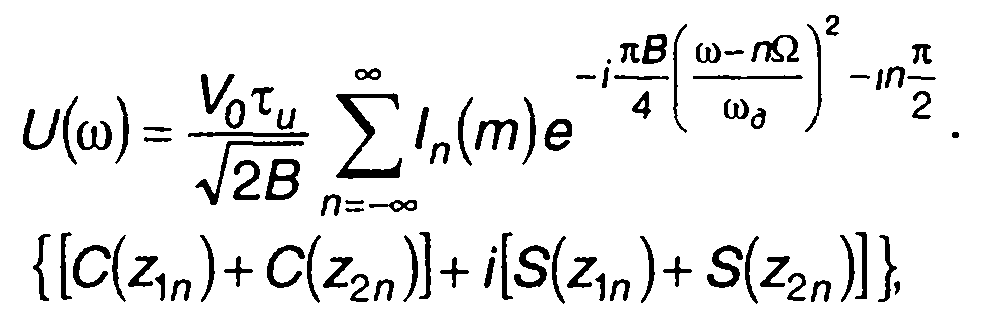
где

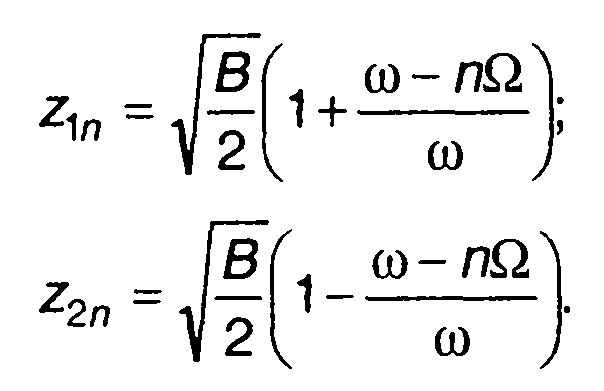
Графики амплитудного спектра |U(ω)|, полученные в результате расчета по (11.150) при различных значениях ∆ω, приведены на рис. 11.20 (∆ω < 0) и на рис. 11.21 (∆ω > 0). Как следует из анализа графиков, спектр комплексной огибающей сигнала сосредоточен в полосе частот |ω| ≤ ω_д. Вид спектра определяется зависимостью ω(t). На частотах, для которых скорость изменения ω(t) увеличи­вается, величина |U(ω)| уменьшается.

Корреляционная функция комплексной огибающей сигнала оп­ределяется выражением (т > 0)

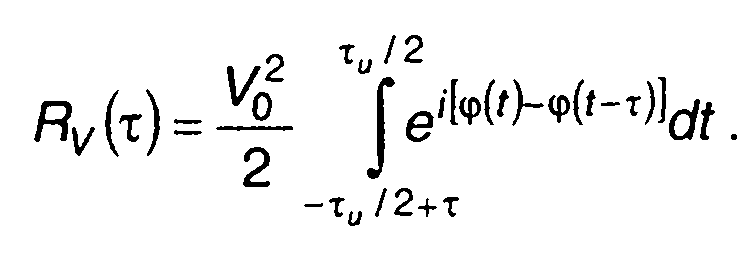
С учетом (11.151) выражение для R(τ) запишем в виде

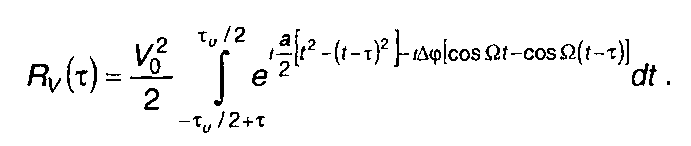(11.152)

Преобразовав (11.152), получим

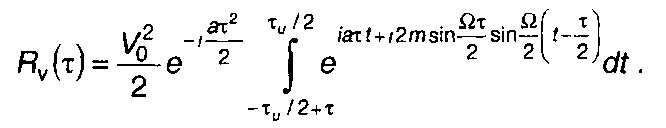(11.153)

С учетом разложения (11.69) запишем

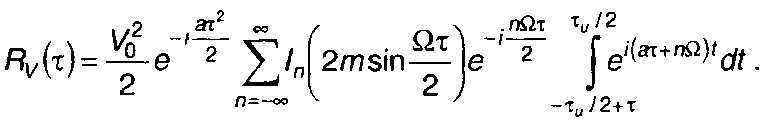(11.154)

Решая интеграл в (11.154), находим

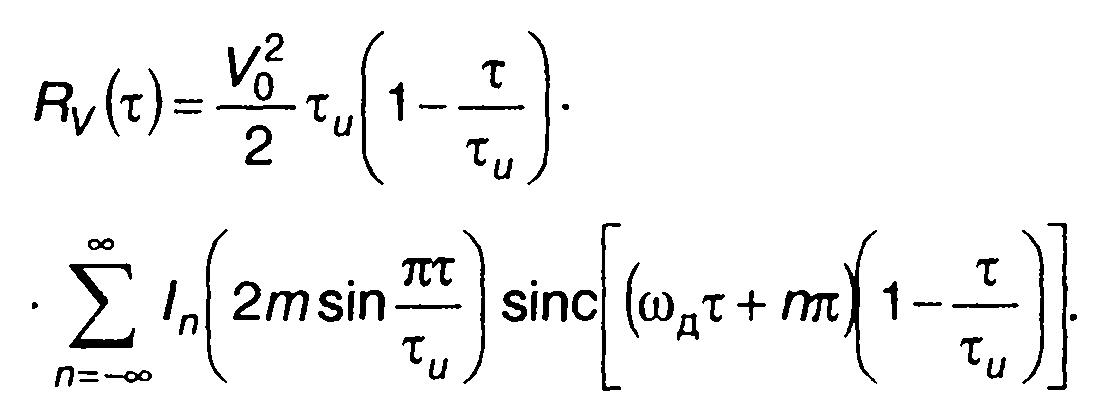(11.155)

Для малых значений τ << τ_и выражение для R_v(т) может быть упрощено

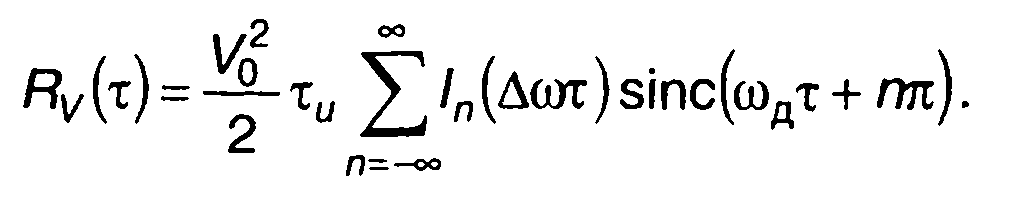(11.156)

Графики модуля корреляционной функции комплексной оги­бающей сигнала, построенные для различных ∆ω, приведены на рис. 11.22 и рис. 11.23 (на рис. 11.22 при ∆ω < 0 , на рис. 11.23 при ∆ω > 0). Модуль корреляционной функции имеет характерную ле­пестковую структуру, которая изменяется при изменении как знака, так и абсолютного значения ∆ω. При достаточно больших значе­ниях (по абсолюной величине) ∆ω > 0 лепестковая структура на­рушается.