ДЕТЕРМИНИРОВАННЫЕ СИГНАЛЫ 10 страница

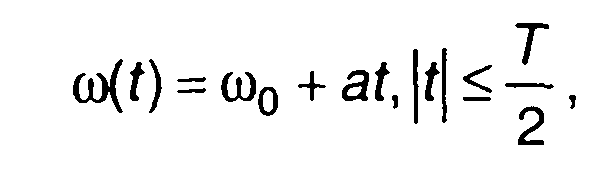(10.45)

где a=(a ω_д)/2 ; ω_д, T- девиация и период изменения частоты.

Фаза сигнала

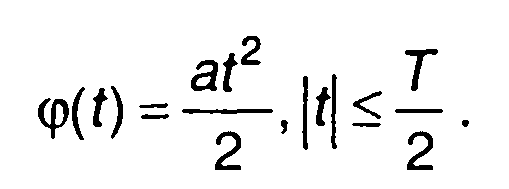(10.46)

Спектральная плотность комплексной огибающей импульсного ЧМ сигнала определяется выражением

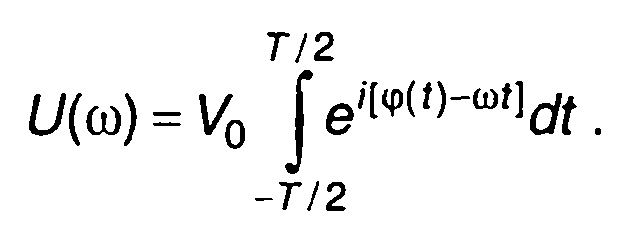(10.47)

Определение интеграла (10.47) через интегралы Френеля дано в разд. 11

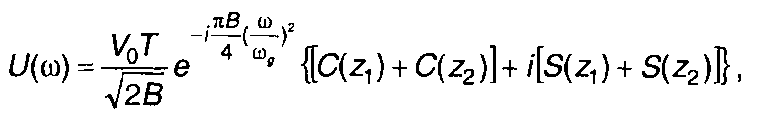(10.48)

где В =(ω_дT)/π=(2ω_д)/Ω; C(z), S(z) - интегралы Френеля;

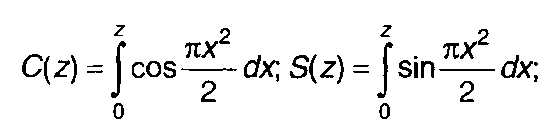(10.49)

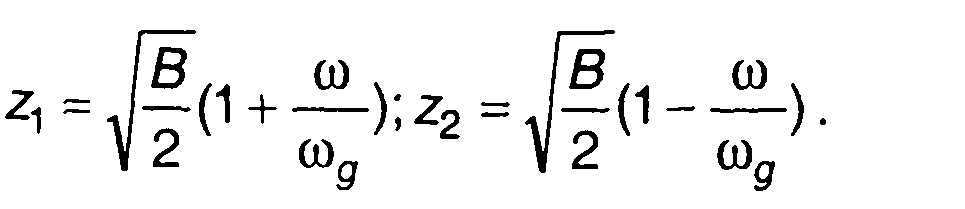(10.50)

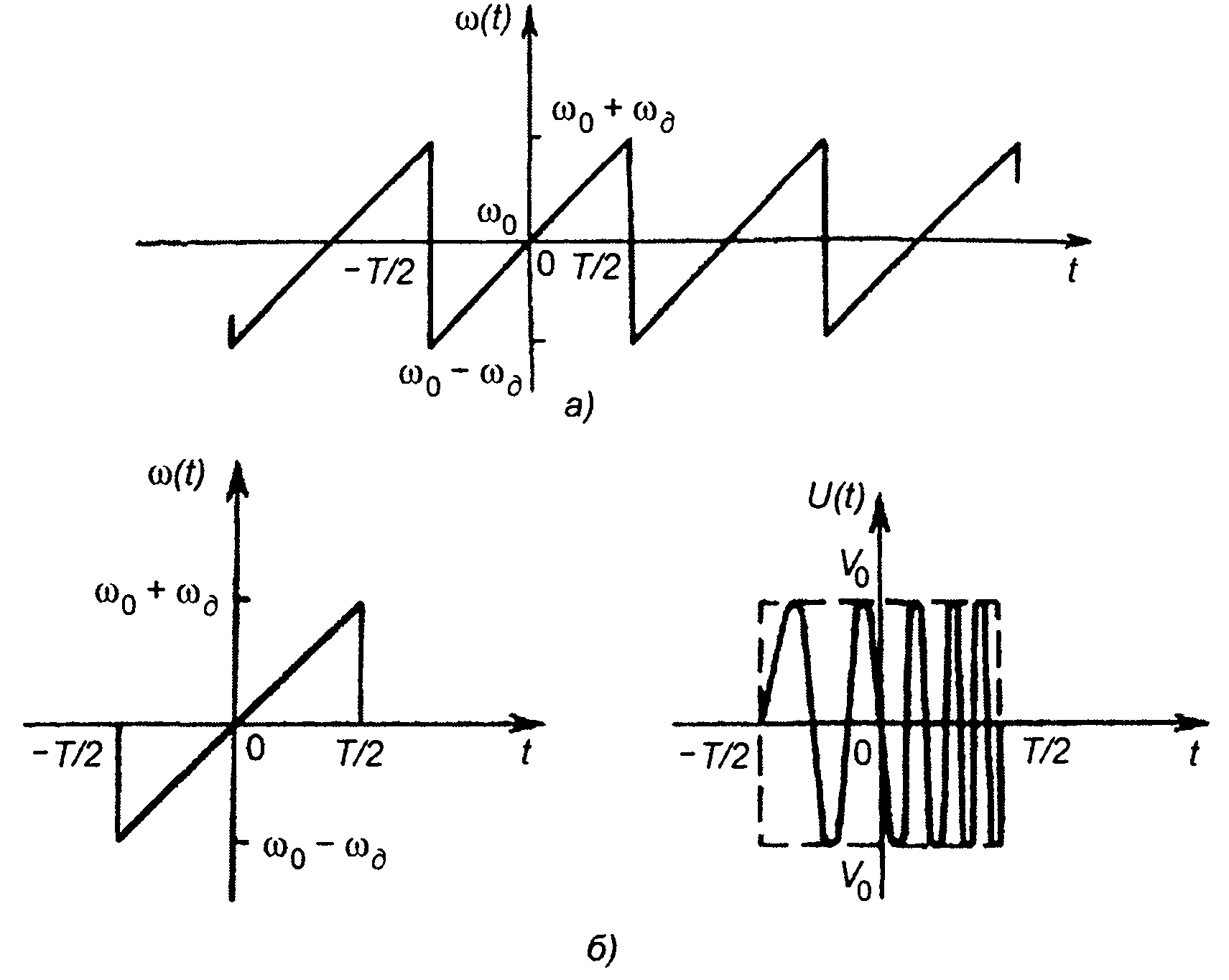
Рис. 10.14

Спектральная плотность импульсного ЧМ сигнала S(ω) опреде­ляется через спектральную плотность его комплексной огибающей U(ω) соотношением (разд. 8)

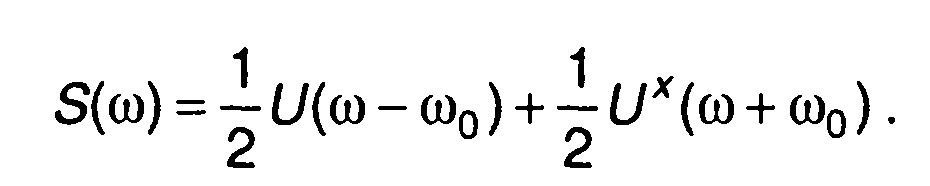(10.51)

Для ω > 0

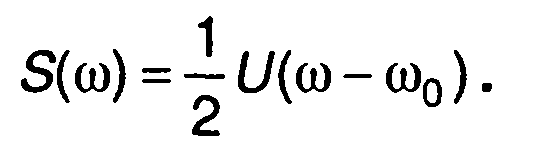
Переход от спектра импульсного сигнала к спектру периодиче­ской последовательности импульсов описан в разд. 3. Комплексный коэффициент ряда Фурье Сn связан со спектральной плотностью одиночного импульса равенством

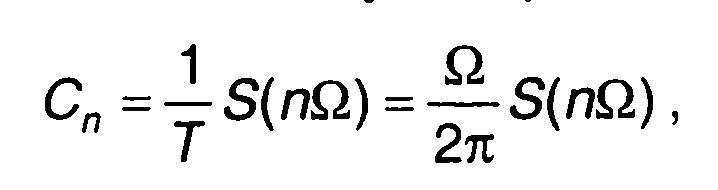(10.52)

где Ω, Т- частота и период модуляции.

Графики спектров периодического ЧМ сигнала с пилообразным несимметричным законом модуляции при различных значениях ин­декса модуляции m приведены на рис. 10.15.

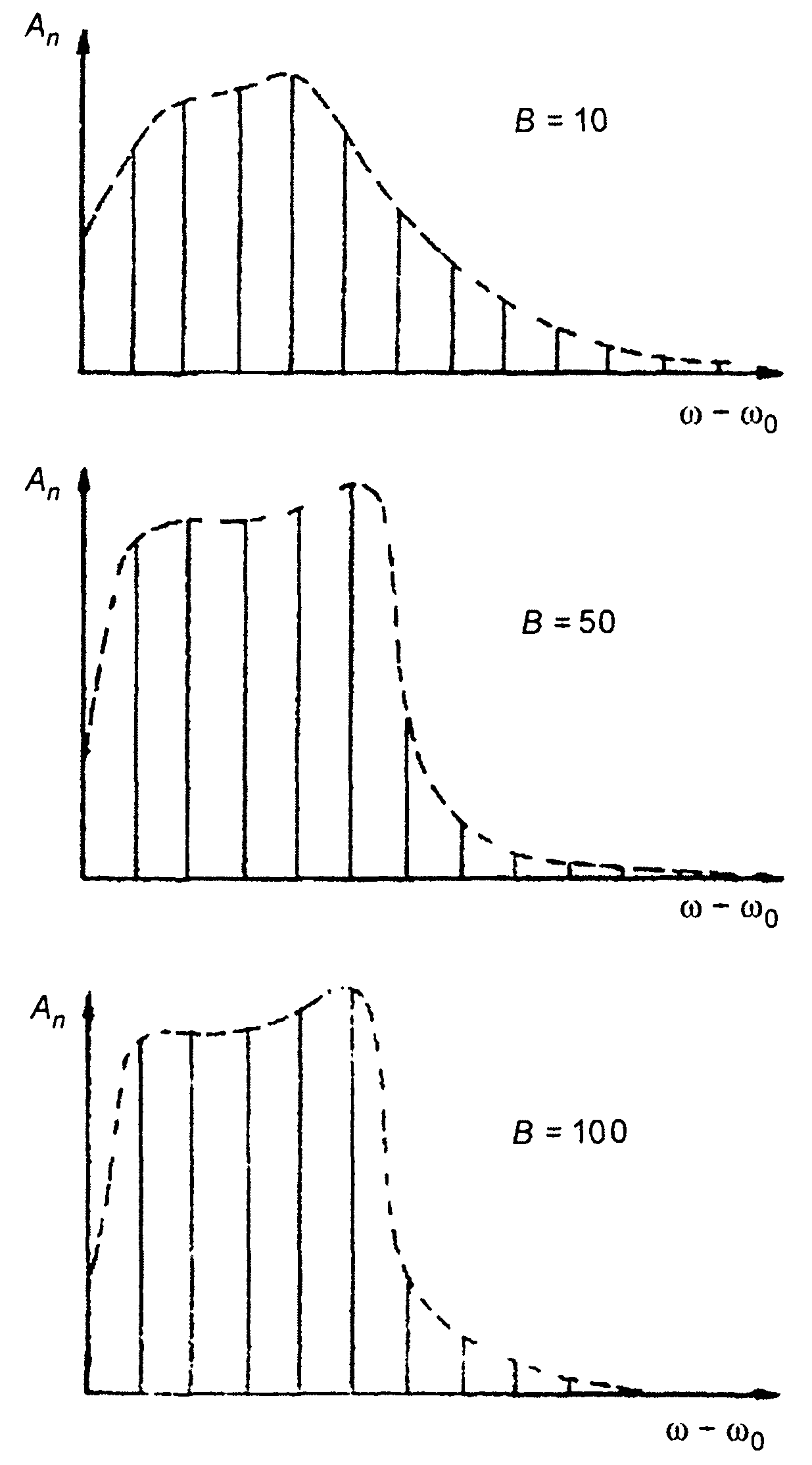
Рис. 10.15

Спектры дискретные, интервал дискретизации равен частоте модуляции Ω = 2π/T. Пунктирной линией изображены огибающие спектров. Спектры симметричны относительно несущей частоты ω_о, поэтому графики приведены только для ω > ω₀.

10.3.4.ЧМ сигнал с пилообразным симметричным законом модуляции

График зависимости частоты сигнала от времени изображен на рис. 10.16,а. Чтобы получить спектр периодического сигнала с таким законом ЧМ, рассмотрим импульсный сигнал с внутриимпульсной ЧМ, длительность которого равна периоду модуляции непрерывного сигнала (рис. 10.16,б). Частоту такого сигнала определим как

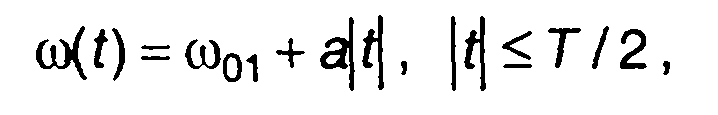(10.53)

где а = (4ω_д)/T; ω_д- девиация, ω₀₁ = ω₀ - ω_д.

Фаза сигнала описывается выражением

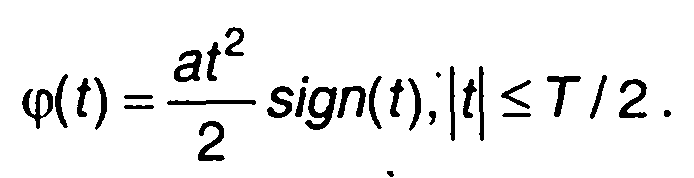(10.54)

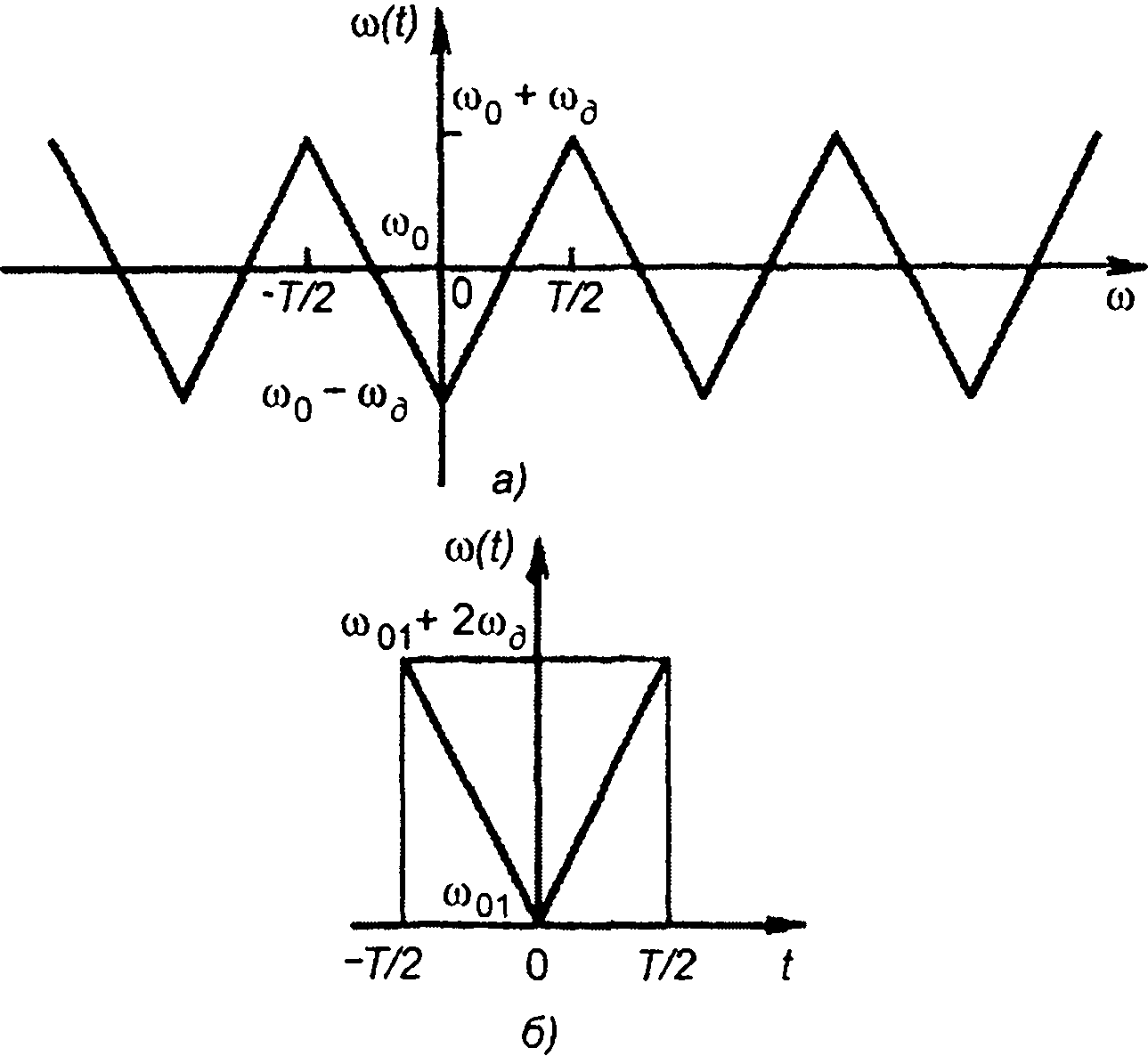
Рис. 10.16

Спектральная плотность комплексной огибающей сигнала опре­деляется выражением

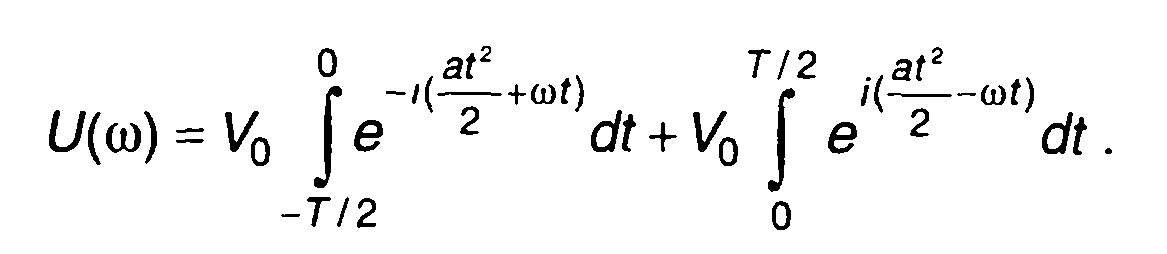(10.55)

Решение интеграла имеет вид (разд. 11)

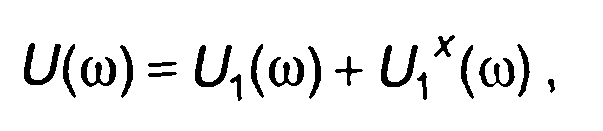(10.56)

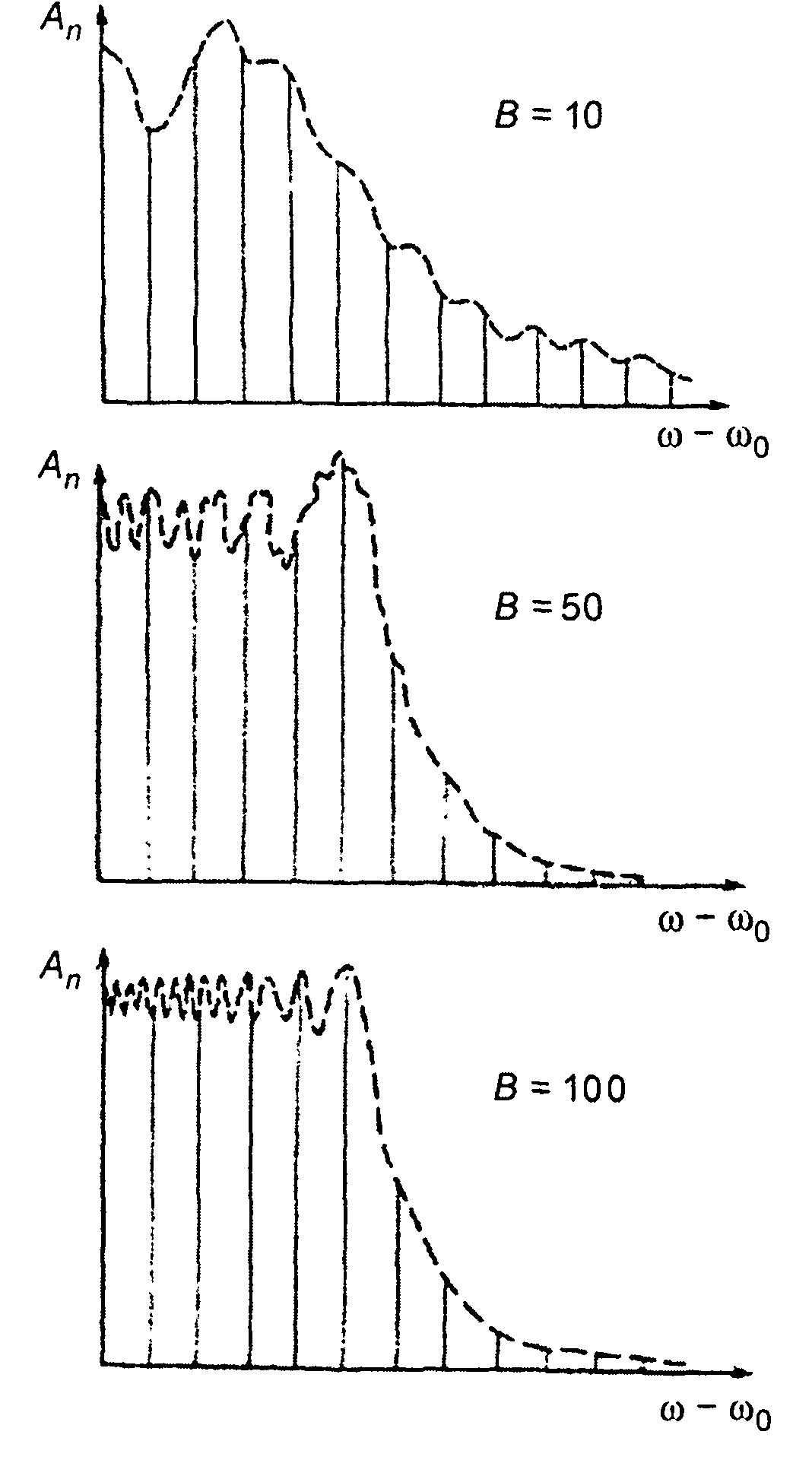
Рис. 10.17

где

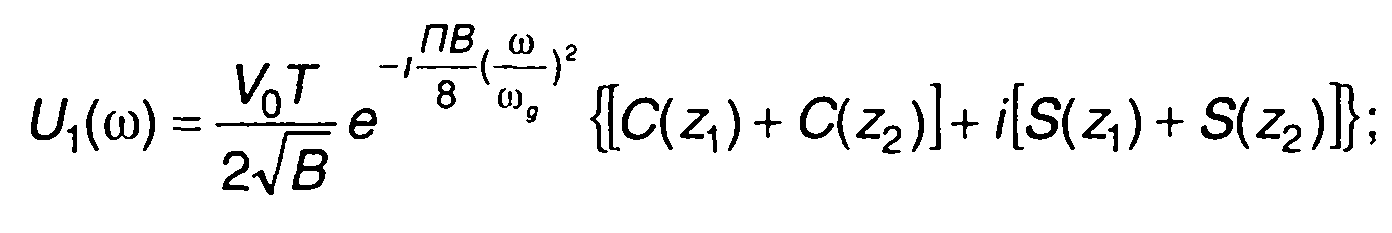(10.57)

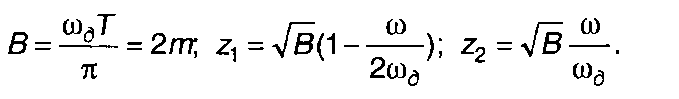(10.58)

Выражение (10.56) запишем в виде (разд. 11)

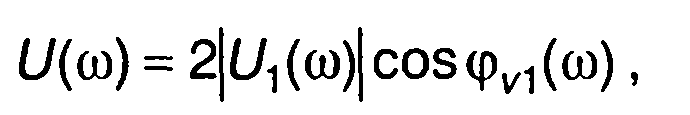(10.59)

где |U₁(ω)|, φ_v1(ω) - модуль и аргумент U₁(ω).

Спектральная плотность импульсного ЧМ сигнала для ω > 0 оп­ределяется как

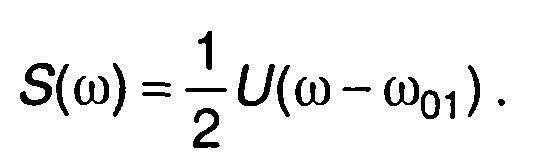(10.60)

Комплексные коэффициенты ряда Фурье, описывающие спектр непрерывного ЧМ сигнала, равны

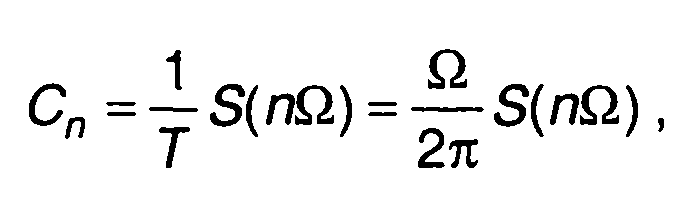(10.61)

где Ω, T- частота и период модуляции.

Графики амплитудных спектров ЧМ сигнала с симметричным пилообразным законом модуляции приведены на рис. 10.17. Они получены по результатам расчета спектров импульсных ЧМ сигна­лов (разд. 11). Пунктирной линией изображена огибающая спектра импульсного сигнала, дискреты показаны условно.

Раздел 11.

ИМПУЛЬСНЫЕ СИГНАЛЫ С ЧАСТОТНОЙ МОДУЛЯЦИЕЙ

Импульсные сигналы с внутриимпульсной ЧМ находят широкое применение в радиолокации, связи, измерительной технике и дру­гих областях. Привлекли они внимание прежде всего в связи с по­исками способов сжатия импульсных радиолокационных сигналов, что позволяет повысить разрешающую способность систем. Им­пульсные сигналы с линейной ЧМ (ЛЧМ) были первыми сигналами такого вида, их сжатие осуществляется с помощью согласованных фильтров.

Стремление к улучшению вида сигнала на выходе согласован­ного фильтра стимулировало исследования более сложных сигна­лов с нелинейной ЧМ (НЧМ). Указанные виды импульсных ЧМ сиг­налов и рассматриваются в дальнейшем - ЛЧМ и НЧМ сигналы, даются их описание и характеристики.

11.1. Описание ЛЧМ сигналов

Импульсный ЧМ сигнал в общем случае описывается выражени­ем

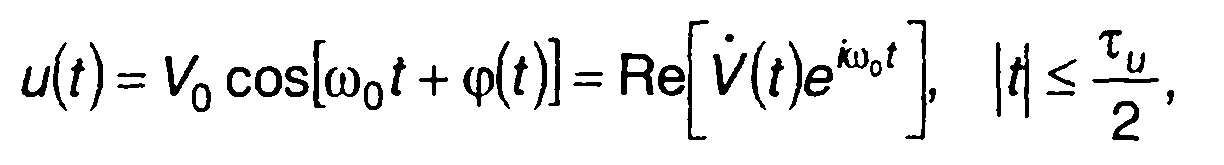(11.1)

где V₀, ω₀, φ(t), τ_u - амплитуда, несущая частота, фаза и длитель­ность сигнала; V(t)=V₀e^iφ(t) - комплексная огибающая сигнала.

Мгновенная частота сигнала

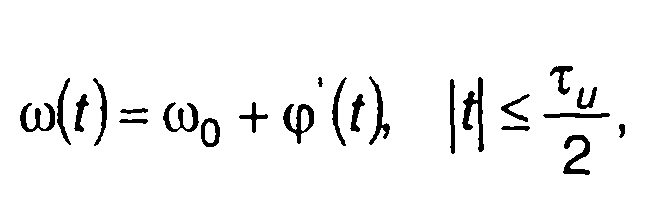(11.2)

Где φ’(t) переменная составляющая частоты.

Функция ω(t) описывает закон изменения частоты во времени - закон модуляции.

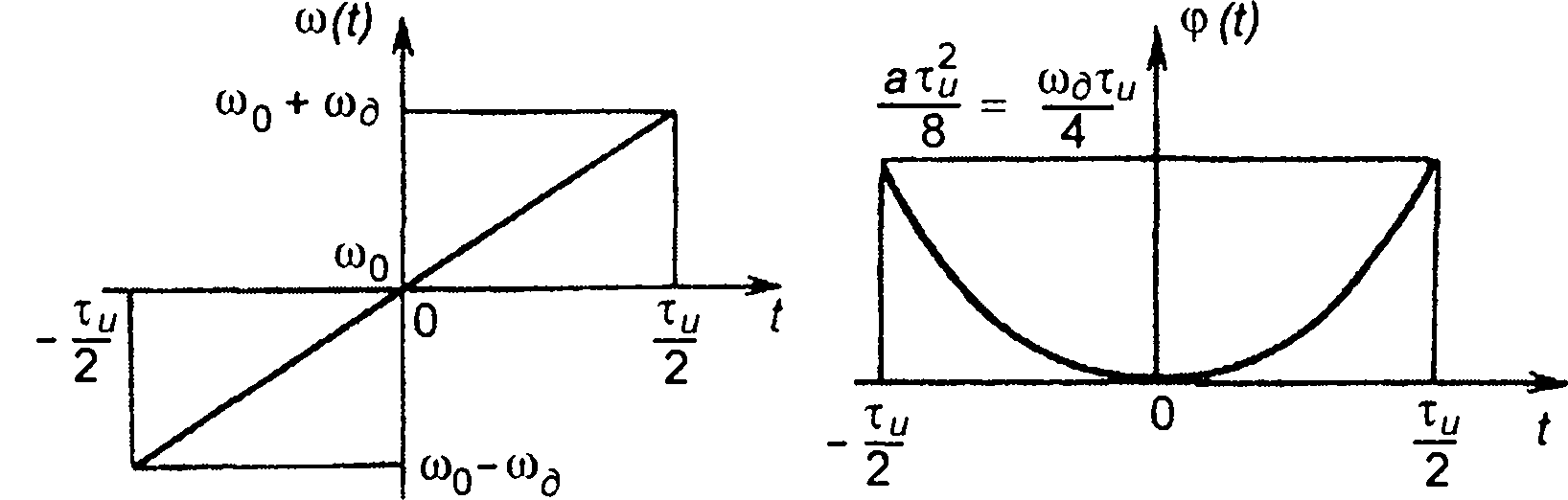
Рис. 11.1

Обычно формируются ЛЧМ сигналы, имеющие нечетную сим­метрию функции ω(t) относительно ω₀ (рис. 11.1)

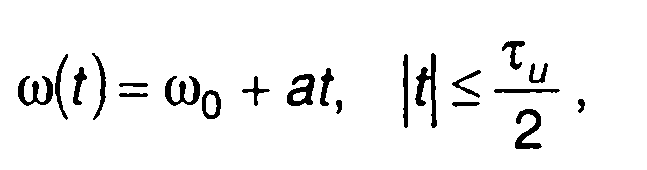(11.3)

где а = 2ω_д/т_u; ω_д - девиация частоты.

Фаза сигнала (рис. 11.1)

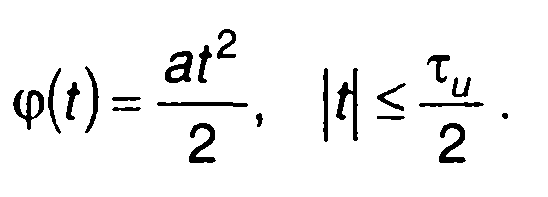(11.4)

Возможна четная симметрия закона модуляции (рис. 11.2)

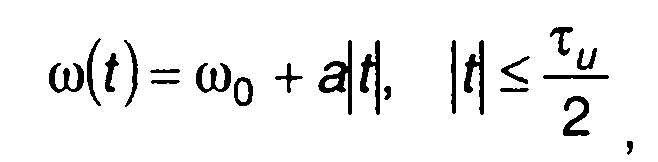(11.5)

При четной симметрии фаза сигнала

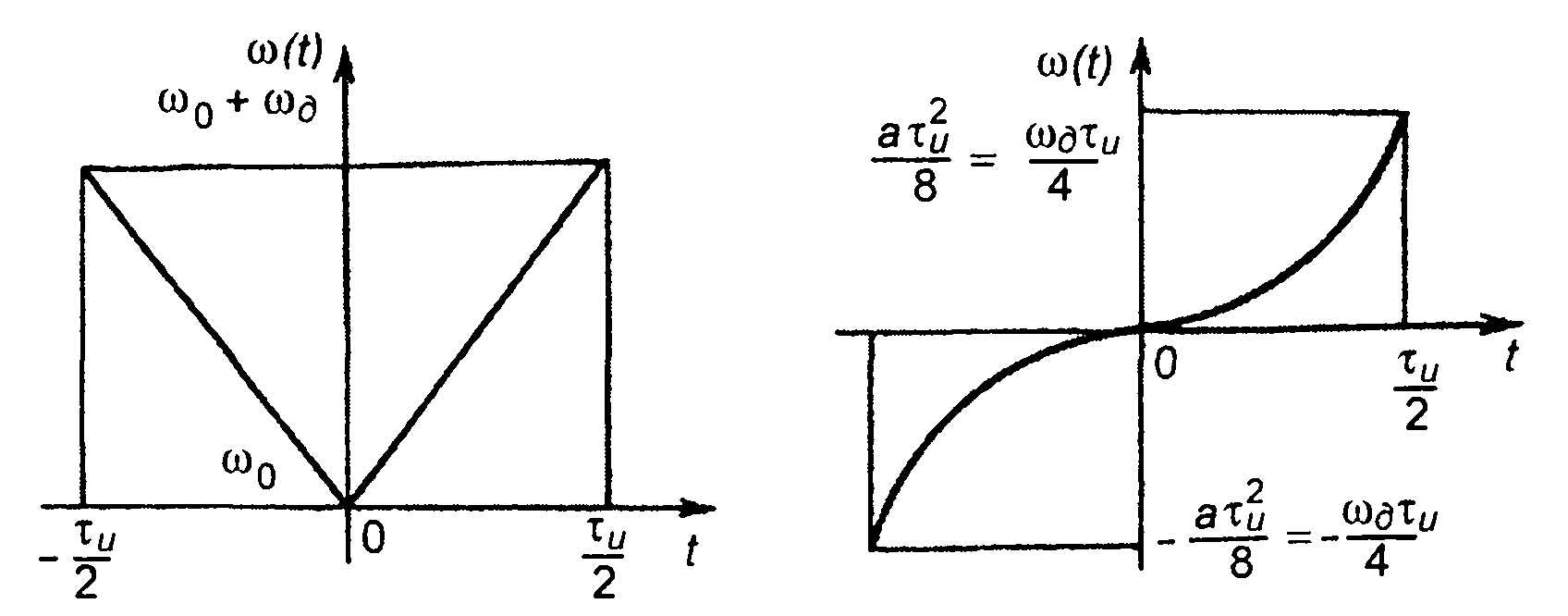
Рис. 11.2

Раздел 11

(11.6)

где

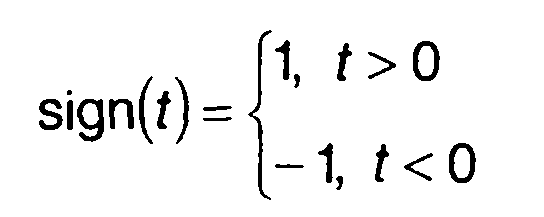
Зависимость ω(t) (или φ(t)) для нечетного или четного законов ЛЧМ полностью определяют характеристики сигналов - спектр и корреляционную функцию.

11.2. Спектр ЛЧМ сигнала с нечетносимметричным законом модуляции

Спектр ЛЧМ сигнала S(co) удобнее определять через спектр его комплексной огибающей U(ω) (разд. 8)

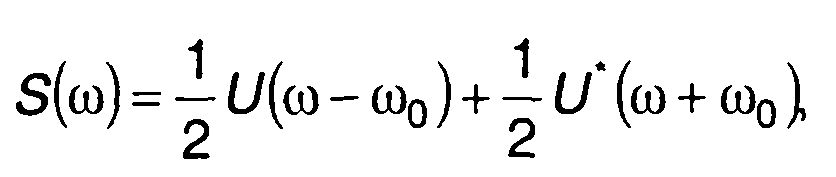(11.7)

где

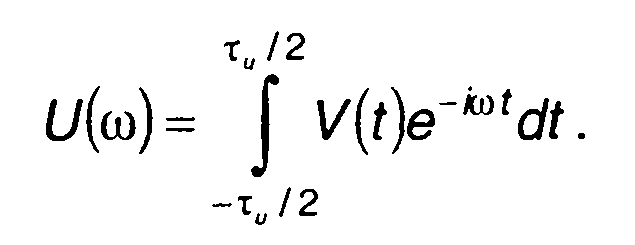(11-8)

Подставляя в (11.8) V(t) = V₀e^iφ(t), выражение для спектральной плотности комплексной огибающей с учетом (11.4) запишем в виде

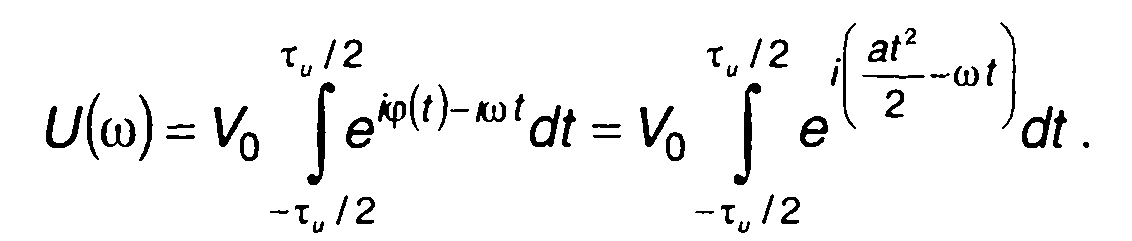(11.9)

Используя интегралы Френеля

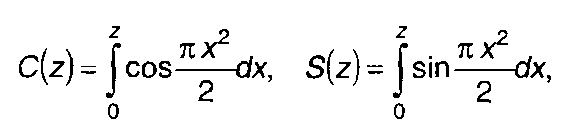(11.10)

из (11.9) получаем

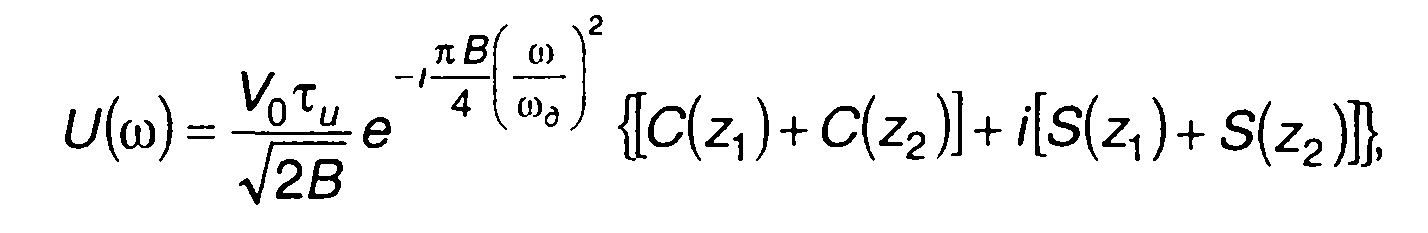(11.11)

где

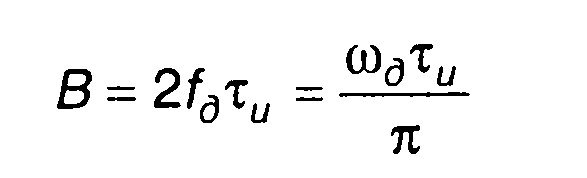
- база сигнала;

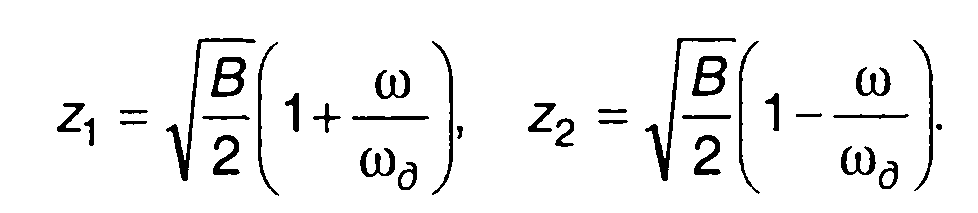(11.12)

Амплитудный спектр комплексной огибающей сигнала описыва­ется выражением

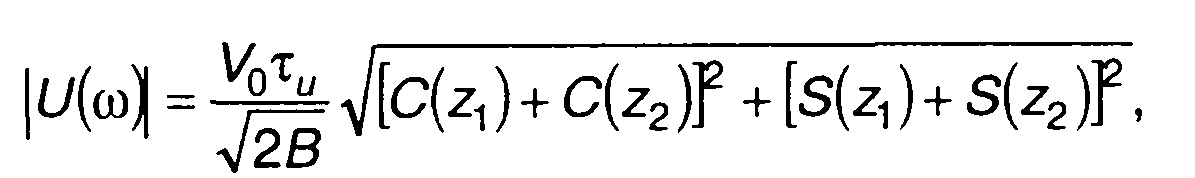(11.13)

фазовый спектр

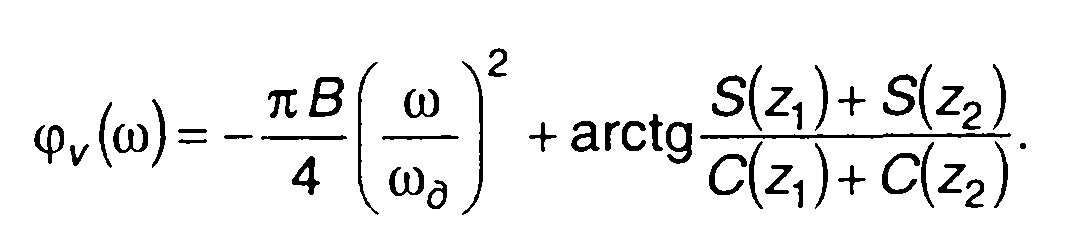(11.14)

Для сигналов с большим значением базы (В>>1) при ω = 0 (z₁ = z₂) можем принять

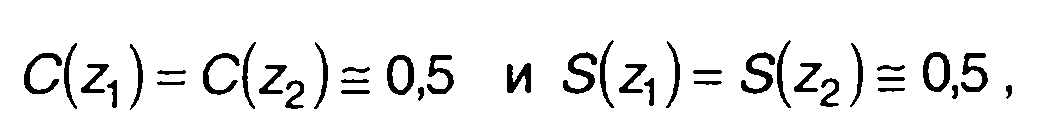(11.15)

С учетом (11.15) из (11.13) получим

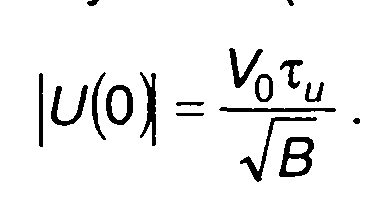(11.16)

При ω = ω_д

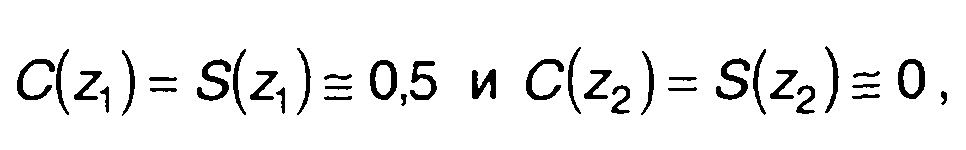(11.17)

из (11.13) найдем

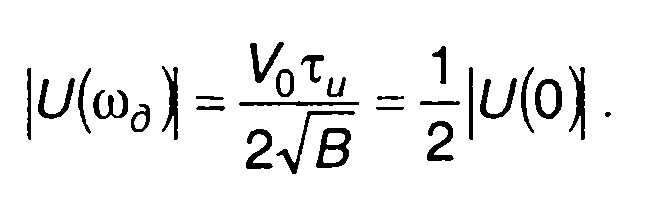(11.18)

Таким образом, можно считать, что при больших значениях ба­зы ширина спектра равна удвоенному значению девиации частоты.

Выражение для спектра комплексной огибающей сигнала (11.9) представим в виде

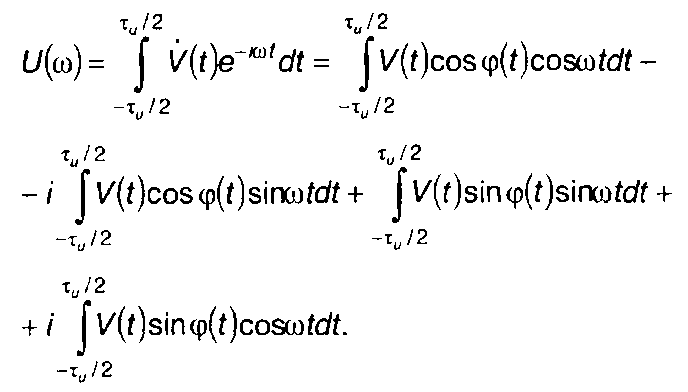(11.19)

При нечетной симметрии закона модуляции, как следует из (11.4), фаза является четной функцией времени, т.е.

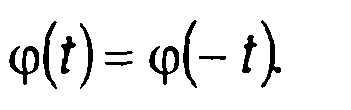
Учтем также, что произведение двух четных или двух нечетных функций дает четную функцию, а произведение четной функции и нечетной - нечетную. Для нечетной функции интеграл в симметричных относительно нуля пределах равен нулю. Таким образом, в (11.19) второй и третий интегралы равны нулю. Выражение для U(ω) запишется в виде:

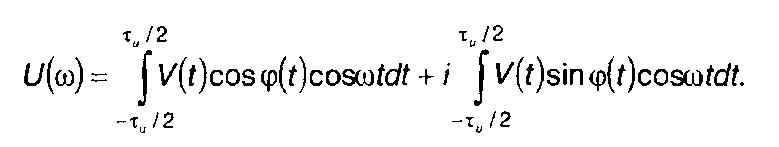(11.20)

Функция U(ω) является четной

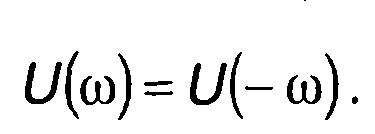(11.21)

Четными функциями частоты являются амплитудный и фазовый спектры

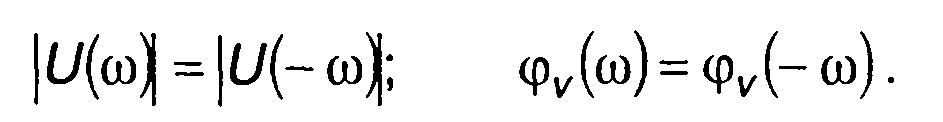(11.22)

О характере амплитудного спектра сигнала можно судить по гра­фикам, приведенным на рис. 11.3 для различных значений базы В. Так как амплитудный спектр является четной функцией частоты,

графики приведены только для ω>0. Как следует из анализа гра­фиков, амплитудный спектр при достаточно больших значениях базы является довольно равномерным в полосе частот, ограни­ченной значениями |ω_д|, быстро спадает за пределами указанной

полосы, амплитуда пульсаций спектра уменьшается при увеличе­нии базы сигнала В.

11.3. Приближенное определение спектра ЛЧМ сигнала

Упрощение расчета и анализа спектра ЧМ сигнала дает метод стационарной фазы. Он основан на использовании приближенного решения интеграла вида

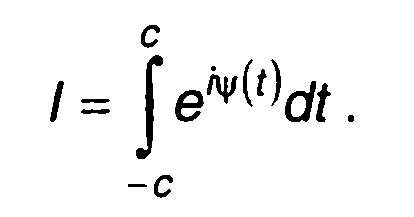(11.23)

Значение интеграла (11.23) в основном определяется интерва­лом, на котором скорость изменения колебаний, описываемых подинтегральной функцией, является минимальной. Этот интервал определяется окрестностью той точки, в которой функция ψ(t) ста­ционарна или скорость ее изменения ψ (t) минимальна. Функция ψ(t) представляет фазу колебания, поэтому описываемый метод называется методом стационарной фазы.

Минимальное значение ψ` (t) будет около точки, которая нахо­дится из уравнения

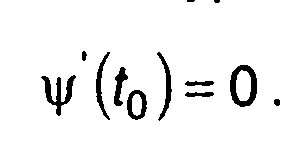(11.24)

Раскладывая ψ(t) в ряд Тейлора в окрестности точки t₀ и огра­ничиваясь в разложении двумя первыми слагаемыми, запишем

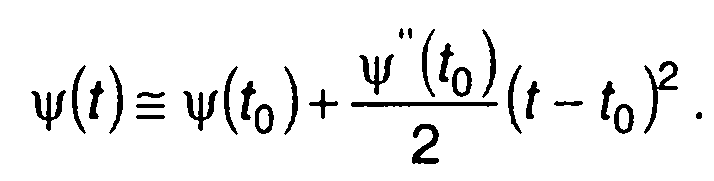(11.25)

Подставляя (11.25) в (11.23), получаем

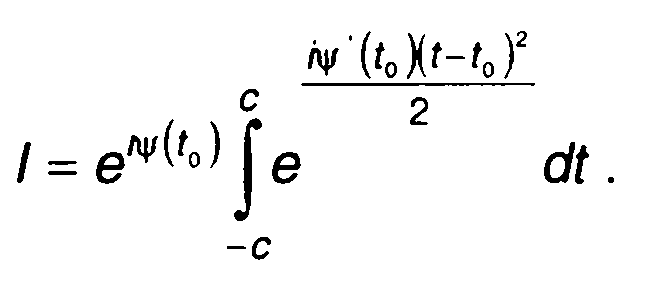(11.26)

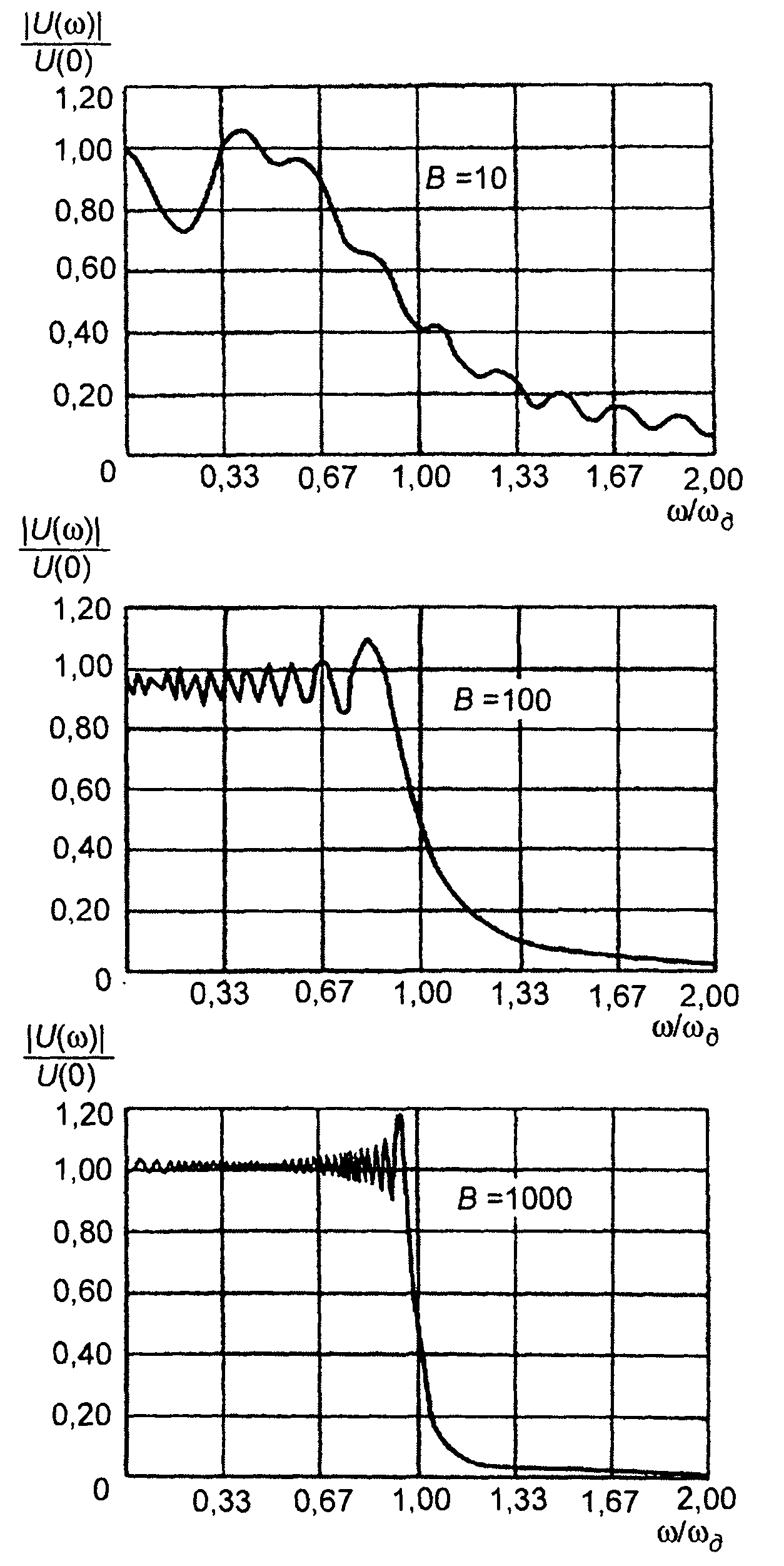
Рис. 11.3

Как правило, замена пределов интегрирования в (11.26) на ±∞ не оказывает заметного влияния на результат и в рамках прини­маемых допущений вполне оправдана. С учетом известного равен­ства

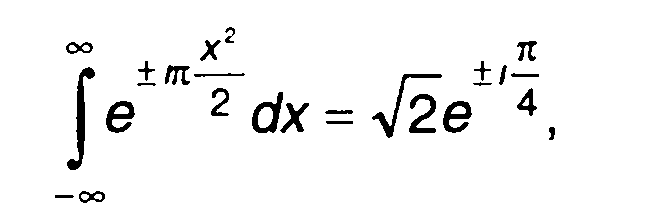(11.27)

из (11.26) получим

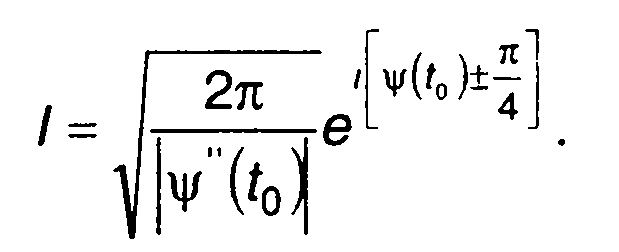(11.28)

Знак перед π/4 в показателе степени совпадает со знаком ψ`` (t₀). Если уравнение (11.24) имеет несколько решений, то инте­грал (11.28) равен сумме интегралов, взятых для каждого из реше­ний.

Используя метод стационарной фазы, описанный выше, опре­деляем спектральную плотность комплексной огибающей ЛЧМ сиг­нала, описываемую (11.9). Интеграл в (11.9) идентичен (11.23) при

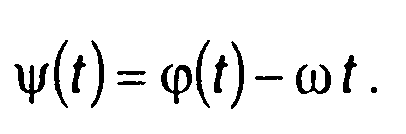(11.29)

Равенство, из которого определяется точка стационарной фазы, имеет вид

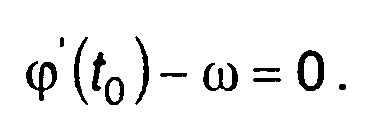(11.30)

С учетом выражения для φ(t) получим

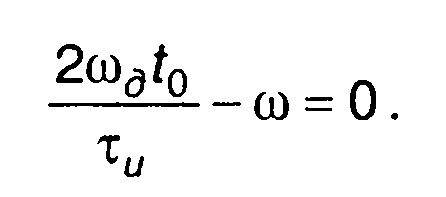(11.31)

Точка стационарной фазы равна

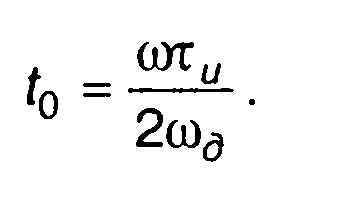(11.32)

Таким образом, имеем

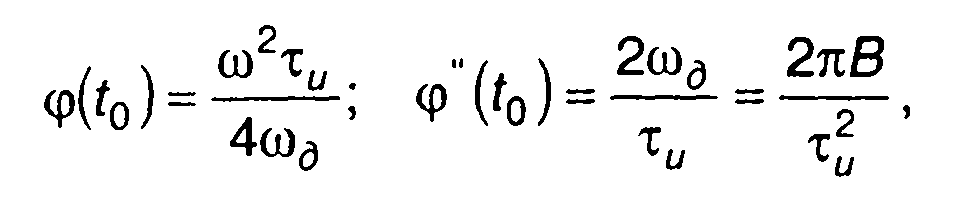(11.33)

спектральная плотность описывается выражением

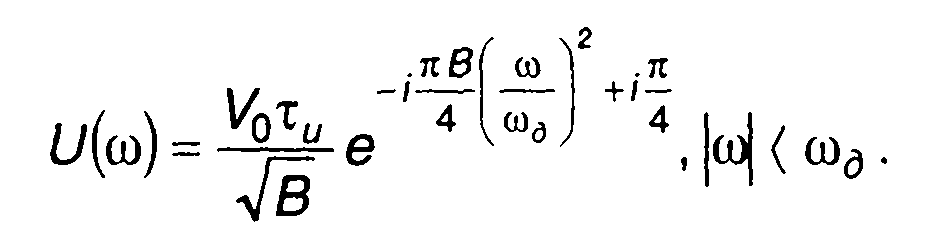(11.34)

Амплитудный спектр

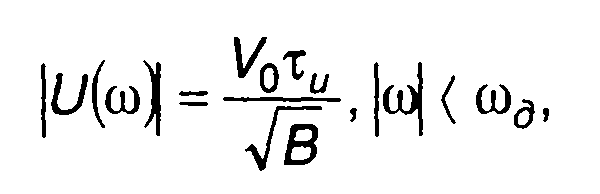(11.35)

что совпадает c (11.16).

11.4. Спектр пачки импульсов с внутриимпульсной ЛЧМ

Пачка радиоимпульсов с внутриимпульсной ЧМ описывается выражением

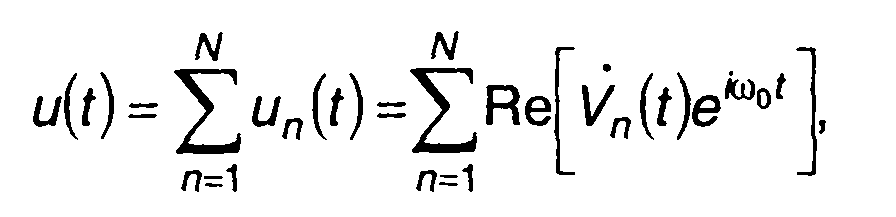(11.36)

где V_n(t) - комплексная огибающая л-го импульса;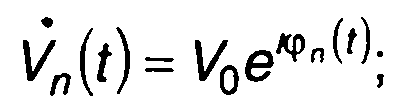

V₀,ω₀,φ_n(t) - амплитуда, несущая частота и фаза колебания n-го импульса.

Как узкополосный сигнал u(t) может быть представлен в виде

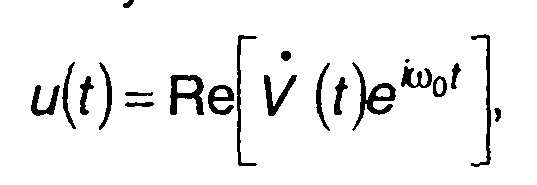(11.37)

где V(t)= \/₀е^iφ(t) - комплексная огибающая сигнала; φ(t) - фаза сигнала.

Из равенства (11.36) и (11.37) получим

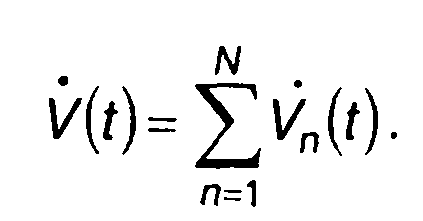(11.38)

Как следует из (11.38), спектральная плотность комплексной огибающей пачки импульсов определяется суммой спектральных плотностей импульсов, входящих в состав пачки. Спектральную

плотность комплексной огибающей любого из N идентичных им­пульсов с внутриимпульсной ЧМ определим как спектральную плотность комплексной огибающей первого импульса, умноженную на множитель смещения (разд. 3)

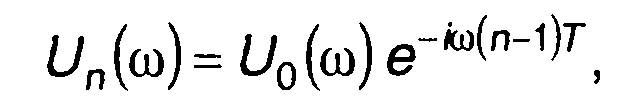(11.39)

где U₀ (ω) - спектральная плотность комплексной огибающей пер­вого импульса; Т - период следования импульсов в пачке.

С учетом (11.39) из (11.38) получим

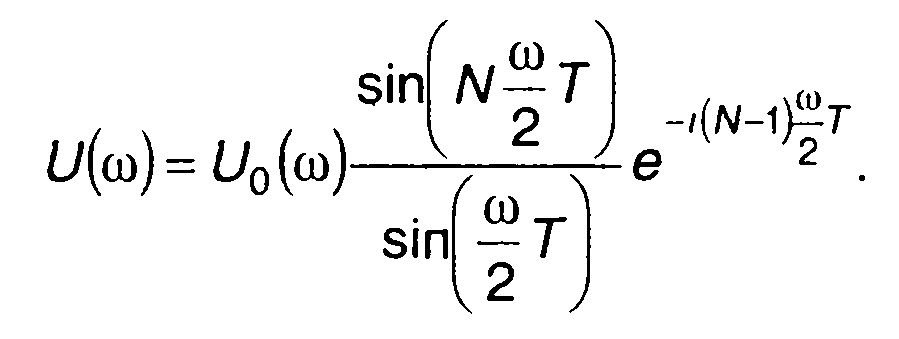(11.40)

Таким образом, спектральная плотность комплексной огибаю­щей пачки из N радиоимпульсов с внутриимпульсной ЧМ получает­ся умножением спектральной плотности комплексной огибающей одиночного импульса на множитель

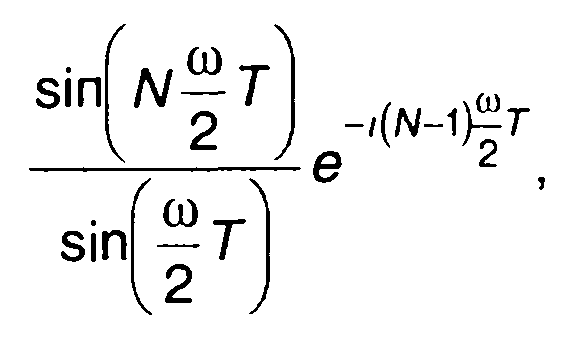(11.41)

учитывающий число импульсов и период их следования в пачке.

При нечетносимметричном законе ЛЧМ функция U₀(ω) описыва­ется (11.11). На рис. 11.4, 11.5 представлены графики амплитудных спектров комплексной огибающей пачки импульсов с внутриим­пульсной ЛЧМ для базы сигнала В = 100 и различных значений па­раметров: N и q = T/τ_u, где τ_и - длительность импульса, Т - пери­од следования импульсов в пачке. На рис. 11.4,а и 11.5,а спектры приведены для достаточно широкого диапазона частот. Но структу­ра спектра такова, что из рис. 11.4,а и 11.5,а можно получить пред­ставление только об огибающей спектра. О структуре спектра можно судить по его фрагментам, выделенным для довольно узкой полосы частот - рис. 11.4,б и 11.5,б.

Переход от спектральной плотности комплексной огибающей к спектральной плотности сигнала определяется ранее приведен­ным выражением (11.7).

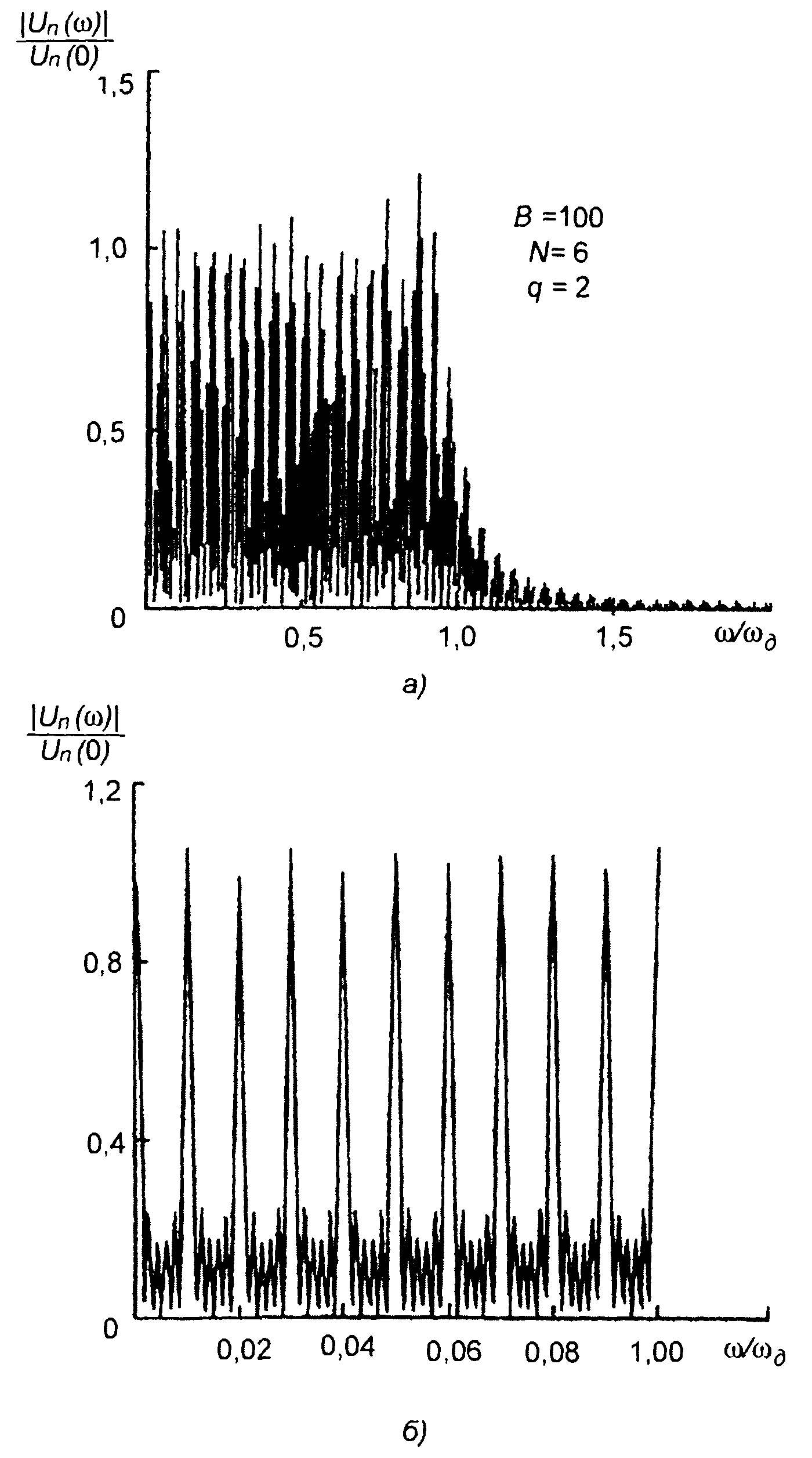
Рис. 11.4

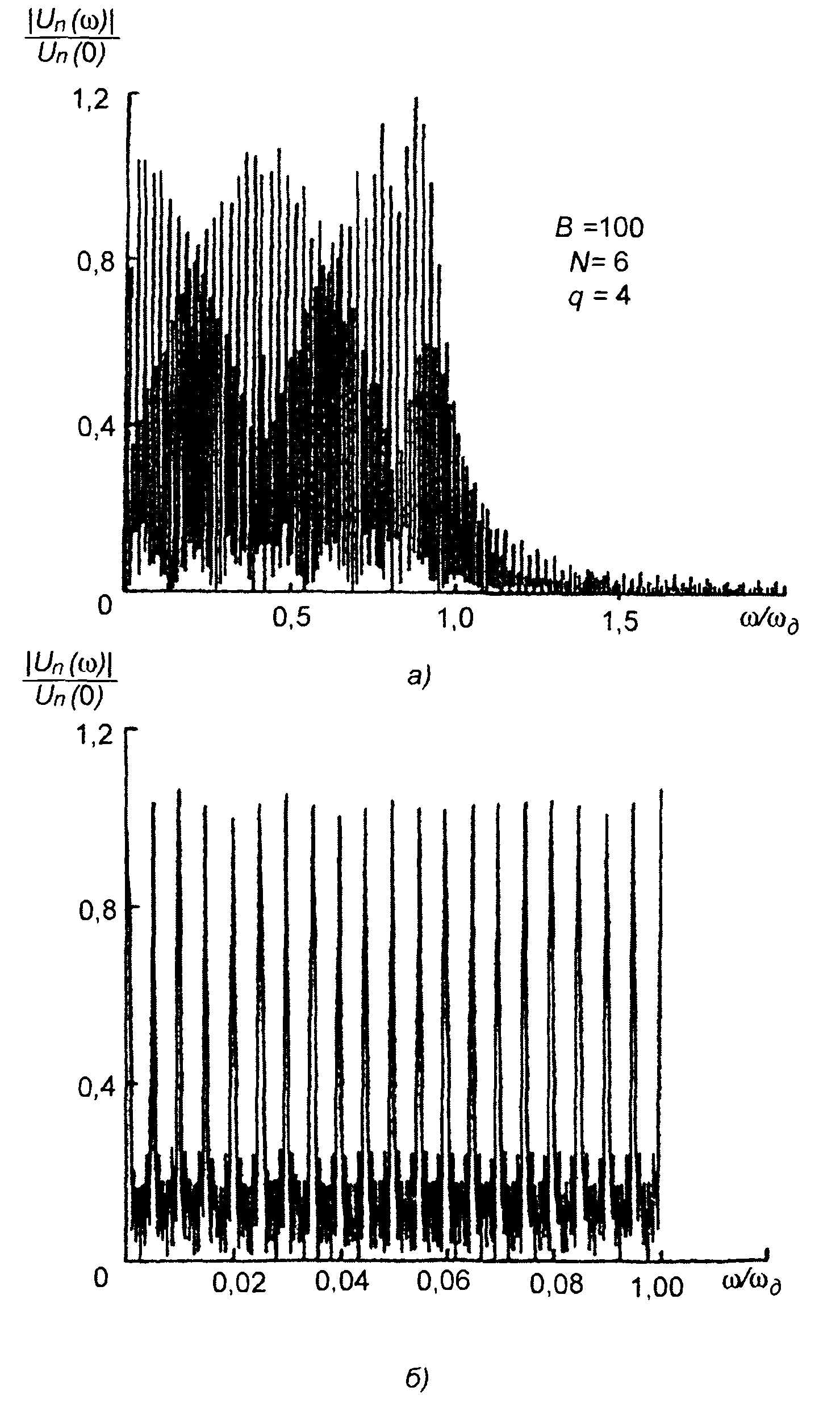
Рис. 11.5

11.5. Корреляционная функция ЛЧМ сигнала при нечет­ной симметрии закона модуляции

Корреляционная функция ЛЧМ сигнала связана с корреляцион­ной функцией его комплексной огибающей следующей соотноше­нием (разд. 8)

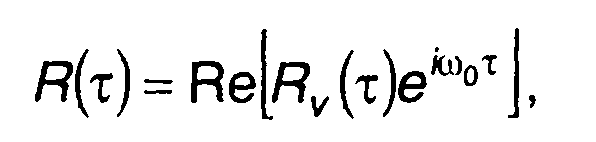(11.42)

где R_v(τ) - корреляционная функция комплексной огибающей сиг­нала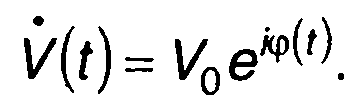

Корреляционная функция комплексной огибающей сигнала оп­ределяется выражением

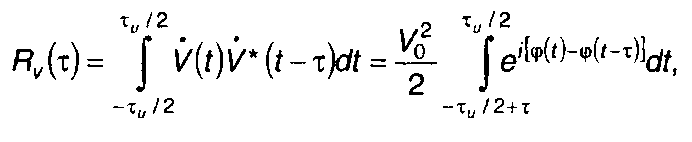(11.43)

где τ - смещение во времени.

Для ЛЧМ сигнала с учетом (11.4) запишем

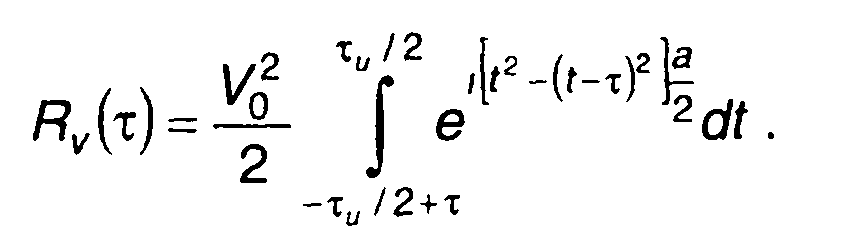(11.44)

Решая интеграл в (11.44), получим

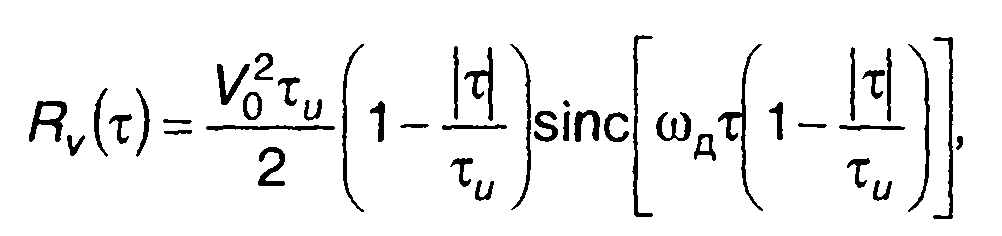(11.45)

где

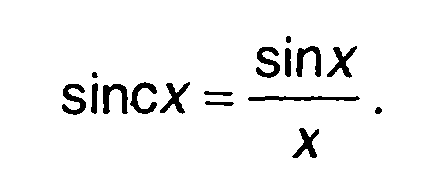
При малых значениях т << τ_и разность фаз в (11.43) может быть определена как

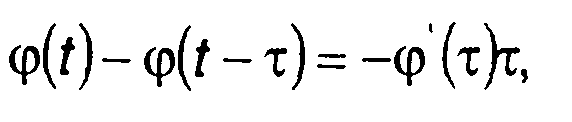(11.46)

а нижний предел интегрирования принят равным -τ_u/2. С учетом этого выражение для R_v(т) запишем в виде

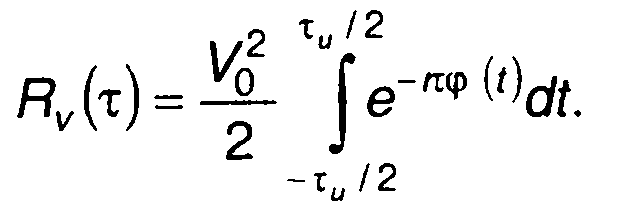(11.47)

Выражение (11.47) представим как

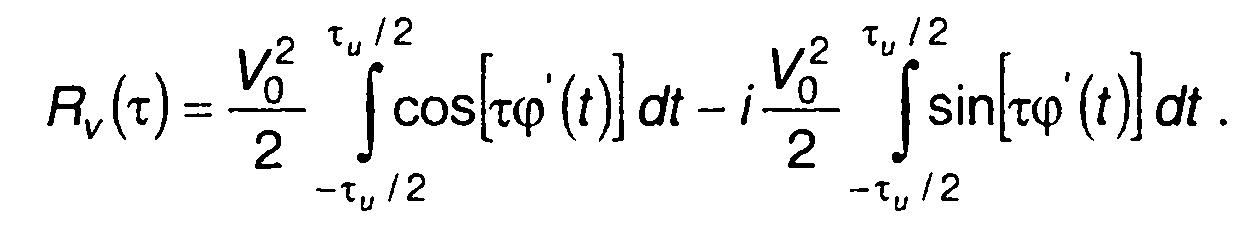(11.48)

Подынтегральное выражение первого слагаемого представляет четную функцию, второго слагаемого - нечетную функцию време­ни. Учитывая, что интеграл в симметричных пределах от четной функции равен удвоенному интегралу от нуля до верхнего преде­ла, а от нечетной функции равен нулю, выражение для R_v(т) мо­жем записать в виде

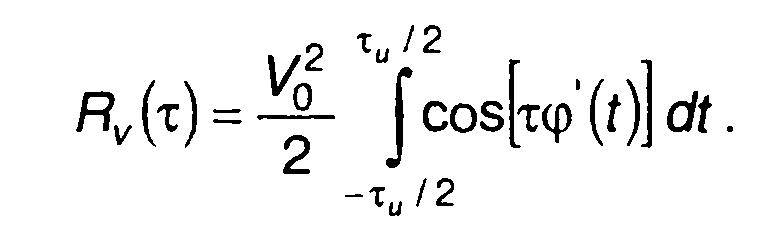(11.49)

С учетом равенства φ` (t) = at получим

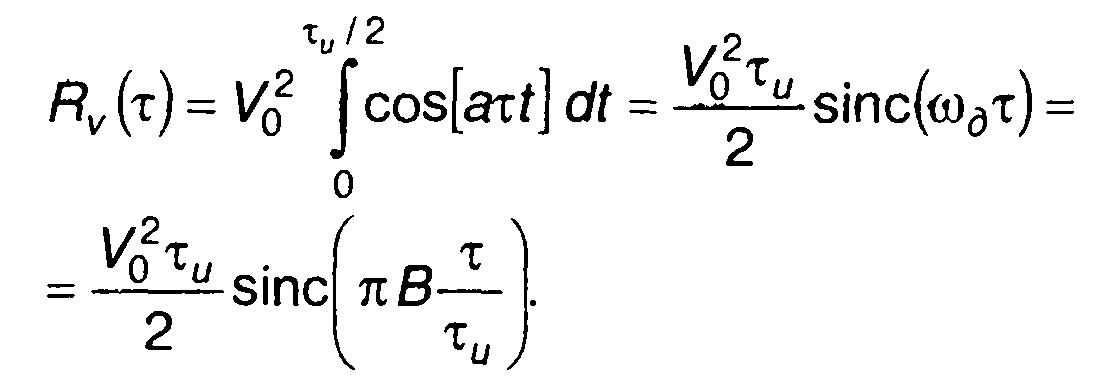(11.50)

К такому же результату придем исходя из (11.45), пренебрегая вторым слагаемым в круглых скобках. Как следует из (11.45) и (11.50) корреляционная функция имеет главный и боковые мак­симумы. Ширина главного максимума определяется из соотноше­ния

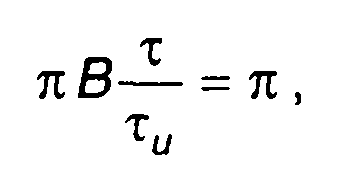(11.51)

и равна

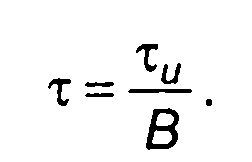(11-52)

Таким образом, при больших значениях В >> 1 ширина главного максимума значительно меньше длительности импульса и при­ближение, принятое при нахождении корреляционной функции (11.50), выглядит вполне оправданными. Отношение длительности сигнала к ширине главного максимума (корреляционного пика) на­зывается коэффициентом сжатия. Для рассматриваемого сигнала, как следует из приведенных соотношений, он равен базе сигнала В. Графики модуля корреляционной функции комплексной оги­бающей ЛЧМ сигнала для некоторых значений В приведены на рис. 11.6.

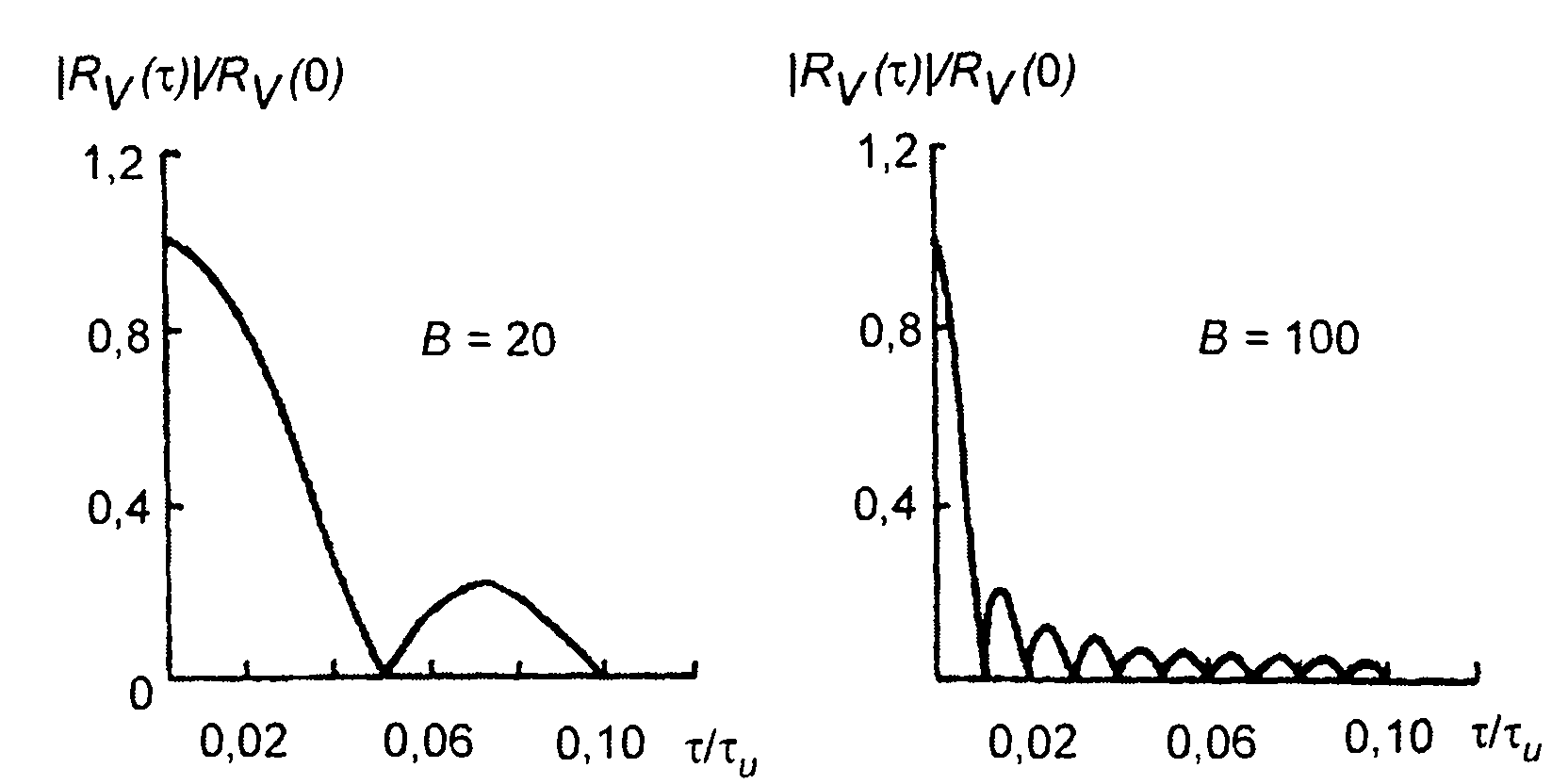
Рис. 11.6

11.6. Спектр и корреляционная функция ЛЧМ сигнала с четносимметричным законом модуляции

При четной симметрии закона модуляции выражение для спек­тральной плотности комплексной огибающей ЛЧМ сигнала (11.8) примет вид

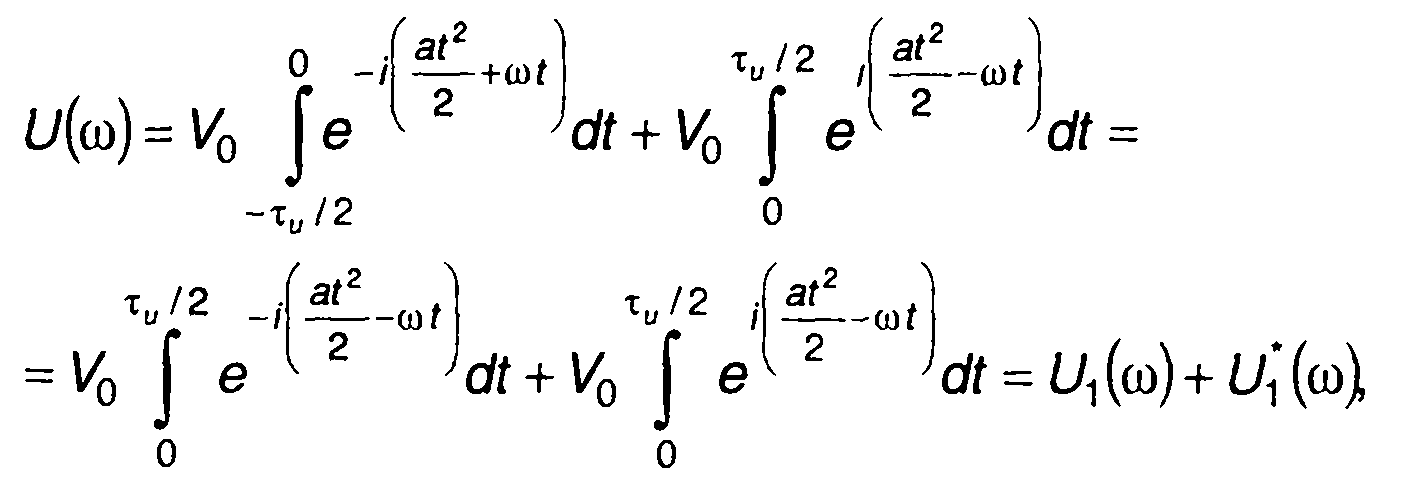(11.53)

где

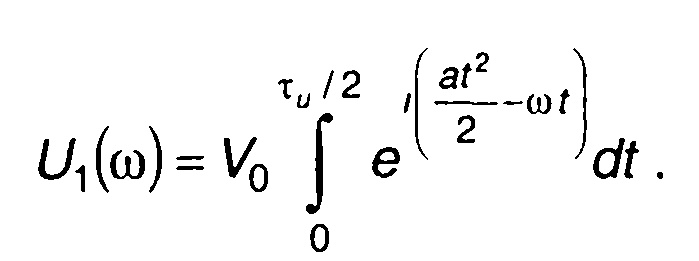(11.54)

Представим (11.53) в виде

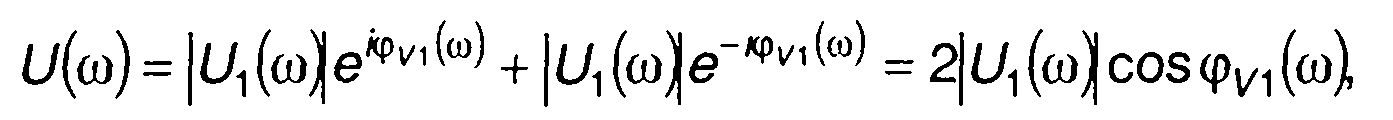(11.55)

где φ_v1(ω) - аргумент Ц(со).

Как следует из (11.55), спектральная плотность комплексной огибающей ЛЧМ сигнала является действительной функцией час­тоты. Чтобы определить ее, найдем U₁(ω).

По аналогии с (11.11) получим

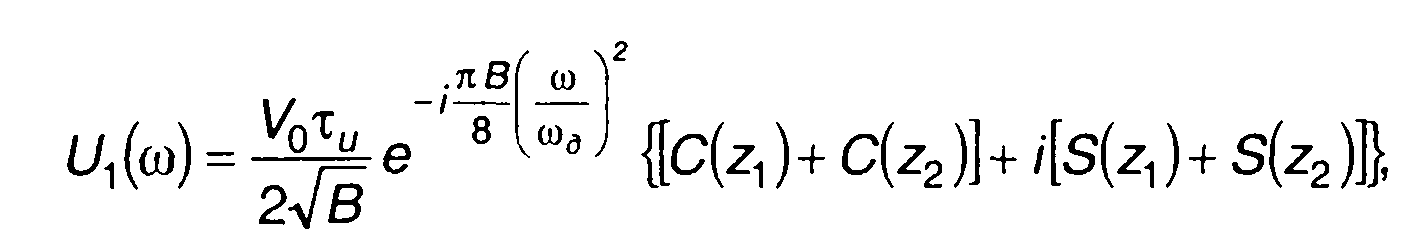(11.56)

где 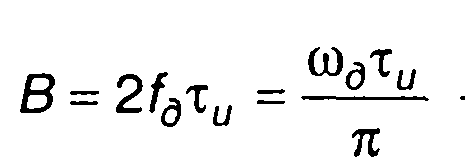- база сигнала; С(х), S(x) - интегралы Френе­ля;

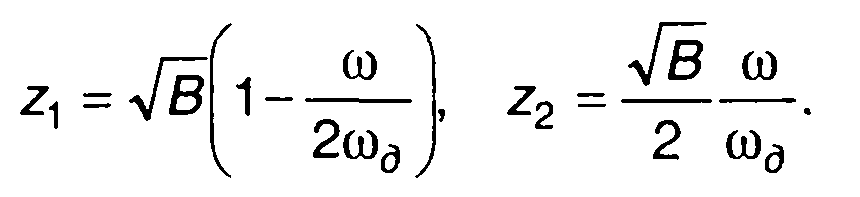
Модуль и аргумент U₁(ω) описываются выражениями

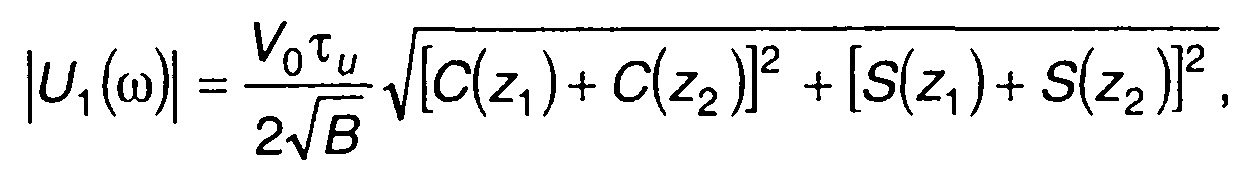(11.57)

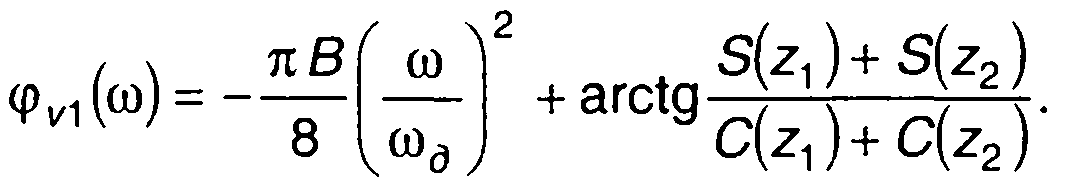(11.58)

С учетом (11.57) и (11.58) из (11.55) можно определить ампли­тудный и фазовый спектры комплексной огибающей сигнала

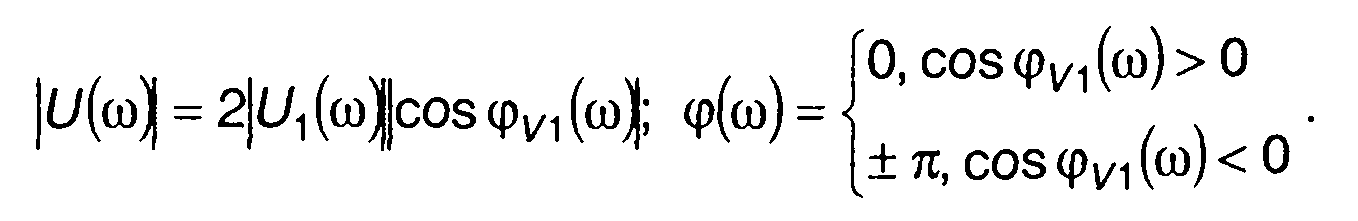(11.59)

Графики амплитудного спектра, рассчитанные по приведенным выражениям, изображены на рис.11.7-11.9. Амплитудный спектр описывается осциллирующей функцией (выражение для |U(ω)| со­держит косинус), поэтому его изображение не всегда возможно (особенно при больших значениях В). На рис. 11.8,а и 11.9.а пока­заны огибающие спектров. Характер осцилляций спектра иллюст­рируется рис. 11.8,б и 11.9,б, где даны фрагменты графиков спек­тров.

Характер спектра отражает и приближенное решение, получае­мое методом стационарной фазы. Асимптотическое выражение для спектра найдем с учетом равенства

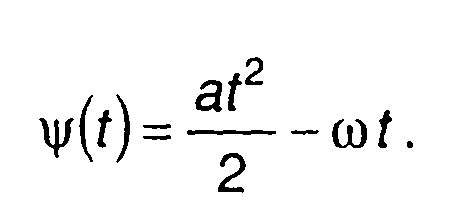(11.60)

Точку стационарной фазы получим из уравнения

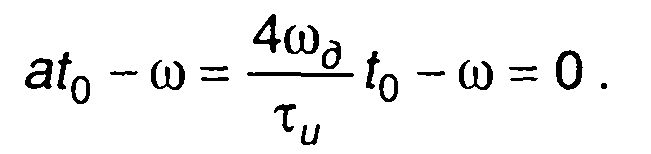(11.61)

Она равна

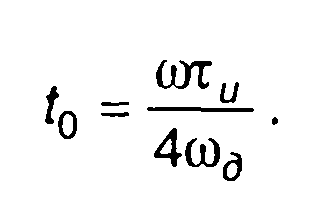(11.62)

В этом случае

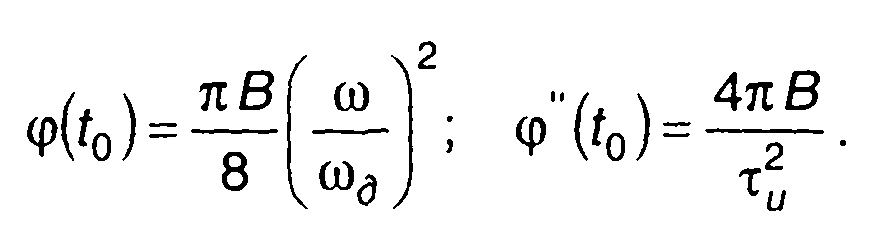(11.63)

Выражение для спектральной плотности U₁(ω) получим с уче­том (11.28) и (11.63) в виде

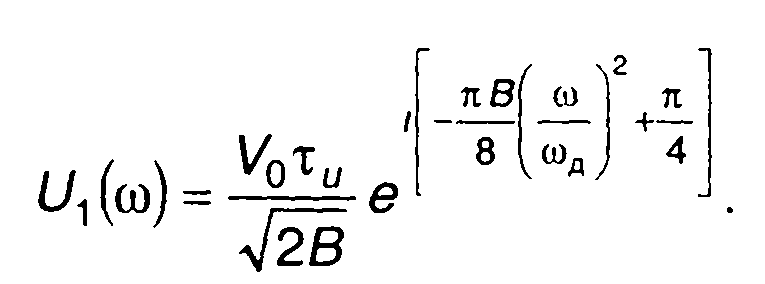(11.64)

Спектральная плотность комплексной огибающей ЛЧМ сигнала при четносимметричном законе модуляции будет описываться вы­ражением

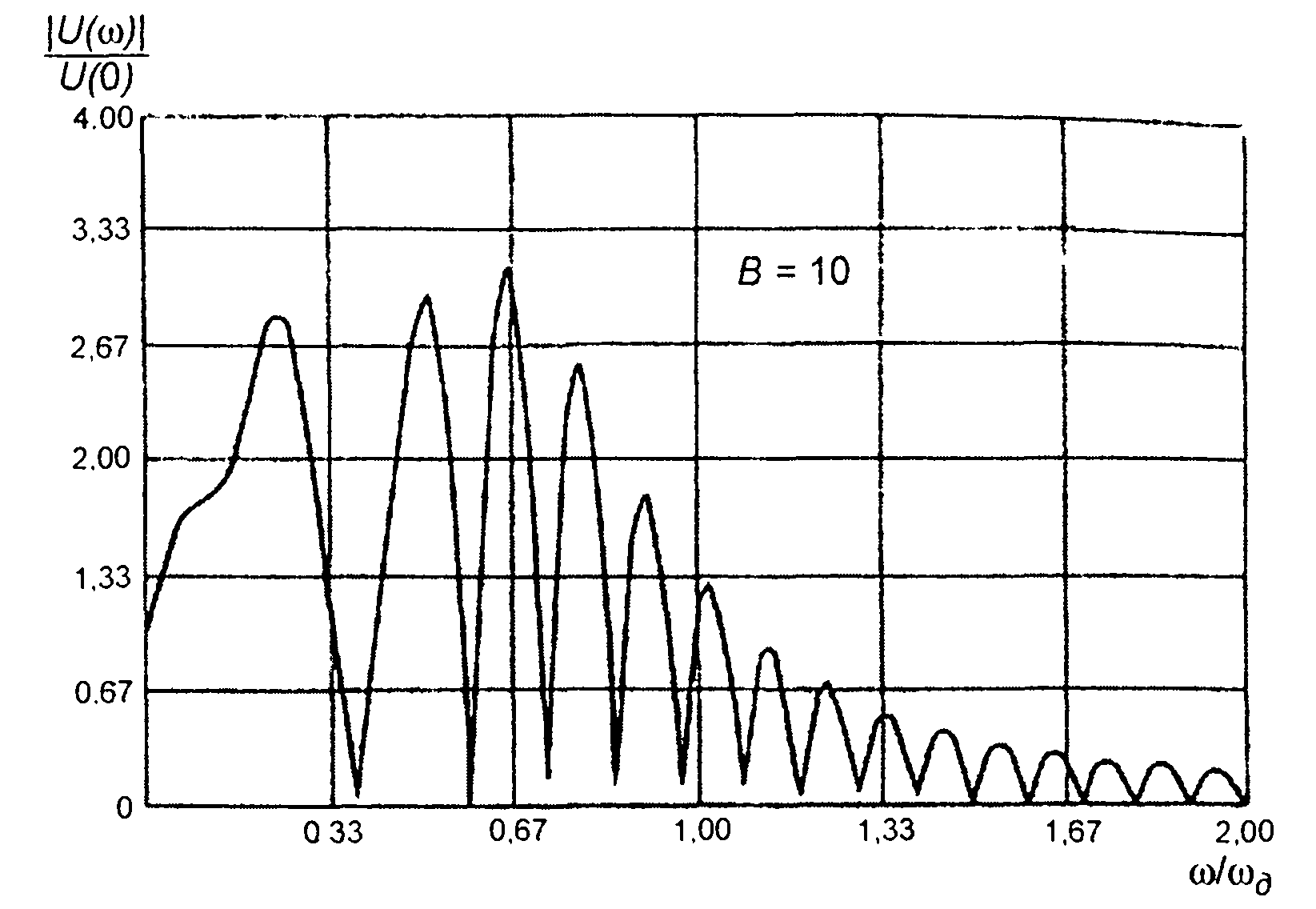
Рис. 11.7

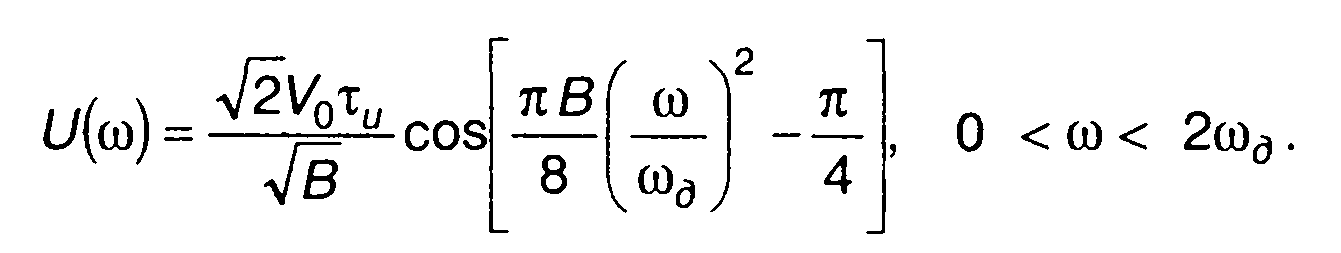(11.65)

Имея спектральную плотность одиночного импульса с четно­симметричной ЛЧМ, можно получить спектральную плотность пач­ки идентичных импульсов, используя подход, описанный в п.11.3, умножая (11.55) на (11.41).

Корреляционную функцию комплексной огибающей определим, исходя из (11.48). Расчеты показывают, что вторым слагаемым в

(11.48) можно пренебречь. Это объясняется тем, что под знаком интеграла - синус с малым значением аргумента. Выражение для корреляционной функции будет аналогичным (11.50).

11.7. Влияние искажений закона модуляции на характеристики сигнала

При формировании ЛЧМ сигнала возможны искажения закона модуляции, которые, как правило, носят колебательный характер. При нечетносимметричном законе ЧМ такие искажения могут быть учтены при описании ω(t) следующим выражением (рис. 11.10):

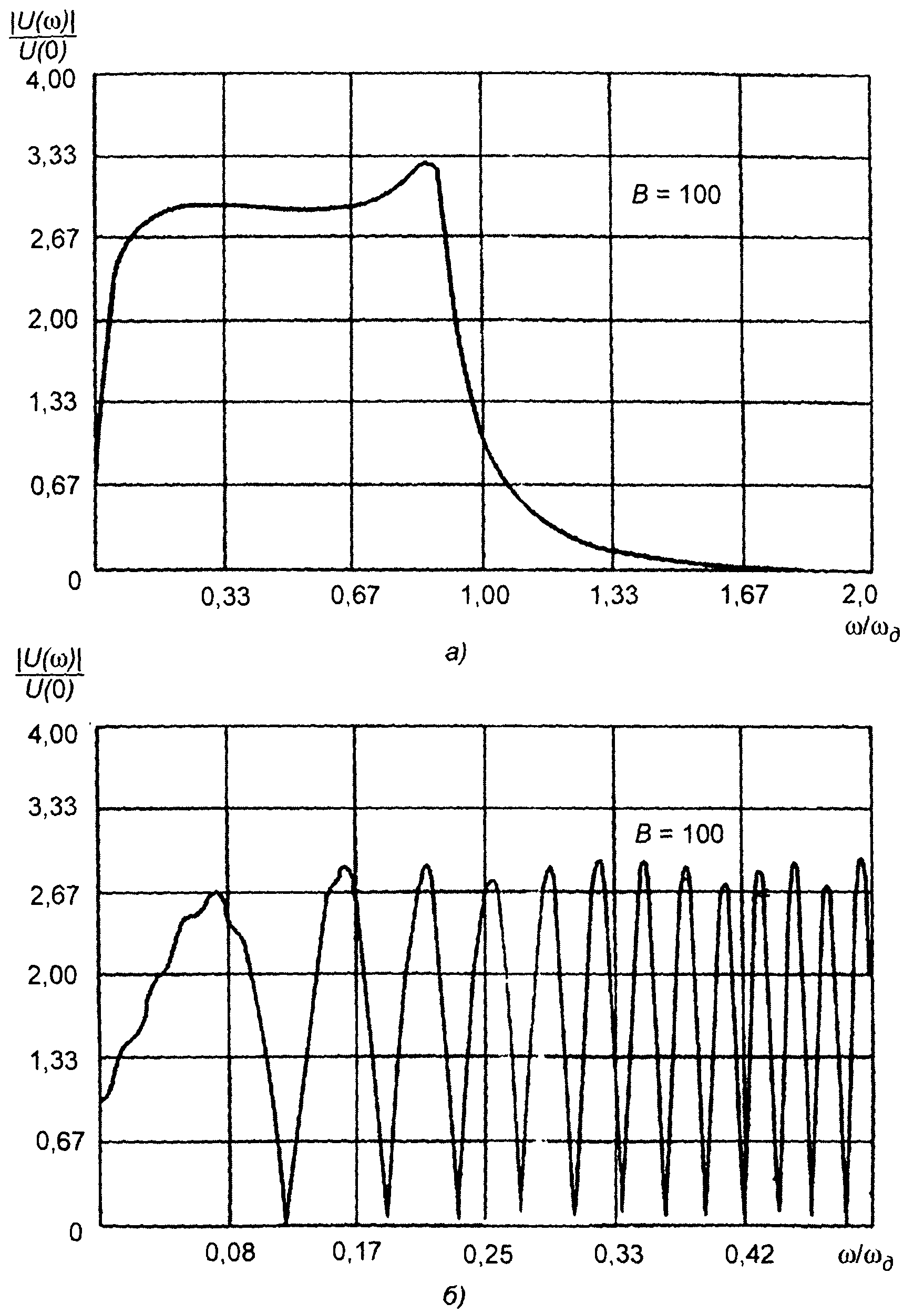
Рис. 11.8

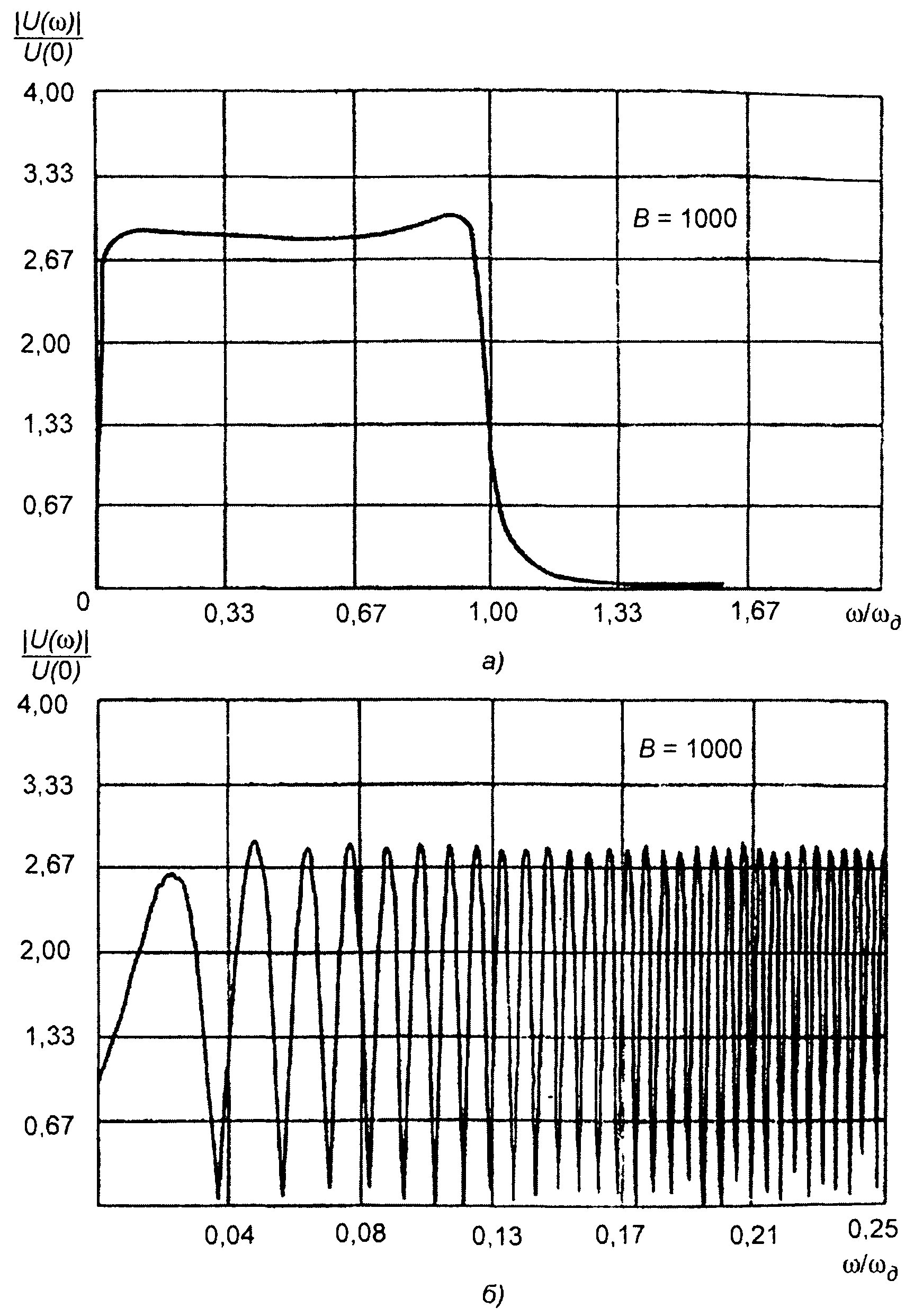
Рис. 11.9

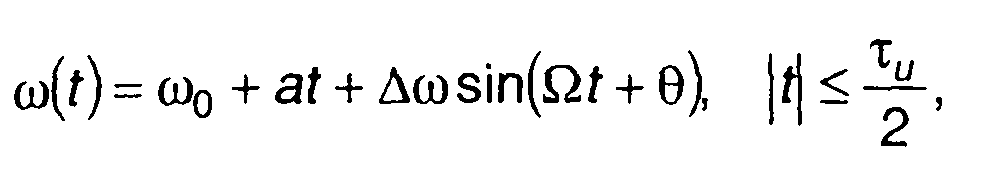(11.66)

2(i)

где a = (2ω_д) /τ- девиация частоты; ∆ω, Θ - параметры зависи- т

мости; Ω - частота искажений.

Обозначим Ω₁=2π/τ_u и примем Ω = pΩ₁ р = 1,2,... Фаза сиг­нала φ(t) с учетом (11.66) равна

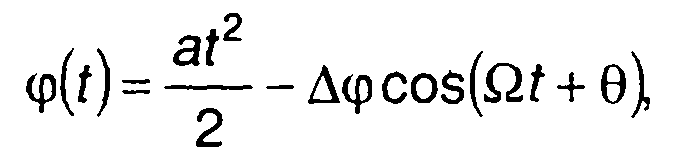(11-67)

где ∆φ = ∆ω/Ω.

Спектральная плотность комплексной огибающей сигнала опи­сывается выражением

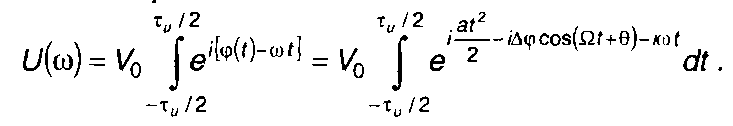(11.68)

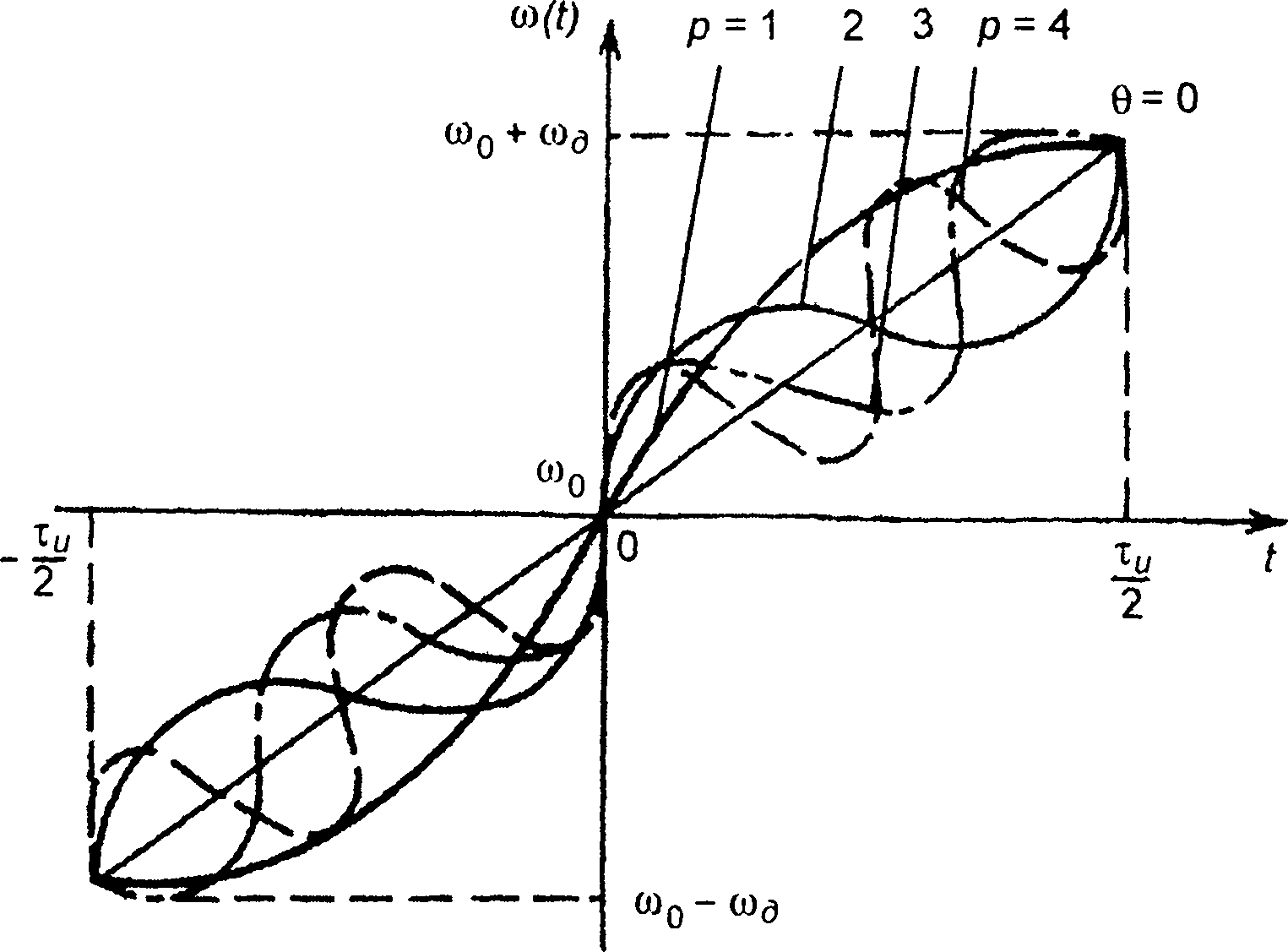
Рис. 11.10

Используя известное разложение

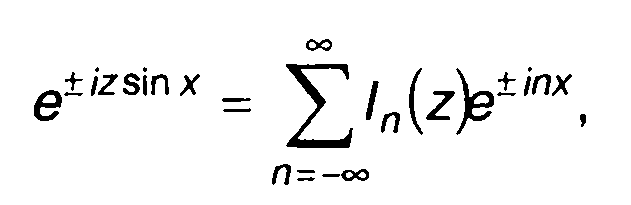(11.69)

где l_n(z) - функция Бесселя первого рода n-го порядка, выражение (11.68) представим в виде

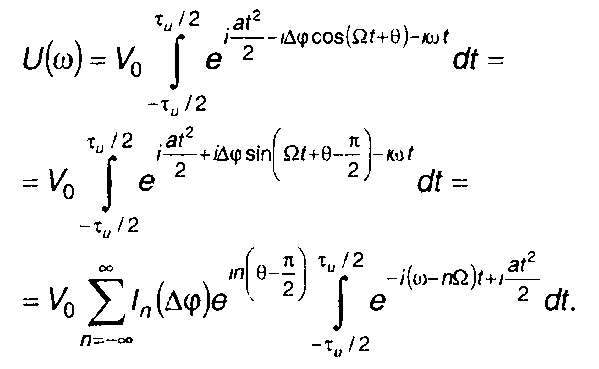(11.70)

Вводя интегралы Френеля C(z) и S(z), получим

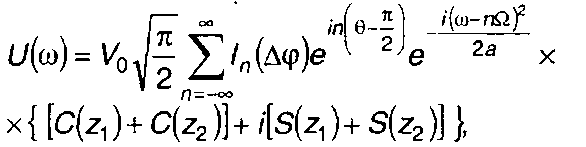
где

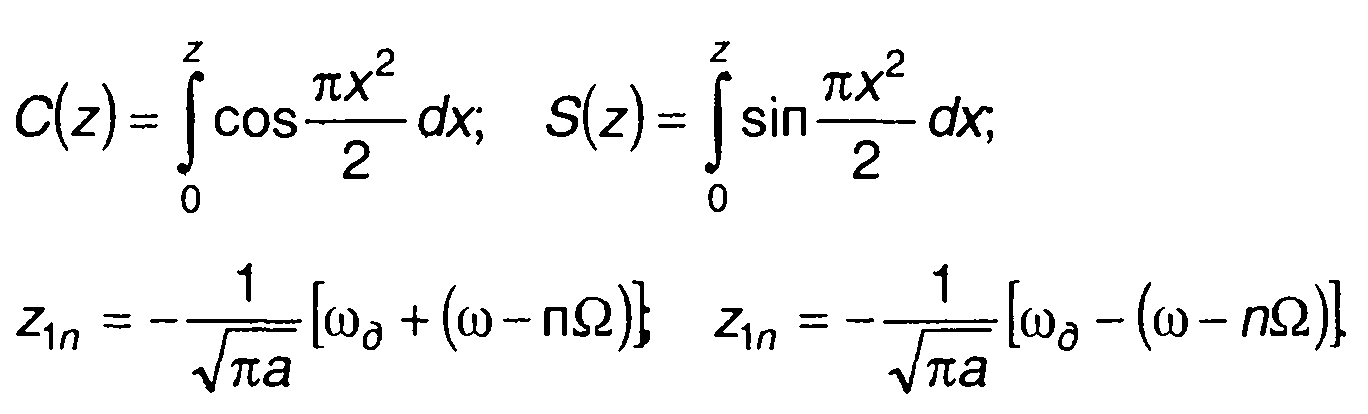(11.71)

При отсутствии искажений закона модуляции (∆ω = 0) выраже­ние (11.71) описывает спектральную плотность комплексной оги­бающей ЛЧМ сигнала, совпадает с ранее приведенным выраже­нием.

При малых искажениях (малое значение ∆ω) можно принять

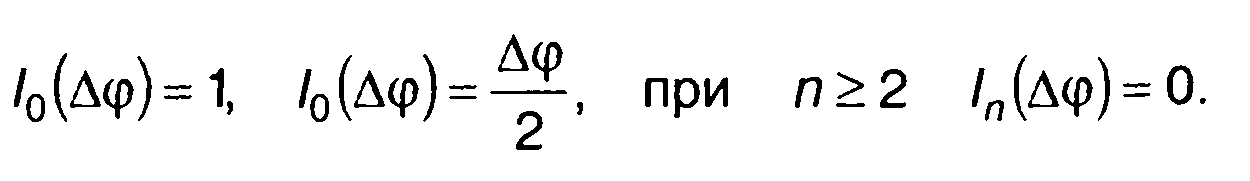
В этом случае (11.71) примет вид

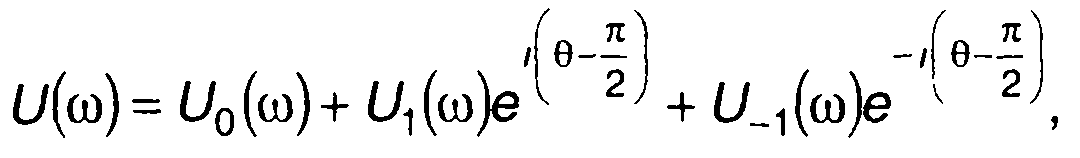(11.72)

где U₀(ω), U₁(ω) и U_₁(ω) определяются из выражения

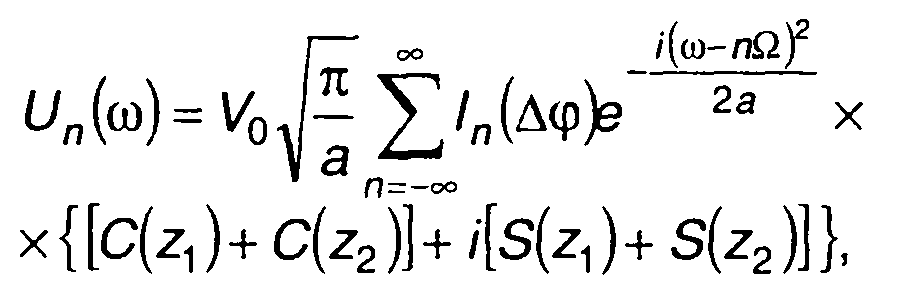(11.73)

при n = О, n = 1 и n = —1.

Графики модуля спектральной плотности комплексной огибаю­щей ЛЧМ сигнала с искажениями закона модуляции приведены на рис. 11.11. Сравнение приведенных графиков и графиков, полу­ченных для ЛЧМ сигнала без искажения закона модуляции (рис. 11.4), показывает появление при искажении закона дополнитель­ных пульсаций амплитудного спектра. Амплитуда и частота пуль­саций зависят от параметров, характеризующих искажение закона модуляции ∆ω и Ω