ДЕТЕРМИНИРОВАННЫЕ СИГНАЛЫ 7 страница

где Т - интервал дискретизации, Т ≤π/ω_m ; ω_m - максимальная час­тота в спектре сигнала;

Записанное выражение может рассматриваться как разложение непрерывного сигнала в ряд по ортогональной системе функций (рис.6.10)

(6.65)

с коэффициентами, равными значениям сигнала в выбранные мо­менты времени.

Если сигнал определен на интервале [О, Т_c], то число интерва­лов разбиения равно

(6.66)

а ряд Котельникова примет вид

(6.67)

Ряд Котельникова может быть записан и для частотной области

(6.68)

где S(ω) - спектральная плотность сигнала s(t); Ω = 2π/T_c - интер­вал дискретизации по частоте.

Общее число выборочных значений определяется как

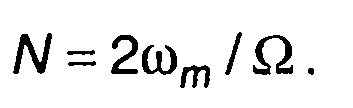(6.69)

Примеры восстановления спектров сигналов по их дискретным значениям с использованием ряда Котельникова приведены в кон­це разд. 7.

Взяв выборочные значения сигнала, можно произвести его сту­пенчатую аппроксимацию

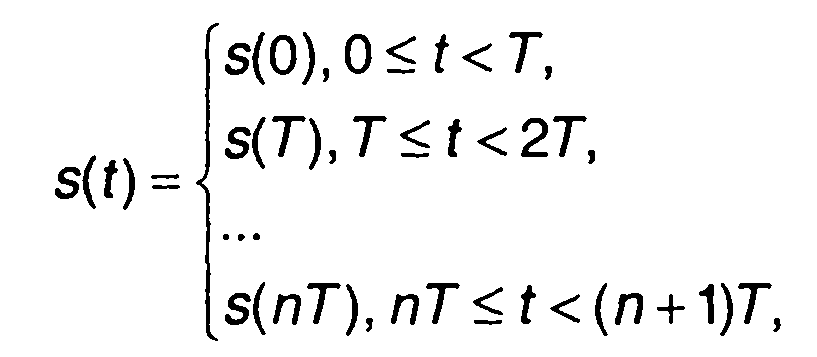(6.70)

где Т- интервал дискретизации сигнала по времени.

Выражение для спектральной плотности сигнала запишем в виде

Рис. 6.10

(6.71)

Из (6.71) с уметом (6.70) получим

(6.72)

Для четной функции s(t) запишем

(6.73)

Аналогично можно подучить выражение, связывающее сигнал с выборочными значениями спектральной плотности

(6.74)

Для действительной функции S(nΩ) получим

(6.75)

Выражения (6.72) - (6.75) аналогичны ряду Котельникова. Они позволяют восстановить сигнал по дискретным значениям спектра и спектр по дискретным значениям сигнала.

Раздел 7.

ВОССТАНОВЛЕНИЕ НЕПРЕРЫВНЫХ СИГНАЛОВ С ПОМОЩЬЮ СПЛАЙНОВ

Одним из видов интерполирующей функции является сплайно- вая функция, или сплайн. Сплайн описывает интерполируемую функцию на каждом частном интервале дискретизации. Так, если функция задана на интервале [t₀, t_N], который выборкой разбит на частные интервалы [t_k> t_k+1], то сплайны дают описание функции на каждом частном интервале [t_k, t_k+1], а их совокупность описывает функцию на всем интервале ее задания (рис. 7.1). Обычно сплайн представляет степенной многочлен. Такого вида сплайны и рас­сматриваются в дальнейшем.

Интерполирующая функция φ_k(t) называется сплайном степени

n дефекта v, если она удовлетворяет следующим условиям:

на каждом интервале [t_k, t_k+1] функция является многочленом степени n;

(7.1)

непрерывна и имеет на концах интервала (n - v) непрерывных про­изводных, т.е.

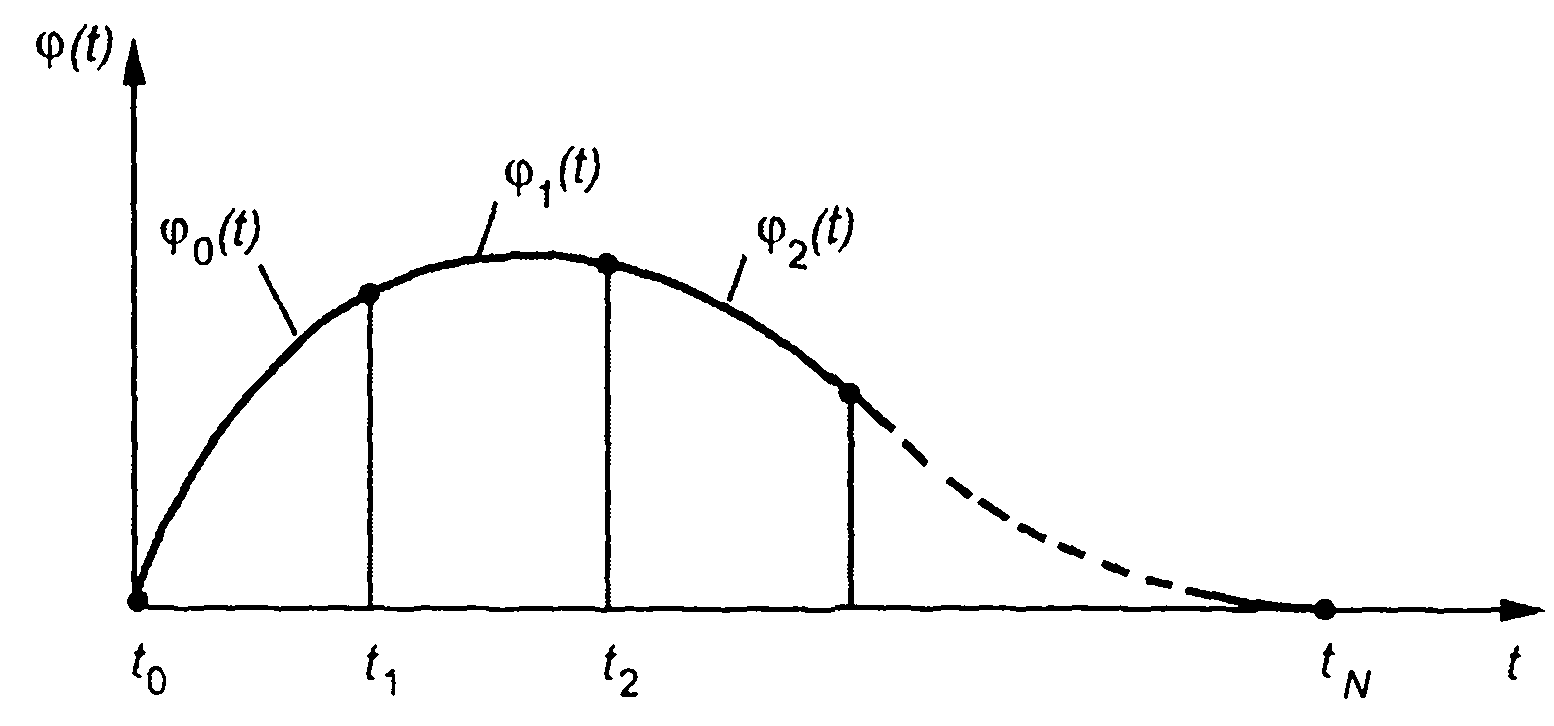
Рис. 7.1

Говорят, сплайн обладает n-v степенью гладкости.

Предельный вариант сплайна - кусочно-линейная функция, применяемая при линейной интерполяции. Такую функцию можно рассматривать как сплайн первой степени (n = 1) дефекта 1 (v = 1) Простейшими сплайнами, пригодными для использования на практике, являются кубические сплайны третьей степени де­фекта 2 или 1. На их примере рассмотрим общий подход к по­строению сплайнов.

В дальнейшем излагаются методы построения сплайнов более сложной структуры, приводятся выражения для различных видов сплайнов, даются примеры их применения при восстановлении не­прерывных сигналов - интерполяции временной функции, описы­вающей сигнал.

Одним из достоинств сплайновой интерполяции является то, что не требуется равномерной сетки интерполяции функции. В то же время на практике чаще всего используется постоянный интер­вал дискретизации сигнала. Вследствие этого в дальнейшем рас­сматривается вариант с равномерной сеткой интерполяции. Сплай­ны, построенные на равномерной сетке интерполяции, называются стационарными. Целесообразность такого рассмотрения подкреп­ляется еще и тем, что в этом случае выражения, описывающие сплайны, и приводимые в качестве иллюстрации методы, получа­ются проще.

7.1. Кубические сплайны первой степени гладкости

Сплайны третьей степени дефекта 2 называются кубическими сплайнами первой степени гладкости или эрмитовыми кубическими сплайнами. Исходными данными для их получения являются зна­чения сигнала s(t_K) и его первых производных в узлах интерполяции (ds/dt)_tk. На каждом частном интервале [t_K, t_K+1] сплайн описывается выражением

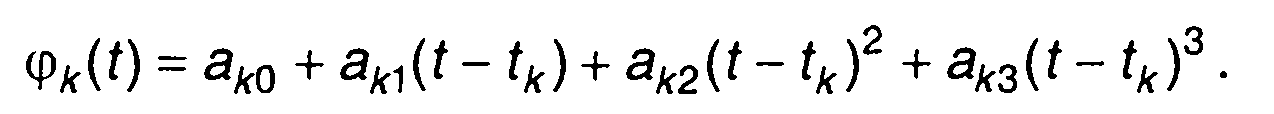(7.2)

В точках дискретизации сплайн и его первая производная равны значениям сигнала и его производной

(7.3)

Из (7.2) и (7.3) для начала и конца каждого частного интервала [t_K, t_K+1] получим четыре уравнения, которые позволяют определить четыре коэффициента (а_ко, а_К1, а_К2, а_кз), задающие сплайн. С уче­том значений этих коэффициентов выражение для сплайна (7.2) примет вид

(7.4)

где

Если функция задана только своими значениями (наиболее рас­пространенный на практике случай), для задания значений на кон­цах частного интервала [t_K, t_K+1] можно использовать следующее выражение:

(7.5)

На границах интервала задания функции:

(7.6)

В практике интерполяции сигналов и их характеристик наиболее удобной формой представления интерполирующей функции явля­ется следующая (разд. 6)

(7.7)

где s_k = s(t_K) - дискретные значения сигнала (значения интерполи­руемой функции в узлах интерполяции).

Приводя выражения для сплайнов к виду (7.7), для случая t_k+1 - t_k= h, S_o= S_n= 0 получим:

на первом интервале

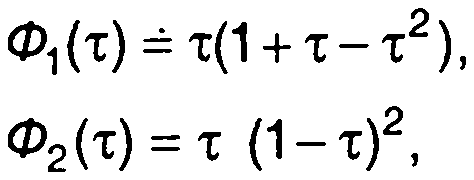(7.8)

где τ = t-t_k/h,

на k-м интервале [t_k, t_k+1]

(7.9)

на последнем интервале

(7.10)

7.2. Кубические сплайны второй степени гладкости

Большую гладкость интерполяции обеспечивает кубический сплайн второй степени гладкости (дефекта 1). Он представляет многочлен третьей степени (7.2), его значения в узлах интерполя­ции равны значениям сигнала

(7.11)

имеет в узлах интерполяции непрерывные первые две производ­ные

(7.12)

При описании сплайна на частном интервале [t_k, t_k+1] использует­ся его запись в виде (7.7).

Чтобы выполнить условие (7.12), продифференцируем дважды (7.4) и для t_k- левой границы интервала [t_k, t_k+1] (τ = 0) получим

(7.13)

Аналогично для правой границы интервала [t_k-h t_k) (τ = 1) найдем

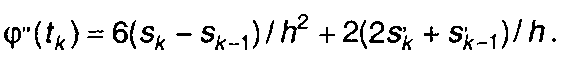(7.14)

Приравнивая (7.13) и (7.14), получаем

(7.15)

Такие уравнения могут быть получены для узлов интерполяции при к = 2,..., N - 1. Полученная система уравнений должна быть до­полнена соотношениями для производных на границах общего ин­тервала [t₀, t_N], позволит однозначно определить все производные s’_k. Таким образом, сплайн на каждом частном интервале опреде­ляется всей совокупностью значений s_k и краевыми условиями. В этом смысле такой сплайн называется глобальным. Он требует большого объема вычислений, особенно при большом значении N.

Рассмотренные кубические сплайны дефекта 1 обладают дос­таточно хорошими интерполяционными свойствами. Однако син­тез таких функций связан с определенными трудностями и для них характерен большой объем вычислений. Поэтому при интер­поляции функций (восстановлении непрерывных сигналов по их дискретным значениям) более удобными могут оказаться локаль­ные сплайны.

7.3. Подход к построению локальных сплайнов

Одним из достоинств сплайновой интерполяции является воз­можность решения задачи при неравномерной сетке интерполяции. Однако более простыми являются стационарные сплайны - сплай­ны, формируемые на равномерной сетке. На их примере и рас­смотрим принцип построения локальных сплайнов.

Для построения локальных сплайнов могут использоваться раз­личные подходы. В настоящем разделе дается достаточно простой, изложенный в [38]. Ограничимся рассмотрением случая, когда сплайны представляют степенные многочлены.

Рассмотрим функцию s(t), заданную своими значениями s(t_k) = s_к в точках дискретизации {t_k},k = 0,1,2,...,N, на интервале [t₀, t_N]. Вы­делим интервал [Т₁ Т₂], границы которого: T1e[tk_₁,t_k] и T₂e[t_k,t_k+1] (рис. 7.2). В окрестности точки T₁ возьмем симмет­рично (N₁+1) точек дискретизации t_k-1 t_k, t_k-2, t_k+₁..., построим много­член L₁(t), проходящий через соответствующие значения функции s_k.₁, s_k, s_k_₂, s_k+1,... и содержащий (N₁+1) членов.

Аналогично построим многочлен L₂(t) на точках, выбранных симметрично Т₂, проходящий через значения функции s_k, s_k+1 s_k-1 s_k+2,... содержащий (N₂+1) членов.

На интервале [Т₁, Т₂] построим многочлен φ_k(t), содержащий N₁+N₂+3 членов.

Коэффициенты многочлена найдем из условий:

многочлен проходит через точки L₁(T₁), s_k ,.L₂ (Т₂);

Рис. 7.2

производные многочлена на границах интервала совпадают с производным и L₁(t) и L₂(t):

(7.16)

Уравнения, составленные исходя из условий (7.16), позволяют определить коэффициенты многочленаφ_k(t). Преобразовав его к виду (7.7), получим сплайн, описывающий функцию на интервале [Т₁, Т₂], имеющий требуемый вид.

Аналогично выделим интервал, примыкающий слева к [Т₁, Т₂] и на нем построим многочлен φ_k_₁(t) так же, как строился φ_k(t). За­тем на интервале, примыкающем справа к [Т₁, T₂], построим много­член φ_k+1(t). Таким образом, получим совокупность многочленов на всем интервале задания функции, многочлены проходят через за­данные точки, имеют определенное число производных на грани­цах выделяемых интервалов. На первом интервале [to, Т₁] и по­следнем [T₂, t_N] интерполирующая функция совпадает с многочле­нами L₁(t) и L₂(t) соответственно.

Используя изложенный подход к синтезу локальных сплайнов и обеспечивая заданное число непрерывных производных, можно получить различные виды сплайнов, описывающих заданную функцию.

7.4. Локальные сплайны нечетной степени гладкости

Ниже рассматривается метод синтеза локальных стационарных сплайнов, имеющих нечетное число непрерывных производных. Синтез сплайнов производится с использованием общего подхода, описанного в п. 7.3.

7.4.1. Локальные сплайны первой степени гладкости

Кусочно-линейная интерполяция не имеет большого практиче­ского значения. Чаще используются сплайны более высокого по­рядка. Однако на ее примере проще рассмотреть подход и основ­ные особенности интерполяции на основе локальных сплайнов.

Функция, описывающая сигнал, задана дискретными значениями на интервале [t₀, t_N] с равномерной сеткой и постоянным шагом h (рис. 7.2).

Выделим интервал [Т₁ Т₂], где T₁ = 0,5(t_k + t_k) и T₂ = 0,5(t_k + t_k+1).

Определим значения функций L₁(t) и L₂(t) и их первых производных на границах интервала [Т₁, Т₂] с использованием линейной интер­поляции

(7.17)

На интервале [Т₁, Т₂], построим степенной многочлен четвертой степени

(7.18)

так, как это описано в п.7.3: на границах интервала значения много­члена и его первых производных совпадают со значениями, опре­деляемыми (7.17), а в точке t_k - значением s_k

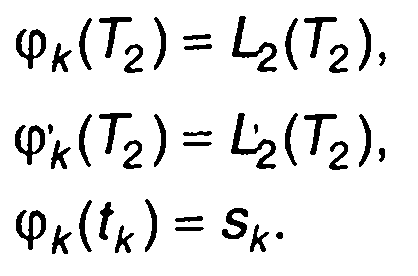(7.19)

Из (7.17) - (7.19) получим выражения для коэффициентов мно­гочлена (7.18)

(7.20)

Таким же образом можно построить многочлены φ_k(t) на всех

частных интервалах. На первом интервале и последнем функция восстанавливается линейно.

Преобразуя полученную совокупность многочленов {φ(t)} к виду

для базисных функций Ф_k(t) получим следующие выражения.

На первом интервале:

(7.21)

На k-м интервале [t_k-0,5h,t_k +0,5h], k = 2,...,N-1, N≥3:

(7.22)

На последнем интервале:

(7.23)

Графики базисных функций приведены на рис. 7.3 - 7.5 (в конце раздела). Примеры восстановления непрерывных сигналов по их дискретным значениям с помощью степенных локальных сплайнов приведены на рис. 7.6 - 7.8 (интервал дискретизации - единица).

Сплайны с одной непрерывной производной являются наиболее простыми. Качество интерполяции функций с их использованием такое же, как и при использовании эрмитовых сплайнов. Оно может оказаться достаточным при интерполяции относительно простых зависимостей.

7.4.2. Локальные сплайны третьей степени гладкости

Используя общий подход, проведем построение локальных сплайнов третьей степени гладкости. Для этого выделим интервал [Т₁ ,Т₂], с границами на серединах смежных частных интервалов разбиения (рис. 7.2):

Через точки s_k-2,...,s_k+1 проведем многочлен L₁(t) третьей степе­ни. Выражение для него будет иметь вид:

(7.24)

где τ = 1 / h( t - t_k_₁).

Для левой границы интервала [Т₁, Т₂], получим:

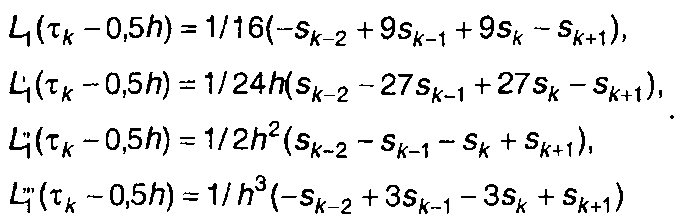(7.25)

Через точки s_k-1,...,s_k+2 проведем многочлен L₂(t) третьей степени (аналогично многочлену L₁(t). Так же, как для L₁(t), получим зави­симости для значения L₂(t) и трех его производных на правой границе

интервала [T₁, Т₂], в точке t_k+ 0,5h. Эти значения описываются (7.25) при увеличении индекса s на единицу.

В соответствии с общим подходом, изложенным в п.7.3, на интер­вале [T₁,Т₂], строится многочлен 8-й степени φ_k(t), N₁=N₂ = 3. Так же строятся многочлены на всех остальных интервалах. На первом и последнем интервалах для интерполяции используются многочлены L₁(t) и L₂(t), проведенные через первые и последние четыре точки соответственно. Полученная таким образом совокупность степенных сплайнов осуществляет интерполяцию функции на всем заданном интервале, плавно соединяя исходные дискретные значения. Преоб­разуя полученную совокупность многочленов к виду (7.7), получим следующие выражения для базисных функций Ф_k(t).

На первом интервале:

(7.26)

На k-ом интервале [t_k-0,5h, t_k+0,5h], k = 3,...,N-2, N≥ 5:

(7.27)

На последнем интервале базисные функции определяются

(7.26) с учетом следующих соотношений:

(7.28)

Рассматриваемые сплайны могут быть получены только при N ≥ 4.

Графики базисных функций при некоторых значениях N изобра­жены на рис. 7.3 - 7.5. Примеры восстановления непрерывных сиг­налов по их дискретным значениям с помощью степенных локаль­ных сплайнов приведены на рис. 7.6 - 7.8.

7.5. Локальные сплайны четной степени гладкости

На основе общего подхода (п. 7.3) получим расчетные выраже­ния для стационарных многочленных моделей, имеющих четное число непрерывных производных. Это наиболее простые локально- сплайновые модели.

7.5.1. Локальные сплайны второй степени гладкости

Функция, описывающая сигнал (или его характеристику), задана дискретными значениями на интервале [t₀, t_N] с постоянным шагом (рис. 7.2). Выделим частный интервал [t_k, t_k-1 ]и определим значения первых двух производных на границах выделенного интервала. Для этого проведем через точки s_k-1,s_k и s_k+1 степенной многочлен вто­рой степени

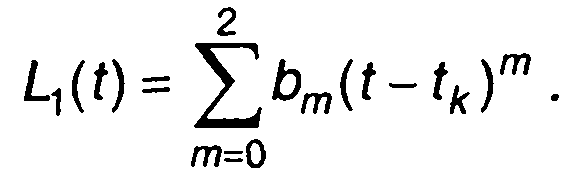(7.29)

Коэффициенты многочлена определяются из следующей систе­мы функций:

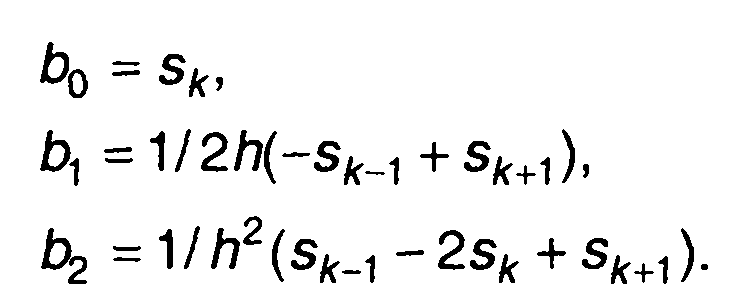(7.30)

Из (7.29) с учетом (7.30) найдем производные на левой границе выделенного интервала:

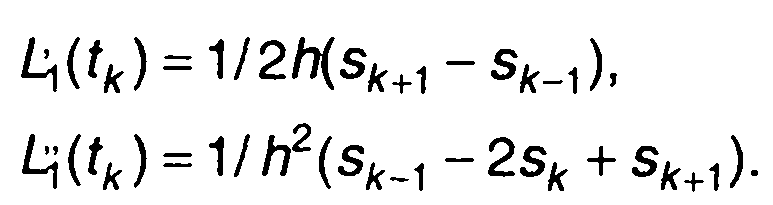(7.31)

Аналогично построим степенной многочлен второй степени L₂(t), проходящий через точки s_k, s_k+1, s_k+2. Производные L₂(t) на правой границе выделенного интервала найдутся так же, как (7.31): .

(7.32)

Построим на интервале [t_k, t_k+1] степенной многочлен φ_k(t) пятой степени

(7.33)

где τ = 1/h((t-t_k), t ϵ [t_k,t_k+1], удовлетворяющий граничным условиям

(7.34)

С учетом (7.34), (7.31) и (7.32) получим следующие выражения для коэффициентов многочлена (7.33):

(7.35)

Аналогично получим всю совокупность многочленов {φ_k(t)}. На первом частном интервале и последнем функция описывается мно­гочленами L₁(t) и L₂(t), проведенными через первые три и последние три точки. Преобразуя полученную совокупность многочленов к виду (7.7), получим следующие зависимости дли базисных функций Ф_k(t).

На первом интервале:

(7.36)

На k-м интервале [t_k,t_k+1], k = 2,...,N-2, N≥ 4:

(7.37)

На последнем интервале:

(7.38)

Графики базисных функций при некоторых значениях N изобра­жены на рис.7.3 - 7.5. Примеры восстановления непрерывных сиг­налов по их дискретным значениям с помощью степенных локаль­ных сплайнов приведены на рис. 7.6 - 7.8.

7.5.2. Локальные сплайны четвертой степени гладкости

При переходе к сплайнам, имеющим непрерывными четыре первые производные, качество интерполяции (гладкость) улучша­ется. Принцип их построения описан в п. 7.3. Операции построения сплайна аналогичны описанным в п. 7.5.1.

Выделим интервал [t_k, t_k+1] (рис. 7.2), и на левой границе интер­вала через пять точек s_k.₂, s_k-1,.., s_k+2 степенной многочлен

(7.39)

Приравнивая значения функции и многочлена (7.39) в выбран­ных точках, получаем следующие выражения для коэффициентов:

(7.40)

Дифференцирование (7.39) с учетом (7.40) дает выражения для первых четырех производных на левой границе рассматриваемого интервала в виде:

(7.41)

Аналогично задается степенной многочлен L2(t) на правой границе выделенного интервала, который проходит через точки s_k-1,..,s_k+3 . Для него получим:

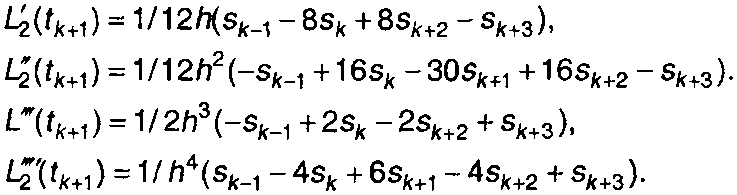(7.42)

На интервале [t_k, t_k+1] строим степенной многочлен девятой степени

(7.43)

где т = 1/h(t-t_k).

Многочлен проходит через точки s_k и s_k+1, на границах интервала имеет производные, равные (7.41) и (7.42). Из этих условий опре­деляются коэффициенты в (7.43):

(7.44)

Аналогично строятся многочлены φ_k(t) на всех частных интер­валах [t_k, t_k+1]при k = 3,...,N-2. На первом и последнем интервалах интерполируемая функция описывается многочленами L₁(t), проходящим

через первые пять ее значений, и L₂(t), проходящим через последние пять значений функции.

Преобразуя полученные многочлены к виду (7.7), получаем сле­дующие выражения для базисных функций.

На первом интервале:

(7.45)

На k-м интервале [t_k,t_k+1], k = 3,...,N-2, N≥ 6:

(7.46)

На последнем интервале базисные функции симметричны функ­циям на первом интервале, вычисляются по (7.45) с учетом сле­дующих соотношений:

(7.47)

Рассматриваемые сплайны могут быть получены только при N > 5.

Графики базисных функций при некоторых значениях N изобра­жены на рис. 7.3 - 7.5. Примеры восстановления непрерывных сиг­налов по их дискретным значениям с помощью степенных локаль­ных сплайнов приведены на рис. 7.6 - 7.8.

Анализ приведенных на рис. 7.6 - 7.8 интерполяционных функ­ций, построенных с использованием ряда Котельникова, многочле­нов Лагранжа и сплайновых функций, дает возможность сравнить качество интерполяции для различных видов исходных сигналов.

Рис. 7.3

Рис. 7.4

Рис. 7.5

Рис. 7.6

Рис. 7.7

Рис. 7.8

Раздел 8.

УЗКОПОЛОСНЫЕ СИГНАЛЫ

Узкополосные сигналы составляют широкий класс сигналов, ко­торые формируются и обрабатываются в различных радиотехниче­ских системах. Это прежде всего различные виды модулированных сигналов. Особенности структуры узкополосных сигналов опреде­лили возможность, а часто и необходимость, особого подхода к их описанию и анализу, а, следовательно, целесообразность их от­дельного рассмотрения.

8.1. Описание узкополосного сигнала

К узкополосным сигналам относятся сигналы, спектры которых сосредоточены в относительно узкой по сравнению со средней час­тотой полосе (рис. 8.1,а). Узкополосный сигнал описывается выра­жением

(8.1)

где V(t) , Ф(t) - амплитуда и фаза сигнала; ω₀- несущая частота.

Амплитуда V(t) и фаза φ(t) содержат передаваемую информа­цию, являются функциями времени и представляют модулируемые параметры сигнала. Это медленно меняющиеся функции времени, их изменения за период 2π/ω₀ незначительны, таким образом, вы­полняется условие узкополосности сигнала.