ДЕТЕРМИНИРОВАННЫЕ СИГНАЛЫ 5 страница

Тогда

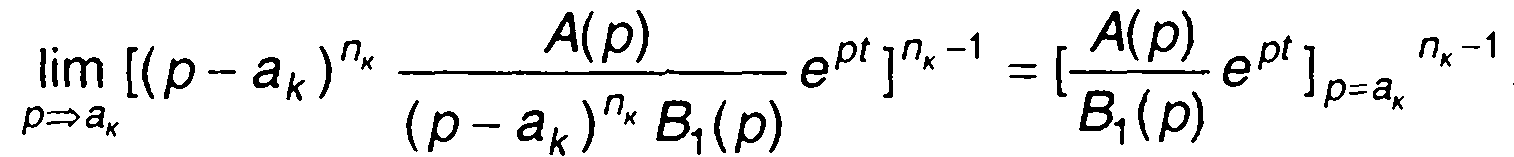.(4.17)

В том случае, когда полюсы простые, выражение (4.15) упроща­ется

(4.18)

Если корень знаменателя равен нулю, то В(р) можем представить в виде

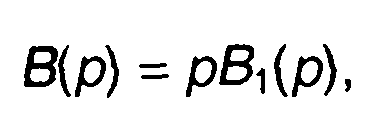(4.19)

где В₁(0)≠0.

С учетом (4.19) запишем

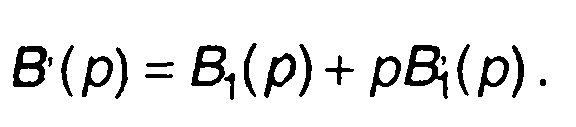(4.20)

При этом В'(0) = B'₁(0), а В'(а_к) = а_кВ'(а_к). При записи последне­го равенства учтено, что В₁(а_к) = 0, так как все ненулевые корни многочленов В(р) и В₁(р) совпадают.

Таким образом, получим

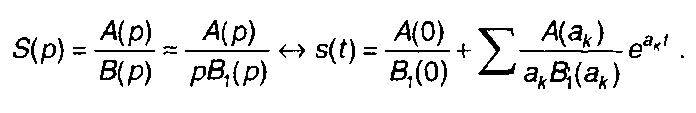(4.21)

Сумма в (4.21) берется по всем ненулевым корням многочлена В(р) или по всем корням В1(р).

В качестве примера рассмотрим изображение

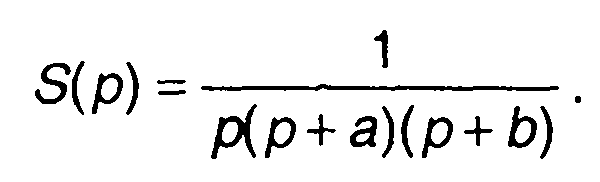
В записанном выражении имеем А(р)= 1, В(р)=р(р+а)(р+Ь), В1(р)= =(р+а)(р+Ь). Производная В¹₁(р)=(р+а)+(р+Ь). Корни знаменателя: p₁=0, p₂=-а, р₃=-Ь.

В соответствии с (4.21), получим

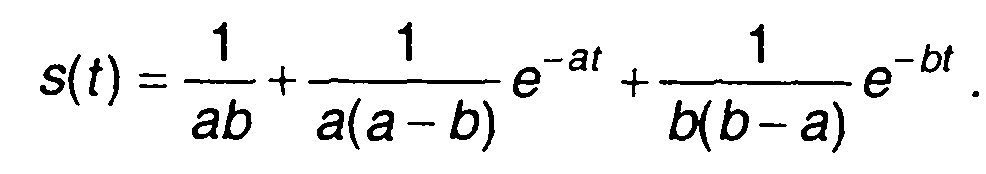
При нахождении оригинала по его изображению возможен и иной подход, который наиболее часто используется в инженерной практике. Он заключается в том, что выражение

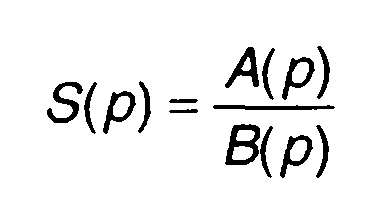
раскладывается на простые дроби. Оригинал находится с помощью известных формул однозначного соответствия оригинала и изобра­жения, сведенных в таблицу. В частности, рассмотренное выше:

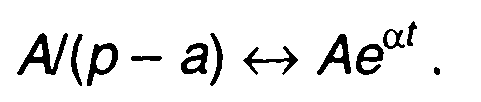
Для условий приведенного выше примера запишем

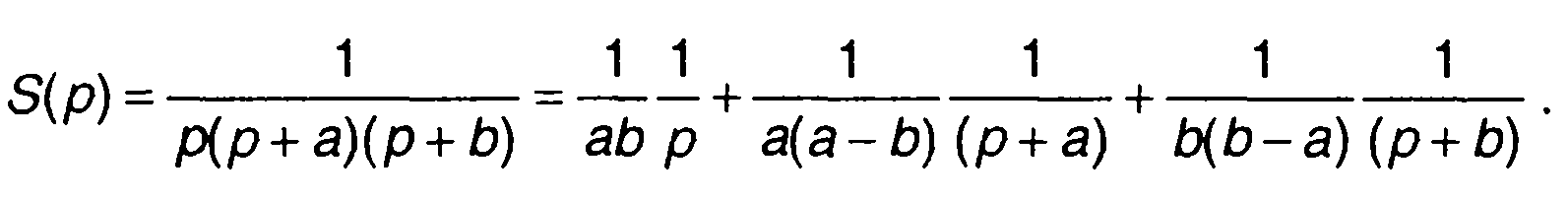
Используя формулы соответствия для слагаемых, найдем

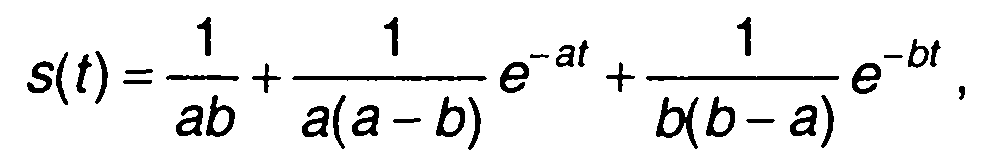
что совпадает с ранее полученным результатом.

Сигналы (оригиналы), соответствующие наиболее часто встре­чающимся преобразованиям Лапласа (изображениям) в виде дроб­но-рациональных выражений, приведены в табл. 4.3. Более полная таблица дана в [ 28 ].

Таблица 4.3.

Обратные преобразования Лапласа дробно-рациональных функций

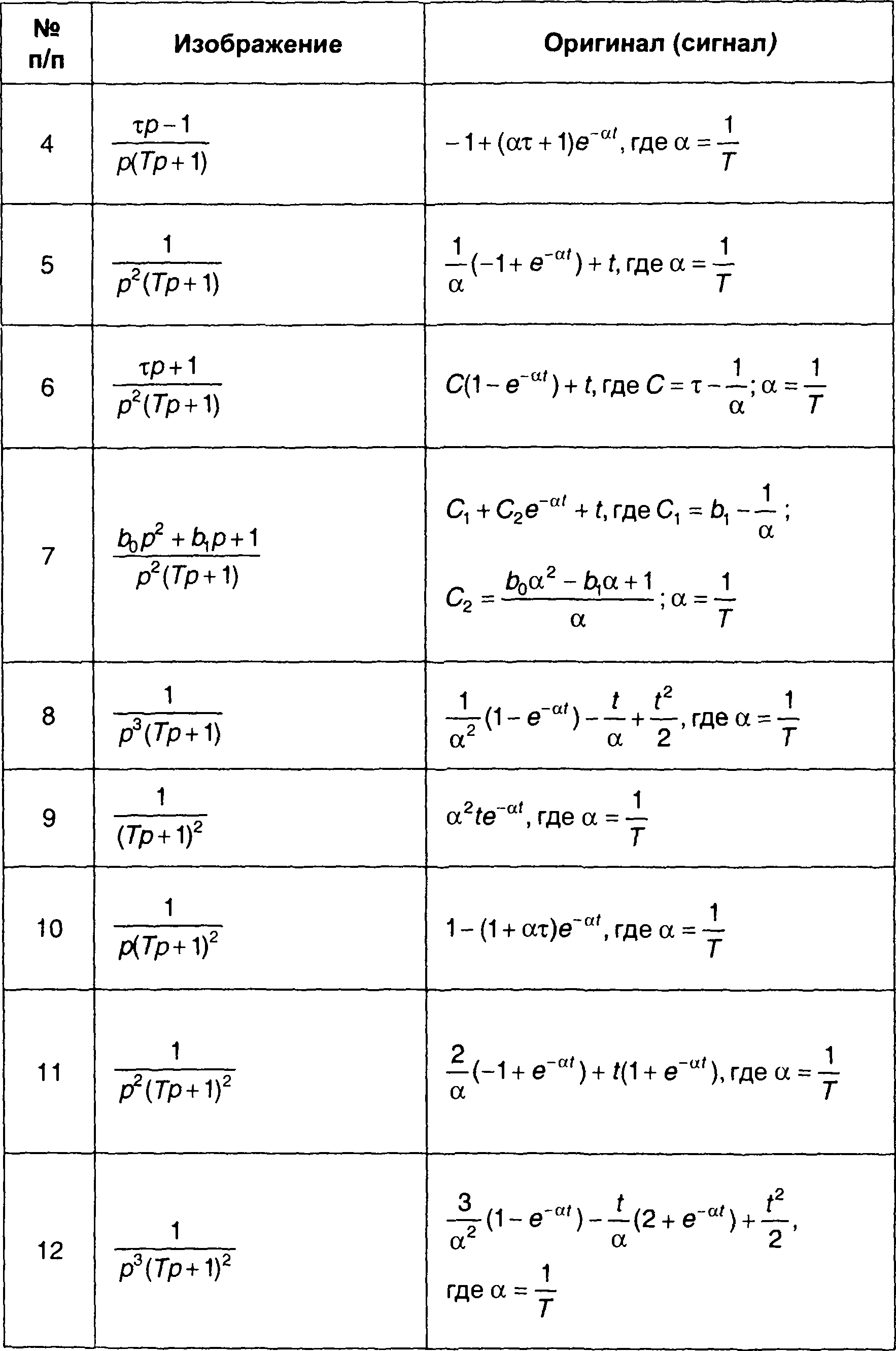
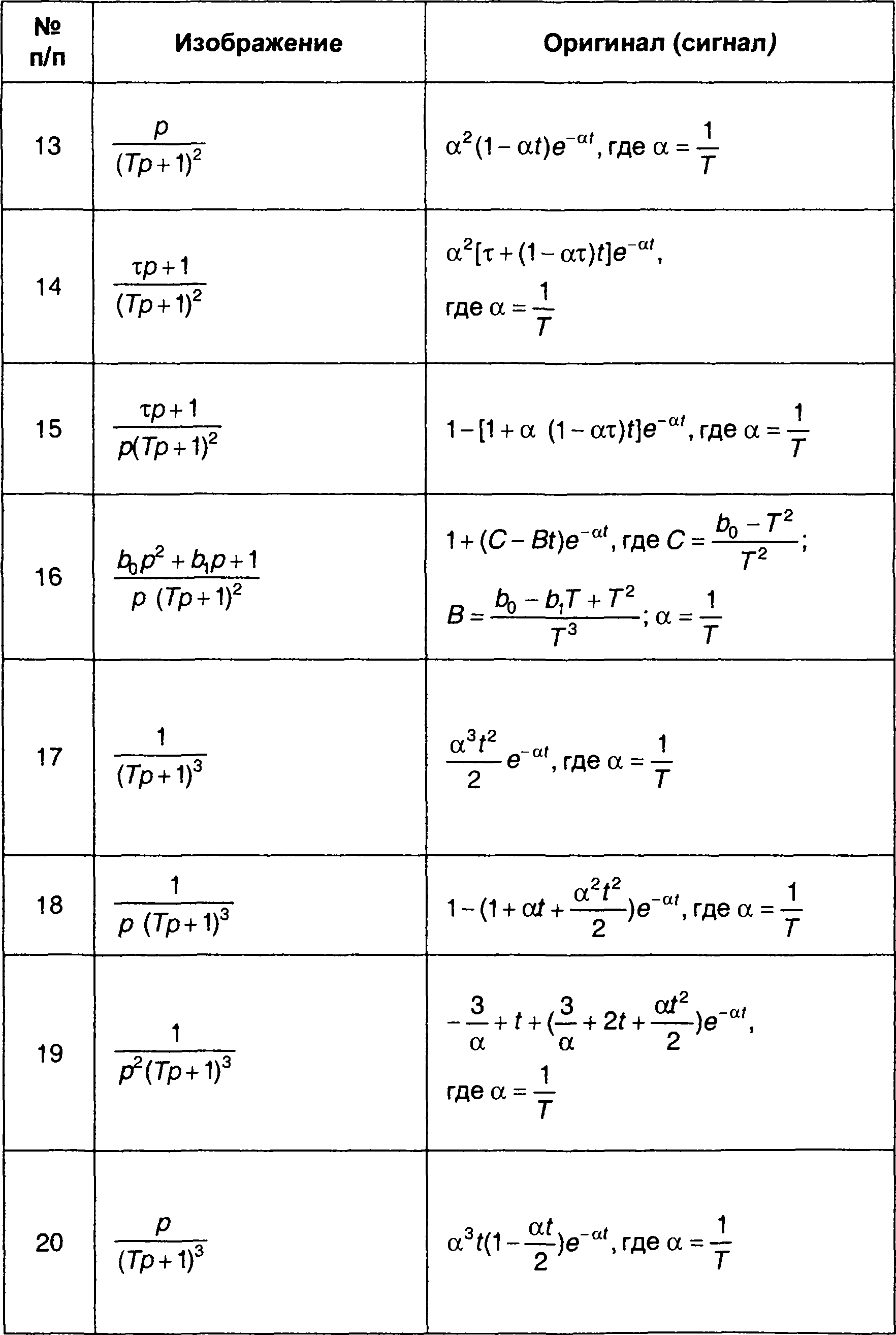
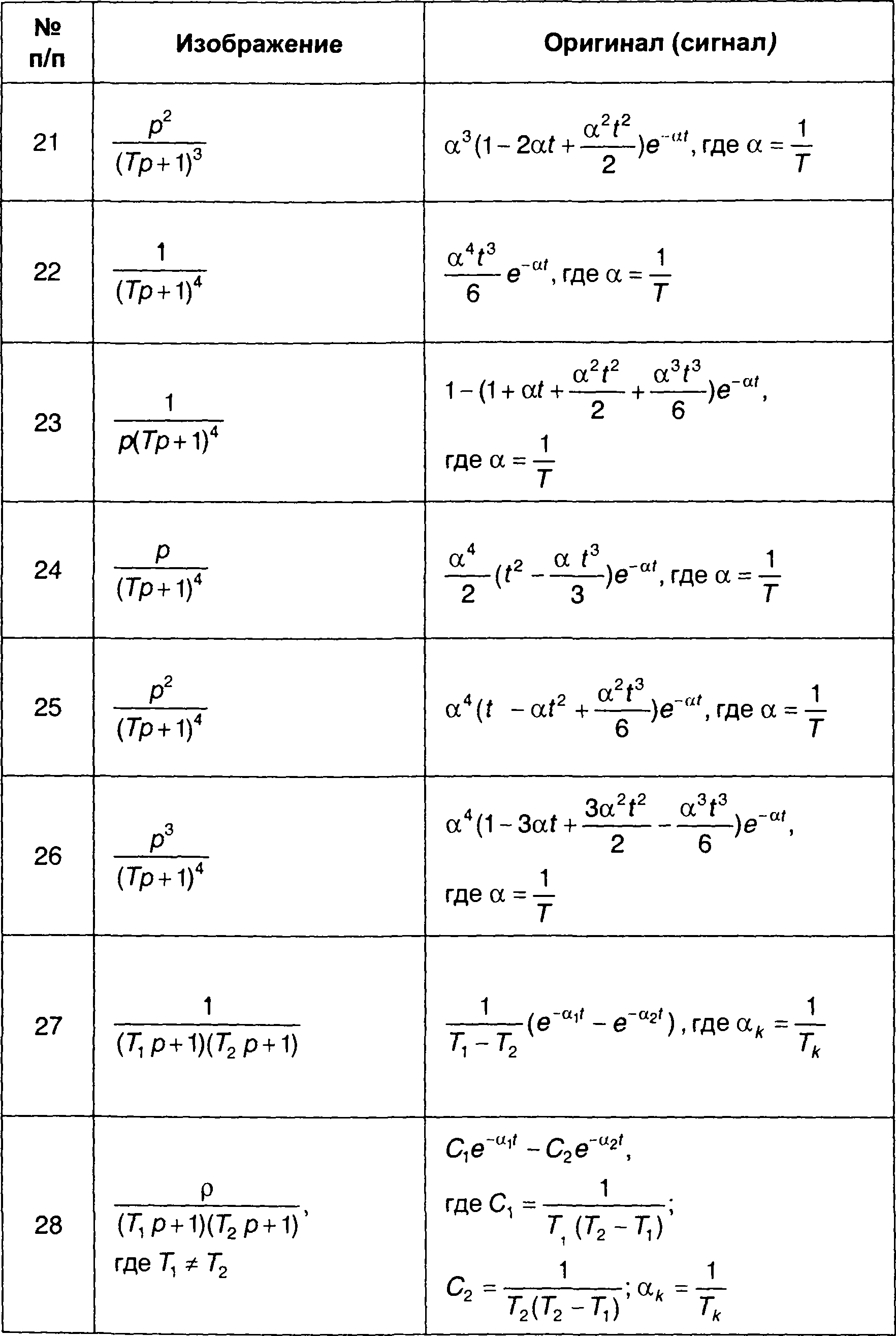
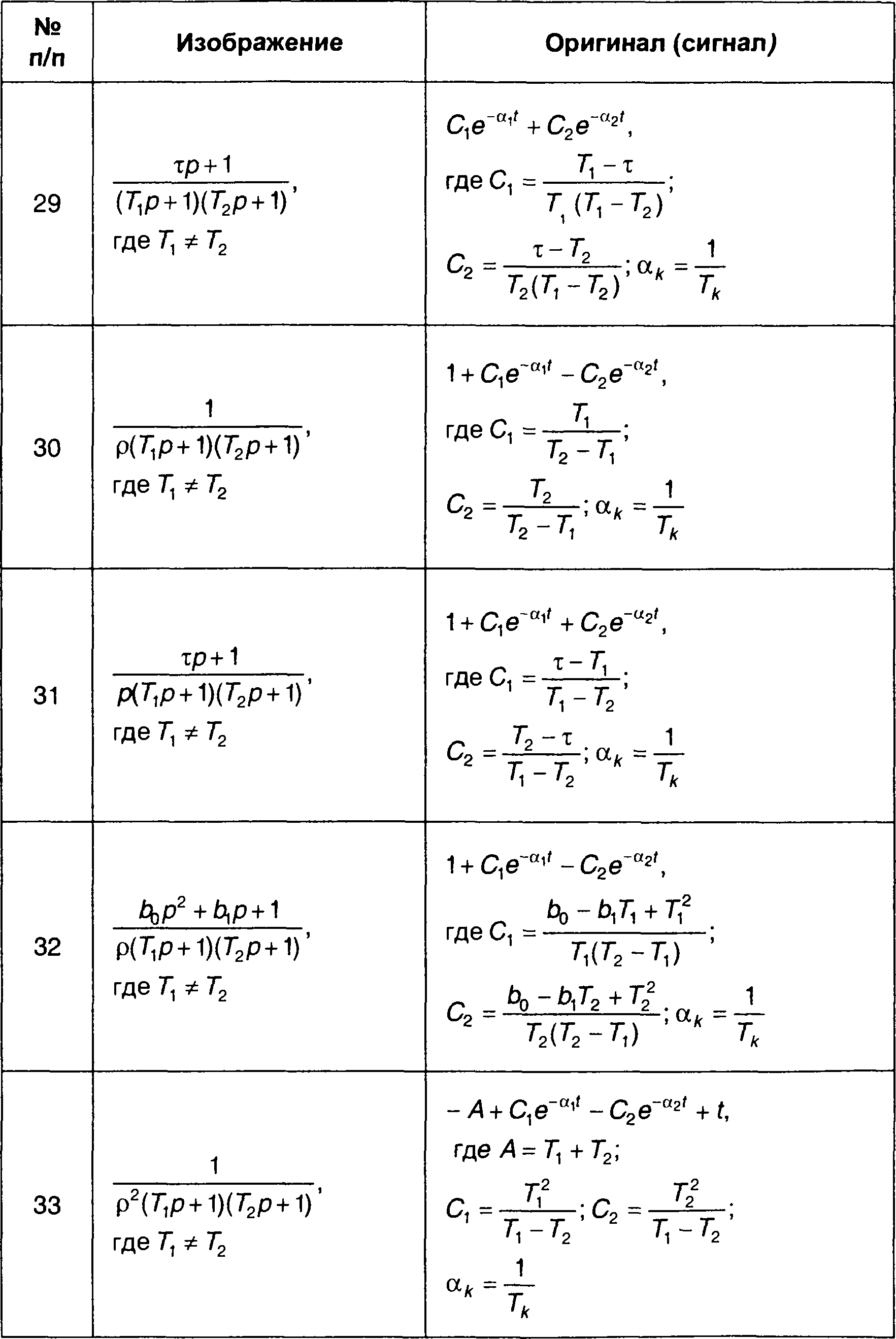
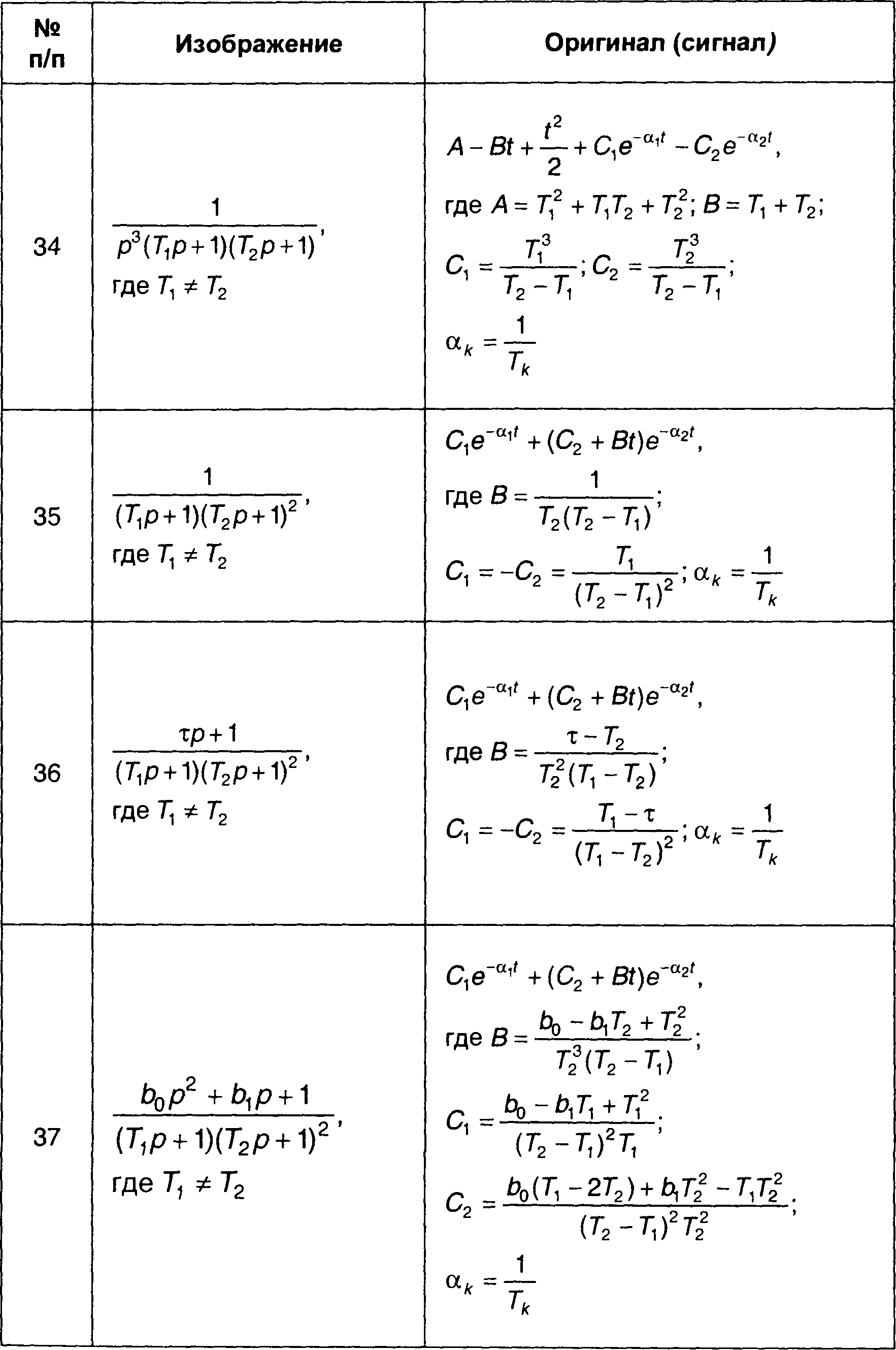
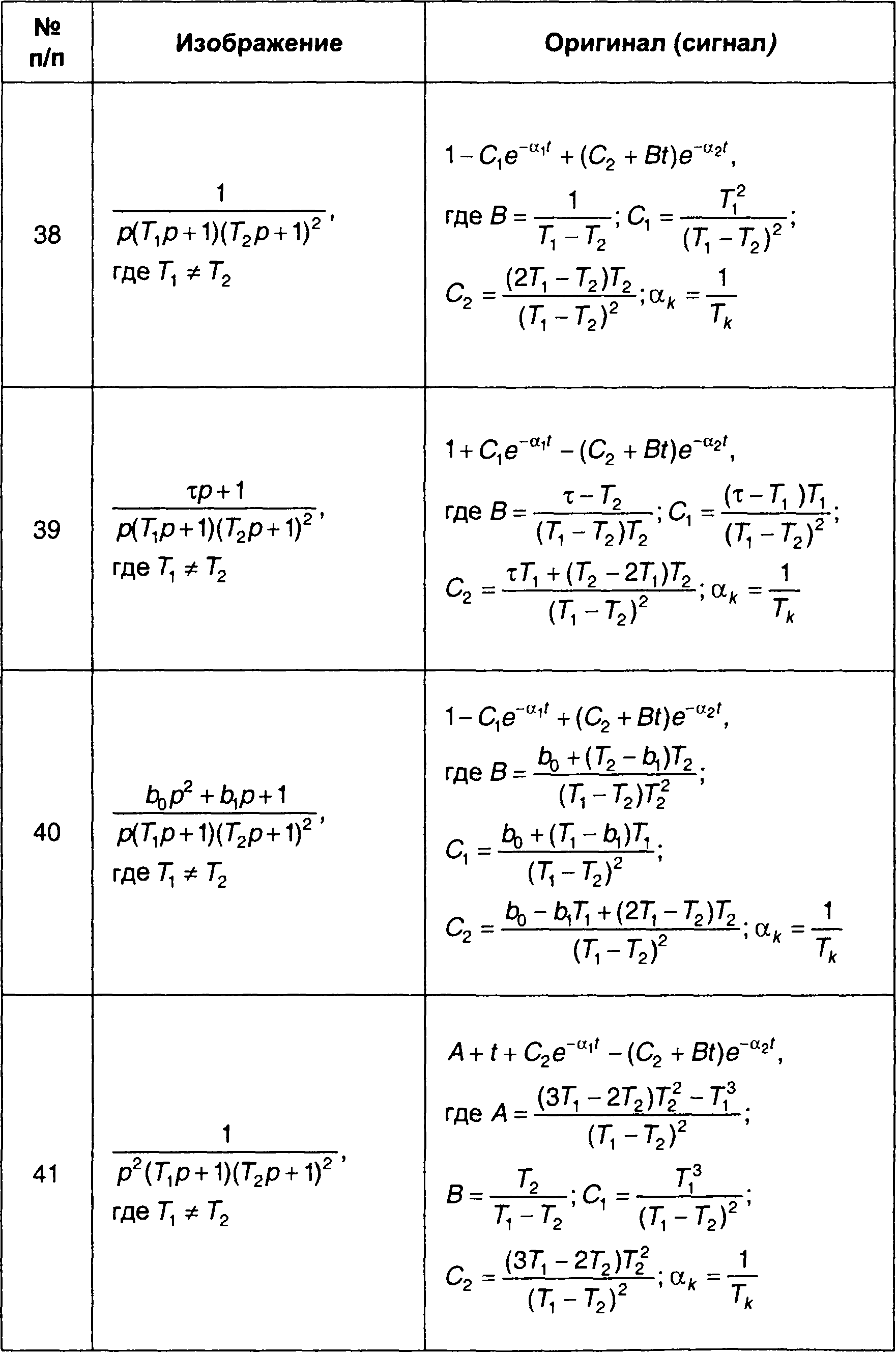
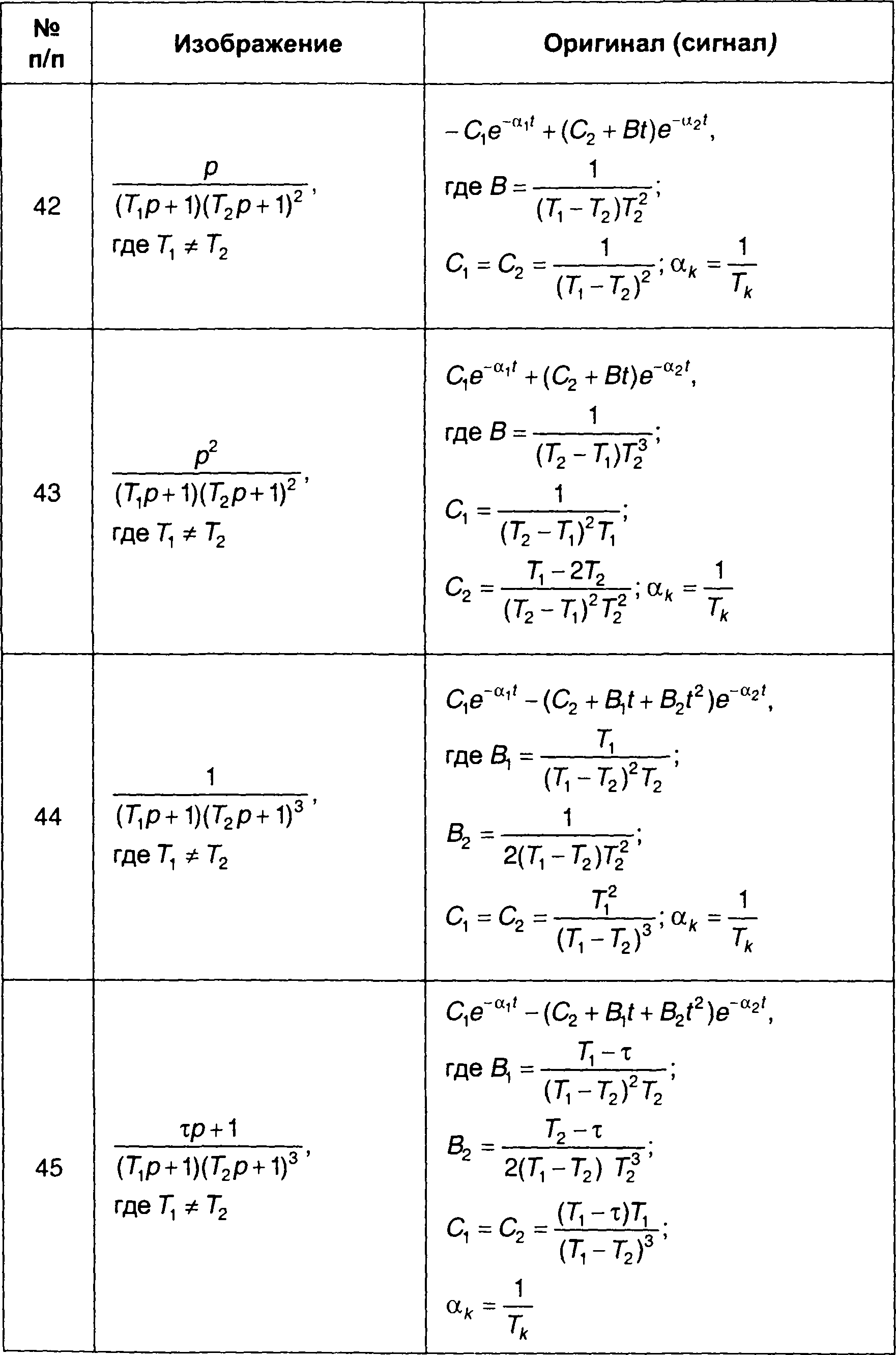
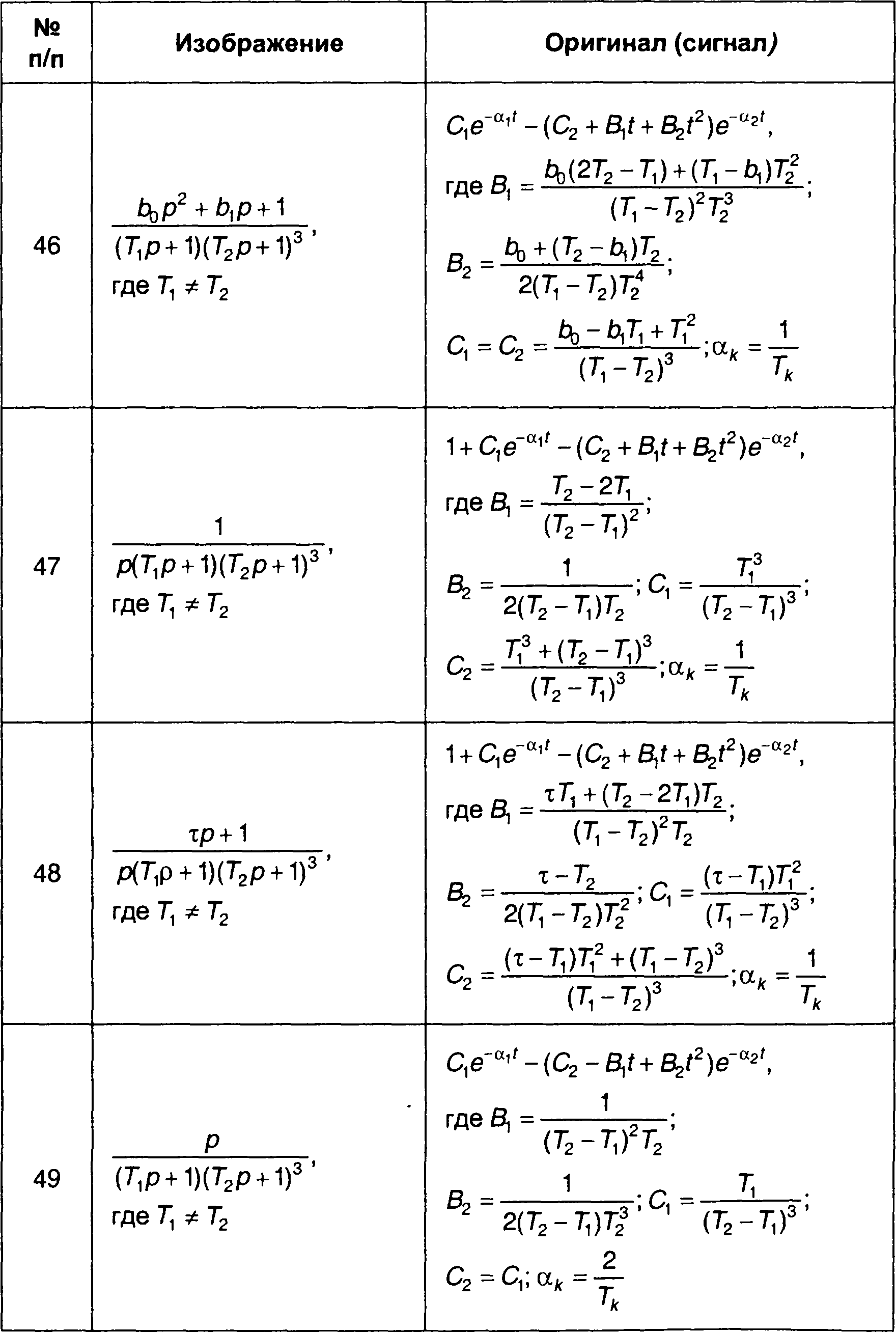
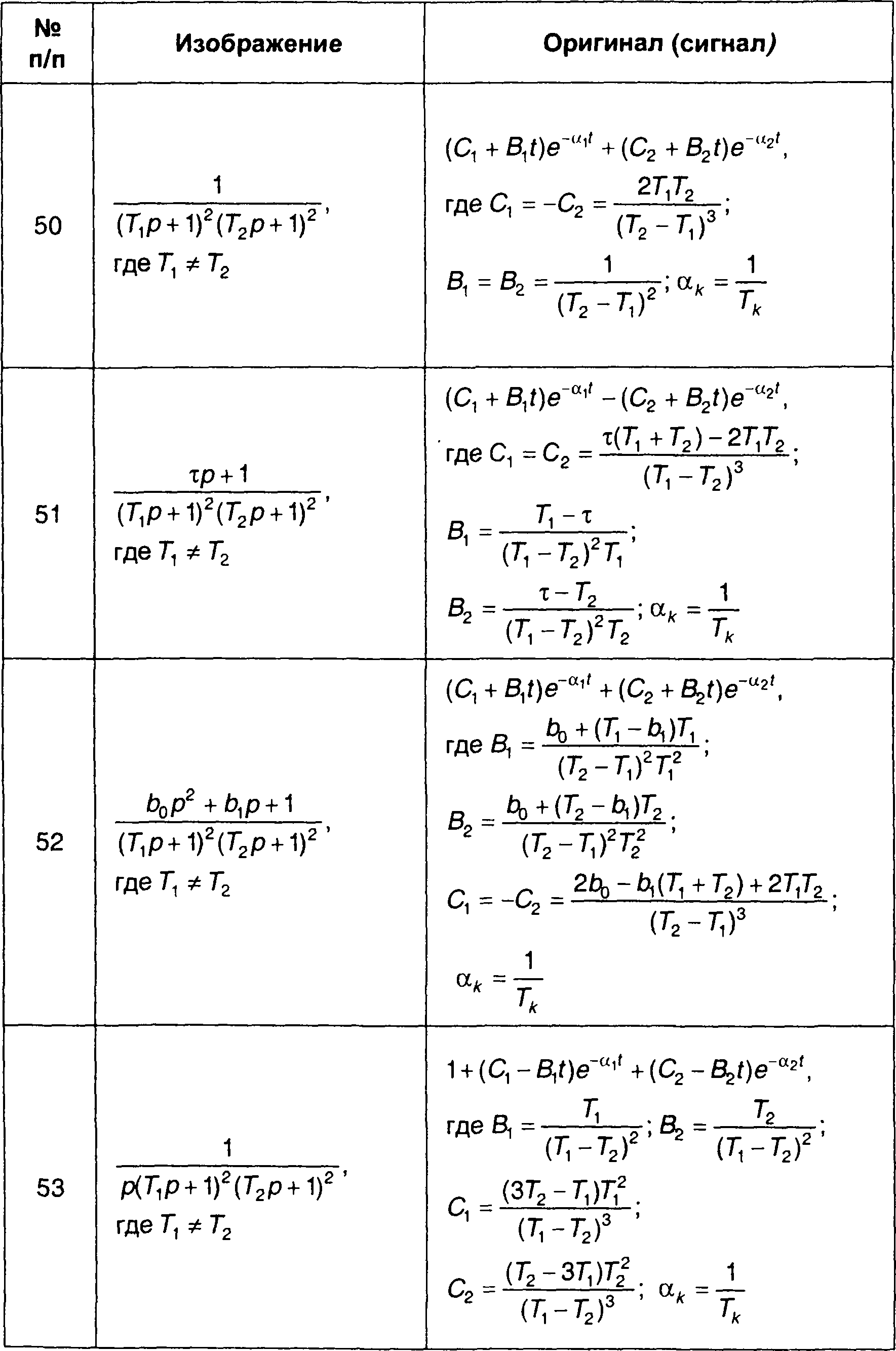
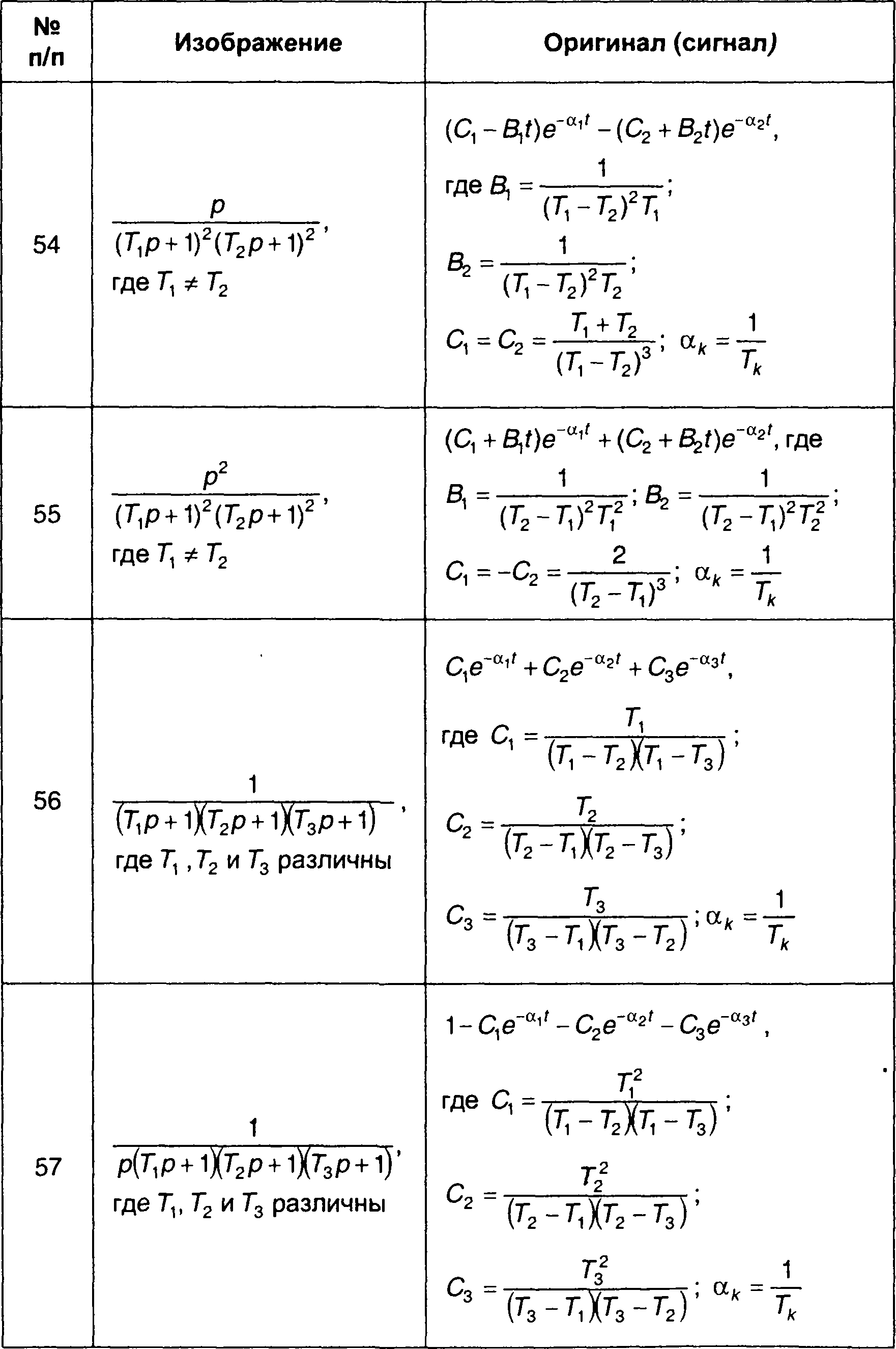
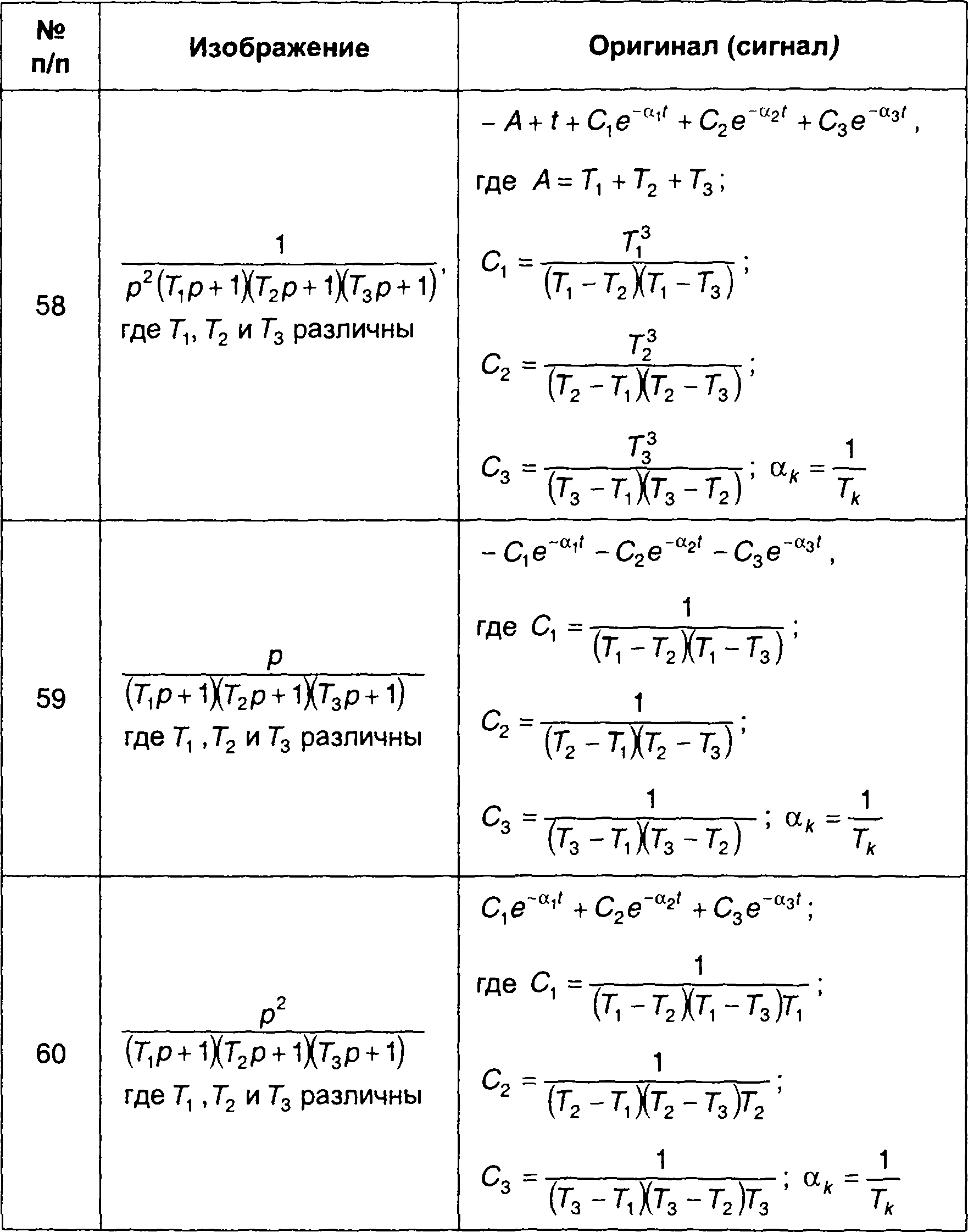
Раздел 5.

КОРРЕЛЯЦИОННЫЙ АНАЛИЗ СИГНАЛОВ

Понятие корреляции первоначально появилось применительно к случайным процессам. Позднее корреляционная функция была использована как характеристика детерминированных сигналов. Она описывает свойства сигналов во временной области, связана со спектральными характеристиками сигналов. Для радиолокаци­онных сигналов корреляционная функция является важнейшей ха­рактеристикой, определяющей потенциальные возможности раз­решения системы.

5.1. Корреляционные функции периодических сигналов

Корреляционная функция периодического сигнала s(t), имеюще­го период Т, определяется выражением

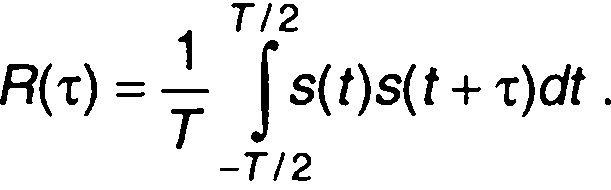(5.1)

Корреляционная функция одного сигнала называется автокор­реляционной функцией.

При т = 0 автокорреляционная функция

(5.2)

равна средней мощности сигнала. Нормированная величина

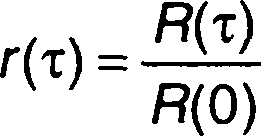
носит название нормированной корреляционной функции.

В качестве примера рассмотрим автокорреляционную функцию гармонического сигнала

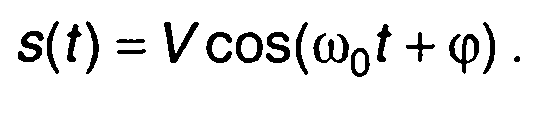
Она определяется как

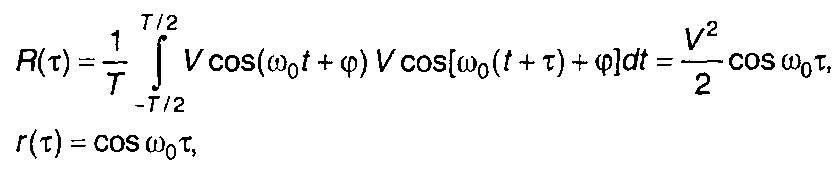
где Т = 2 π/ω₀.

Как следует из полученного результата, автокорреляционная функция гармонического сигнала представляет косинусоидальную функцию переменной т с тем же периодом и амплитудой, равной средней мощности сигнала.

Очевидно такую же автокорреляционную функцию имеют все гармонические сигналы той же частоты независимо от их началь­ной фазы.

Корреляционная функция периодических сигналов s₁(t) и s₂(t), имеющих одну и ту же частоту ω_о (период Т = 2π/ ω₀), определяется выражением

(5.3)

называется взаимной корреляционной функций. При τ = 0 она рав­на взаимной мощности сигналов

(5.4)

Нормированная взаимная корреляционная функция определяет­ся как

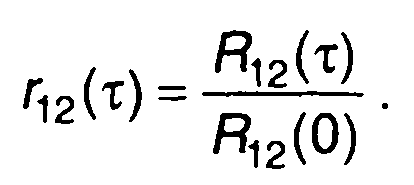
В качестве примера рассмотрим взаимную корреляционную функцию гармонических сигналов

Если изменить порядок следования рассматриваемых функций под знаком интеграла, получим

5.2. Соотношение между корреляционной функцией и спектром периодического сигнала

Соотношение между автокорреляционной функцией периодиче­ского сигнала и его спектральной плотностью мощности описывается рядом Фурье. Чтобы получить его, запишем выражение для периоди­ческого сигнала s(t) с периодом Т = 2π/ω₀ в виде ряда Фурье

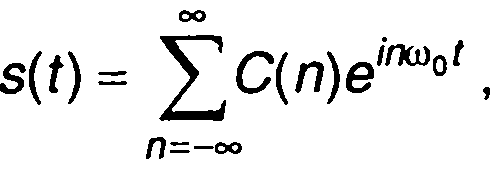(5.5)

где

(5.6)

Подставляя (5.5) в выражение для автокорреляционной функ­ции, получим

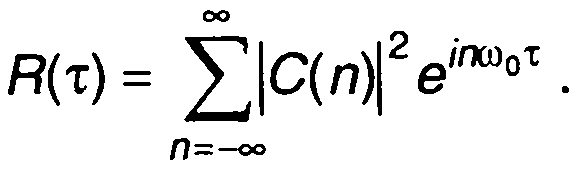(5.7)

Выражение (5.7) представляет ряд Фурье, в который расклады­вается автокорреляционная функция сигнала. Коэффициенты ряда Фурье определяются как

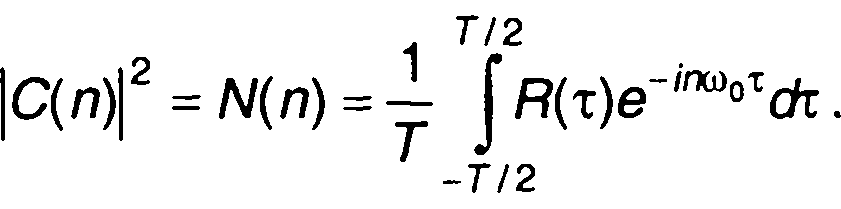(5.8)

При т = О

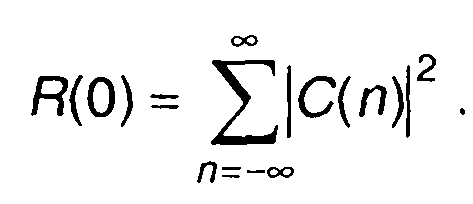(5.9)

Величина R(0) описывает среднюю мощность сигнала, │С(п)│²

характеризует распределение мощности сигнала по частоте, пред­ставляет спектральную плотность мощности. Как следует из запи­санных выражений, спектр является дискретным, включает состав­ляющие, описывающие мощности гармоник на частотах, кратных частоте сигнала.

С учетом четности автокорреляционной функции выражения (5.7) и (5.8) можно записать в виде

(5.10)

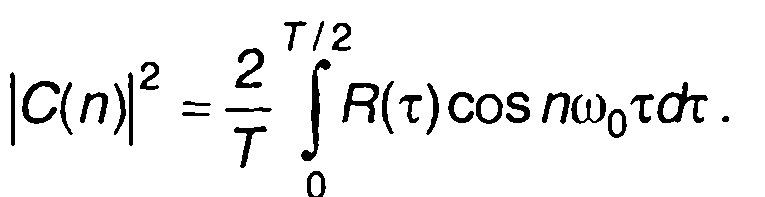(5.11)

Переходя к тригонометрическому ряду Фурье, получим

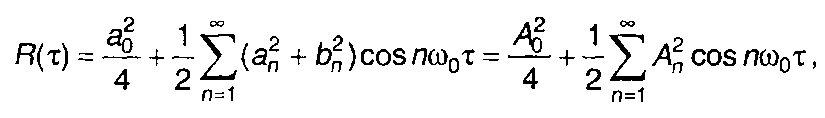(5.12)

где

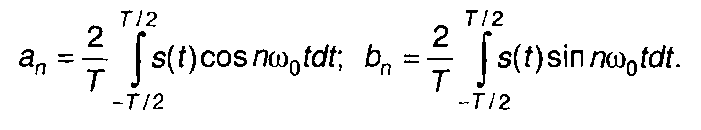
При т = 0 имеем

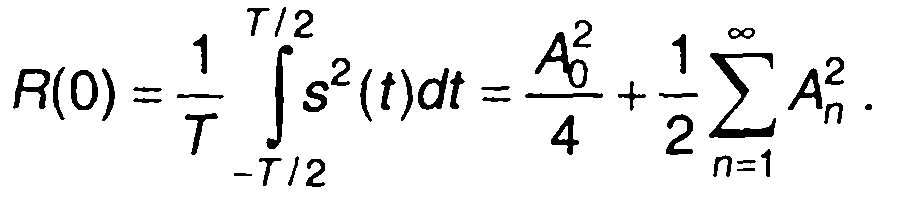(5.13)

Выражение (5.13) представляет равенство Парсеваля для пе­риодического сигнала.

Как следует из записанных выражений, автокорреляционная функция периодического сигнала является периодической функ­цией τ.

Соотношения между взаимной корреляционной функций перио­дических сигналов, имеющих один и тот же период, и их спектрами могут быть получены аналогично (5.7) и (5.8).

(5.14)

(5.15)

Величина C*₁(n)C₂(n) = N₁₂(n) представляет взаимный спектр мощности сигналов S₁(t) и s₂(t).

5.3. Корреляционные функции непериодических сигналов

Корреляционная функция непериодического сигнала определя­ется выражением

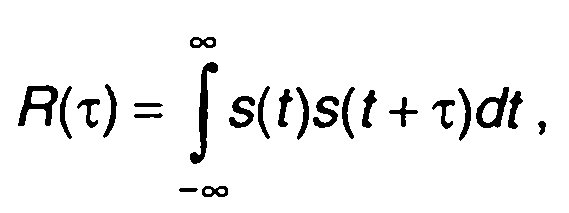(5.16)

где τ- смещение во времени.

Для действительного сигнала корреляционная функция является действительной четной функцией

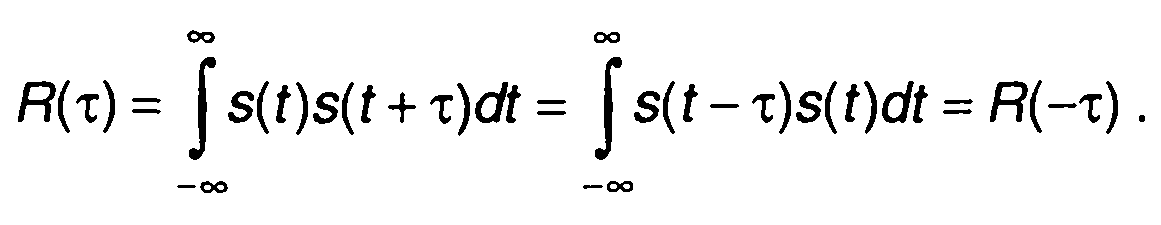(5.17)

Максимального значения корреляционная функция достигает при τ = 0. К этому выводу можно придти, рассмотрев выражение

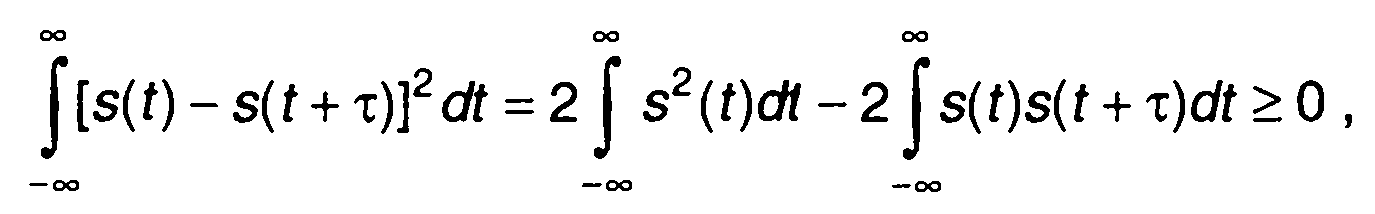
из которого следует:

R(0) - R(т) ≥ 0 или R(0)≥R(τ).

Корреляционная функция непериодического сигнала при т = 0 равна энергии сигнала

Рис. 5.1

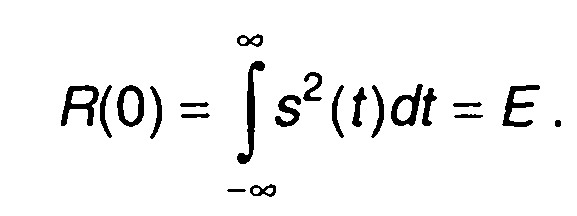(5.18)

Нормированная корреляционная функция непериодического сигнала определяется как

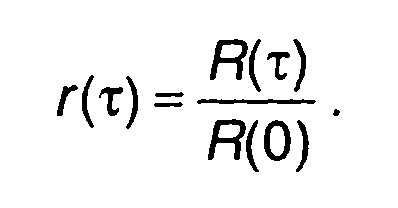
В качестве примеров рассмотрим корреляционные функции не­которых сигналов, описанных в табл. 3.1.

1. Прямоугольный импульс (табл. 3.1, п. 1), рис. 5.1.

При τ > 0

2. Экспоненциальный импульс (табл. 3.1, п.8), рис. 5.2.

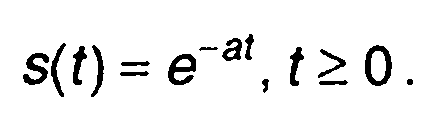
При τ > 0

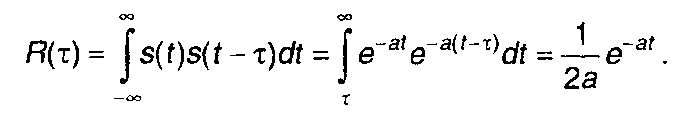
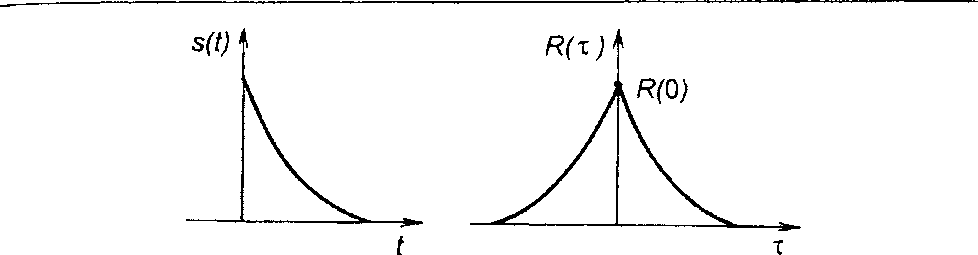
Рис.5.2.

3. Гауссов импульс (табл. 3.1, п. 15), рис. 5.3.

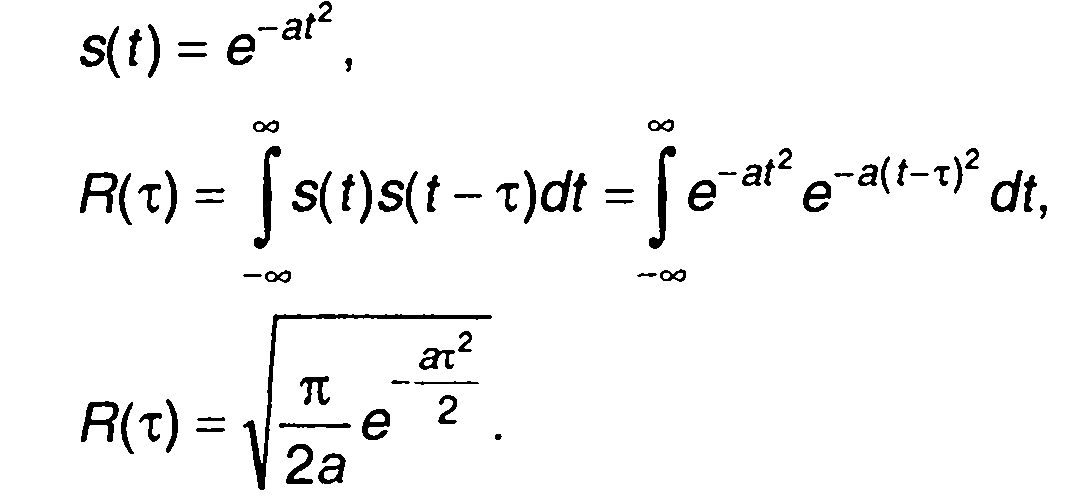
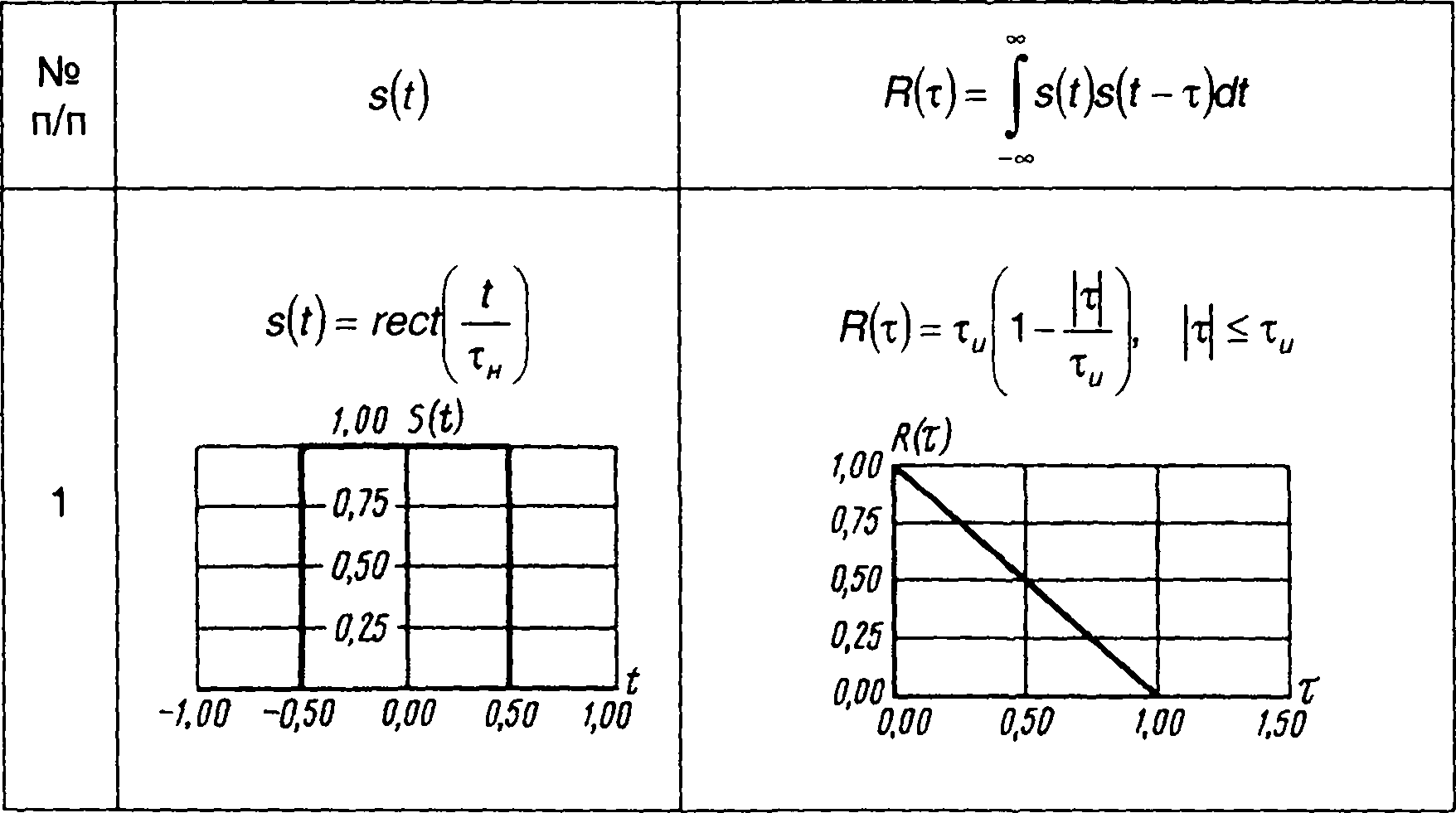
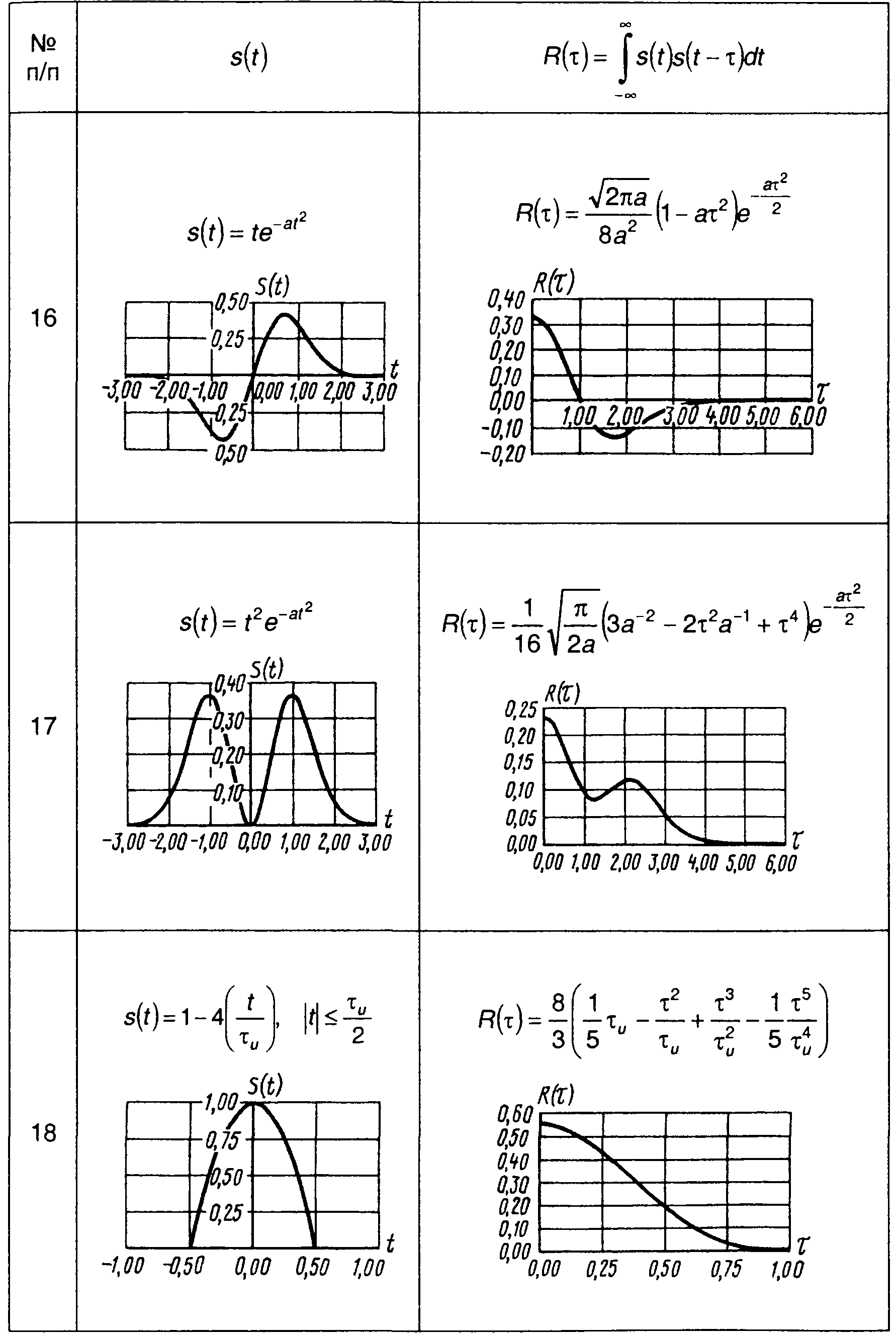
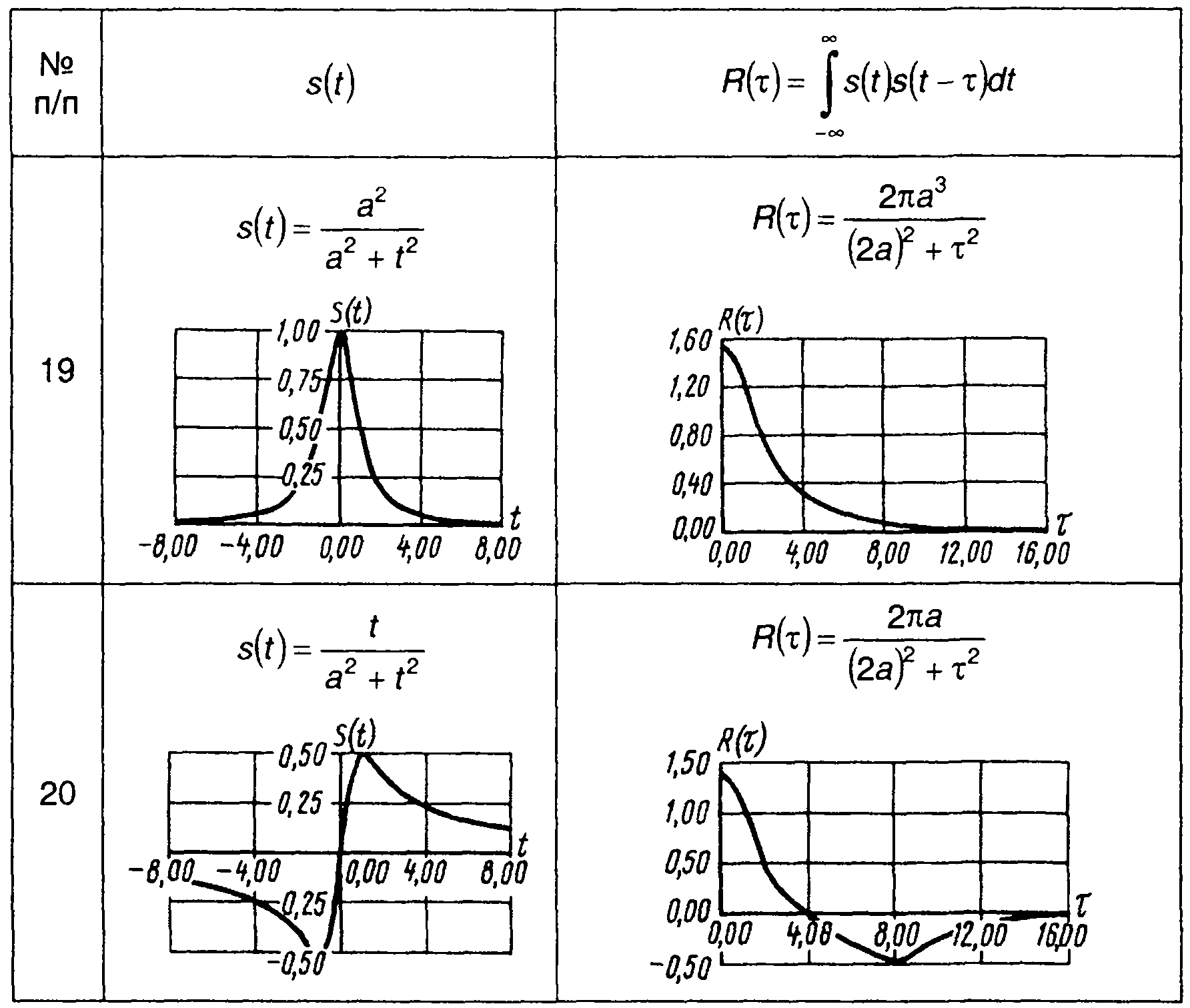
Корреляционные функции непериодических сигналов, приведен­ных в табл. 3.1, сведены в табл. 5.1. Так как корреляционная функ­ция является четной, графики построены только для τ > 0.

4. Пачка из двух прямоугольных импульсов (рис. 5.4).

При т>0

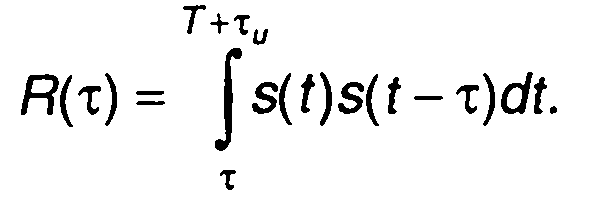
на интервале 0 < τ < τ_u.

Рис. 5.3

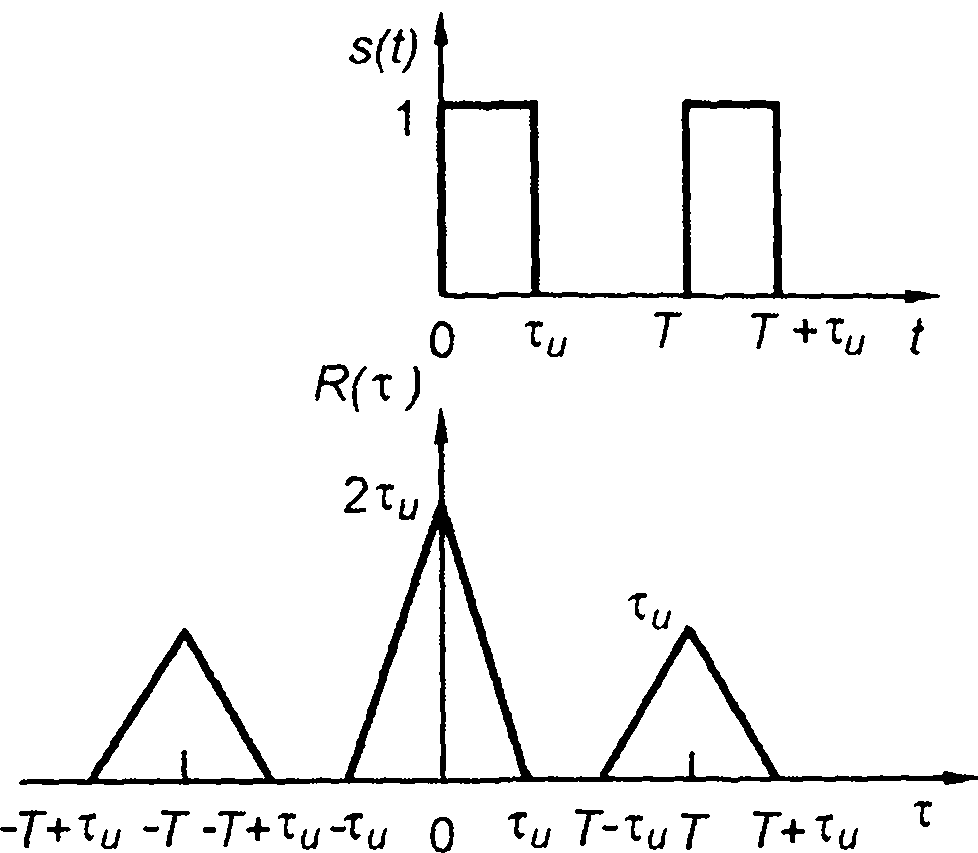
Рис. 5.4

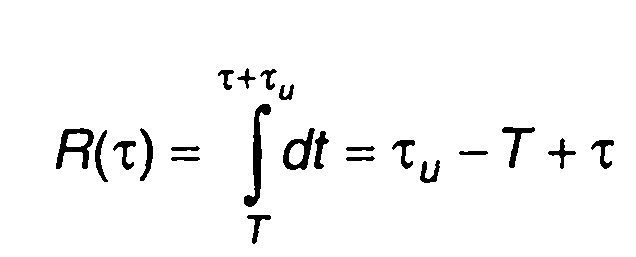на интервале τ_и ≤ т ≤ Т.

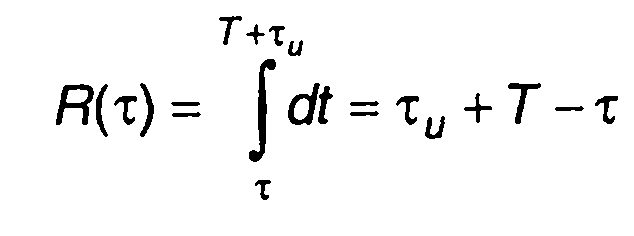на интервале Т ≤τ≤Т + τ_и.

Таблица 5.1.

Корреляционные функции сигналов

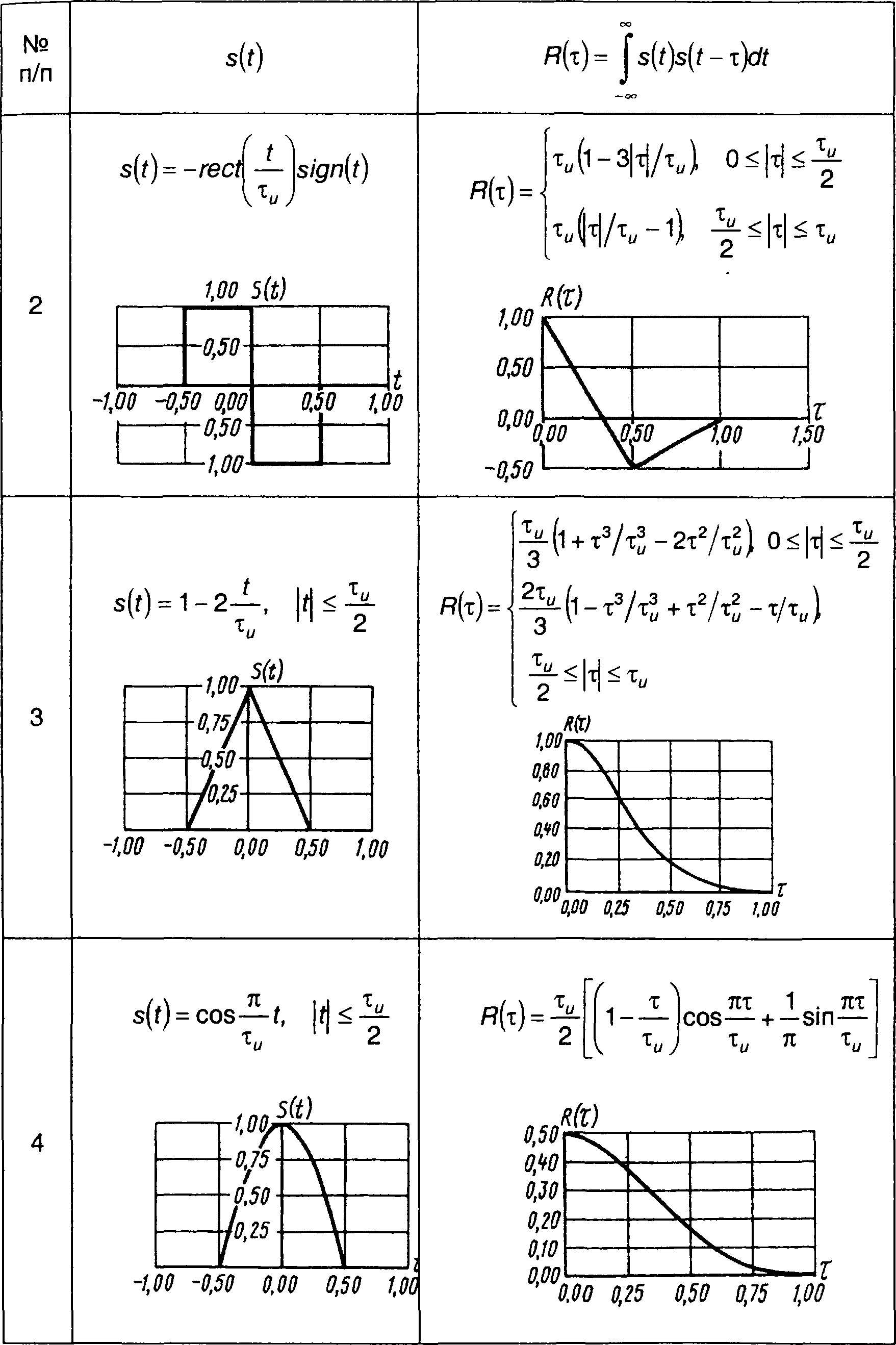
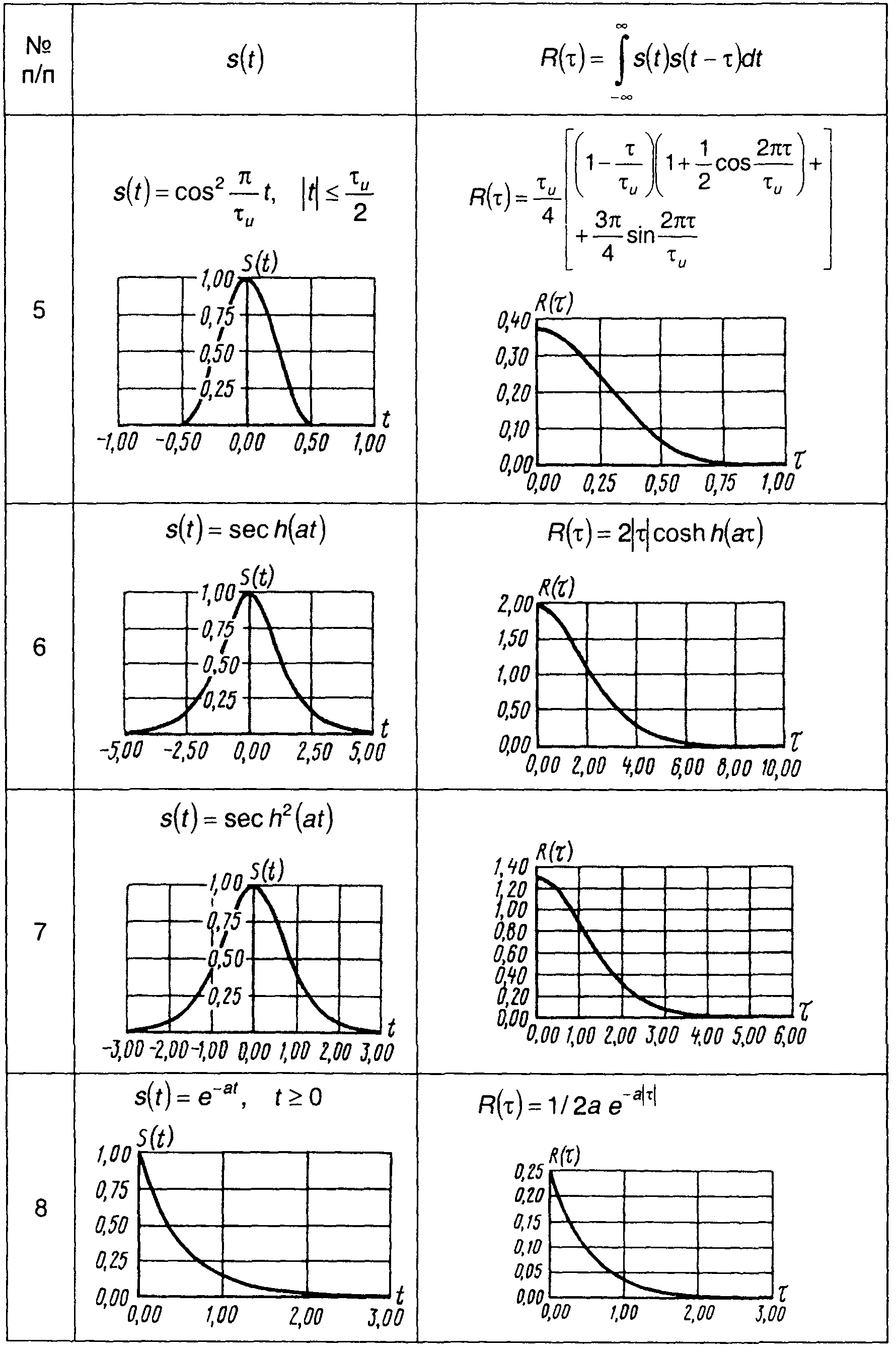
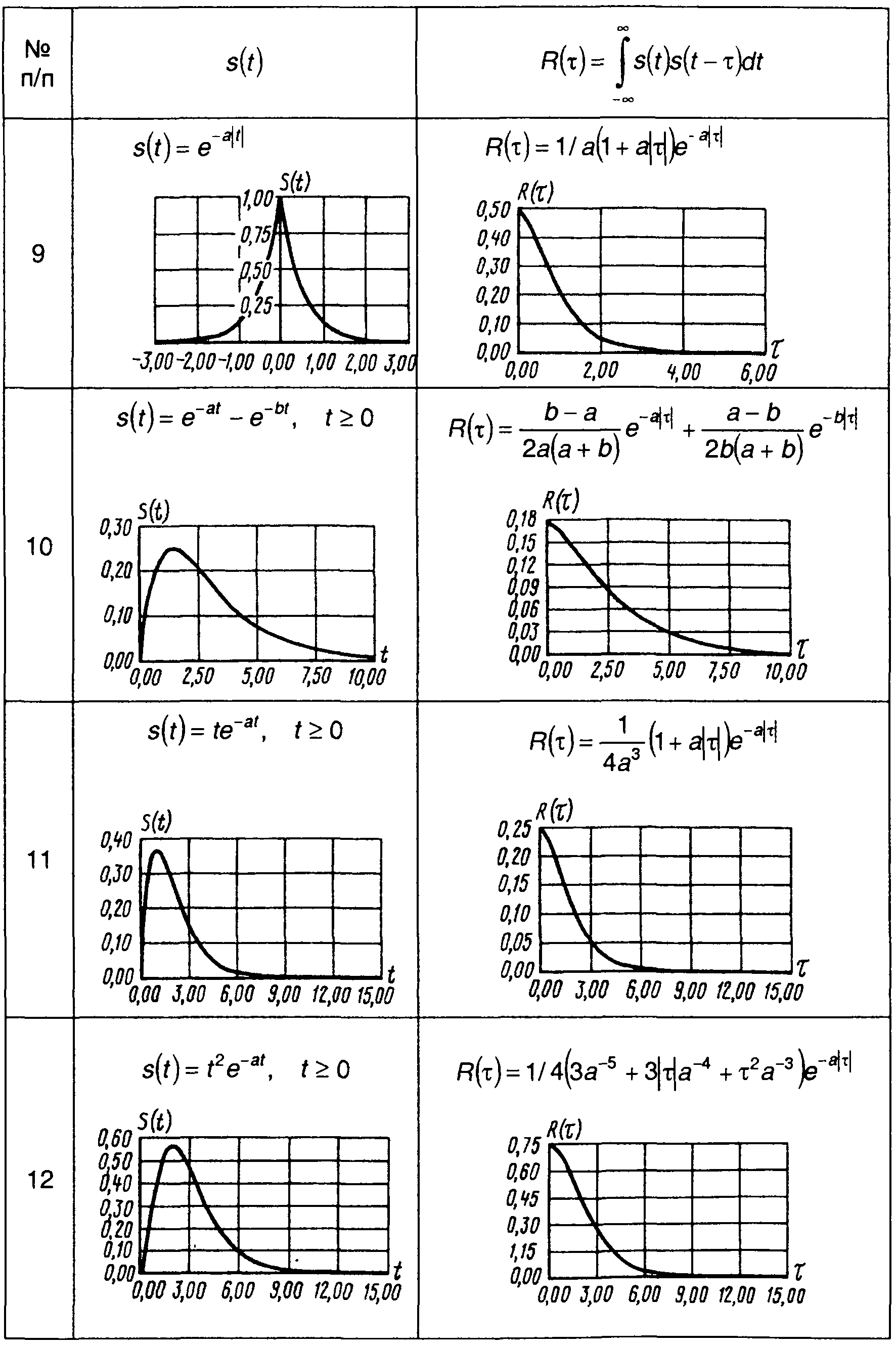
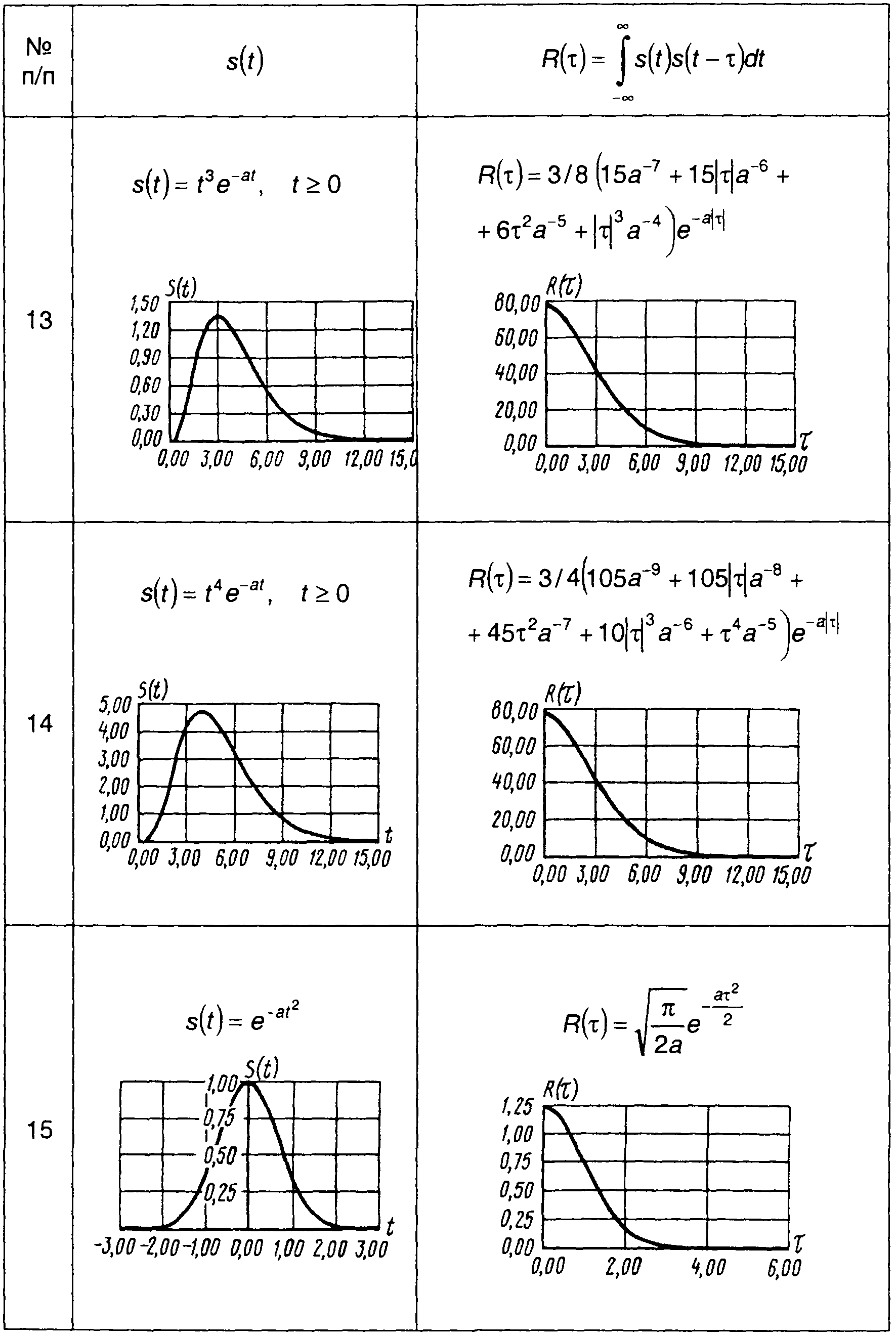
4. Пачка из N прямоугольных импульсов (рис. 5.5).

При τ>0

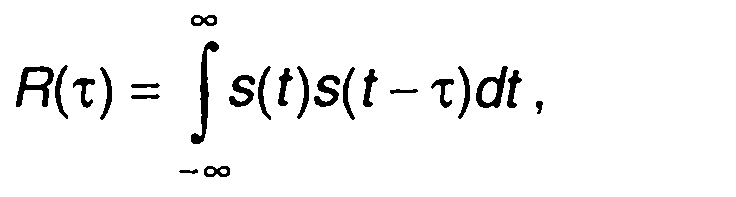
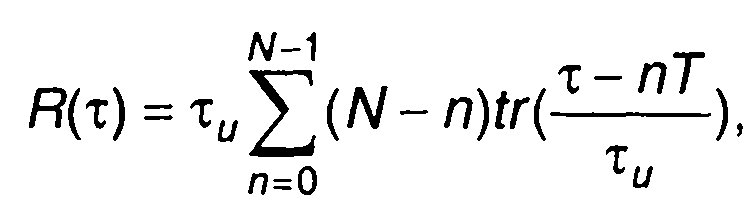
где tr(x) - треугольная функция;

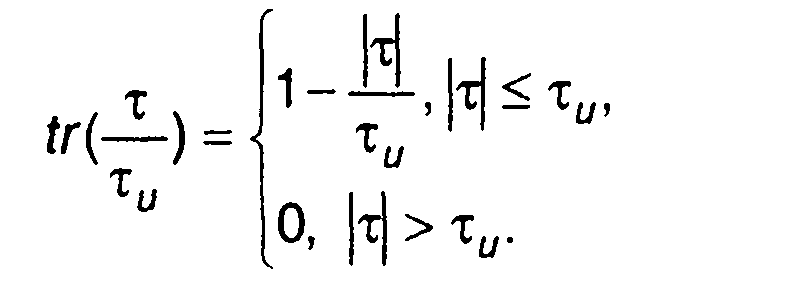
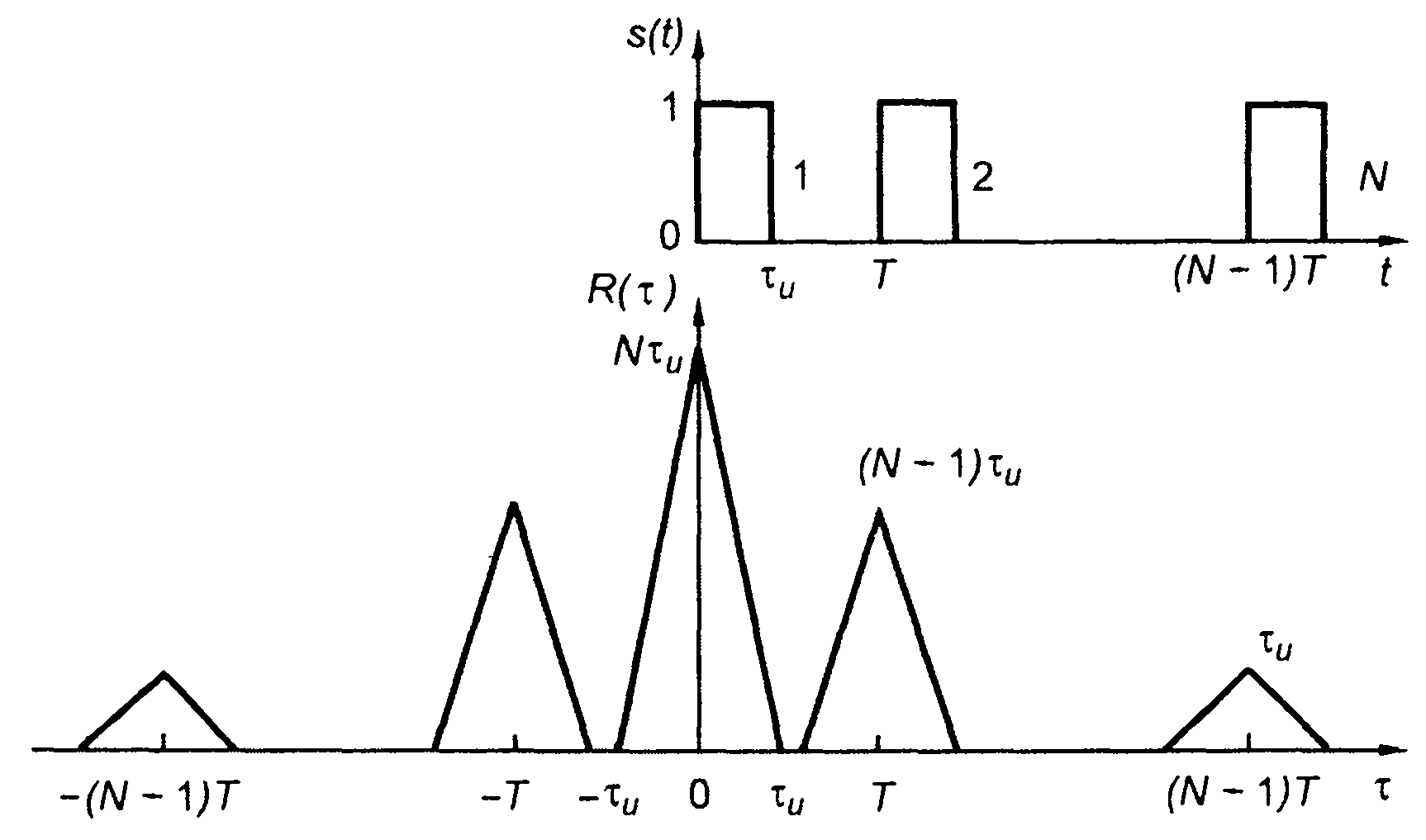
Рис. 5.5

Сравнивая выражения для автокорреляционных функций оди­ночных и периодических сигналов одного и того же вида, отметим, что при длительности сигнала значительно меньшей периода авто­корреляционную функцию периодического сигнала можно получить, взяв автокорреляционную функцию одиночного сигнала с коэффи­циентом 1 /T - периодическим ее повторением на оси т.

Корреляционная функция двух непериодических сигналов S₁(t) и S₂(t) определяется выражением

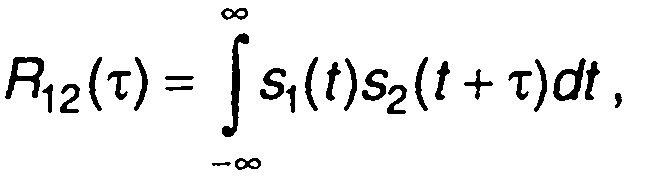(5.19)

где τ - смещение одного сигнала относительно другого во времени.

Выражение (5.19) имеет смысл только для сигналов, имеющих ограниченную энергию, для которых выполняются неравенства:

При т = 0

определяет взаимную энергию сигналов.

Нормированная взаимная корреляционная функция определяет­ся как

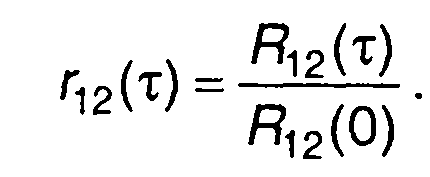(5.20)

Как и для периодических сигналов, если корреляционная функ­ция определена для двух сигналов, она называется взаимной кор­реляционной функцией, в отличие от автокорреляционной, опреде­ляемой для одного сигнала.

Для взаимной корреляционной функции имеет значение порядок следования функций под знаком интеграла. Для R₁₂(τ) и R₁₂(τ) получим следующее соотношение:

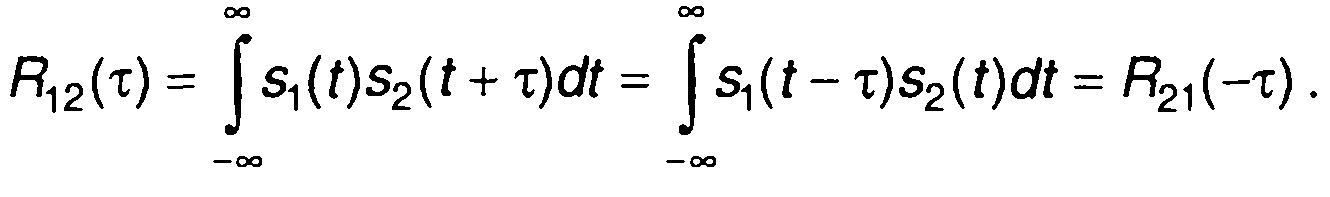(5.21)

Примеры взаимных корреляционных функций.

1. Сигналы - экспоненциальный и прямоугольный импульсы (рис. 5.6,а.)

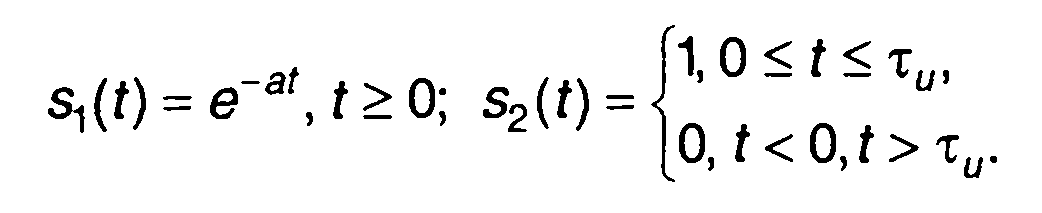
При τ<0

При τ>0

Если изменить порядок следования функций в выражении для корреляционной функции

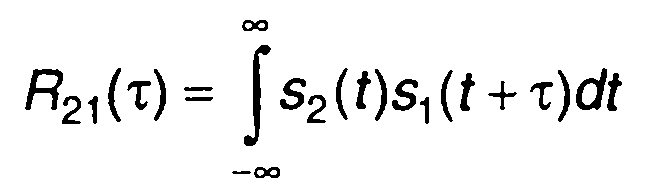
получим при τ<О

равно R₁₂(τ) при τ > 0.

При τ > О

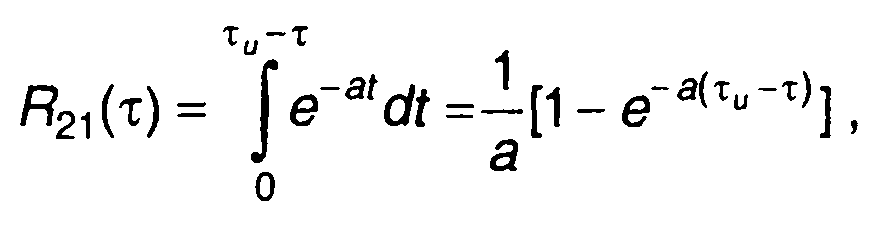
равно R₁₂(τ) при τ<0.

Графики R₁₂(τ) и R21 (τ) приведены на рис. 5.6,6.

2. Сигналы - треугольный и прямоугольный импульсы (рис. 5.7,а.)

Рис. 5.6

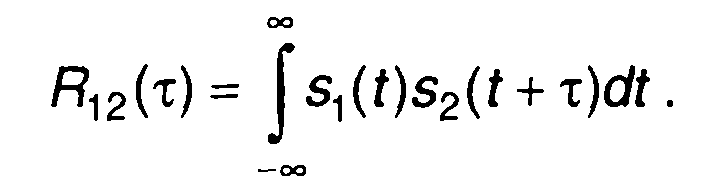
При τ < 0

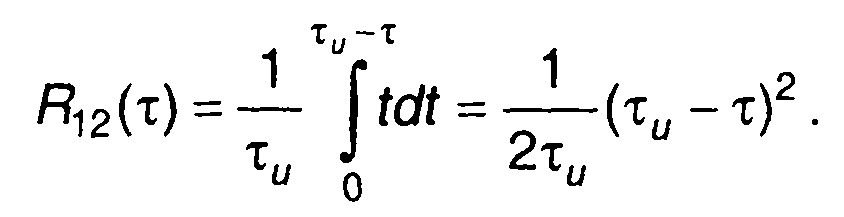
При τ > 0

Изменяя порядок следования функций, получаем.

При т < 0

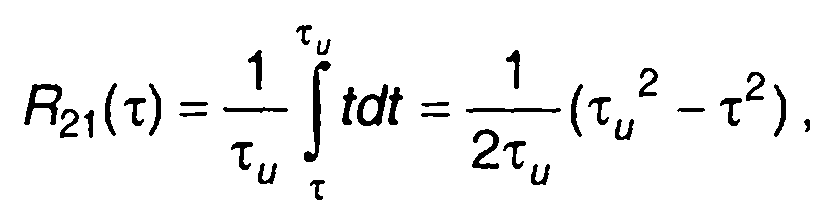
эта функция равна R₁₂(τ) при. τ >0.

При τ > О

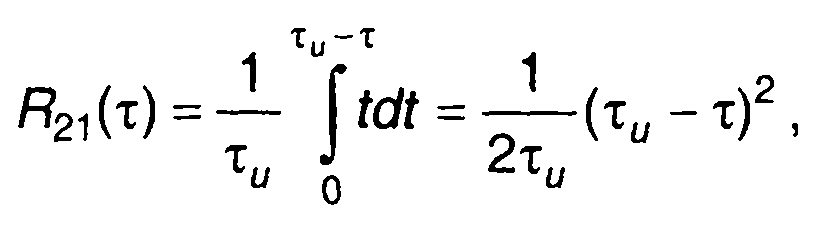
равна R₁₂(τ) при τ >0.

Графики R₁₂(τ) и R₂₁(τ) приведены на рис. 5.7,6.

5.4. Соотношение между корреляционной функцией и спектром непериодического сигнала

Автокорреляционная функция непериодического сигнала s(t) связана со спектральной плотностью энергии W(∞) преобразова­нием Фурье

(5.22)

Рис. 5.7

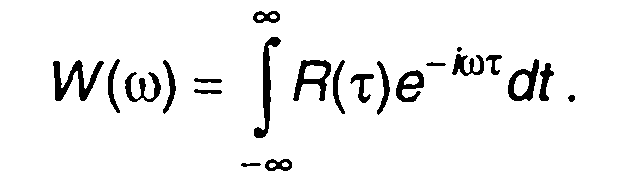(5.23)

Соотношение (5.23) может быть получено из (5.16)

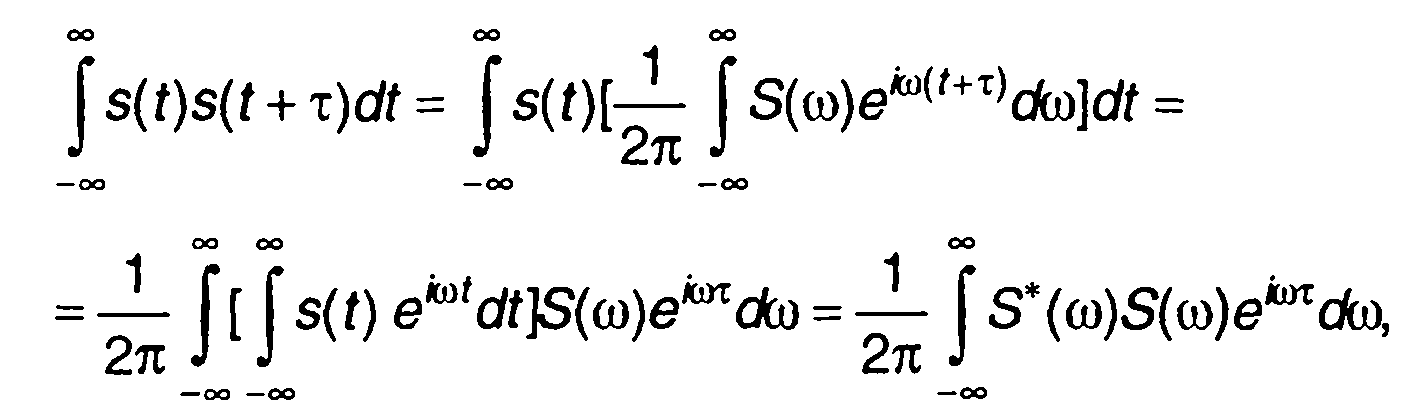(5.24)

Где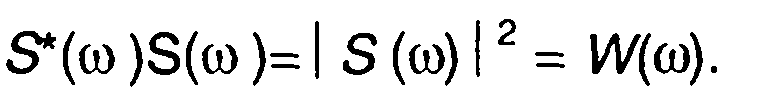

Учитывая четность функций R(т) и W(co), (5.22) и (5.23) можем записать в виде:

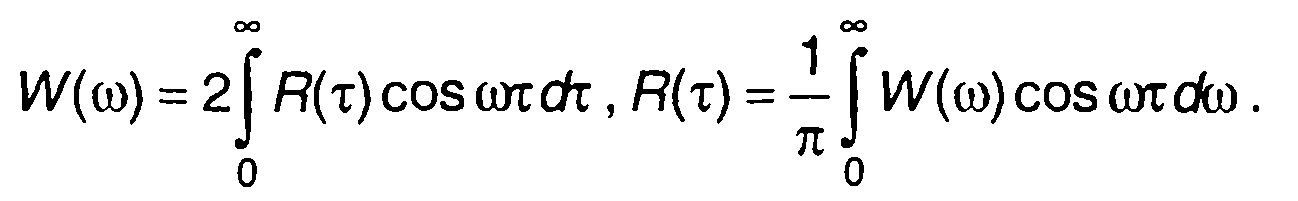(5.25)

При т = 0

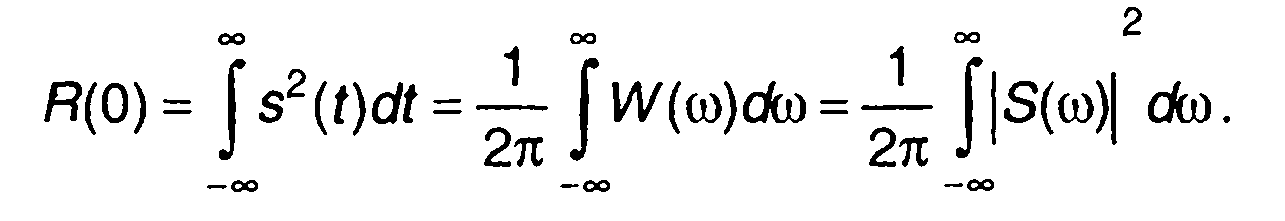(5.26)

Выражение (5.26) представляет равенство Парсеваля. Каждая из частей этого равенства определяет энергию сигнала. Как следу­ет из (5.26), энергия сигнала численно равна площади под кривой W(ω). Кривая W(ω) характеризует распределение энергии сигнала по частоте.

Так как преобразование Фурье автокорреляционной функции равно квадрату модуля спектральной плотности сигнала, то авто­корреляционная функция не содержит информации о фазовом спектре. Имея автокорреляционную функцию сигнала, можно вос­становить только амплитудный спектр, но нельзя получить фазово­го спектра сигнала.

Примеры определения автокорреляционных функций с исполь­зованием спектральных плотностей сигналов приведем для некото­рых сигналов, включенных в табл. 3.1.

1. Сигнал s(t) = sech(at), (табл. 3.1, п.6 ).

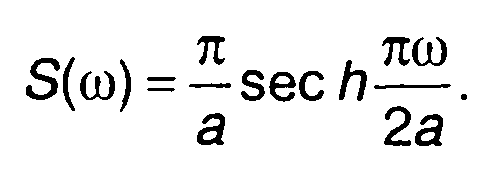
При т>0

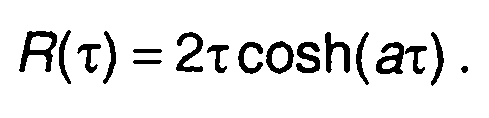
2. Сигнал s{t) = e^-at, t ≥ 0 , (табл. 3.1. п.8).

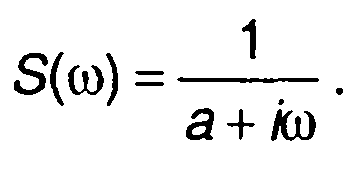
При τ ≥0

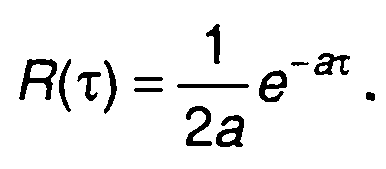
3. Сигнал s(t) = te^-at2 (табл. 3.1. п.16).

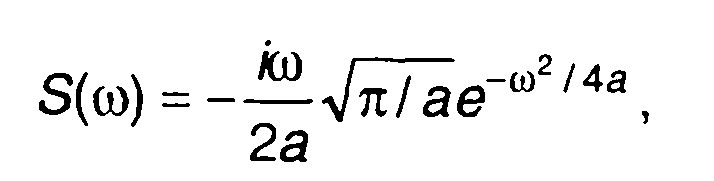
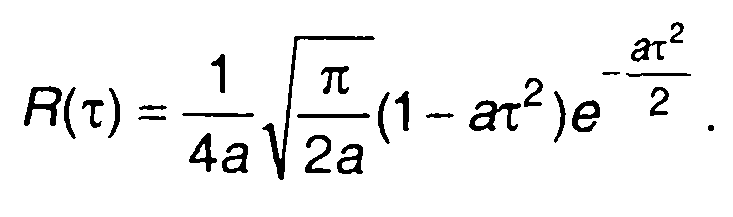
Аналогично (5.22) и (5.23) можно подучить соотношения, связы­вающие взаимную корреляционную функцию непериодических сиг­налов s-i(t) и S2(t) с взаимной спектральной плотностью энергии W₁₂( со)

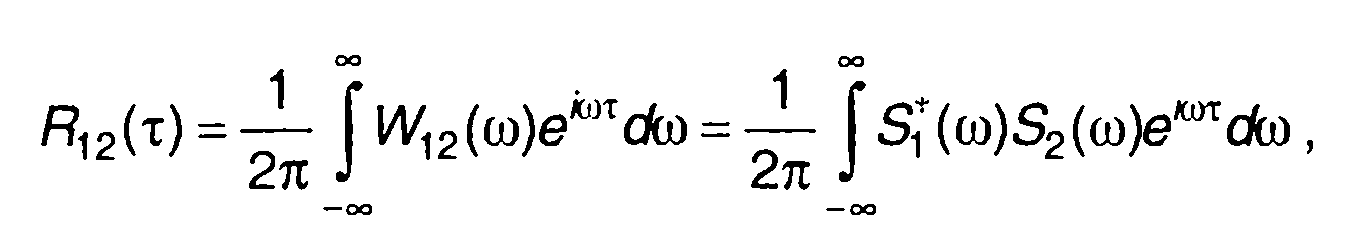(5.27)

(5.28)

5.5. Интервал корреляции и эффективная ширина спектра сигнала

Для каждой корреляционной функции непериодического сигнала можно определить такое минимальное значение смещения во вре­мени τ_k, при котором абсолютное значение корреляционной функ­ции будет меньше заданной величины (близко к нулю). Величину τ_k называют интервалом корреляции. Интервал корреляции пред­ставляет наибольший интервал задержки (смещения), на котором корреляционная функция имеет значение, существенное для ре­шаемой задачи.

Интервал корреляции, как и понятие корреляции, первоначально был введен в рассмотрение для случайных процессов (разд. 18). Для детерминированных сигналов он определяется по аналогии. В ряде практических приложений корреляционного анализа он оказывает­ся полезным понятием.

Наиболее часто используют следующие определения интервала корреляции.

1. Интервал корреляции, определяемый по заданному значению нормированной корреляционной функции

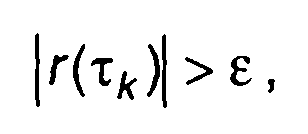(5.29)

где ε - заданное значение (например, ε = 0,05); τ_k- максимальный интервал, на котором выполняется записанное неравенство.

2. Интервал корреляции, определяемый значением интеграла нормированной корреляционной функции или ее абсолютного значения

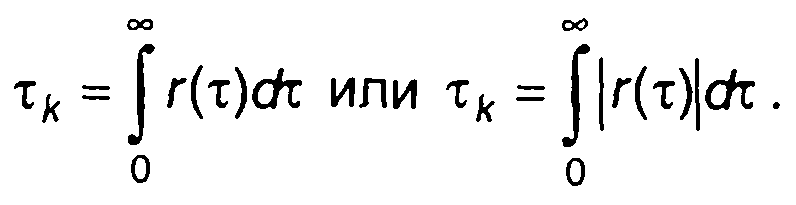(5.30)

При таком определении интервал корреляции численно равен основанию прямоугольника, высота которого равна максимальному значению нормированной корреляционной функции r(0) = 1, а пло­щадь равна площади под кривой r(т) или |r(т)|. Второе определе­ние интервала корреляции чаще используется при явно выражен­ном колебательном характере корреляционной функции.

3. Интервал корреляции, определяемый значением интеграла от квадрата нормированной корреляционной функции

(5.31)

Значения τ_к, определяемые из приведенных выражений, близки друг другу. Выбор их, как правило, диктуется удобством при реше­нии конкретной задачи.

Если для определения ширины корреляционной функции ис­пользуется понятие интервала корреляции, то для определения ширины спектра сигнала вводится понятие эффективной ширины спектра. Эффективную ширину спектра определим как длину наи­большего интервала на оси частот, на котором спектральная плот­ность энергии еще имеет существенное для решаемой задачи зна­чение.

При определении эффективной ширины спектра сигнала можно использовать, как и при определении интервала корреляции, не­сколько подходов.

1. Эффективная ширина спектра А определяется из условия, аналогичного (5.9), - максимальная полоса частот, внутри которой значение нормированной спектральной плотности энергии сигнала еще превосходят заданное значение

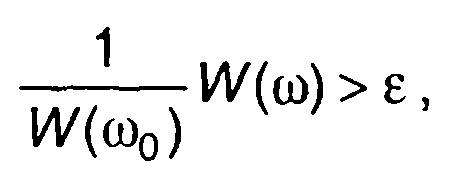(5.32)

2. Эффективная ширина спектра определяется заданным значе­нием интеграла нормированной спектральной плотности энергии сигнала

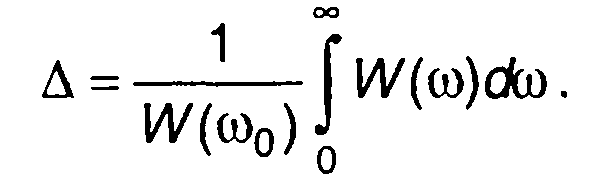(5.33)

Величина ∆ определяемая (5.33), представляет ширину равно­мерного спектра энергии сигнала, имеющего энергию, равную энер­гии рассматриваемого сигнала.

Раздел 6.

ДИСКРЕТИЗАЦИЯ И ВОССТАНОВЛЕНИЕ НЕПРЕРЫВНЫХ СИГНАЛОВ

Непрерывные сигналы могут задаваться выборочными значения­ми, взятыми через определенные интервалы времени. Такое пред­ставление непрерывного сигнала называется дискретизацией. Дис­кретизация сигнала позволяет сократить время работы канала пере­дачи информации, лежит в основе цифровой обработки сигналов.

Обратная операция - восстановление непрерывного сигнала по его дискретным значениям. В математическом плане она означает интерполяцию временной функции, описывающей сигнал, по ее выборочным значениям.

В разделе изложены методы анализа дискретных сигналов и восстановления непрерывных сигналов по их выборочным значе­ниям. Дискретизация и интерполяция, рассматриваемые примени­тельно к сигналам, могут быть использованы и в отношении раз­личных характеристик сигналов.

6.1. Дискретные и цифровые сигналы

Передача информации с помощью сигналов может произво­диться непрерывно или в некоторые фиксированные моменты вре­мени. В зависимости от характера передачи информации различа­ют непрерывные и дискретные сигналы. Непрерывные (аналого­вые) сигналы повторяют закон изменения физических величин, ин­формацию о которых они содержат, описываются непрерывными или кусочно-непрерывными функциями времени (рис.6.1,а). Дис­кретный сигнал представляет последовательность коротких им­пульсов, амплитуды которых соответствуют мгновенным значениям непрерывного сигнала или физической величины (рис. 6.1,6).

Дискретные сигналы чаще всего формируются при цифровой обработке для использования в ЭВМ: непрерывные сигналы дискретизируются во времени и квантуются по уровню, (рис. 6.1,б). Та­кие сигналы, представленные цифровыми кодами, называются цифровыми.

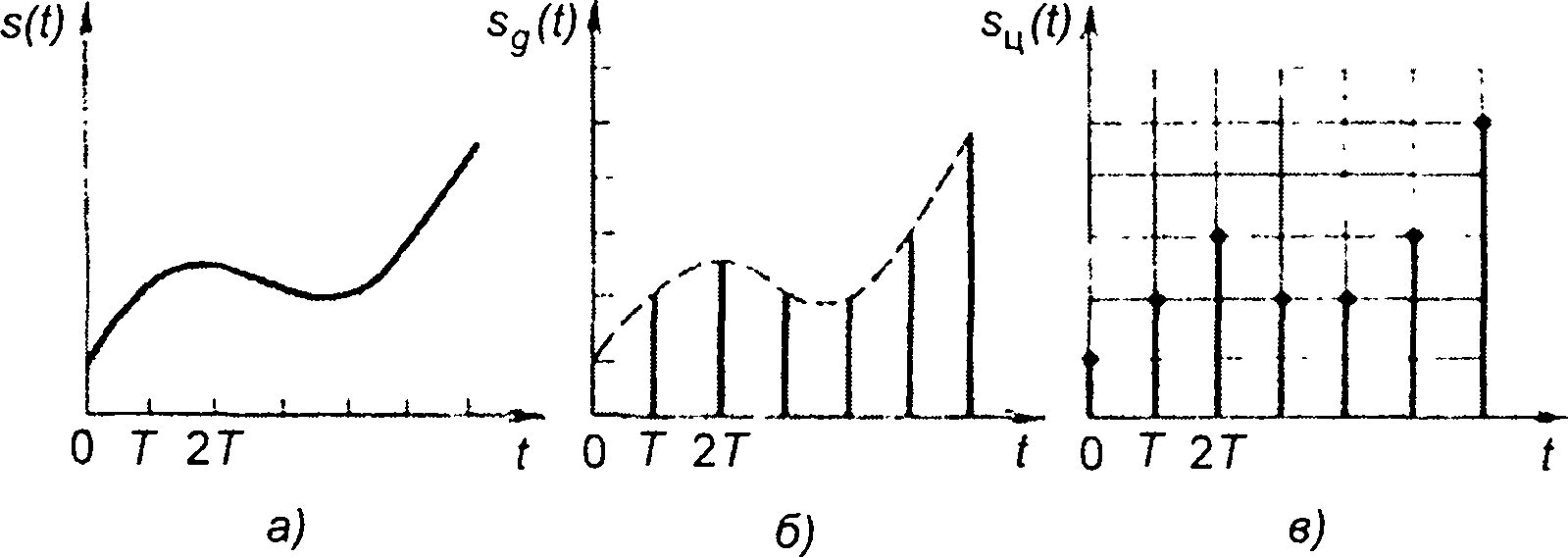
Рис. 6.1

При квантовании по уровню значение сигнала округляется до ближайшего дискретного значения. Ошибка, сопровождающая квантование, представляет случайную величину, не превышающую половину шага квантования. При постоянном шаге квантования распределение ошибки подчиняется равномерному закону. После­довательность ошибок при каждом шаге дискретизации аналогово­го сигнала во времени можно рассматривать как случайный дис­кретный процесс. Вследствие этого обычно квантованный сигнал представляют в виде суммы дискретного сигнала и шума квантова­ния, а анализ цифровых сигналов сводится к анализу прежде всего дискретных сигналов, значения которых соответствуют значениям исходного непрерывного сигнала.

6.2. Спектр дискретного сигнала

При дискретизации непрерывный сигнал заменяется совокупно­стью его значений, взятых в заданные моменты времени. Как пра­вило, интервал между выбранными моментами времени интервал дискретизации - берется постоянным. Это условие предполагается и в дальнейшем. Выборка осуществляется с помощью стробирующего сигнала, представляющего последовательность импульсов малой длительности, в пределе - описываемых импульсной функ­цией. Примеры дискретных сигналов приведены в табл. 6.1.

Если непрерывный сигнал представлен выборочными значе­ниями, взятыми через заданный интервал времени, то получаю­щийся дискретный сигнал может быть записан в виде

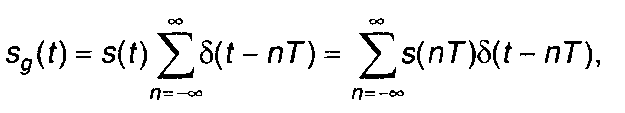(6.1)

где s(t) - непрерывный сигнал; T - период дискретизации.

Стробирующая последовательность δ-функций

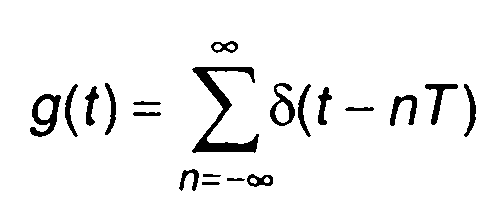(6.2)