ДЕТЕРМИНИРОВАННЫЕ СИГНАЛЫ 2 страница

Передача информации с помощью сигналов может произво­диться непрерывно во времени или в некоторые фиксированные моменты. В зависимости от характера передачи информации (не­прерывно или дискретно) различают непрерывные или аналоговые и дискретные сигналы. Аналоговые сигналы повторяют или зависят от закона непрерывного изменения физических величин, информа­цию о которых они содержат; описываются непрерывными или ку­сочно-непрерывными функциями времени. Дискретные сигналы представляют последовательность коротких импульсов, амплитуды которых соответствуют мгновенным значениям непрерывного сиг­нала или соответствующей физической величины. Значения сигна­ла в выделенные моменты времени называются выборочными зна­чениями или отсчетами. Дискретные сигналы (дискретные во вре­мени), квантованные по уровню и представленные цифровым ко­дом, называются цифровыми сигналами. В связи с широким приме­нением цифровой обработки цифровые сигналы становятся все более распространенным видом сигналов. При анализе цифровые сигналы чаще всего заменяются дискретными, а их отличие от цифровых интерпретируется как шум.

В зависимости от ширины спектра выделяют узкополосные и широкополосные сигналы. Узкополосным называют сигнал, спектр которого сосредоточен в относительно узкой (по сравнению со средней частотой) полосе. Понятие узкополосного сигнала являет­ся довольно условным. Однако с его введением связано удобство описания и анализа сигналов.

Для передачи информации на расстояние и в ряде других слу­чаев используются высокочастотные колебания. Непосредствен­ным носителем информации, как правило, является низкочастот­ный сигнал. Перенос информации на высокочастотное, несущее колебание производится в процессе модуляции. В качестве несу­щего, кроме высокочастотного колебания, может быть использова­на также периодическая последовательность импульсов. Таким об­разом, можно выделить немодулированные и модулированные сиг­налы. Модулированные сигналы представляют несущее колебание

(гармоническое колебание или периодическую импульсную после­довательность), параметры которого изменяются под воздействием модулирующего (управляющего) сигнала. Возможна амплитудная, угловая и смешанная виды модуляции гармонического колебания. Понятие угловой модуляции объединяет два вида модуляции: фа­зовую и частотную. При модуляции импульсной последовательно­сти выделяют: амплитудную, фазовую, частотную и модуляцию длительности импульсов (широтно-импульсную модуляцию). Воз­можны смешанные виды модуляции.

В качестве модулирующего сигнала может использоваться кодо­вая последовательность различных символов. Сигнал, получаю­щийся в результате модуляции несущего колебания такой последо­вательностью, называется кодированным сигналом.

Приведенная краткая классификация сигналов не рассчитана на полноту охвата всего их разнообразия. Однако, помимо системати­зации сигналов, она позволяет уяснить и принцип выбора структуры книги.

Раздел 2.

ОБОБЩЕННЫЙ СПЕКТРАЛЬНЫЙ АНАЛИЗ СИГНАЛОВ

Спектральный анализ сигналов основан на представлении сиг­нала в виде взвешенной суммы элементарных составляющих, в математическом плане - разложении функции, описывающей сиг­нал во временной области, в ряд по системе базисных функций. Такое разложение позволяет свести анализ сложного сигнала к анализу его более простых составляющих.

При разложении сигналов чаще всего используются: система тригонометрических функций, ортогональные системы многочле­нов, в первую очередь, Лежандра, Чебышева, Лагерра, Эрмита, функций Уолша и др. При их применении для сигналов с ограни­ченной энергией обеспечивается средняя квадратичная сходимость ряда, в который раскладывается функция, описывающая сигнал.

Ортогональные системы функций полезны также при аппрокси­мации и интерполяции сигналов и их характеристик, находят при­менение при кодировании передаваемых сообщений, в вейвлетных преобразованиях и в ряде других случаев. Таким образом, анализ сигналов с использованием ортогональных систем функций имеет широкое приложение, является неотъемлемой частью общего ана­лиза сигналов. Описание ортогональных систем функций использу­ется в дальнейшем - в других разделах книги, частей 1 и 2.

В этом разделе рассматриваются наиболее распространенные ортогональные системы функций и их применение при спектраль­ном анализе сигналов.

2.1. Обобщенный ряд Фурье

Функция, описывающая сигнал во временной области s(t), мо­жет быть представлена в виде взвешенной суммы базисных функ­ций ортогональной системы {φ_n(t)}

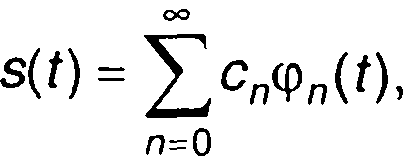(2.1)

где с_n - постоянные коэффициенты.

Такое представление сигнала означает, что сигнал рассматри­вается как совокупность элементарных колебаний, взятых с соот­ветствующими коэффициентами.

Для ортогональной на интервале [t_a, t_b] системы функций {φ_n(t)} выполняется следующее равенство

(2.2)

где ρ (t) — весовая функция; ||φ_n| - норма функций φ_n(t).

При ||φ_n|| = 1 система функций {φ_n(t} называется ортонормированной. Коэффициенты ряда (2.1) с учетом (2.2) могут быть опре­делены как

(2.3)

Ряд, в который раскладывается функция s(t), сходится в сред­нем квадратичном, если выбранная система базисных функций яв­ляется полной. Ортогональная система считается полной, если не существует никакой другой функции, не входящей в систему, кото­рая была бы ортогональна ко всем функциям данной системы.

В обобщенный ряд Фурье может быть разложена любая функ­ция, квадратично интегрируемая на интервале [t_a, t_b]. Это означает, что анализ с использованием обобщенного ряда Фурье может про­водиться для сигналов с ограниченной энергией на рассматривае­мом интервале. Разложение функции s(t) по ортогональной системе функций (2.1) называется обобщенным рядом Фурье. Совокупность коэффициентов разложения называется спектром сигнала в вы­бранной системе базисных функций.

Коэффициенты Фурье обладают следующим свойством. Любая частичная сумма ряда Фурье

(2.4)

наилучшим образом аппроксимирует функцию s(t). Это означает,

что средняя квадратичная ошибка такой аппроксимации сигнала с весом ρ (t)

(2.5)

имеет наименьшее значение по сравнению с ошибками, сопровож­дающими описание сигнала в виде (2.4) с коэффициентами, отлич­ными от (2.3). Учитывая, что σ²_N ≥ 0, из (2.5) получаем неравенство Бесселя

(2.6)

которое при N → ∞ переходит в равенство Парсеваля

(2.7)

Равенство (2.7) означает, что ряд (2.1) сходится в среднем квад­ратичном к функции s(t).

Некоторые ортогональные системы базисных функций, которые могут быть использованы при описании и анализе сигналов и их характеристик, приведены в табл. 1.3.

2.2. Спектральный анализ сигналов на основе системы тригонометрических функций

При анализе сигналов наиболее часто используется разложение временной функции, описывающей сигнал, в тригонометрический ряд Фурье (разложение по ортогональной системе тригонометриче­ских функций). Сигнал представляется в виде взвешенной суммы гармонических составляющих. Спектральный анализ, основанный на таком представлении сигналов, называется гармоническим. Ис­пользуемая система функций {cosnх, sinnх} является ортогональ­ной и полной на интервале [-π,π]. Эта система периодическая, со­храняет свою ортогональность и полноту на любом интервале дли­тельностью 2π.

Периодический сигнал s(t), имеющий частоту повторения можно представить в виде

(2.8)

где π=2π/T; Т - период сигнала.

Ортогональность базисных функций приводит к следующим ра­венствам:

(2.9)

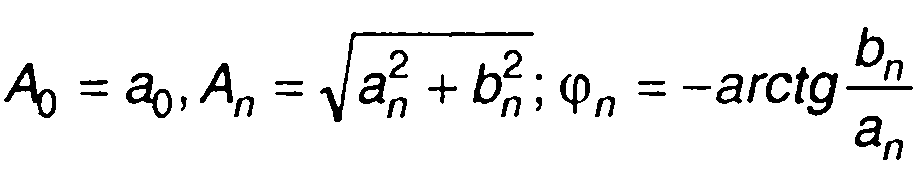
С учетом (2.9) определяются коэффициенты разложения (2.8)

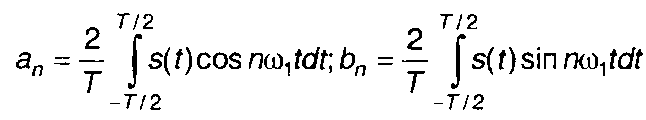(2.10)

Предполагается, что функция s(t) является квадратично интег­рируемой на интервале периодичности [- T/2, T/2]. Такие функции описывают сигналы с конечной мощностью.

От (2.8) можно перейти к несколько иной форме записи тригоно­метрического ряда Фурье

(2.11)

где

Периодический сигнал рассматривается как сумма гармониче­ских составляющих с амплитудами А_n, и начальными фазами φ_n.

Совокупность амплитуд {А_n} -амплитудный спектр, а совокупность

начальных фаз {φ_n} -фазовый спектр сигнала. Спектры сигналов

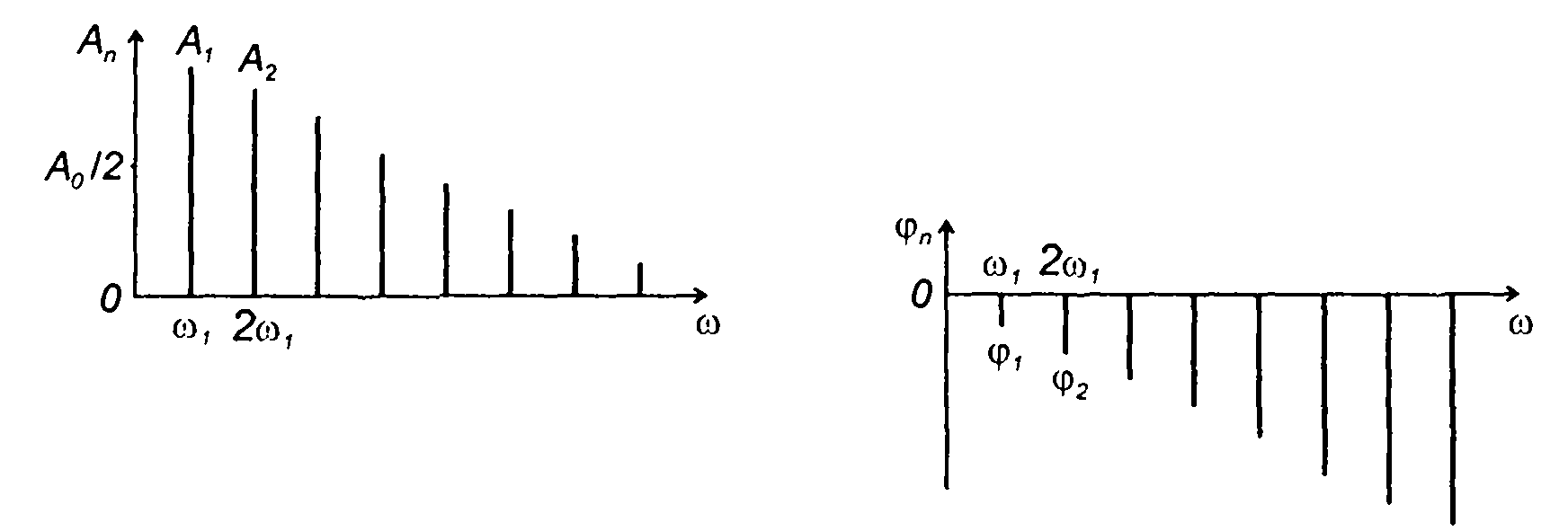
Рис. 2.1

в базисе тригонометрических функций называются частотными спектрами.

Как следует из (2.11), спектры периодических сигналов являются дискретными или линейчатыми, интервал дискретизации по частоте определяется частотой сигнала (или его периодом Т,ω₁ =2π/Т), рис. 2.1.

В качестве примера рассмотрим прямоугольное колебание (ме­андр), рис. 2.2,а. Для него из (2.10) получим

Рис. 2.2

Таким образом,

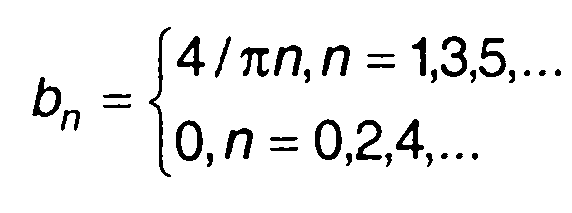
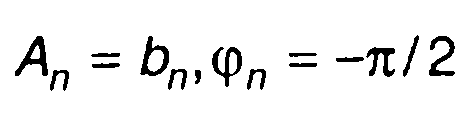
Переходя к форме записи (2.11), имеем (рис. 2.2,6)

2.3. Спектральный анализ сигналов на основе многочленов Лежандра

Система многочленов Лежандра {P_n(t)} ортогональна на интер­вале [-1, 1] с весом ρ(t) = 1. Многочлены Лежандра определяются выражением

(2.12)

Многочлены первых порядков (рис. 2.3):

P₀(t)=l,

P₁(t)=t,

P₂(t)=1/2(3t²- 1),

P₃(t)= 1/2(5t³-3t), (2.13)

P₄(t)=1/8(35t⁴-30t²+ 3),

P₅(t) = 1/8(63t⁵- 70t³+ 15t).

Условие ортогональности многочленов Лежандра записывается в виде

(2.14)

Функция s(t) раскладывается в ряд по многочленам Лежандра

(2.15)

с коэффициентами

Рис. 2.3

(2.16)

Совокупность коэффициентов (2.16) представляет спектр сигна­ла s(t) в базисе многочленов Лежандра.

В качестве примеров рассмотрим некоторые виды функций, опи­сывающих сигналы во временной области.

1. Сигнал описывается степенным многочленом

где а_n - постоянные коэффициенты.

Переходя к безразмерной величине х = 2t/τ_u, запишем

Разложим функцию в ряд по многочленам Лежандра

Приравнивая в левой и правой частях равенства коэффициенты при слагаемых с одинаковыми степенями х, получим систему урав­нений для определения коэффициентов с_n.

При N = 2; а₀ = 1; а₁ = 0; а₂ = -1, находим С₀ = 2/3; С₁ = 0; С₂ = -2/3.

Косинусоидальный импульс

Переходя к безразмерной величине х = 2f / x_u, запишем

Коэффициенты с_п определяются выражением

Вычисляя интеграл получаем

2.4. Спектральный анализ сигналов на основе многочленов Чебышева

Многочлены Чебышева первого рода определяются выражением

(2.17)

Многочлены T_n(t) первых порядков (рис. 2.4):

T₀(t) = 1,

T₁(t) = t,

T₂(t) = 2t² - 1, (2.18)

T₃(t) = 4f³ - 3f,

T₄(t) = 8t⁴ - 8t² + 1,

T₅(t) = 16t⁵ — 20t³ + 5t.

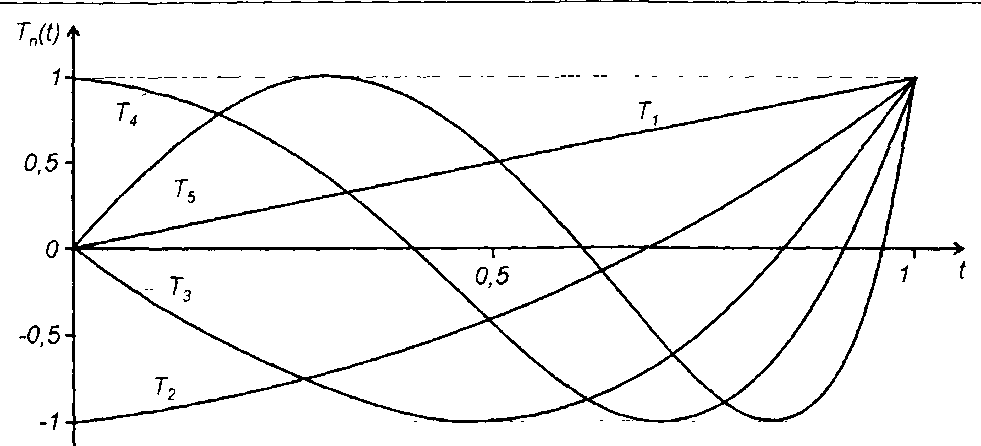
Рис. 2.4

Многочлены T_n(t) ортогональны на интервале [-1, 1] с весом

1/√(1-t²)

(2.19)

Многочлены Чебышева второго рода U_n(t) определяются через многочлены первого рода

(2.20)

Функция s(t) раскладывается в ряд по многочленам T_n(t) (2.21)

с коэффициентами

(2.22)

Совокупность коэффициентов (2.22) представляет спектр сигна­ла s(t) в базисе многочленов Чебышева.

Примеры разложения в ряд по многочленам Чебышева.

1. Функция

В ряде случаев разложение функции s(t)’no многочленам Чебы­шева на интервале [-1, 1] сводится к разложению функции s(cost) на интервале [-π, π] по косинусам. Для рассматриваемой функции используем известное соотношение

где I_n(а) - функция Бесселя.

Замена t = cosφ дает

Аналогично, из разложений по косинусам можно получить сле­дующие разложения по многочленам Чебышева.

2. Сигнал s(t) = cosπt/τ_u,│t│<τ_u/2

3. Сигнал s(t) = sin2πt/τ_u,│t│<τ_u/2.

4. Сигнал s(t) = sign2t/τ_u,│t│<τ_u/2.

5. Сигнал s(t) = 2│t│/τ_u,│t│<τ_u/2.

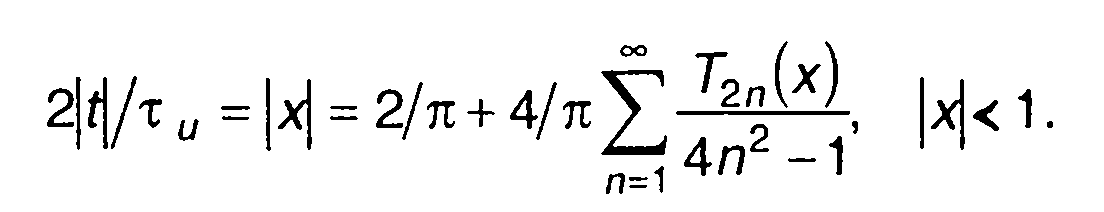
2.5. Спектральный анализ сигналов на основе многочленов Лагерра

Многочлены Лагерра L_n(T) ортогональны на полуоси [0,∞) с ве­сом ρ(t) = е^-t. Определяются выражением

(2.23)

Многочлены L_n(t) первых порядков имеют вид:

L_o(t)= 1,

L₂(t)=t²-4t+2, (2.24)

L₃(t) = t³- 9t² + 18t-6,

L₄(t)=t⁴- 16t³ + 72t²- 96t + 24,

L_s(t)= ?⁵- 25?⁴+ 200?³- 600?²+ 600t- 120.

Условие ортогональности многочленов Лагерра:

При t→∞ многочлены L_n(t) расходятся. Поэтому при разложе­нии сигналов обычно используют функции Лагерра

(2.25)

Графики Функций l_n(t) первых порядков показаны на рис. 2.5. Функции l_n(t) ортогональны и нормированы

(2.26)

Функция s(t) раскладывается в ряд по функциям Лагерра

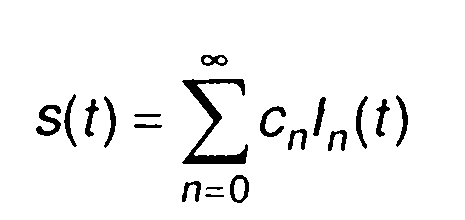(2.27)

с коэффициентами

Рис. 2.5

(2.28)

Совокупность коэффициентов (2.28) представляет спектр сигна­ла s(t) в базисе функций Лагерра.

Пример.

Сигнал описывается выражением s(t) = e^-at - e^-bt, t≥ 0.

Из (2.28) находим

2.6. Спектральный анализ сигналов на основе многочленов Эрмита

Многочлены Эрмита H_n(t) ортогональны на всей оси ( -∞,∞) с весом е ^-t. определяются выражением

(2.29)

Многочлены H_n(t) первых порядков:

H₀(t)= 1,

H₁(t) = 2t,

H₂(t) = 4t²-2, (2.30)

H₃(t) = 8t³-12t,

H₄(t)= 16t⁴-48t² + 12,

H₅(t) = 32t⁵-160t³+ 120t.

Условие ортогональности многочленов Эрмита:

(2.31)

При t→±∞ многочлены H_n(t) расходятся. Поэтому при разло­жении сигналов удобнее использовать функции Эрмита

(2.32)

Графики функций h_n(t) первых порядков показаны на рис. 2.6. Функции h_n(t) ортогональны и нормированы

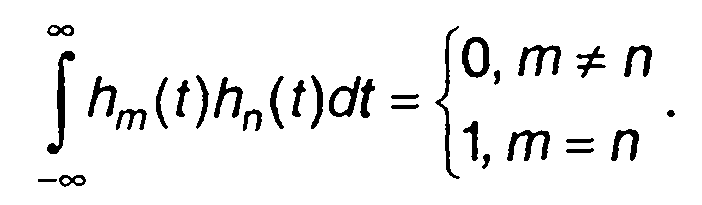
Разложение s(t) по функциям Эрмита

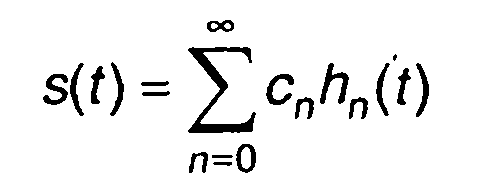(2.33)

имеет коэффициенты

(2.34)

Совокупность коэффициентов (2.34) представляет спектр сигна­ла s(t) в базисе функций Эрмита

Пример.

Сигнал - гауссов импульс s(t) = е^-at2

Рис. 2.6

Коэффициенты разложения определяются выражением

Вычисление интегралов дает

2.7. Спектральный анализ сигналов на основе функций Уолша

Спектральный анализ сигналов на основе функций Уолша нахо­дит практическое применение прежде всего при исследовании сиг­налов, формируемых в цифровых устройствах.

2.7.1. Системы функций Уолша

Функции Уолша являются кусочно-постоянными знакоперемен­ными функциями, принимающими значения 1 или -1. Они опреде­ляются с помощью функций Радемахера r_n(t) (рис. 2.13)

(2.35)

где n= 1,2,...- порядок функции; x=t/T, Т- интервал времени.

Функции Радемахера имеют вид меандра, ортонормированы. Все они являются нечетными относительно середины интервала

определения и не образуют полной системы, следовательно, не могут быть использованы при разложении функций в ряд Фурье. Ортогональная система кусочно-постоянных функций становится полной при переходе к функциям Уолша. Функции Уолша опреде­ляются произведением функций Радемахера. Принцип формирова­ния этого произведения задает систему функций Уолша. Наиболь­шее применение нашли системы функций Уолша, известные как системы Пэли, Адамара и Хармута (Уолша).

Система Пэли. Функция Уолша с номером n в системе Пэли за­дается произведением функций Радемахера с номерами к, равны­ми разрядам двоичного представления n. При двоичном представ­лении число n записывается в виде

(2.36)

где т - число разрядов.

Функции Уолша в системе Пэли определяются как

(2.37)

где п - порядок функции Уолша.

Двоичное представление n для значений от 0 до 15 приведено в табл. 2.1.

Таблица 2.1.

Двоичное представление порядка функций Уолша в системах Хармута (Уолша), Пэли и Адамара

Система Адамара. Получается из системы Пэли записью раз­рядов двоичного представления номера функции Уолша п в обрат­ном порядке

(2.38)

Комбинации n_т-k+1 соответствующие первым номерам функции Уолша, приведены в табл. 2.1.

Система Хармута. Эту систему можно получить из системы Пэ­ли, представляя номер соответствующей функции Уолша в коде Грея. Код Грея получается последовательным суммированием по модулю два соседних разрядов двоичного разложения п, начиная с младшего.

Обозначив k-ый разряд кода Грея <n_k>, запишем

(2.39)

где знак означает операцию поразрядного суммирования по мо­дулю два

Выражение для функции Уолша в системе Хармута имеет вид

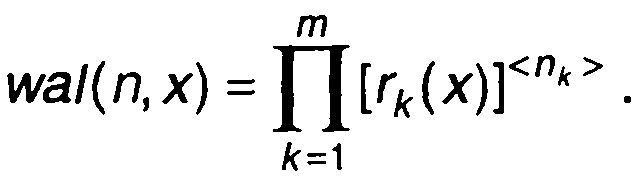(2.40)

Рис. 2.7

Комбинации <n_к>, соответствующие нумерации Функций Уолша, приведены в табл. 2.1. Определение функций Уолша первых по­рядков n < 15 в системе Хармута через функции Радемахера в со­ответствии с (2.40) дано в табл. 2.2.

Таблица 2.2.

Функции Уолша в системе Хармута (Уолша)

Графики функций Уолша, упорядоченных по Хармуту, изображе­ны на рис. 2.8. Соответствующие нумерации функций Уолша в сис­темах Пэли и Адамара приведены в двух правых столбцах на рис. 2.8. Из графиков функций Уолша, приведенных на рисунке, видно, что порядковый номер функции в системе Хармута равен числу пересечений ее графика с осью абсцисс на интервале [0, 1]. Поэтому нумерация функций Уолша по Хармуту называется также упорядочением по частоте.

В системе Хармута четные относительно середины интервала функции чередуются с нечетными. Эти функции имеют соответст­венно четные и нечетные номера. В этом функции Уолша в системе Хармута подобны тригонометрическим функциям и их по аналогии иногда обозначают:

четные саl(n,х) = wal(n,x), n = 2k,

нечетные sal(n,x) = wal(n,x), n = 2k+1.

Рассмотренные системы содержат одни и те же функции Уолша, только расположенные в различной последовательности.

2.7.2. Свойства функций Уолша

Из свойств функций Уолша, определенных на интервале [0, 1], отметим следующие.

1. Функции Уолша являются периодическими с периодом, рав­ным единице

(2.41)

2. Модуль функции Уолша равен единице, среднее значение для n≠0 равно нулю

(2.42)

Рис. 2.8

3. Функции Уолша ортонормировании на интервале [0, 1]

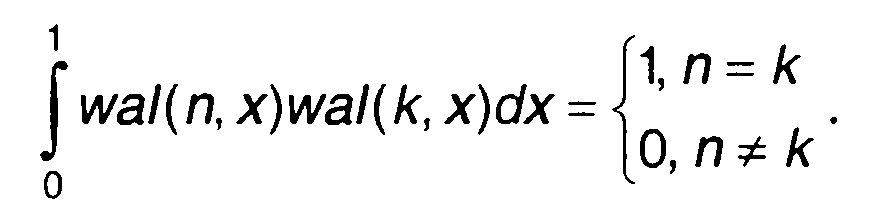(2.43)

4. Произведение двух функций Уолша является также функцией Уолша

(2.44)

Для систем Пэли и Адамара

(2.45)

для системы Хармута

(2.46)

где символ <^----------> означает преобразование кода Грея в двоич­ный код.

5. Параметры n и х симметричны: любые выводы относительно п справедливы для х и наоборот.

Такой вывод следует непосредственно из выражений (2.37), (2.38) и (2.40).

2.7.3. Спектры сигналов в базисе Уолша

Сигнал, описываемый интегрируемой функцией s(t) и опреде­ленный на интервале [0, Т], можно разложить в обобщенный ряд Фурье по функциям Уолша

(2.47)

где

Совокупность коэффициентов с_п представляет спектр сигнала в базисе Уолша или спектр Уолша. При вычислении спектров Уолша выражение для с_п целесообразно представить несколько в иной форме. Разобьем интервал значений t/T на N участков, в пределах которых функция wal(n,t/T) постоянна. С учетом этого выражение для с_п запишем в виде