ДЕТЕРМИНИРОВАННЫЕ СИГНАЛЫ 3 страница

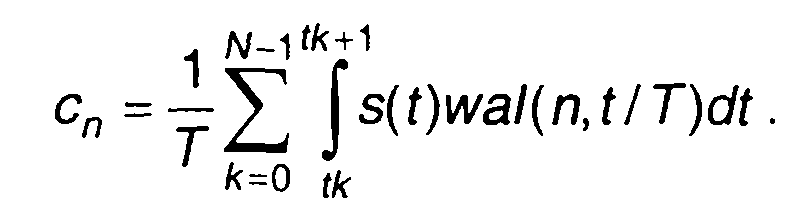(2.48)

Из (2.48) получим

(2.49)

С учетом того, что функции Уолша равны ±1, выражение (2.49) запишем в виде

(2.50)

где а_п(к) = 0 или 1, определяет знак функции Уолша на интервале Примеры спектров Уолша.

1. Спектр Уолша прямоугольного импульса s(t) = 1, 0 ≤ t ≤ т (рис. 2.9)

Из (2.50) находим

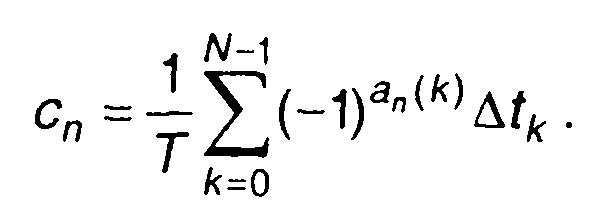
Спектр Уолша прямоугольного импульса зависит от соотноше­ния между т и Т. При τ/T = 2^v где v - целое положительное число, с учетом значений функций Уолша получим

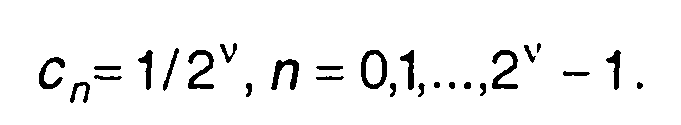
Разложение прямоугольного импульса по функциям Уолша име­ет вид

Спектр состоит из 2^V составляющих с одинаковыми амплитуда­ми, равными 1/2^V. Спектр содержит конечное число составляющих. При т/Т≠ 2^V структура спектра изменится.

Рис.2.9

2. Спектр Уолша треугольного импульса (рис. 2.10) При описании треугольного импульса

удобно перейти к безразмерному времени х= t/T

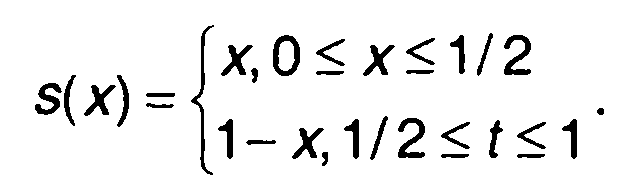
В соответствии с (2.50) находим:

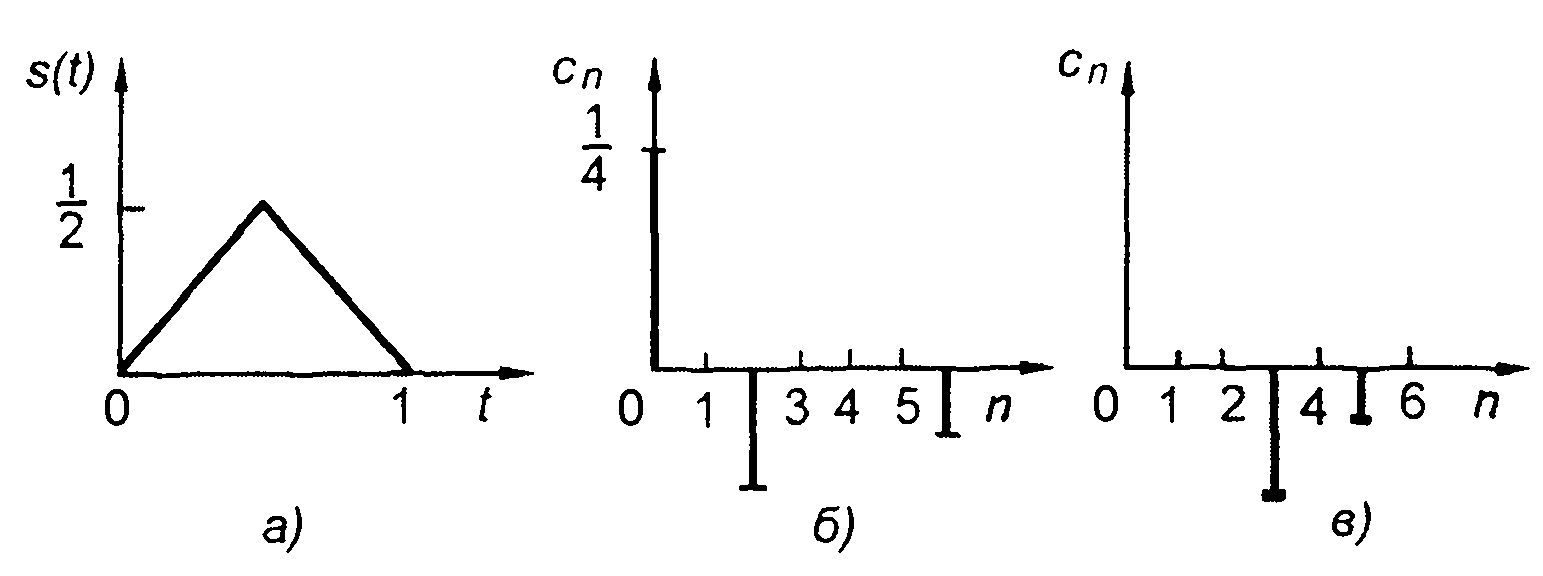
Рис. 2.10

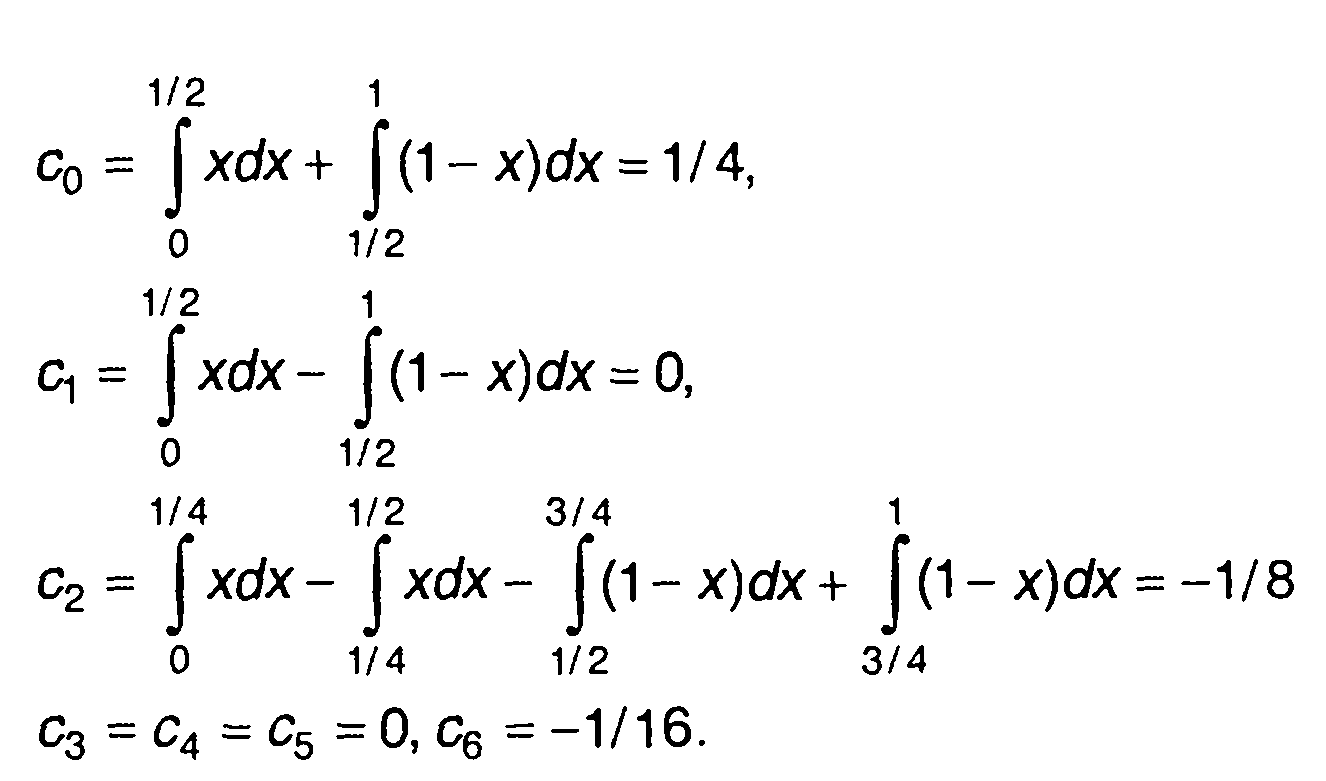
Спектры Уолша при нумерации Хармута и Пэли изображены на рис.2.10, б и в.

3. Спектр Уолша синусоидального импульса (рис. 2.11)

Для синусоидального импульса

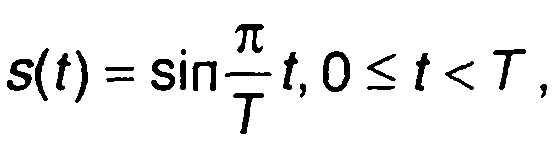
переходя к безразмерному времени x = t/T, запишем

Из (2.50) в системе Хармута находим (рис. 2.11):

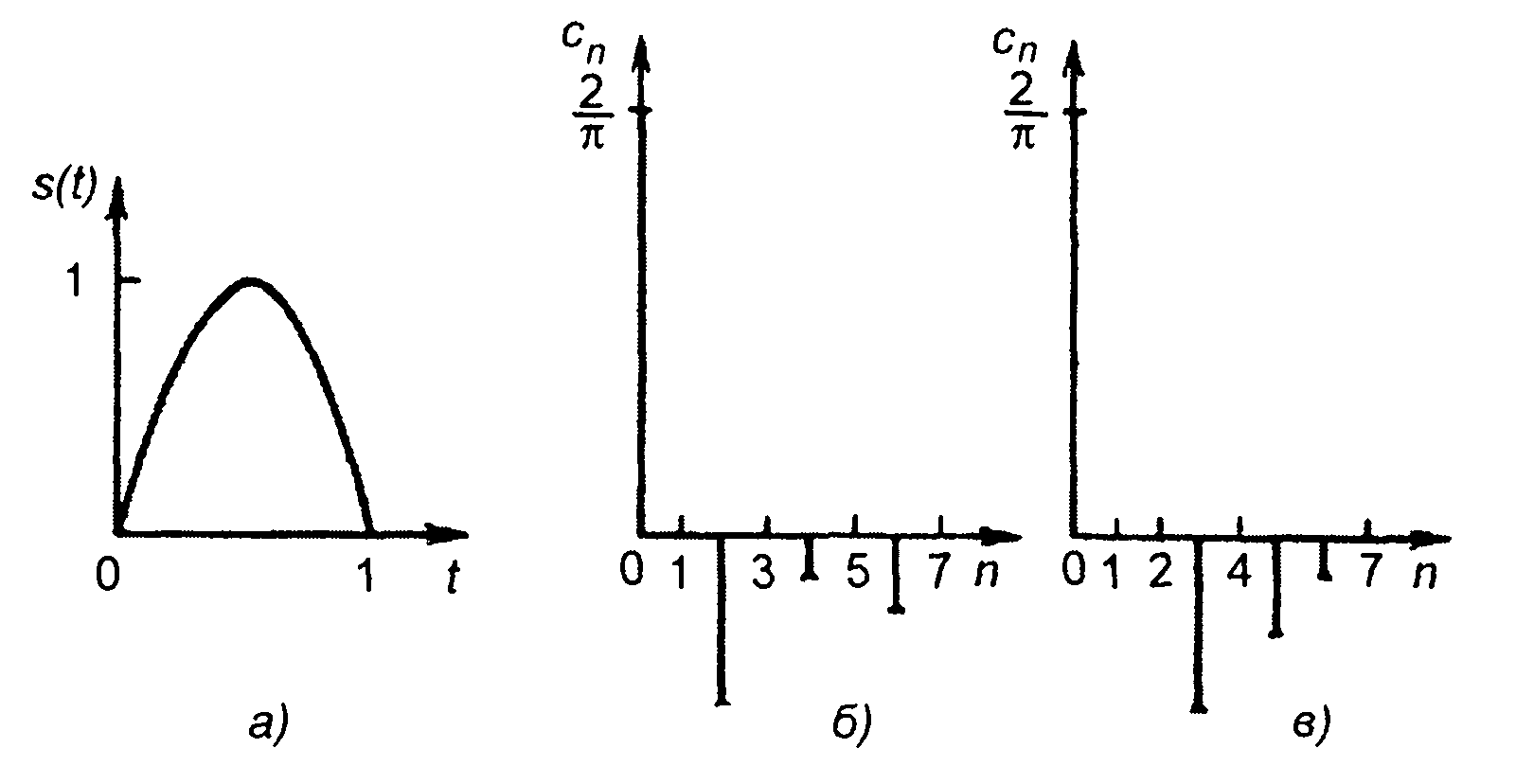
Рис. 2.11

Спектры Уолша рассматриваемого сигнала при нумерации Хар­мута и Пэли приведены на рис.2.11,6 и в.

2.7А. Свойства спектров Уолша

При анализе сигналов с использованием функций Уолша полез­но учитывать свойства разложения сигналов в базисе Уолша - спектров Уолша.

1. Спектр суммы сигналов равен сумме спектров каждого из сиг­налов.

Спектр сигнала в системе функций Уолша определяется коэф­фициентами разложения (2.47). Для суммы сигналов коэффициен­ты разложения определяются выражением

(2.52)

где а_пк- коэффициенты разложения сигнала s_k(t).

2. Умножение сигнала на функцию Уолша с номером n изменяет номера коэффициентов разложения с_k по закону двоичного сдвига по модулю два

(2.53)

3. Спектр Уолша произведения сигналов s₁(t) и s₂(t). определен­ных на интервале [0, T) и имеющих спектры с¹_к,с²_к, равен

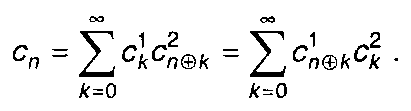(2.54)

4. Свертку сигналов s₁(t) и s₂(t)

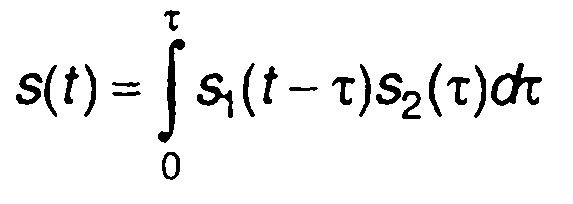(2.55)

можно представить в виде

(2.56)

где с¹_к,с²_к,- спектры Уолша сигналов s₁(t) и s₂(t).

Рассмотренные разложения по ортогональным системам при­менимы к любым функциям, удовлетворяющим некоторым услови­ям, сформулированным ранее. Они могут использоваться как при анализе сигналов, так и их характеристик. Ряды с ограниченным числом членов могут рассматриваться как аппроксимирующие. Ко­эффициенты разложения, определенные как коэффициенты Фурье, обеспечивают оптимальность такой аппроксимации.

ГАРМОНИЧЕСКИЙ АНАЛИЗ СИГНАЛОВ

В основе гармонического анализа детерминированных сигналов лежит представление временной функции, описывающей сигнал, в виде тригонометрического ряда Фурье или ее интегральное преоб­разование Фурье - сигнал рассматривается как бесконечная или конечная совокупность гармонических составляющих. В радиотех­нике из всех видов спектрального анализа сигналов гармонический анализ получил почти исключительное применение. Поэтому поня­тия спектральный и гармонический анализ часто имеют одно со­держание. Широкое применение гармонического анализа при опи­сании сигналов объясняется рядом причин, главные из которых связаны с распространением гармонических колебаний в природе и простотой аппаратурной реализации методов их анализа.

3.1. Гармонический анализ периодических сигналов

Гармонический анализ периодических сигналов основан на раз­ложении временной функции s(t), описывающей сигнал с периодом Т и частотой ω₁ = 2π/Т, по ортогональной системе тригонометри­ческих функций {cosnω₁t, sinnω₁t} Для периодической функции s(t) тригонометрический ряд Фурье имеет вид

(3.1)

Коэффициенты ряда определяются выражениями

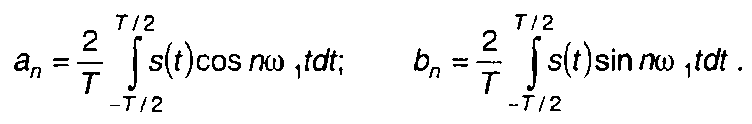(3.2)

Функция s(t) должна быть квадратично интегрируемой на ин­тервале периодичности [-T/2, T/2]. Такие функции описывают пе­риодические сигналы с ограниченной мощностью.

Для четной функции s(t), как это следует из (3.2),

(3.3)

для нечетной функции s(t):

(3.4)

Обычно при анализе сигналов используется разложение s(t) в виде

(3.5)

где

(3.6)

Периодический сигнал представляется в виде суммы гармони­ческих составляющих с амплитудами А_n и начальными фазами.

Совокупность амплитуд {Д,} определяет амплитудный спектр, а совокупность начальных фаз {φ_n} - фазовый спектр сигнала (рис.3.1,а). Как следует из (3.5), спектры периодических сигналов являются дискретными или линейчатыми, интервал дискретизации по частоте равен частоте сигнала ω₁ = 2π/ Т.

Тригонометрический ряд Фурье можно записать в комплексной форме

(3.7)

где

(3.8)

Переход от (3.1) к (3.7) очевиден с учетом формулы Эйлера

(3.9)

Рис.3.1

Коэффициенты с_n в общем случае являются комплексными ве­личинами

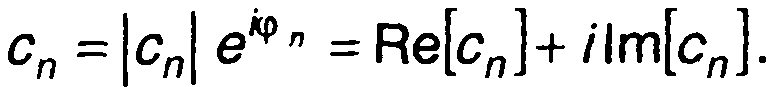(З.10)

При использовании комплексной формы ряда Фурье сигнал оп­ределяется совокупностью комплексных амплитуд {с_n}. Модули комплексных амплитуд |с_n| описывают амплитудный спектр, аргу­менты φ_n - фазовый спектр сигнала (рис. 3.1,6).

Представив (3.8) в виде

(3.11)

Как следует из записанных выражений, амплитудный спектр об­ладает четной, а фазовый - нечетной симметрией

получим

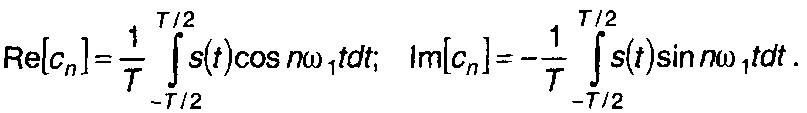(3.12)

(3.13)

Из сопоставления выражений (3.2) и (3.11) следует

(3.14)

В качестве примера рассмотрим периодическую последователь­ность прямоугольных импульсов (рис. 3.2,а). При разложении пе­риодической последовательности прямоугольных импульсов в три­гонометрический ряд Фурье из (3.2) получим амплитудный и фазо­вый спектры в виде (рис.3.2,б):

При использовании комплексной формы ряда Фурье из (3.8) следует:

Амплитудный и фазовый спектры сигнала равны

Предельным видом ряда Фурье является интеграл Фурье. Пе­риодический сигнал при Т → ∞ становится непериодическим. Под­ставив (3.8) в (3.7), запишем

(3.16)

Гармонический анализ сигналов

Рис. 3.2

Преобразуя (3.16), при T→∞ (в этом случае ω₁→ dω и пω₁ = ω), получаем

(3.17)

В квадратных скобках записан интеграл Фурье, он описывает спектральную плотность сигнала

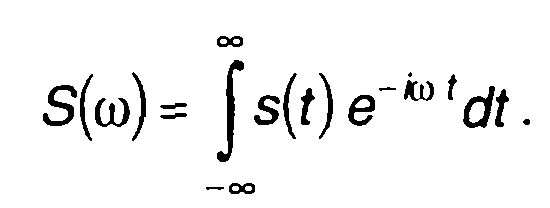
Выражение (3.17) примет вид

Записанные соотношения представляют прямое и обратное преобразования Фурье. Они используются при гармоническом ана­лизе непериодических сигналов.

3.2. Гармонический анализ непериодических сигналов

Прямое и обратное преобразования Фурье устанавливают вза­имно однозначное соответствие между сигналом (временной функ­цией, описывающей сигнал s(t) ) и его спектральной плотностью S(ω):

(3.18)

Соответствие по Фурье обозначим:

(3.19)

Условием существования преобразования Фурье является аб­солютная интегрируемость функции s(t)

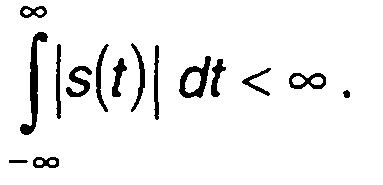(3.20)

В практических приложениях более удобным является условие интегрируемости квадрата этой функции

(3.21)

Для реальных сигналов условие (3.21) эквивалентно условию (3.20), но имеет более очевидный физический смысл: условие (3.21) означает ограниченную энергию сигнала. Таким образом, можем считать возможным применение преобразования Фурье к сигналам с ограниченной энергией. Это непериодические (импульс­ные) сигналы. Для периодических сигналов разложение на гармо­

нические составляющие производится с помощью ряда Фурье.

Функция S(ω) в общем случае является комплексной

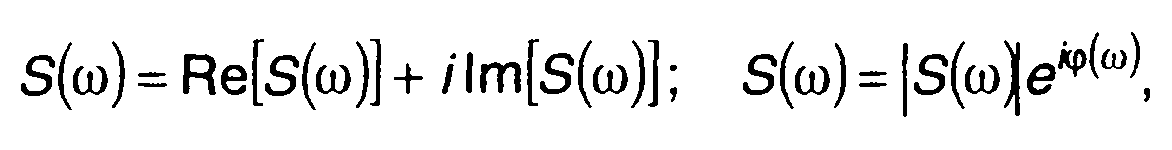(3.22)

где Re, lm - действительная и мнимая части комплексной величины; |s(w)|, ф(оо)- модуль и аргумент комплексной величины:

Модуль спектральной плотности сигнала |S(ω)| описывает рас­пределение амплитуд гармонических составляющих по частоте, на­зывается амплитудным спектром. Аргумент φ(ω) дает распределе­ние фазы по частоте, называется фазовым спектром сигнала. Ам­плитудный спектр является четной функцией, а фазовый спектр - нечетной функцией частоты

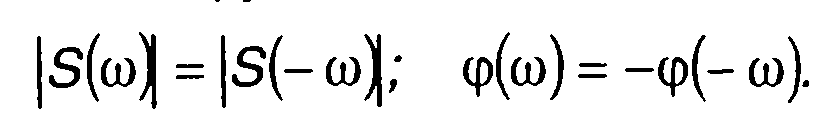(3.23)

С учетом формулы Эйлера (3.9) выражение для S(ω) запишем в виде

(3.24)

Если s(t)четная функция, то из (3.24) получим

(3.25)

Функция S(ω), как следует из (3.25), является действительной функцией. Фазовый спектр определяется как

(3.26)

Для нечетной функции s(t) из (3.24) получим

(3.27)

Функция S(ω) является чисто мнимой, фазовый спектр

(3.28)

Любой сигнал можно представить как сумму четной s_ч(t) и нечет­ной s_H(t) составляющих

(3.29)

Возможность такого представления становится ясной с учетом следующих равенств:

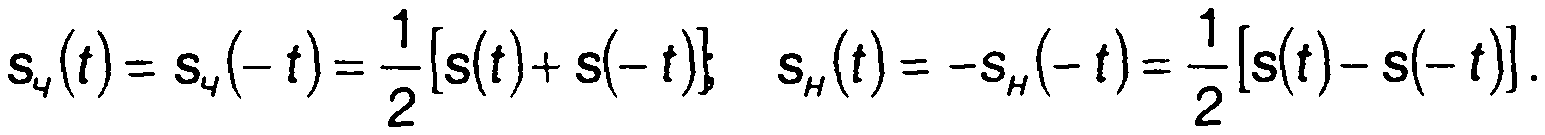
Из (3.24) и (3.29) получим

(3.30)

Следовательно, для действительной и мнимой частей спек­тральной плотности сигнала можно записать:

Таким образом, действительная часть спектральной плотности представляет преобразование Фурье от четной составляющей, мнимая часть - от нечетной составляющей сигнала. Действитель­ная часть комплексной спектральной плотности сигнала является четной, а мнимая часть - нечетной функцией частоты.

Спектральная плотность сигнала при ω = 0

(3.31)

равна площади под кривой s(t).

В качестве примеров получим спектры некоторых сигналов.

1. Прямоугольный импульс (рис. 3.3,а)

Рис. 3.3

где τ_и - длительность импульса.

Спектральная плотность сигнала

Графики амплитудного и фазового спектров сигнала приведены на рис. 3.3,б,в.

2. Сигнал, описываемый функцией

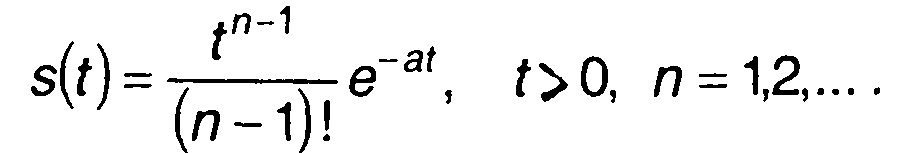
Спектральная плотность сигнала определяется выражением

Интегрируя по частям n-1 раз, получаем

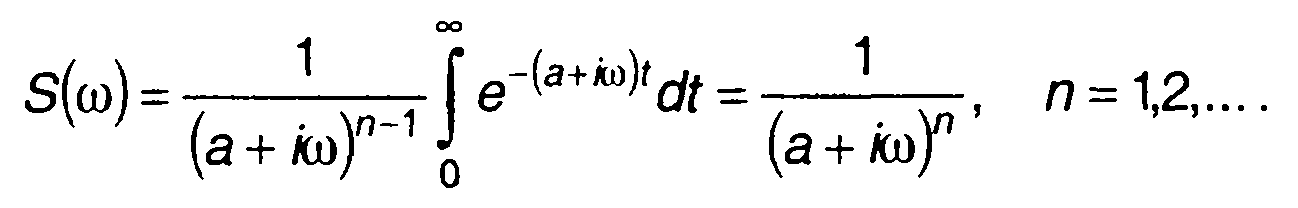
Сигнал (рис. 3.4,а)

имеет спектральную плотность

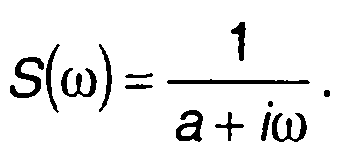
Графики амплитудного и фазового спектров изображены на рис. 3.4,б,в.

Сигнал (рис. 3.5,а)

имеет спектральную плотность

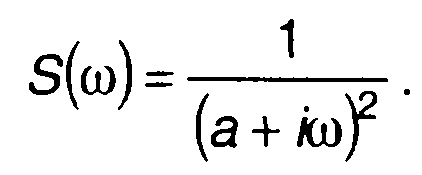
Графики амплитудного и фазового спектров - рис. 3.5,б,в.

Число примеров увеличивает табл. 3.1.

Сравнение (3.18) и (3.8) показывает, что спектральная плотность одиночного импульса при τ<<T отличается от коэффициентов ряда Фурье периодической последовательности импульсов только мно­жителем 1/T.

Рис.3.4.

С учетом указанного соотношения определение спектра периоди­ческого сигнала в ряде случаев можно упростить, используя преобра­зование Фурье (3.18). Коэффициенты ряда Фурье находятся как

(3.32)

где S(ω) - спектральная плотность одного импульса.

Таким образом, при определении амплитудного и фазового спектров периодических сигналов полезно иметь в виду следующие равенства:

(3.33)

Рис. 3.5

Коэффициент 1/T может рассматриваться как интервал частот между соседними составляющими спектра, а спектральная плот­ность как отношение амплитуды составляющей сигнала к интерва­лу частот, которому соответствует амплитуда. С учетом этого ста­новится более понятным термин «спектральная плотность». Не­прерывные амплитудный и фазовый спектры одиночного импульса являются огибающими дискретных амплитудного и фазового спек­тров периодической последовательности таких импульсов.

С помощью соотношений (3.33) результаты, приведенные в табл. 3.1, можно использовать для определения спектров перио­дических последовательностей импульсов. Такой подход иллюст­рируют следующие примеры.

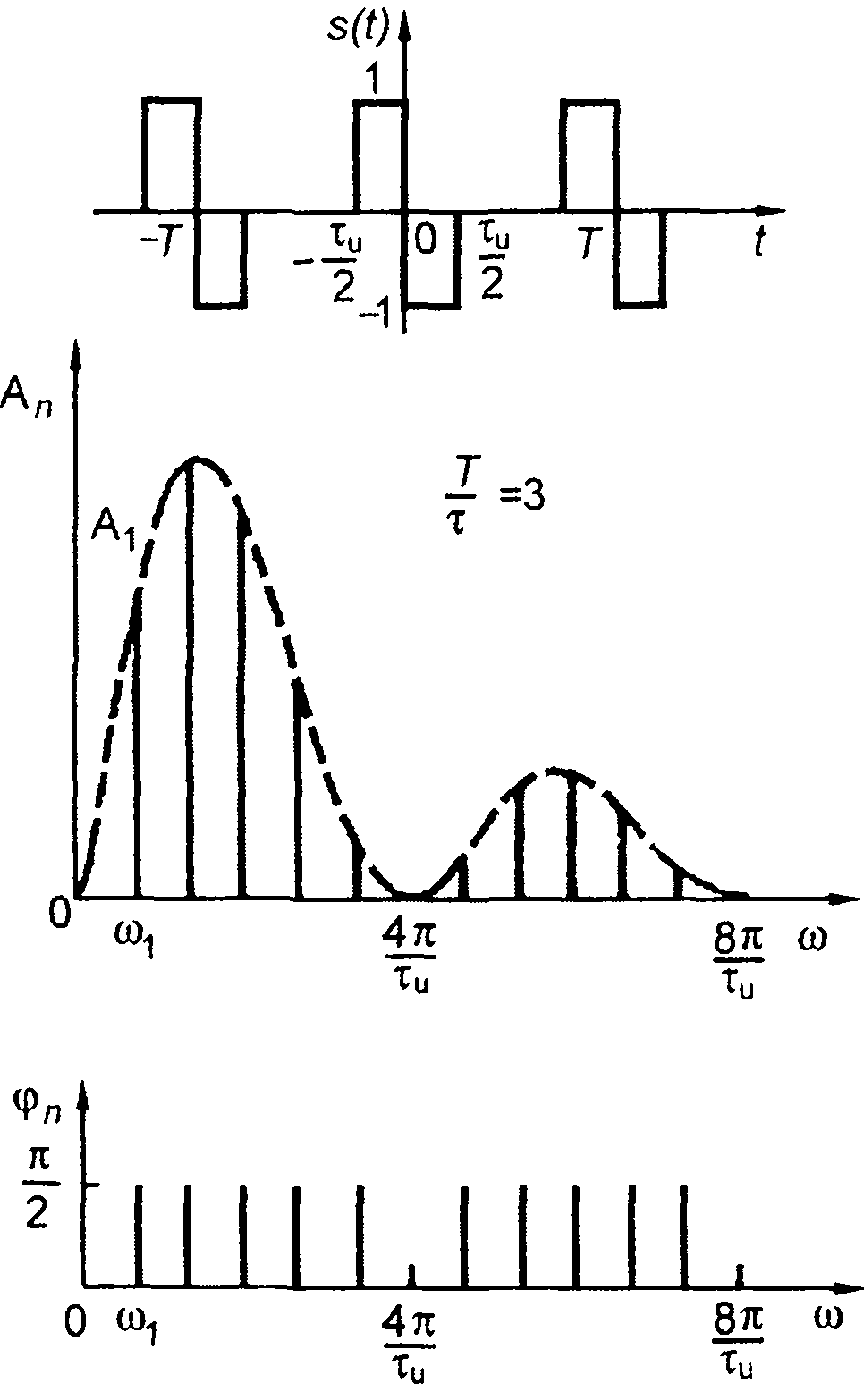
Рис.3.6

1. Периодическая последовательность прямоугольных им­пульсов (табл. 3.1, п. 1), рис. 3.2.

Записанное выражение повторяет результат примера п.3.1.

2. Периодическая последовательность меандровых импульсов (табл. 3.1, п.2), рис. 3.6, рис. 3.2.

3. Периодическая последовательность экспоненциальных импульсов (табл. 3.1, п.8), рис. 3.7.

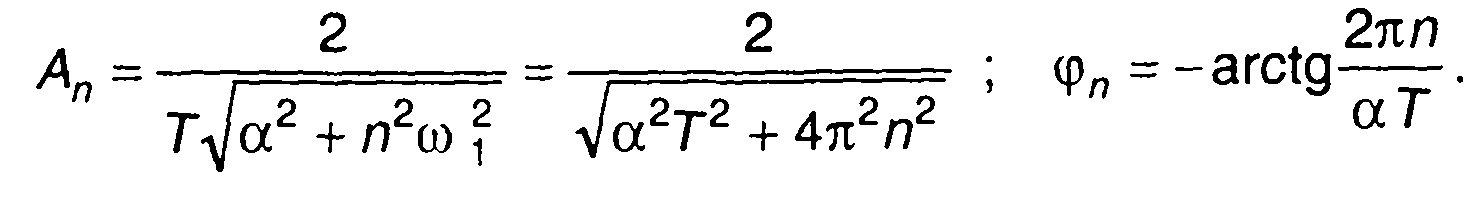
Рис. 3.7

Таблица 3.1

Сигналы и их спектры

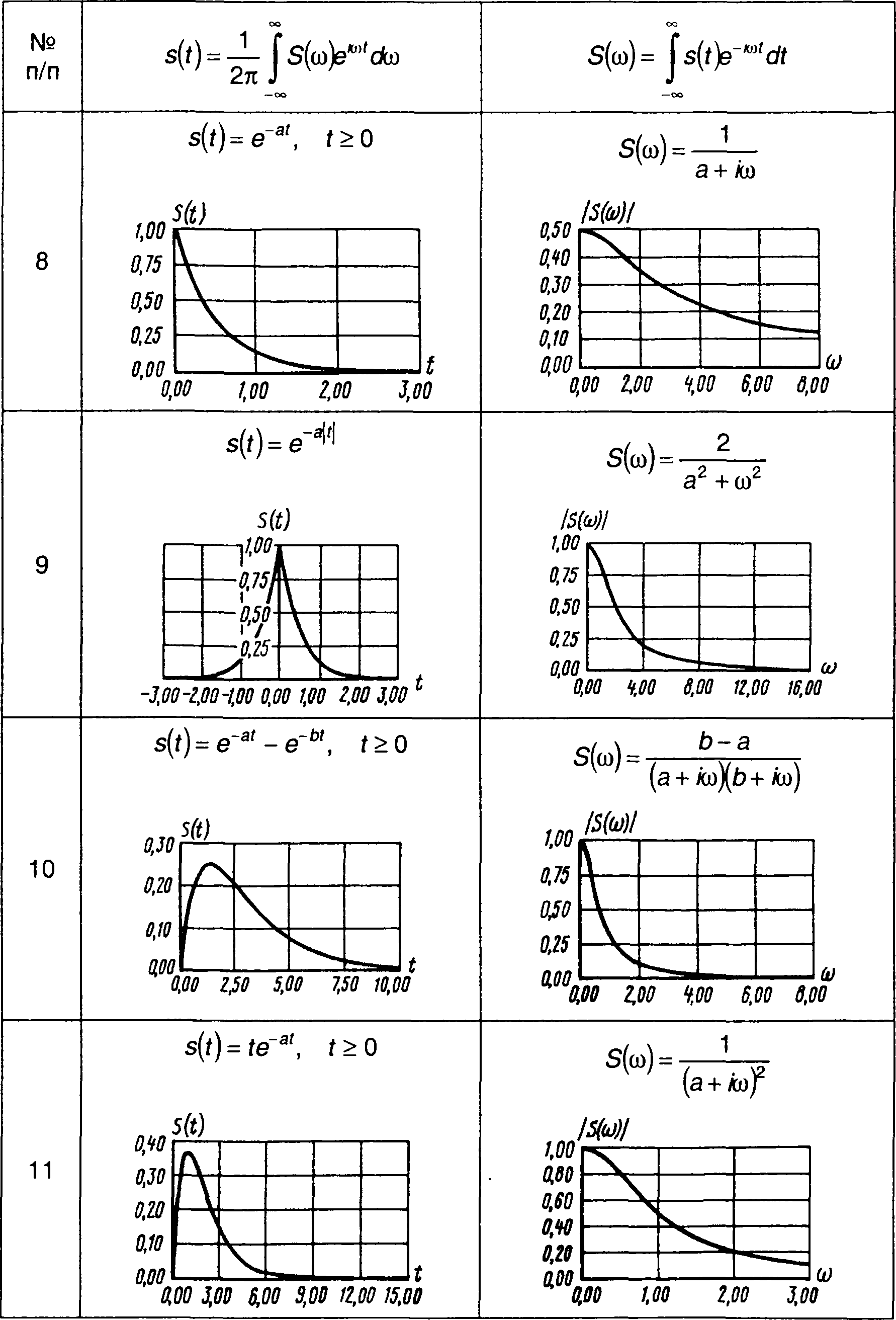
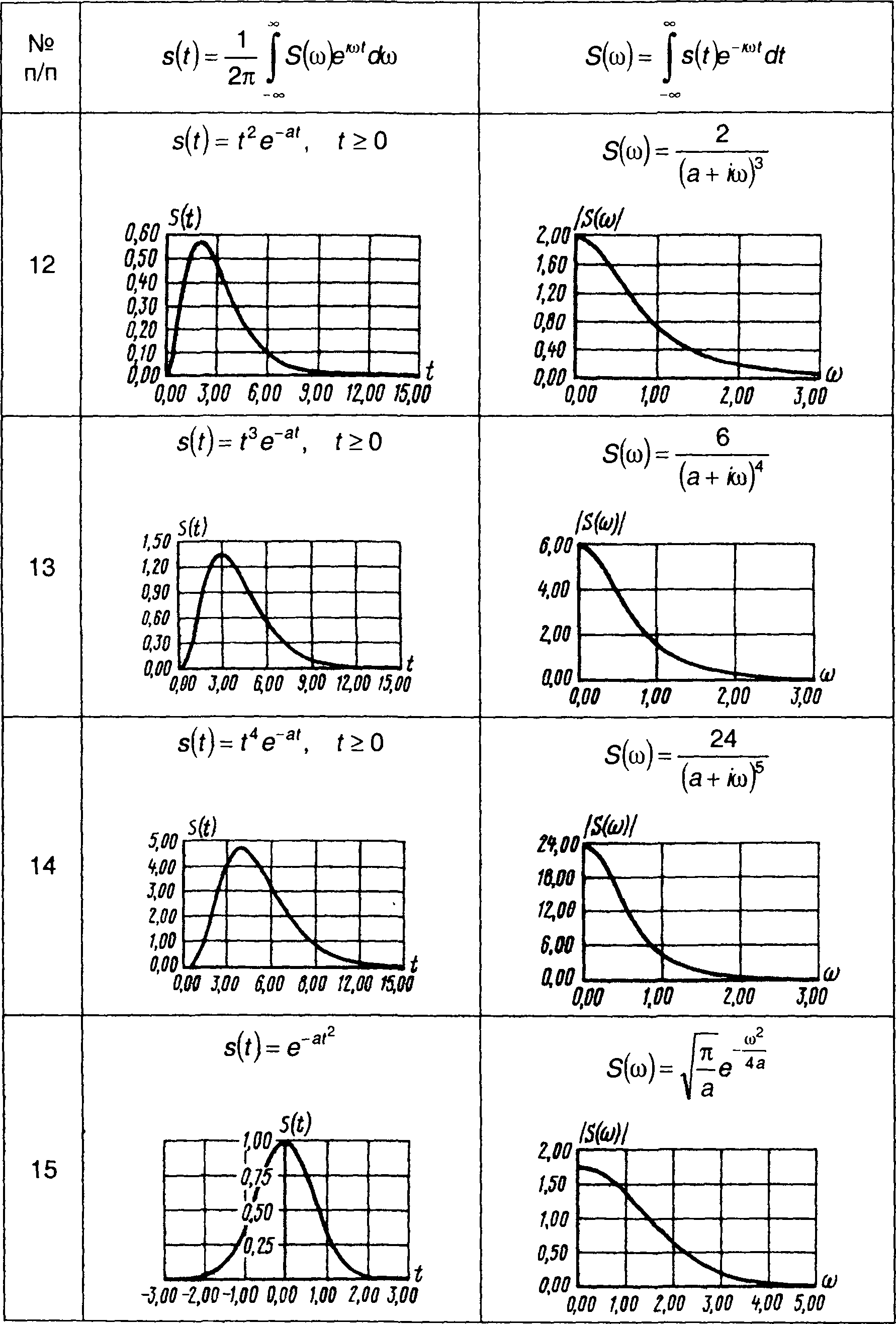
3.3. Частотные спектры сигналов, представленных в виде обобщенного ряда Фурье

При представлении сигнала в виде обобщенного ряда Фурье полезно иметь преобразование Фурье базисных функций. Это по­зволит от спектра в базисе различных ортогональных систем пе­рейти к частотному спектру. Ниже приведены примеры частотных спектров некоторых видов сигналов, описываемых базисными функциями ортогональных систем.

1 .Сигналы Лежандра.

Преобразование Фурье многочлена Лежандра (разд. 2) имеет вид

(3.34)

Где

п= 1,2, ... - многочлен Лежандра; - функция Бесселя.

Используя (3.34), от сигнала, представленного в виде ряда

с коэффициентами

можно перейти к спектральной плотности сигнала

(3.35)

Выражение (3.35) описывает спектральную плотность сигнала s(f) в виде ряда.

Графики составляющих спектра с номерами 1 - 3 приведены на рис.3.8.

2. Сигналы Лагерра.

Преобразование Фурье функции Лагерра имеет вид

(3.36)

где

п= 1,2,...- функции Лагерра.

Используя (3.36), от сигнала, представленного в виде ряда раз­ложения по многочленам Лагерра (разд. 2)

с коэффициентами

можно перейти к спектральной плотности сигнала

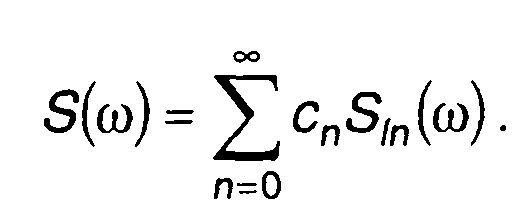(3.37)

Рис.3.8

3. Сигналы Эрмита.

Преобразование Фурье функции Эрмита имеет вид

(3.38)

где

п= 1,2,...- функции Эрмита.

Из (3.38) следует, что функции Эрмита обладают свойством трансформируемости, т.е. функции и их преобразования Фурье равны (с точностью до постоянных коэффициентов). Используя (3.38), от сигнала, представленного в виде ряда разложения по многочленам Эрмита

с коэффициентами

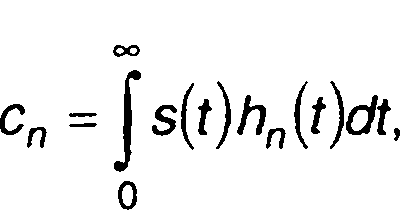
можно перейти к спектральной плотности сигнала

(3.39)

4. Сигналы Уолша.

Частотные спектры сигналов Уолша (сигналов, описываемых функциями Уолша) определяются следующим преобразованием Фурье:

(3.40)

где wal(n,x) - функция Уолша.

Так как функции Уолша имеют N участков постоянных значений,

то

(3.41)

где х_к - значение х на к-ом интервале.

Из (3.41) получим

(3.42)

где

Так как функции Уолша принимают значения ±1, то (3.42) можем записать в виде

(3.43)

где а _n(к) = 0 или 1 определяет знак функции wal(n,x_k).

На рис. 3.9 приведены графики амплитудных спектров первых шести сигналов Уолша.

3.4. Спектры сигналов, описываемых неинтегрируемыми функциями

Преобразование Фурье существует только для сигналов с ко­нечной энергией (для которых выполняется условие (3.21)). Расши­рить класс сигналов, анализируемых с использованием преобразо­вания Фурье, позволяет чисто формальный прием, основанный на введении понятия спектральной плотности для импульсной функ­ции. Рассмотрим некоторые из таких сигналов.

1. Импульсная функция.

Импульсная функция (или δ - функция) определяется как

(3.44)

Из определения импульсной функции следует ее фильтрующее свойство

(3.45)

Спектральную плотность импульсной функции определим как

(3.46)

Рис.3.9

Амплитудный спектр равен единице, фазовый спектр φ(ω) = ωt₀ (рис. 3.10).

Обратное преобразование Фурье дает

(3.47)

Рис. 3.10

По аналогии с (3.47) для частотной области запишем

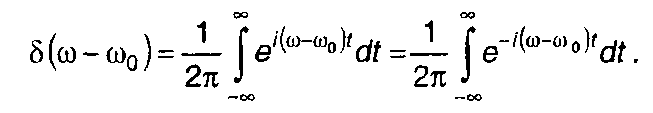(3.48)

Используя полученные выражения, определим спектральные плотности некоторых видов сигналов, описываемых функциями, для которых не существует преобразования Фурье.

2. Постоянный сигнал s(t) = s₀.

С учетом (3.48) получим (рис. 3.11)

(3.49)

3. Гармонический сигнал.

(3.50)

Спектральная плотность сигнала получится с учетом (3.48) в виде

Рис. 3.11

(3-51)

При φ = 0 (рис. 3.12)

(3.52)

Для сигнала

(3.53)

по аналогии с (3.52) найдем

(3.54)

4. Единичная ступенчатая функция.

(3.55)

Единичную ступенчатую функцию σ(t) будем рассматривать как предельный вид экспоненциального импульса

Экспоненциальный импульс представим в виде суммы четной и нечетной составляющих (3.29)

(3.56)

При a → 0

s_ч(t) =1/2 для всех значений t,

(3.57)

Рис. 3.12

Действительная часть спектральной плотности соответствует четной составляющей сигнала, мнимая часть - нечетной состав­ляющей. Переходя к пределу при а → 0, получим

(3.58)

Таким образом,

(3.59)

где <-> - символ соответствия по Фурье.

Спектральные плотности некоторых сигналов, описываемых неинтегрируемыми функциями из наиболее часто встречающихся на практике, приведены в табл. 3.2.