ДЕТЕРМИНИРОВАННЫЕ СИГНАЛЫ 6 страница

называется выборочной функцией (рис. 6.2,а). Ее как периодиче­скую функцию можно представить в виде ряда Фурье

(6.3)

Спектральная плотность выборочной функции определяется преобразованием Фурье (6.3)

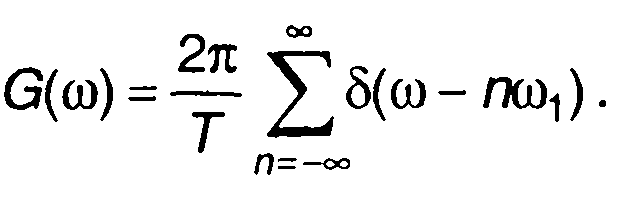(6.4)

Таблица 6.1

Дискретные сигналы

Как следует из (6.4), периодической последовательности им­пульсных функций на временной оси соответствует периодическая последовательность импульсных функций на оси частот (рис. 6.2,6).

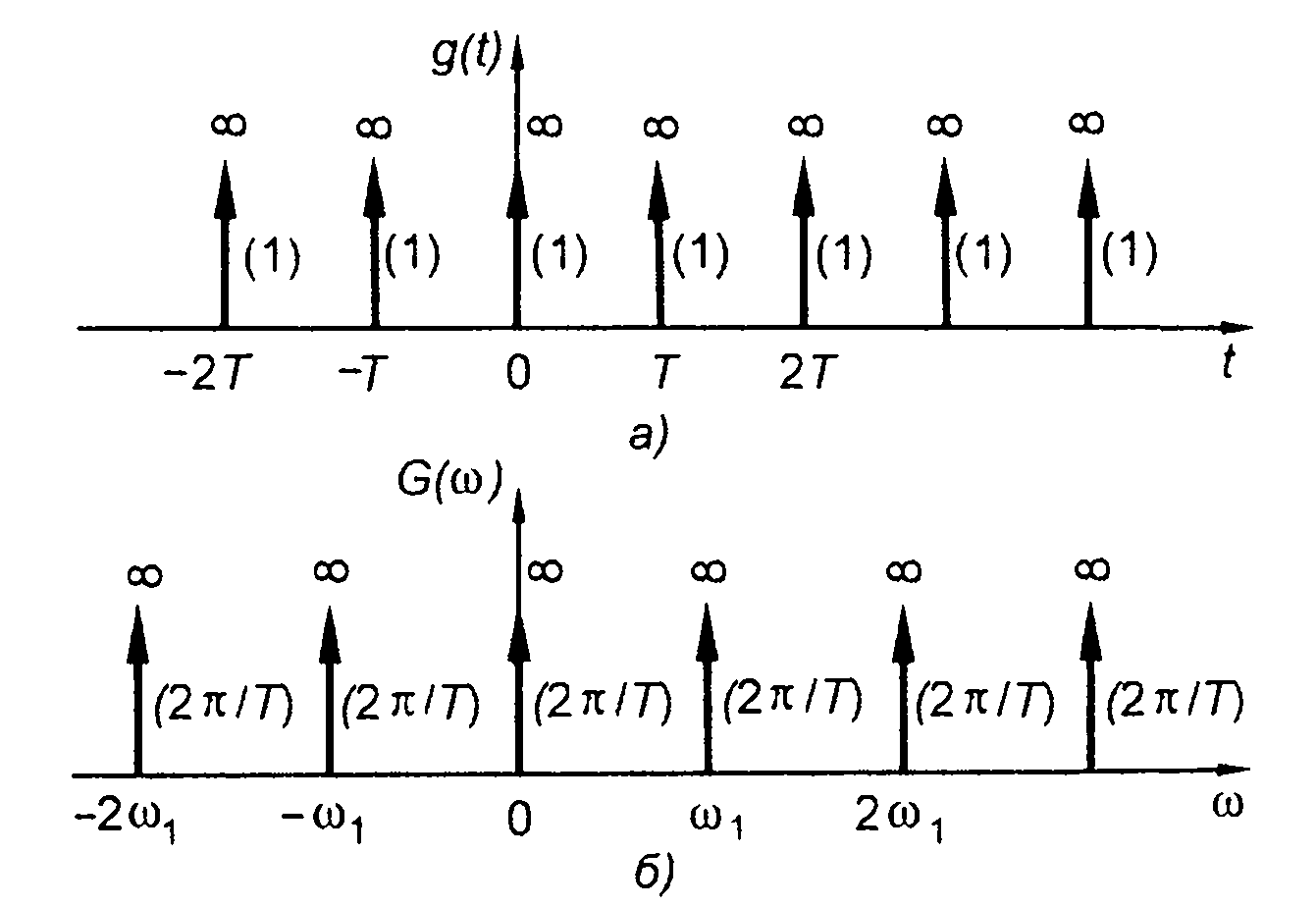
Рис. 6.2

Используя свойства преобразования Фурье, из (6.1) получим спектральную плотность дискретного сигнала s_g(t). Она определя­ется с учетом (6.1) как свертка спектральных плотностей сигналов s(t) и g(t) под знаком суммы

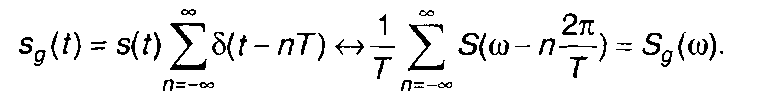(6.5)

Как показывает (6.5), спектр дискретного сигнала - периодиче­ский, бесконечный, получается периодическим повторением спек­тра исходного сигнала (с коэффициентом 1/Т) на оси частот с ин­тервалом ω₁ = 2π/Т (рис. 6.3,6).

При описании дискретного сигнала стробирующий сигнал в (6.1) рассматривается как последовательность бесконечно узких им­пульсов, описываемых δ-функцией. На практике же этот сигнал представляет последовательность импульсов конечной длительно­сти. Периодическая последовательность видеоимпульсов, полу­чающаяся при формировании выборки из непрерывного сигнала, в этом случае может быть описана как (рис. 6.4,а)

s_g(t) = s(t)u(t), (6.6)

где s(t) - непрерывный сигнал; u(t) - периодическая последова­тельность прямоугольных импульсов единичной амплитуды, дли­тельности т, с периодом Т.

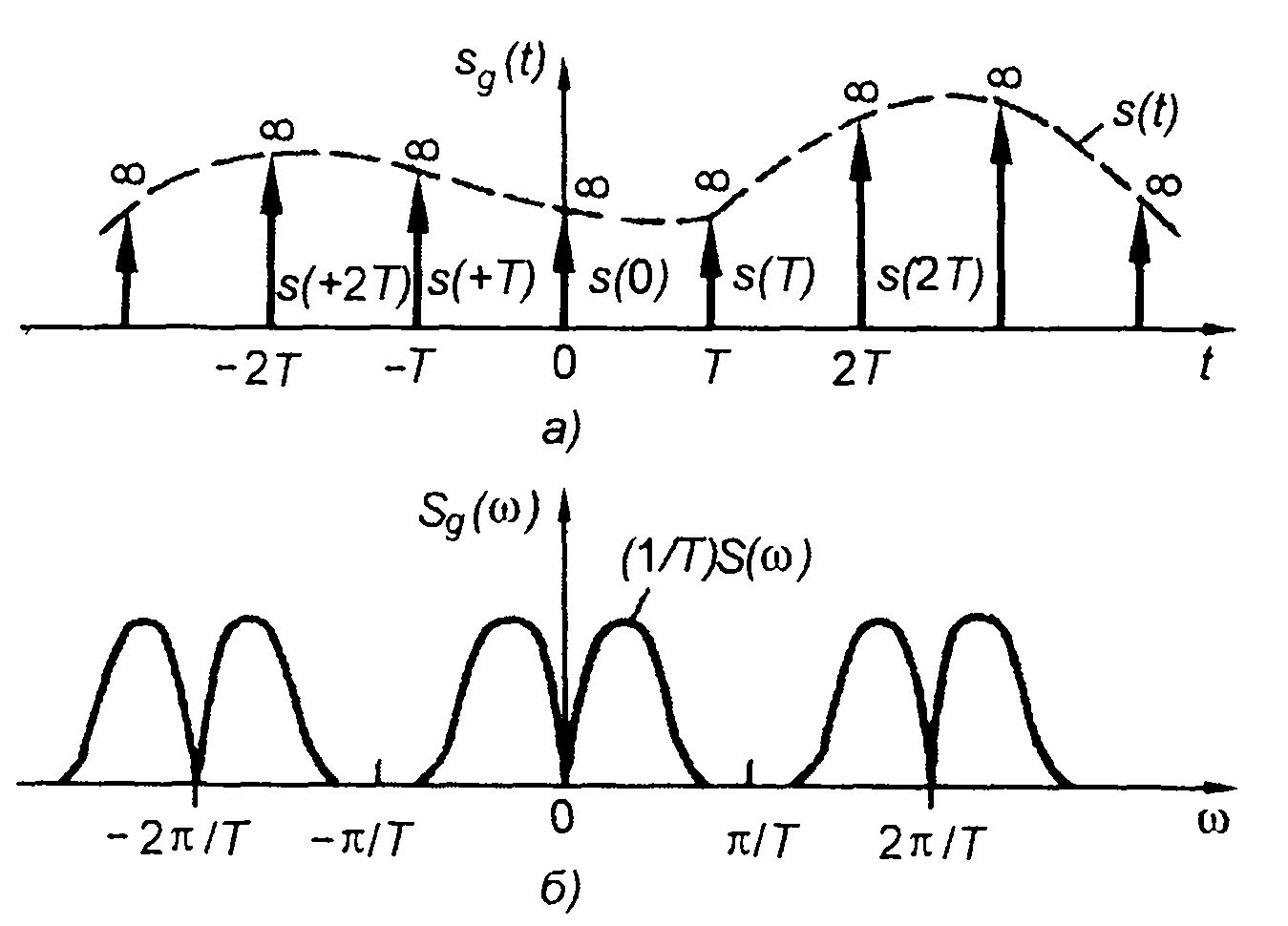
Рис. 6.3

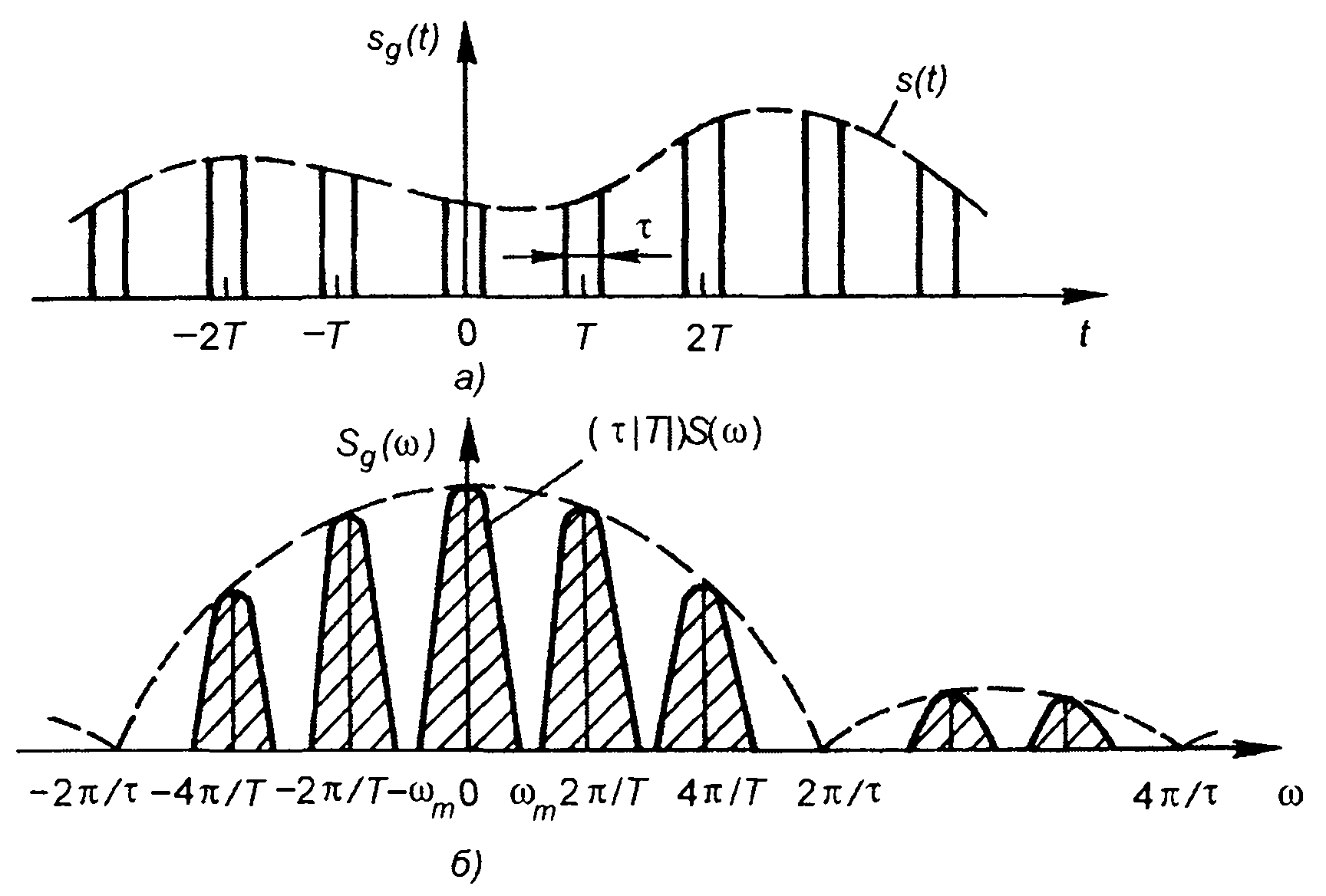
Рис. 6.4

Представляя сорбирующую последовательность прямоуголь­ных импульсов в виде ряда Фурье

(6.7)

где

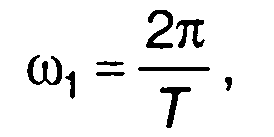
дискретный сигнал (6.6) запишем в виде

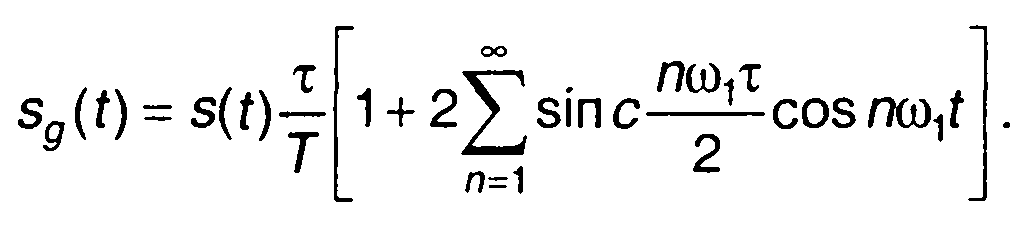(6.8)

Спектральная плотность сигнала s(t) найдется как преобразова­ние Фурье (6.8) (см. разд. 3)

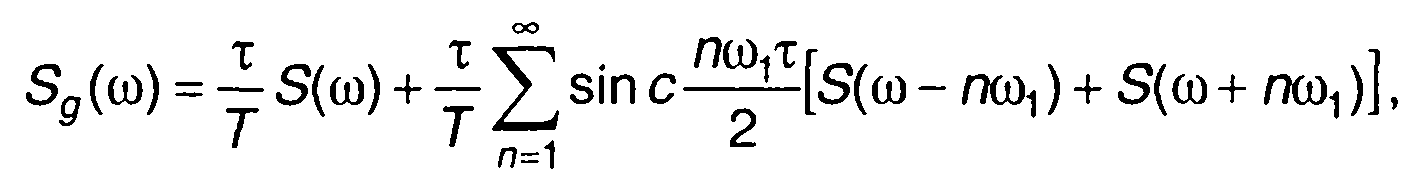(6.9)

где S(ω) - спектральная плотность сигнала s(t).

Как следует из (6.9), спектр дискретного сигнала получается по­вторением спектра исходного непрерывного сигнала через интер­вал, кратный ω₁=2π/T. Огибающая спектра дискретного сигнала определяется спектром стробирующих импульсов (рис. 6.4,б).

Одной из важных задач, решаемых при дискретизации сигналов, является выбор интервала дискретизации. Увеличение интервала может привести к безвозвратной потере информации о сигнале. С другой стороны, при уменьшении интервала дискретизации теряют­ся преимущества дискретизации. Представление о максимально допустимом интервале дискретизации можно получить из анализа спектра дискретного сигнала (рис. 6.3 и рис. 6.4). Непрерывный сиг­нал можно восстановить, пропуская дискретный сигнал через фильтр нижних частот. Верхняя частота полосы пропускания фильтра должна превышать максимальную частоту в низкочастот­ной части спектра сигнала. В то же время соседние составляющие спектра сигнала не должны перекрываться. Таким образом, интер­вал дискретизации должен выбираться из условия:

(6.10)

где ω_m = 2πf_m - максимальная частота в спектре сигнала.

Интервал дискретизации сигнала, определяемый (6.10), называ­ется интервалом Найквиста или Котельникова.

Возможна дискретизация и спектра сигнала. По аналогии с (6.10) условие дискретизации на оси частот может быть записано в виде

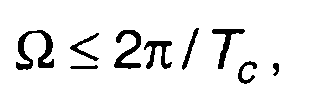(6.11)

где T_с - длительность сигнала.

При выполнении условия (6.11) восстановление спектра сигнала по его дискретным значениям производится без потерь.

6.3. Дискретное преобразование Фурье и его свойства

Спектральная плотность непрерывного сигнала определяется его преобразованием Фурье. Обратное преобразование позволяет найти временную функцию сигнала по его спектральной плотности. Дискре­тизация позволяет получить дискретный сигнал и соответствующий дискретный спектр. Однако для дискретного сигнала переход от вре­менного описания к спектру и обратно более удобно производить, используя дискретное преобразование Фурье (прямое и обратное).

Выражение для спектральной плотности дискретного сигнала, заданного на интервале [0,T_С], при достаточно малом значении интервала

дискретизации Т можем записать в виде

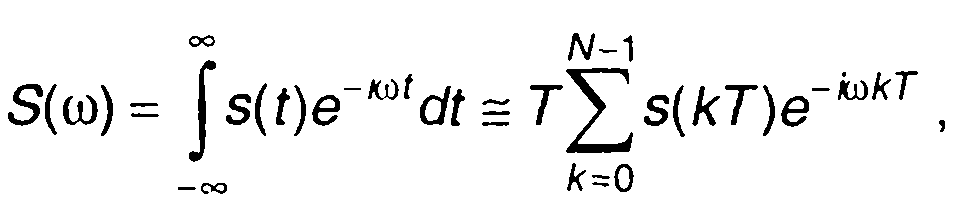(6.12)

где N - число интервалов дискретизации, N = Т_с/Т; Т_с - длитель­ность сигнала; Т- интервал дискретизации.

Если спектральная плотность сигнала S(ω) определяется для выборочных значений частоты ω = пΩ., то (6.12) примет вид

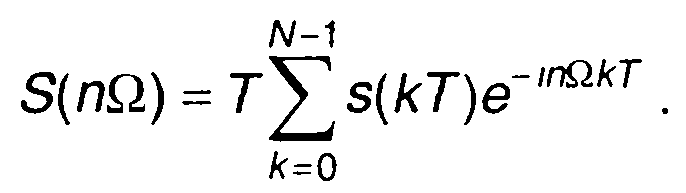(6.13)

Выражение (6.13) представляет дискретное преобразование Фу­рье (ДПФ). Аналогично для обратного ДПФ можно получить

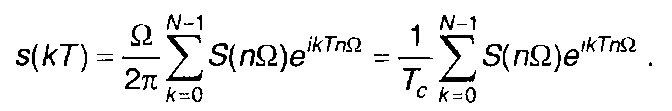(6.14)

В (6.12) и (6.13) N = Т_С/Т. С учетом (6.11) получим

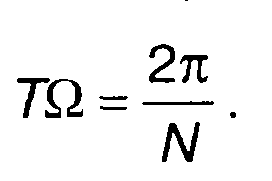(6.15)

Формулы ДПФ с учетом (6.15) обычно записываются в виде:

(6.16)

S_n является периодической функцией частоты с периодом, равным NΩ:

Дискретное преобразование Фурье связывает дискретный сиг­нал с его дискретным спектром, является удобным алгоритмом для численного расчета спектра сигнала по его временной функции

и сигнала (временной функции) по его спектру. При использовании ДПФ полезно учитывать его свойства. Они аналогичны свойствам преобразования Фурье - табл. 6.2.

Таблица 6.2

Свойства дискретного преобразования Фурье

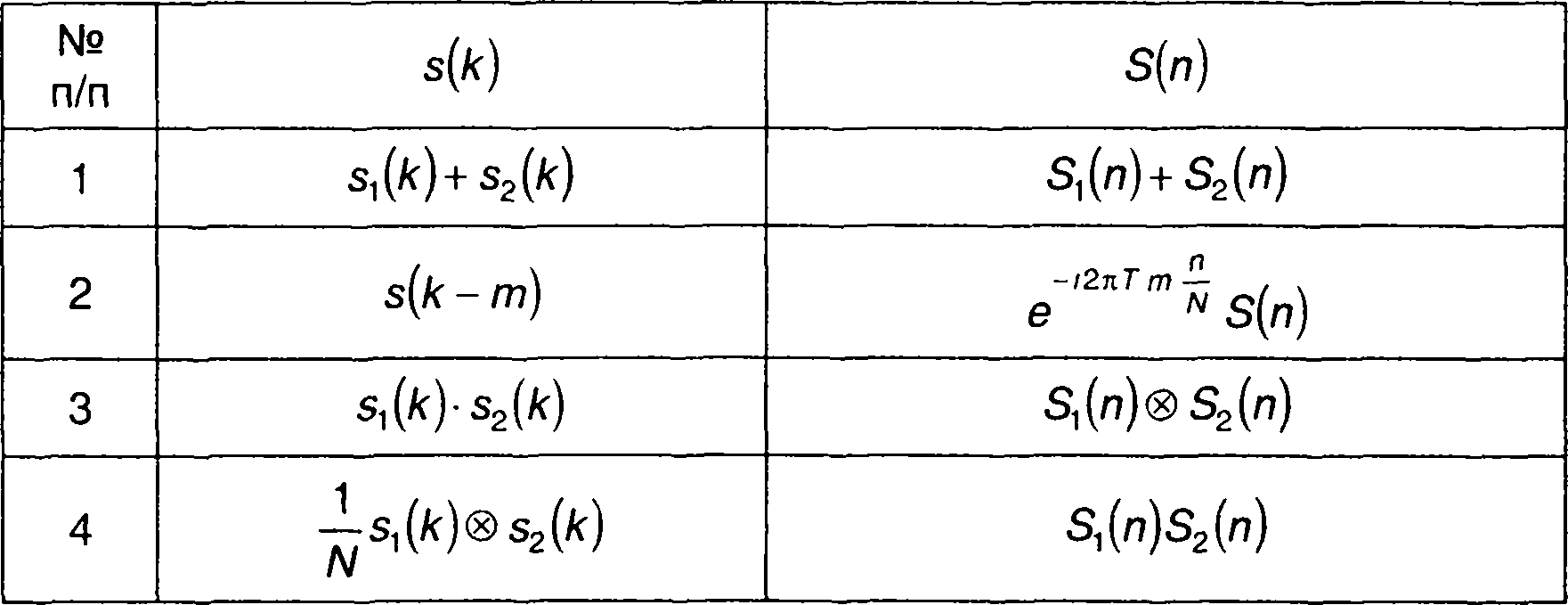
В качестве примера рассмотрим ДПФ сигнала в виде симмет­ричного треугольного импульса (рис. 6.5). Сигнал может быть пред­ставлен пятью выборочными значениями

Подставляя выборочные значения в (6.13), запишем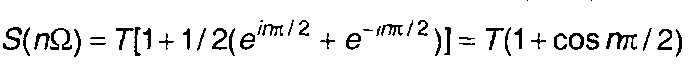

Таким образом,

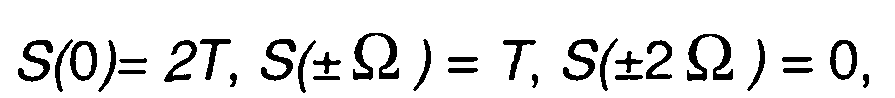
где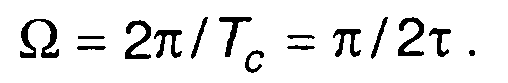

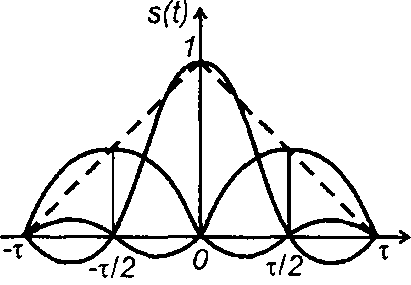
Рис. 6.5

Спектральная плотность исходного импульса описывается вы­ражением (разд. 3)

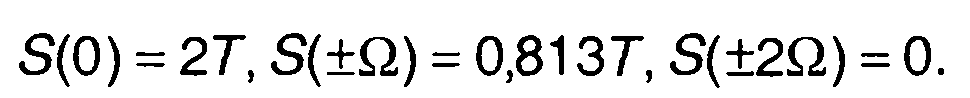
Из него получим

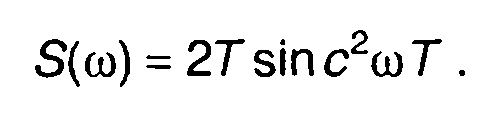
Отличие значений спектра, полученных с использованием пре­образования Фурье и ДПФ, определяет ошибку, появляющуюся при использовании ДПФ в качестве алгоритма расчета спектра сигнала.

6.4. Алгоритмы быстрого преобразования Фурье

Дискретное преобразование Фурье представляет алгоритм расче­та спектральных характеристик сигнала. Однако его использование часто связано с большим объемом вычислительных операций, что может приводить к значительной затрате времени. Сократить объем вычислительных операций при расчете ДПФ позволяет переход к алгоритмам быстрого преобразования Фурье (БПФ). Предложено несколько алгоритмов БПФ. В дальнейшем в качестве примера рас­смотрим алгоритм БПФ, обычно используемый при числе отсчетов N = 2ⁿ, где n - целое число.

Исходную последовательность выборочных значений сигнала разобьем на две части - с четными S_nч и нечетными номерами S_nн

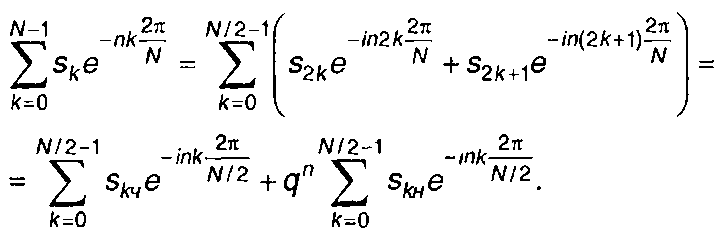(6.17)

Сомножитель qⁿ = е ^-in2π/N перед суммой второго слагаемого учитывает задержку s_kH относительно s_kч на один временной ин­тервал.

Выражение (6.17) представим в виде

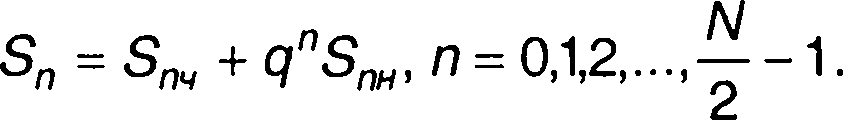(6.18)

Выражение (6.18) записано только для 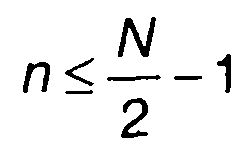. Чтобы определить S_n для больших значений n, используем свойство периодично­сти ДПФ

(6.19)

Для можем записать

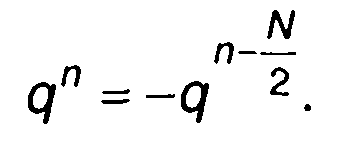(6.20)

С учетом (6.20) выражение для S_n при 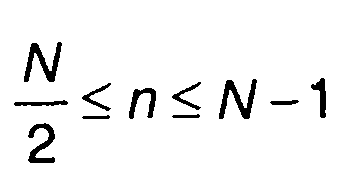получим

в виде

(6.21)

Таким образом, записаны выражения для расчета S_n: при n<N/2-1 выражение (6.18), при N / 2≤ n ≤ N — 1 выражение (6.21). В соответствии с записанными выражениями процесс вычисления ДПФ можно представить схематически как показано на рис. 6.6. Ум­ножение на q^m обозначено стрелкой с множителем, сложение - кру­жочками.

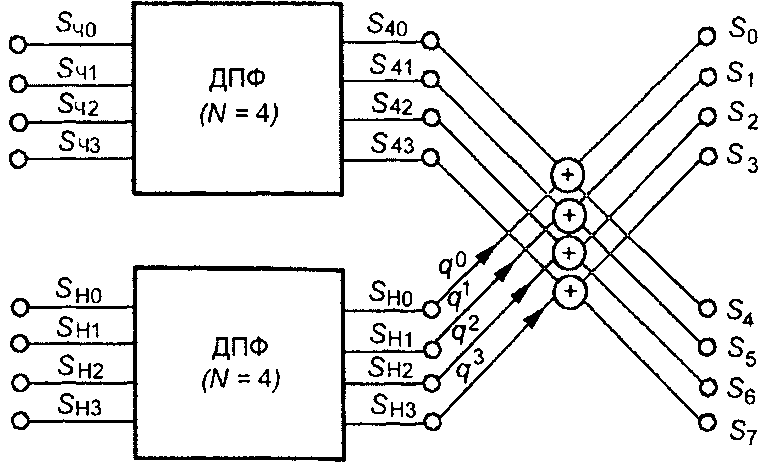
Рис. 6.6

Линии вверх от точки соответствуют сумме, вниз - разности вели­чин на входе. Дальнейшее уменьшение объема вычислений можно достичь разбиением каждой из последовательностей S_m и S_nH и т.д. до получения простейших двухэлементных последовательностей.

Найдя ДПФ двухэлементных последовательностей, можно опре­делить ДПФ четырехэлементных, восьмиэлементных и т.д. после­довательностей. Очевидно, что N должно быть равным 2" (л - це­лое число). Программы расчета ДПФ с использованием алгоритмов БПФ приведены во многих работах.

6.5. Дискретное преобразование Хартли и его свойства

По аналогии с ДПФ может быть введено в рассмотрение и дис­кретное преобразование Хартли (ДПХ). Прямое и обратное дис­кретные преобразования Хартли записываются в виде

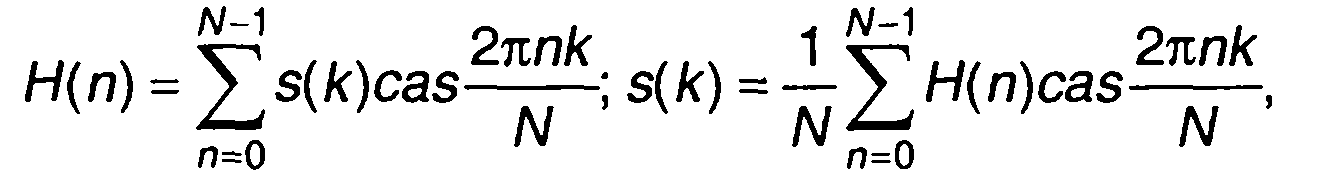(6.22)

где casx = cosx + sinx.

ДПФ S(n) и ДПХ Н(n) связаны между собой достаточно очевид­ными соотношениями

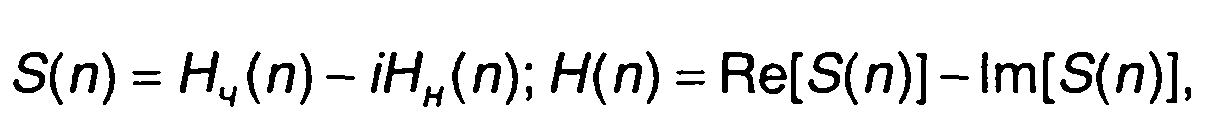(6.23)

где Н_ч(n) и Н_н(n) - четная и нечетная составляющие преобразова­ния Хартли:

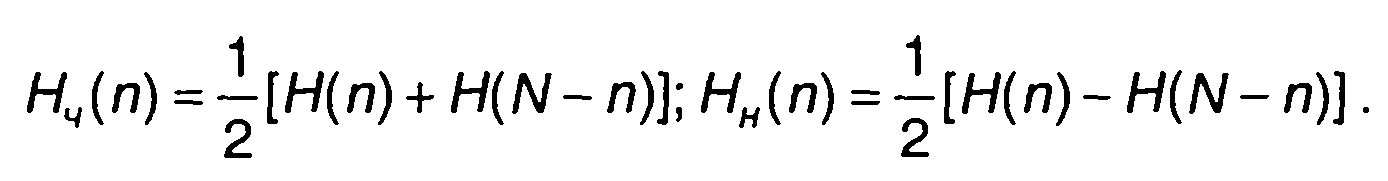(6.24)

При использовании ДПХ целесообразно учитывать его свойства. Основные свойства ДПХ приведены в табл. 6.3.

С целью сокращения времени расчетов при использовании пре­образования Хартли предложены алгоритмы быстрого преобразо­вания Хартли.

Преобразование Хартли для действительных функций s(t) дает действительные функции, что позволяет говорить об определенных удобствах ДПХ при использовании преобразования на инженерном уровне. К удобствам применения ДПХ следует отнести и симмет­ричность прямого и обратного преобразований. Усложнение выра­жений для ДПХ свертки и произведения функций по сравнению с ДПФ является отрицательным моментом.

6.6. Z-преобразование и его использование при анализе дискретных сигналов

6.6.1. Z-преобразование

Преобразование Лапласа, используемое при анализе непрерыв­ных сигналов, полезно и при анализе дискретных сигналов.

Для непрерывного сигнала преобразование Лапласа имеет вид

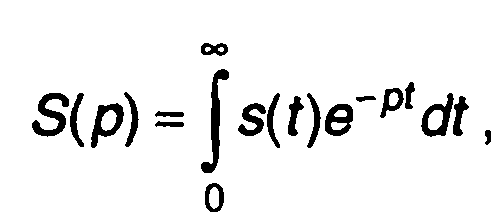(6.25)

где р - комплексная величина.

Таблица 6.3

Свойства дискретного преобразования Хартли

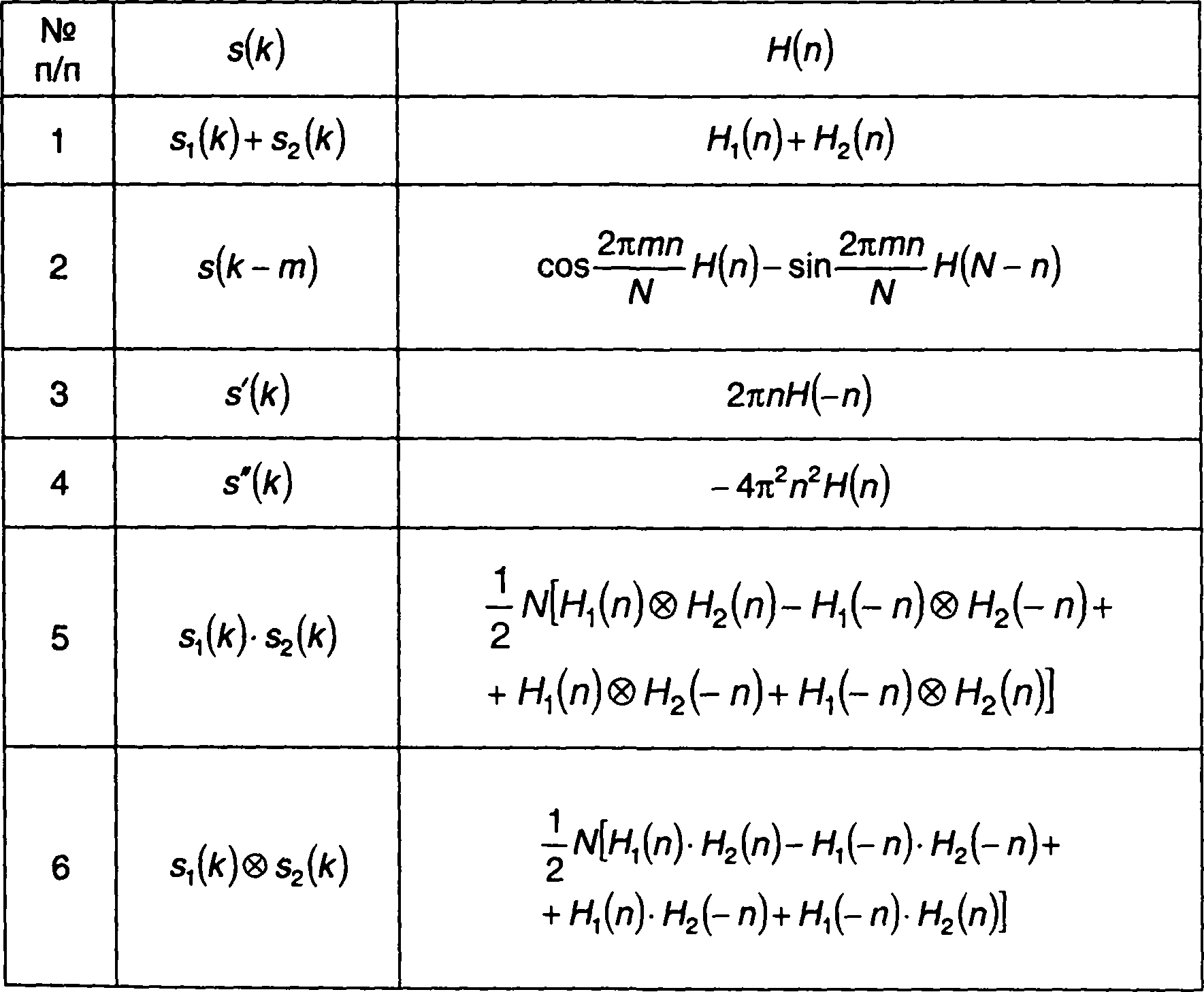
Для дискретного сигнала

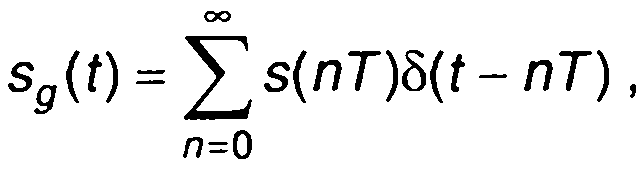(6.26)

из (6.25) получим

(6.27)

Выражение (6.27) является дискретным преобразованием Лап­ласа. Обозначив е^pТ = z, выражение (6.27) запишем в виде

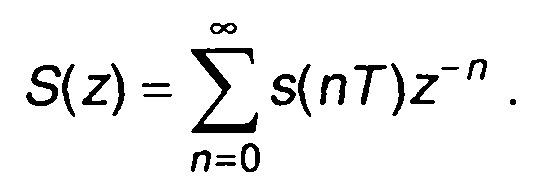(6.28)

Записанное выражение представляет z-преобразование дис­кретного сигнала s(nT). Исходя из условия существования преобра­зования Лапласа (разд. 4) можно записать условие существования и z-преобразования. Z-преобразование существует, если величина |s(nT)| возрастает медленнее степенной функции

(6.29)

Область сходимости ряда (6.28) включает всю плоскость, за ис­ключением круга радиуса r. Величина r называется радиусом схо­димости.

Примеры z-преобразований некоторых видов сигналов.

1. Сигнал, описываемый экспоненциальной функцией.

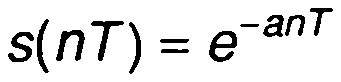
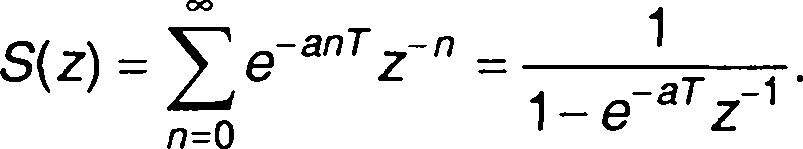
2. Гармонический сигнал.

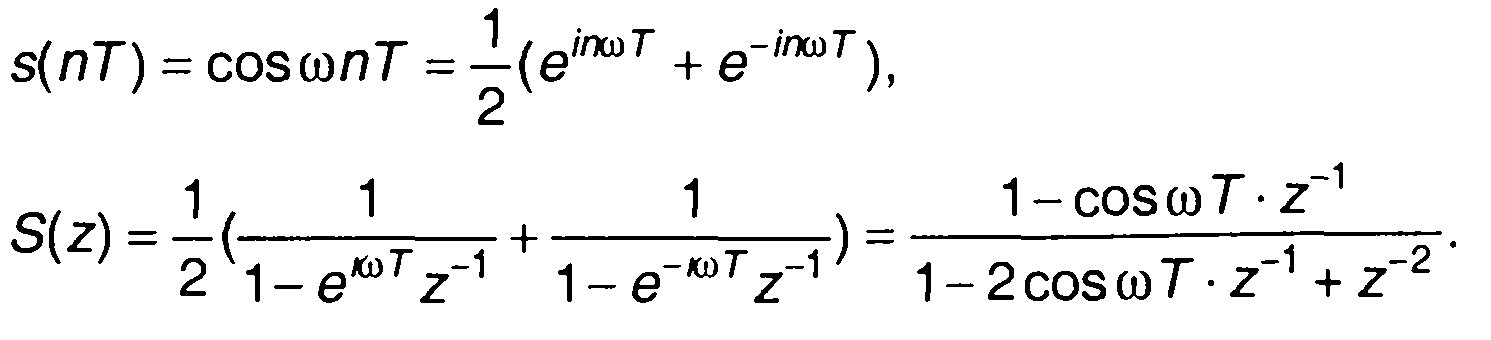
3. Сигнал, описываемый степенной функцией.

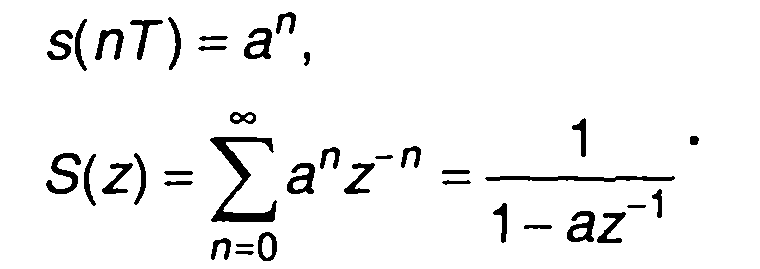
Расширяет число примеров табл. 6.4.

Имея z-преобразование дискретного сигнала, можно получить спектр сигнала. Для этого необходимо сделать подстановку

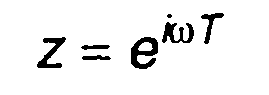(6.30)

в z-преобразование сигнала.

Определение сигнала s(nT) по S(z) производится с помощью об­ратного z-преобразования. Обратное z-преобразование получается подстановкой е^pT = z в обратное преобразование Лапласа

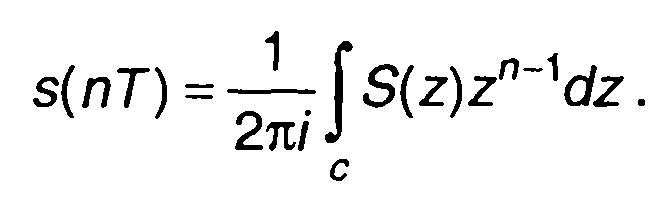(6.31)

При решении (6.31) используются различные методы, чаще все­го метод вычетов и метод разложения на простые дроби (разд. 4).

Метод вычетов. Если S(z) является действительной функцией переменного z, то (6.31) можно решить с помощью теоремы о выче­тах (разд. 4)

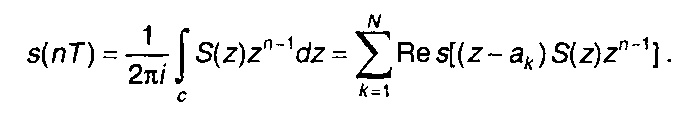(6.32)

Таблица 6.4

Z-преобразоеания сигналов

Пример. z-Преобразование имеет вид:

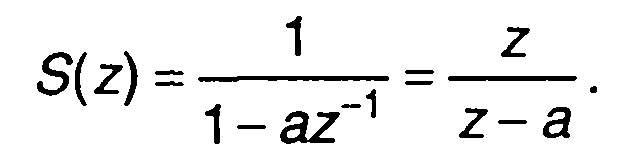
Подставляя выражение для S(z) в (6.32), получаем

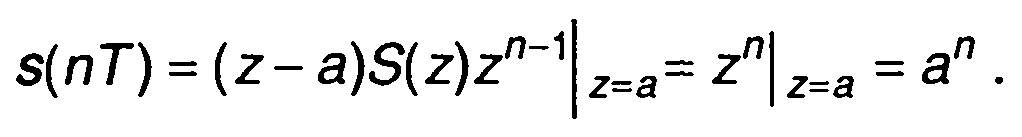
Метод разложения на простые дроби.

Если S(z) представляет рациональную функцию z или z-1, ее разложение на простые дроби имеет вид

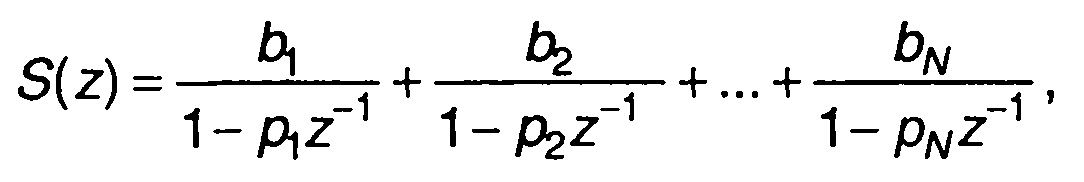(6.33)

где полюсы р_к. различны, т.е. р_к ≠ р_т при к ≠ т,

Сигнал s(nT) получается суммированием обратных z-

преобразований каждого члена (6.33). Таким образом,

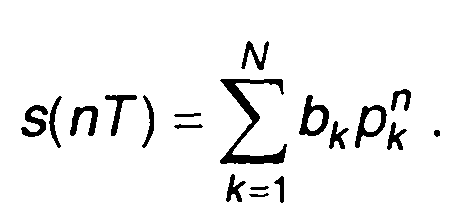(6.34)

Z-преобразование, являясь одной из форм преобразования Ла­пласа, обладает аналогичными свойствами. Использование свойств z-преобразования позволяет упростить анализ дискретных сигналов.

6.6.2. Свойства z-преобразования

Из свойств z-преобразования прежде всего отметим следующие.

1. Аддитивность.

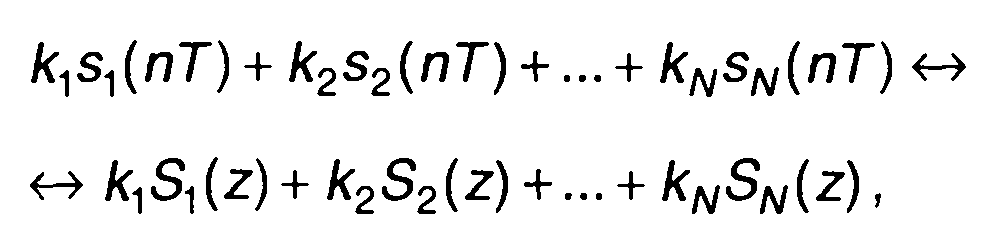(6.35)

где k_п - постоянные коэффициенты; <-> - знак соответствия вре­менной и z-функций.

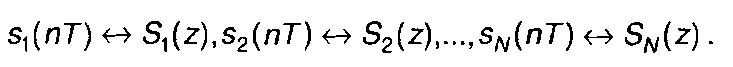(6.36)

2. Задержка во времени.

Для

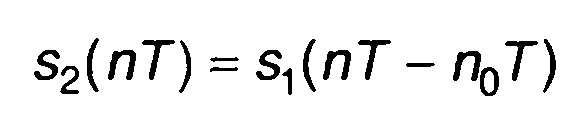(6.37)

имеем

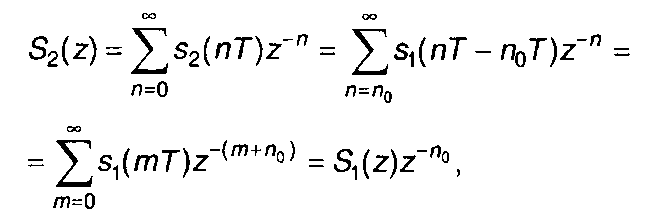(6.38)

где n - n₀ = т.

Таким образом,

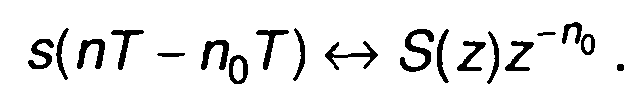(6.39)

При n₀ = 1

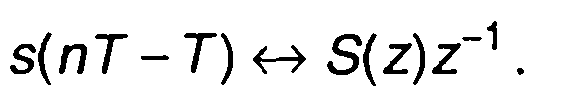(6.40)

Как следует из (6.40), задержке сигнала на интервал дискрети­зации Т соответствует умножение z-преобразования сигнала на z^-1. С учетом (6.40) можем получить z-преобразование разности

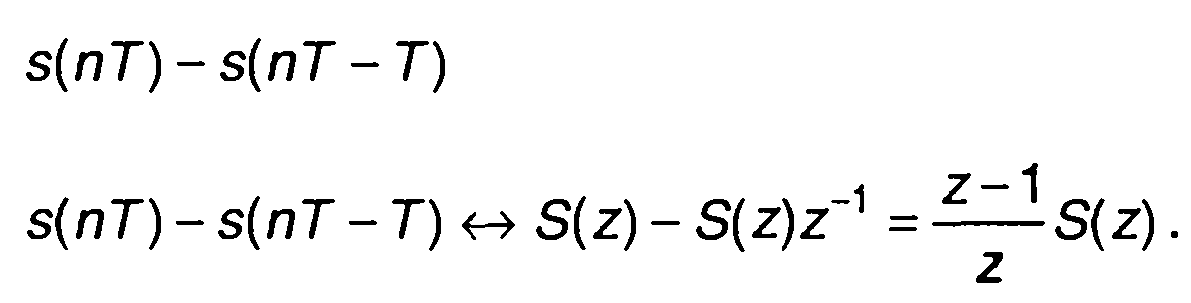(6.41)

3. Свертка дискретных сигналов.

Свертка дискретных сигналов описывается выражением

(6.42)

или

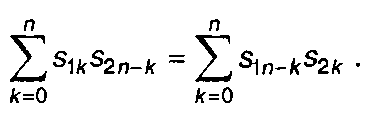(6.43)

Выражение для z-преобразования свертки

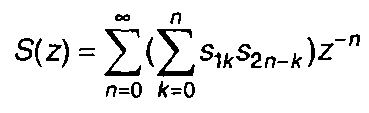(6.44)

запишем в виде

(6.45)

При k > n, s_2n-k = 0, верхний предел второй суммы можно заме­нить на. После обозначения n - к - т, выражение для S(z) при­мет вид

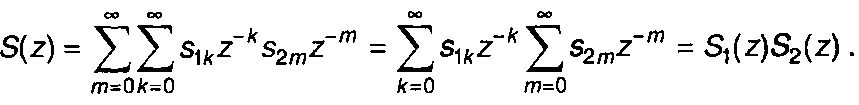(6.46)

Таким образом, получим

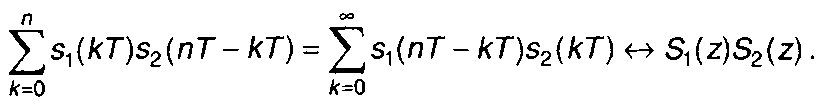(6.47)

Рассмотренные свойства z-преобразования и некоторые другие приведены в табл. 6.5.

Таблица 6.5

Свойства z-преобразования

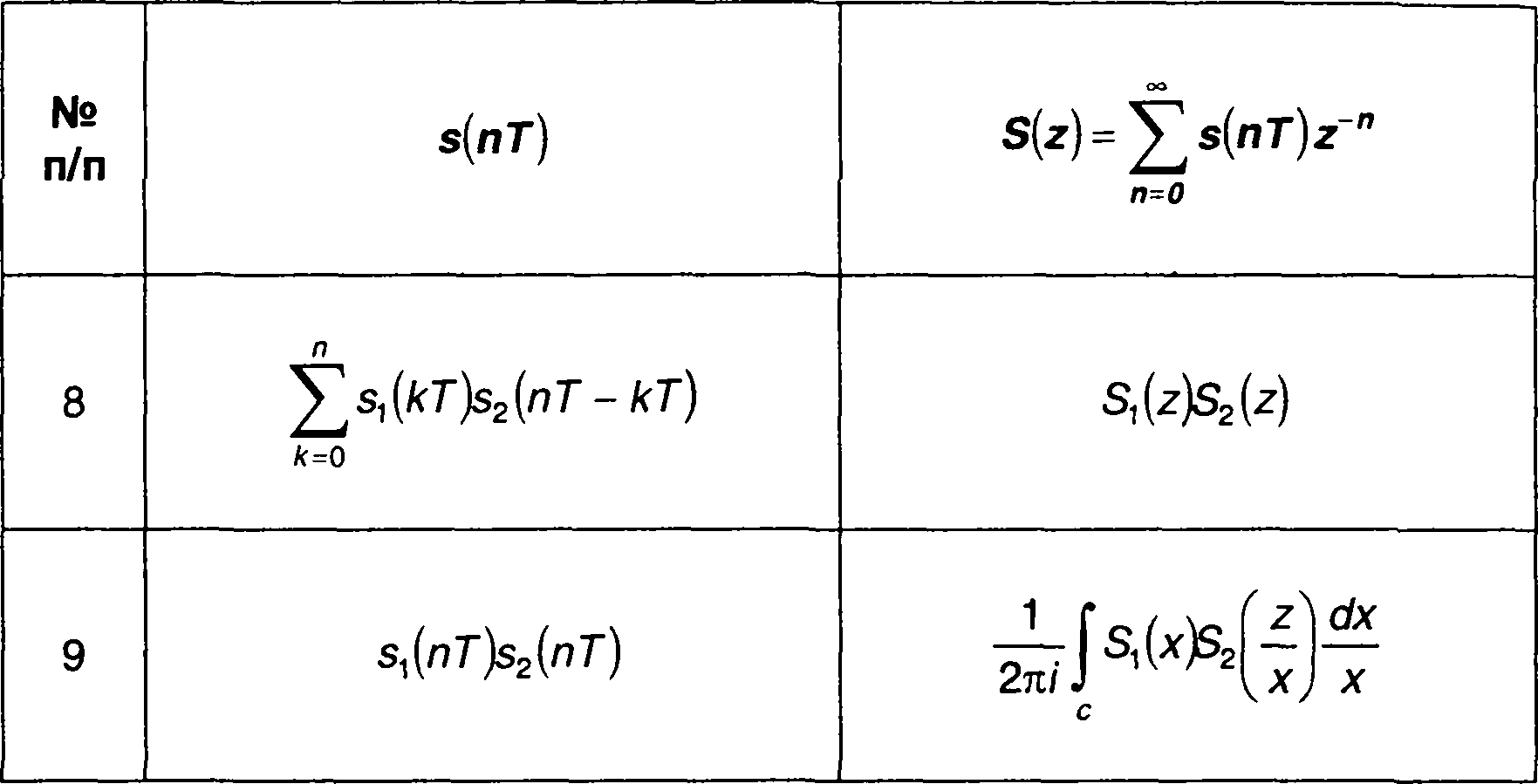
6.7. Восстановление непрерывного сигнала по дискретным значениям

Задача восстановления сигнала по его дискретным значениям в математическом плане сводится к отысканию функции, описы­вающей сигнал, которая в заданные моменты времени принимает заданные значения (равные дискретным значениям сигнала), а в остальные моменты описывает сигнал с какой-то степенью точно­сти. Указанная операция без конкретизации физического содержа­ния рассматриваемой функции составляет содержание общей за­дачи интерполяции. К интерполяции временной функции сигнала приходится прибегать и тогда, когда известно аналитическое опи­сание сигнала, но функция, описывающая сигнал, является слож­ной, имеются определенные трудности ее расчета. В этом случае вычисляют значения сигнала для нескольких моментов времени и по ним строят более простую (интерполирующую) функцию, с по­мощью которой определяют значения сигнала в остальных точках. Так же можно поступать и при задании сигнала с помощью графика (осциллограммы).

6.7.1 Интерполяционные многочлены

Определение непрерывного сигнала по его дискретным значе­ниям означает восстановление сигнала. В математическом отно­шении эта операция сводится к описанию временной функции сигнала s(t), заданной своими значениями в заданные моменты времени, с помощью функции φ(f), принимающей те же значения

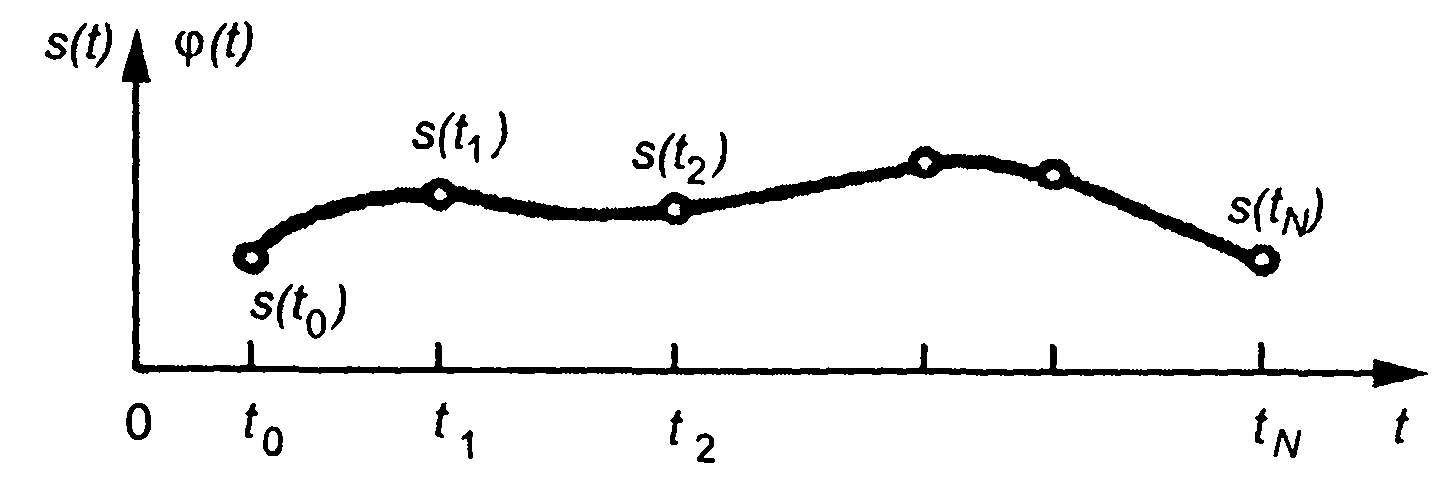
Рис. 6.7

в указанные моменты времени (рис. 6.7). Функцию φ(7) называют интерполирующей, точки, в которых заданы значения функции, уз­лами интерполяции.

Чаще всего интерполирующую функцию задают в виде много­члена

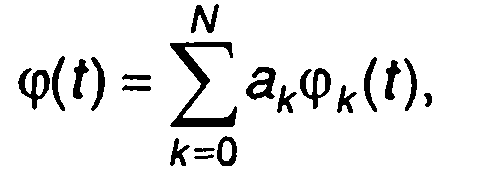(6.48)

где φ_k(t) - базисные функции; а_к-постоянные коэффициенты.

При заданной совокупности базисных функций φ_k(t) интерполи­рующая функция ф(7) определяется только коэффициентами а_к.

Найти коэффициенты можно, составив систему уравнений, исполь­зуя (6.48), записанных для заданных моментов времени (для кото­рых известны значения сигнала)

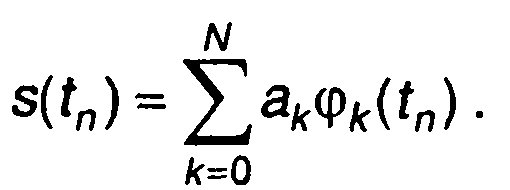(6.49)

Матрица системы уравнений имеет вид

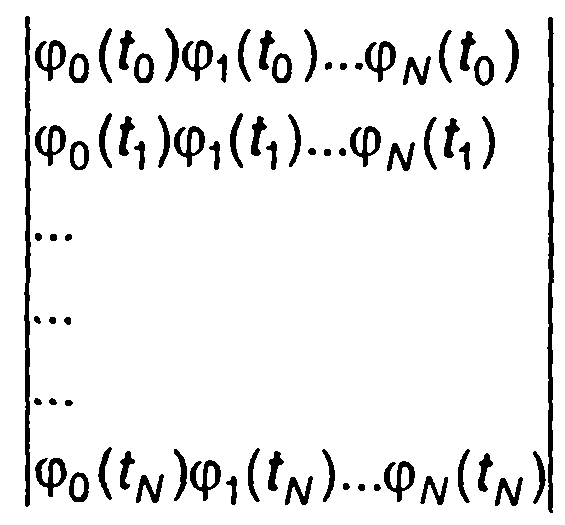(6.50)

При написании матрицы учтено, что для однозначного опреде­ления коэффициентов необходимо, чтобы число строчек матрицы было равно числу столбцов.

Выражение для а_к получится в виде

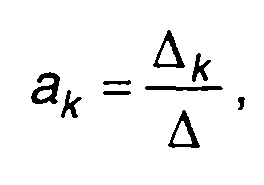(6.51)

где ∆ - определитель матрицы; ∆_к получается из ∆ путем замены k-го столбца столбцом s(t_k).

Таким образом, интерполирующая функция будет определяться выражением

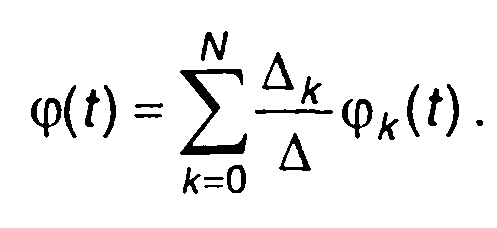(6.52)

Раскладывая определитель ∆_k, по элементам k-го столбца, вы­ражение для а_k получим в виде

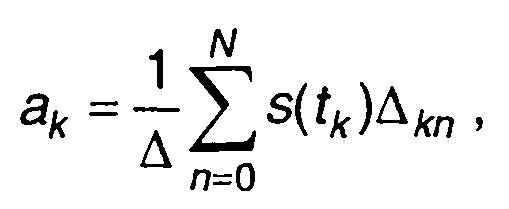(6.53

где ∆_kn - соответствующее алгебраическое дополнение.

С учетом (6.53) из (6.52) получим другую форму записи интерполяционного многочлена

(6.54)

Коэффициенты ряда (6.54) представляют значения s(t) в узлах интерполяции. Функции Ф_k(t) определяются базисными функциями φ_k(t) и узлами интерполяции (t₀,t₁,..t_N). Очевидно равенство

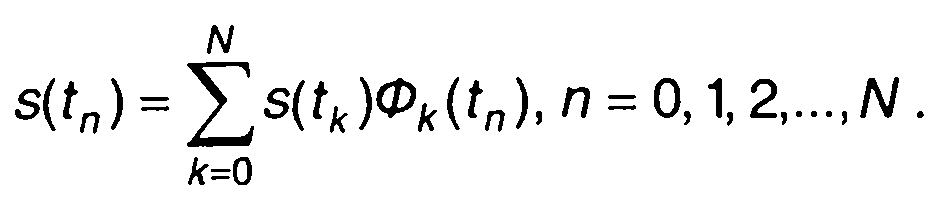(6.55)

Как следует из (6.55), функция Ф_k(t) должна удовлетворять условию

)

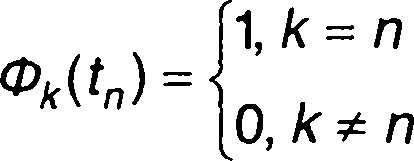(6.56)

Форма представления интерполирующей функции (6.54) являет­ся наиболее удобной для практического использования; в ней в ка­честве коэффициентов многочлена фигурируют выборочные значе­ния сигнала.

Качество интерполяции функции при заданных узлах интерполя­ции зависит только от выбора интерполяционных многочленов. Ин­терполяционными многочленами могут быть степенные многочлены, ортогональные многочлены и сплайновые функции. В радиотехнике чаще используется ряд Котельникова. Одно из основных его досто­инств связано с тем, что в качестве коэффициентов ряда использу­ются дискретные значения, которыми задается сигнал.

В настоящем разделе рассматриваются интерполирующие функции на основе степенных многочленов, многочленов Лагранжа и функций Котельникова. В разд. 7 рассматривается сплайновая интерполяция.

6.7.2. Степенные многочлены, многочлены Лагранжа

В выражении для интерполирующей функции (6.48) в качестве интерполяционного многочлена может быть использован степенной многочлен. Степенной многочлен, описывающий сигнал, запишем в виде

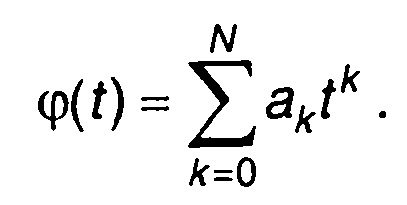(6.57)

Графики базисных функций многочлена даны на рис. 6.8. Они определены на всей оси времени, неограниченно возрастают с увеличением порядкового номера.

Матрица системы уравнений (6.50) в этом случае примет вид

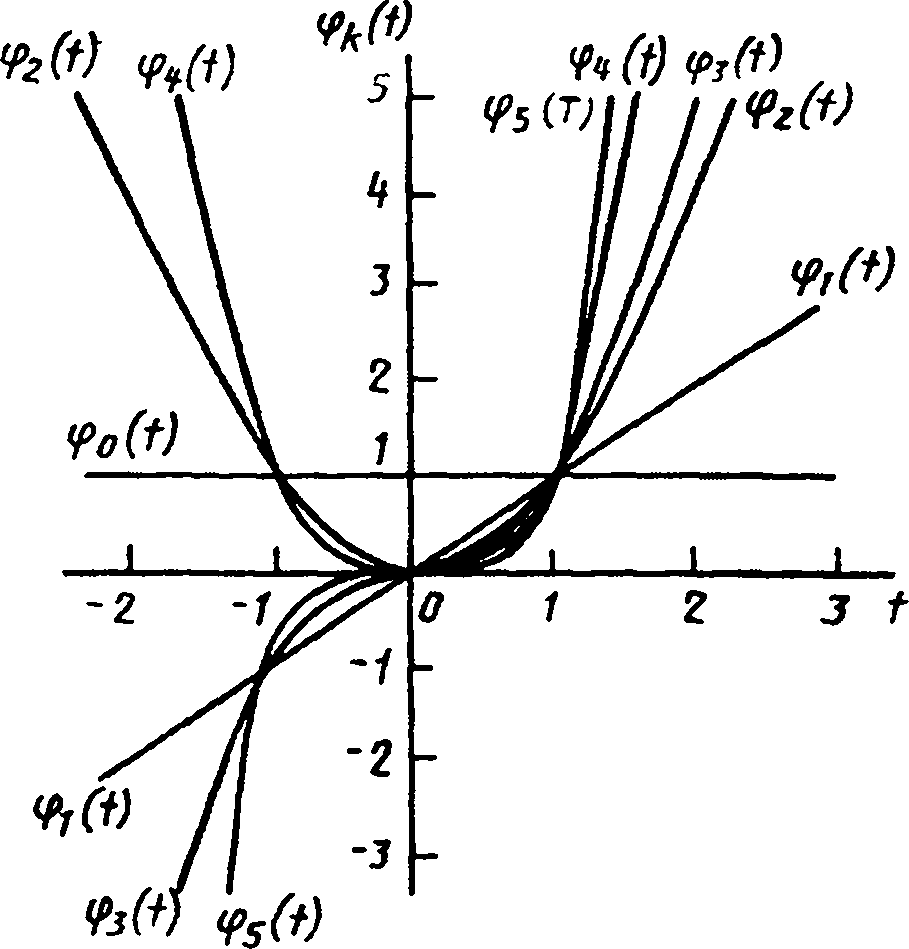
Рис. 6.8

Матрица дает определитель Вандермонда или степенной опре­делитель. Переходя к форме записи многочлена (6.54), выражение для базисных функций получим в виде

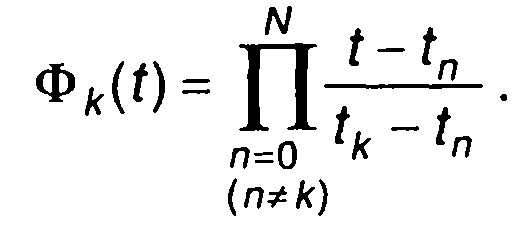(6.58)

Таким образом, интерполирующая функция φ(t) будет описы­ваться выражением

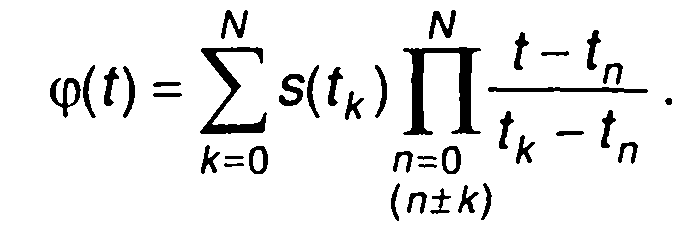(6.59)

Многочлен (6.59) называется интерполяционным многочленом Лагранжа. При постоянном шаге по оси t, когда t₁-t₀ = t₂ - t₁=... = t_N- t_N_₁ = h, обозначив t-t₀/h-x, запишем

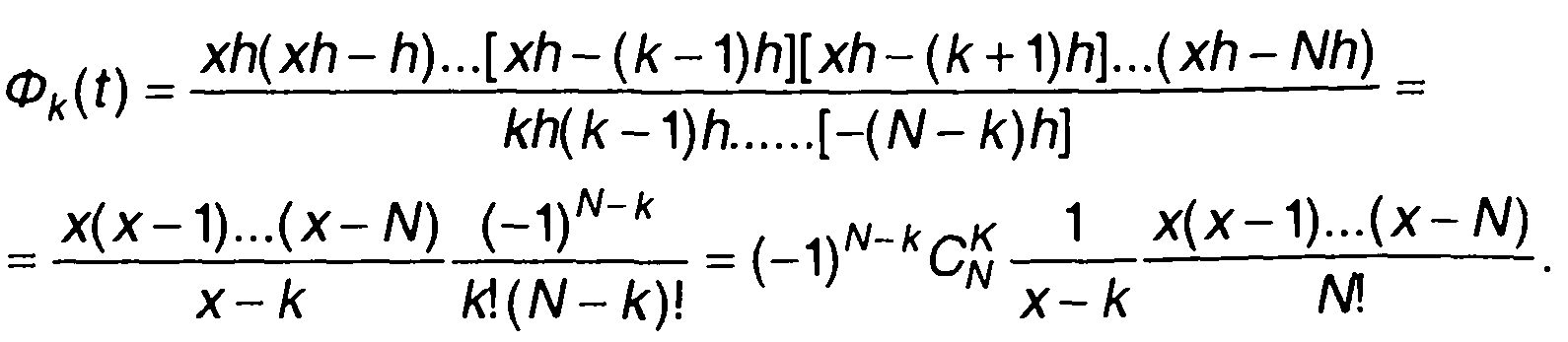(6.60)

Таким образом, выражение для интерполяционного многочлена Лагранжа примет вид:

(6.61)

Интерполяционный многочлен Лагранжа φ(t) совпадает с ис­ходной функцией, описывающей сигнал s(t) в узлах интерполяции t₀,t₁...t_n. В остальных точках он будет отличаться от s(t). Исключе­ние составляет тот случай, когда сигнал описывается степенным многочленом степени не выше N. В этом случае φ(t) и s(t) будут тождественно равны.

Многочлен Лагранжа обладает хорошими интерполяционными сойствами при сравнительно небольшом числе узлов интерполя­ции. При большой степени многочлена (на практике N > 5) возника­ют трудности вследствие "раскачки" полинома между узлами ин­терполяции.

Отличие ср(0 от s(t) определяет погрешность интерполяции. По­грешность оценивается неравенством

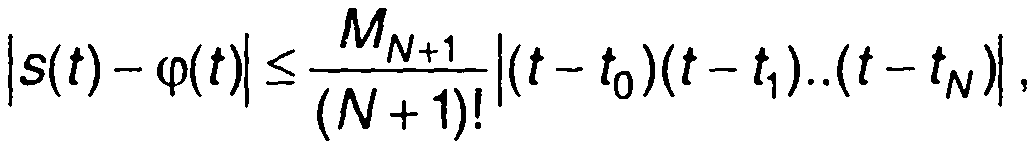(6.62)

где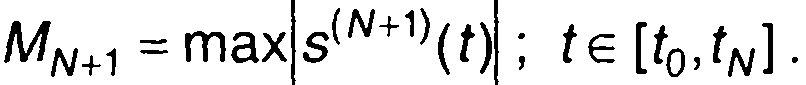

Как следует из (6.62), погрешность интерполяции сигнала опре­деляется значениями (N+1) -производной интерполируемой функ­ции и многочлена

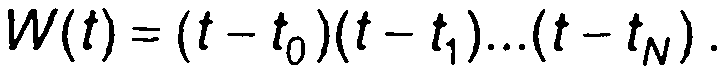(6.63)

Многочлен W(t) обращается в нуль в узлах интерполяции t₀,t₁...t_n. Переходя через нули, меняет знак, принимая в интерва­лах между ними экстремальные значения (рис. 6.9), значения экс­тремумов будут различны. В районе больших экстремумов можно ожидать больших погрешностей. Погрешность будет особенно ве­лика для значений вне интервала [t₀,t_N], т.е. в том случае, когда многочлен Лагранжа используется для экстраполяции функции.

Примеры интерполяции функций с использованием многочлена Лагранжа приведены в конце разд. 7.

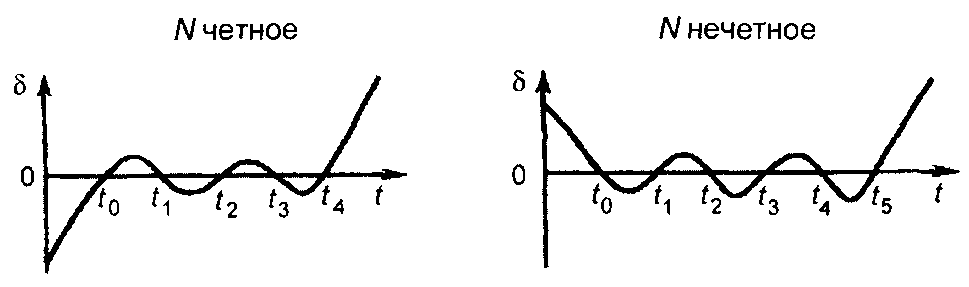
Рис. 6.9

6.7.3. Ряд Котельникова

Для восстановления непрерывного сигнала s(t) по его дискрет­ным значениям в радиотехнике чаще всего используется ряд Ко­тельникова

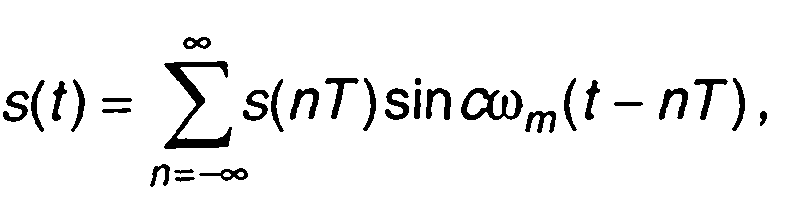(6.64)