ДЕТЕРМИНИРОВАННЫЕ СИГНАЛЫ 8 страница

Для описания узкополосного сигнала используется и комплекс­ная форма записи

(8.2)

где

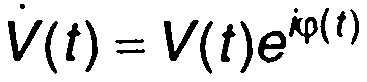(8.3)

- комплексная огибающая сигнала.

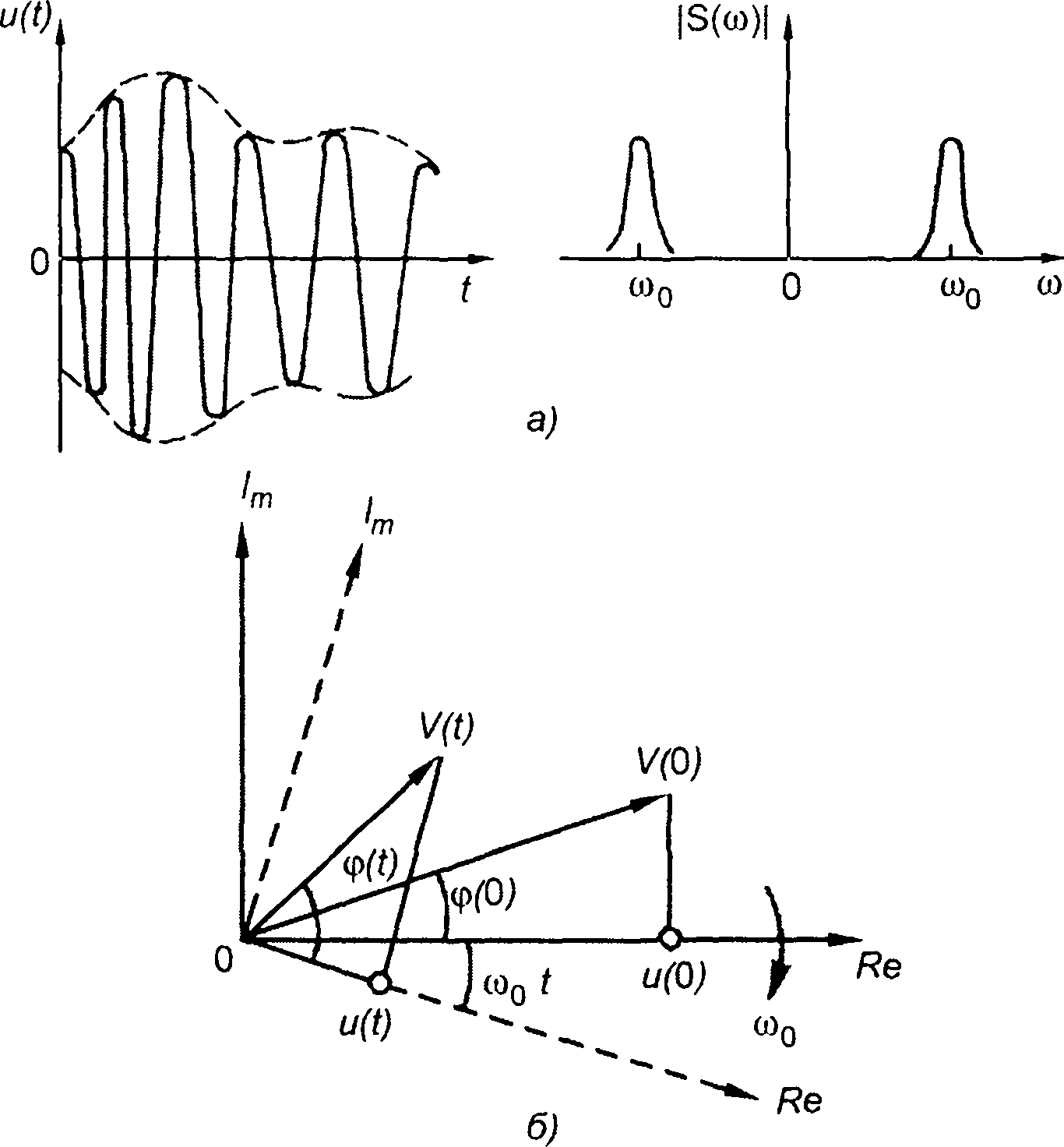
Рис. 8.1

Как следует из (8.2), узкополосный сигнал определяется несу­щей частотой ω₀ и комплексной огибающей V(t).

Комплексная огибающая сигнала может быть представлена в виде

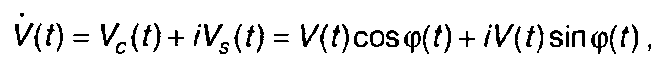(8.4)

где V_c(t) = V(t)cosφ(t), V_s(t) = V(t)sinφ(t) - квадратурные состав­ляющие сигнала.

С учетом (8.4) получим

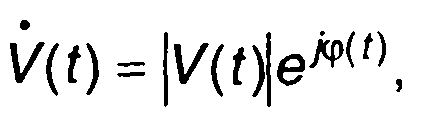
Где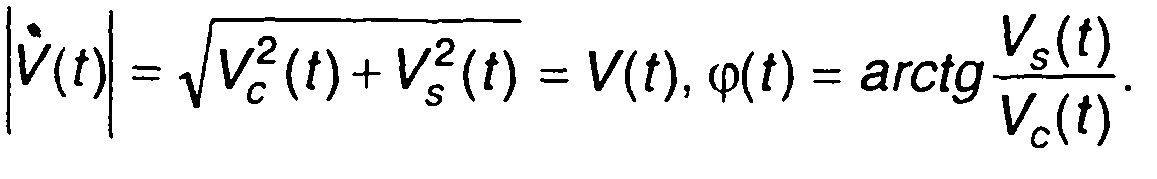

Графически комплексный сигнал V(t) изображается в виде век­тора на комплексной плоскости длины V(t) (рис. 8.1,6). Вектор со­ставляет угол φ(t) с действительной осью. Длина вектора V(t) и угол между вектором и действительной осью φ(t) изменяются во време­ни. Сама система координат вращается по часовой стрелке с угло­вой скоростью φ₀. Узкополосному сигналу соответствует проекция вектора на действительную ось.

8.2. Сумма и произведение узкополосных сигналов

При анализе узкополосных сигналов, в частности, при анализе прохождения их через цепи, в ряде случаев приходится рассматри­вать сумму узкополосных сигналов и их произведение. Запишем выражения, описывающие их.

Сумма двух узкополосных сигналов с одинаковой несущей час­тотой ω₀

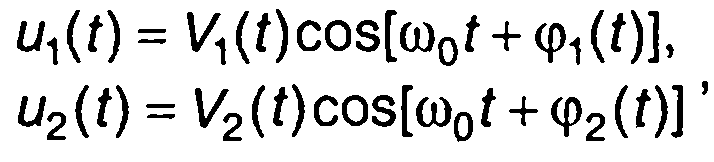(8.5)

представляет также узкополосный сигнал с той же частотой ω₀

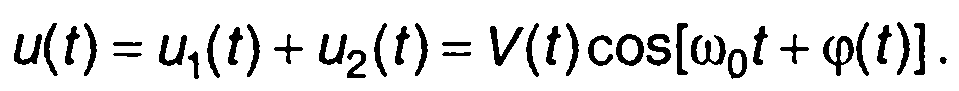(8.6)

Выражение для u(t) с использованием комплексной формы мож­но записать в виде

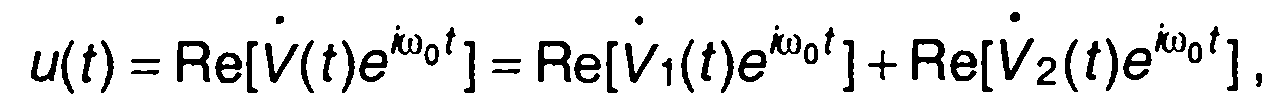(8.7)

гдeV^(t), V2(t) - комплексные огибающие сигналов u₁(t), u₂(t).

Комплексная огибающая суммарного сигнала равна сумме ком­плексных огибающих исходных сигналов

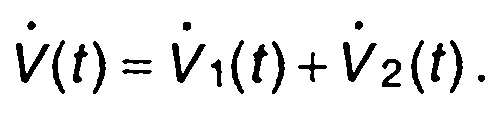(8.8)

Огибающая суммарного сигнала определяется выражением

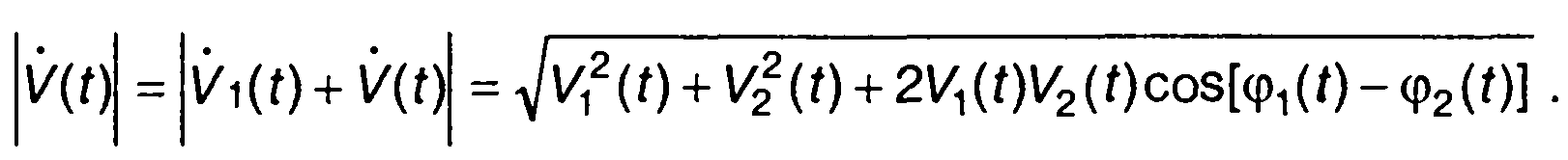(8.9)

Произведение двух узкополосных сигналов с несущими частота­ми ω₁ И ω₂

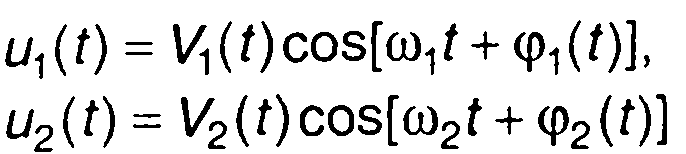
запишем в виде

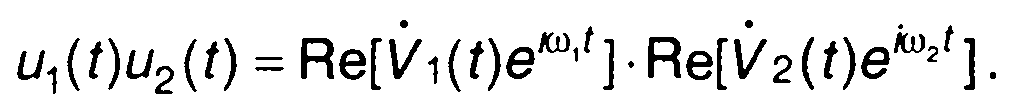(8.10)

Для произвольных комплексных величин z₁ и z₂ имеет место следующее равенство:

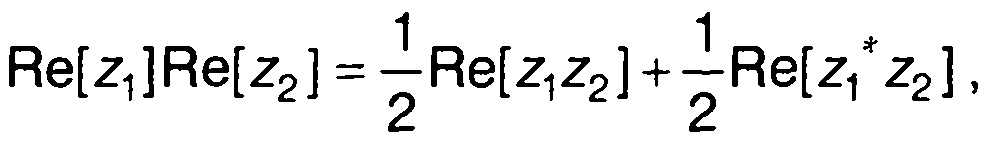(8.11)

где z - комплексно-сопряженная величина.

С учетом (8.11) для произведения узкополосных сигналов получим

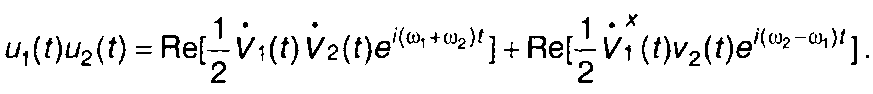(8.12)

Произведение узкополосных сигналов представляет сумму двух сигналов (8.12), один из которых имеет несущую частоту, равную сумме частот ω₁ и ω₂ , а второй имеет несущую частоту, равную разности частот ω₁ и ω₂ .

8.3. Спектр узкополосного сигнала

Спектральная плотность узкополосного сигнала u(t) определяет­ся его преобразованием Фурье

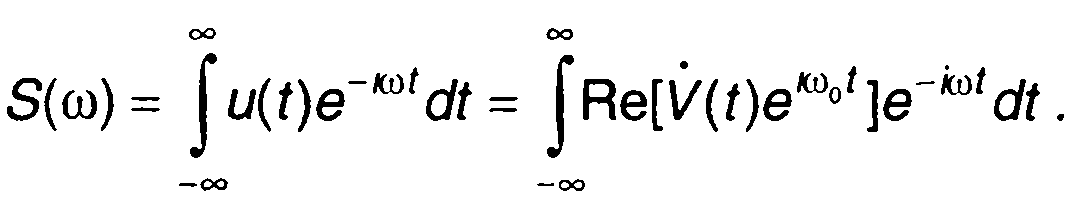(8.13)

Действительную часть комплексной величины z можно предста­вить в виде

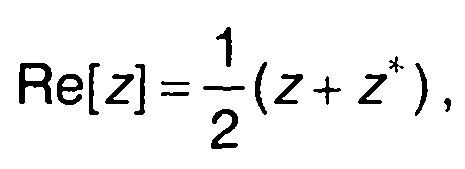(8.14)

где z* - комплексно-сопряженная величина.

С учетом (8.14) из (8.13) получим

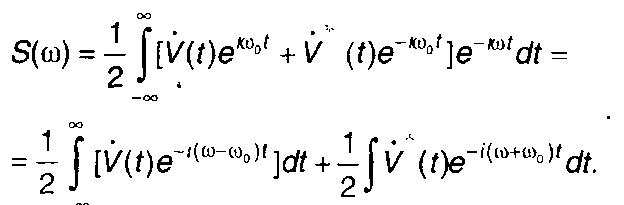(8.15)

Величина

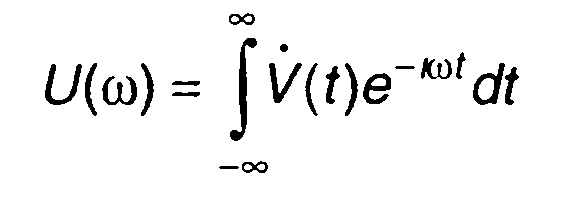(8.16)

представляет спектральную плотность комплексной огибающей сигнала. Таким образом, спектральная плотность узкополосного сигнала определяется спектральной плотностью комплексной оги­бающей, соотношением, которое следует из (8.15)

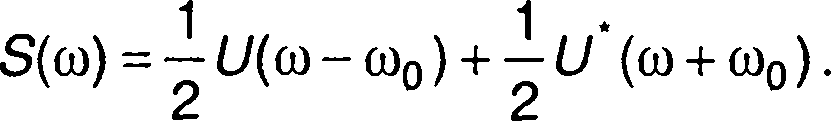(8.17)

Спектральную плотность комплексной огибающей можно пред­ставить в виде

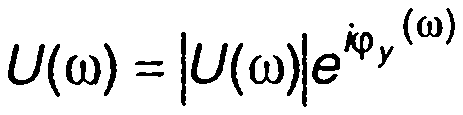(8.18)

где |U(ω)|, φ_у(φ) - амплитудный и фазовый спектры комплексной огибающей сигнала (рис. 8.2,а).

Спектр комплексной огибающей сосредоточен в области низких частот. Спектр узкополосного сигнала S(ω) получается путем пере­носа спектра комплексной огибающей U(ω) из окрестности нулевой частоты в окрестность несущей частоты ±ω₀ (с коэффициентом 1/2), рис. 8.2,6.

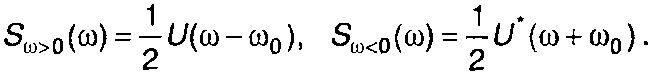(8.19)

Спектры в области положительных и отрицательных частот не должны заходить за начало координат, что и определяет условие узкополосности.

Примеры.

1 .Спектральной плотности комплексной огибающей сигнала (рис. 8.3,а)

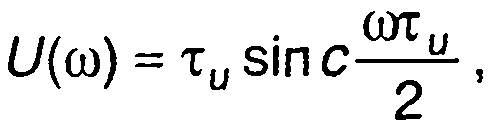
где τ_u - параметр зависимости (длительность сигнала), соответствует спектральная плотность сигнала (ω > 0), рис. 8.3,6,

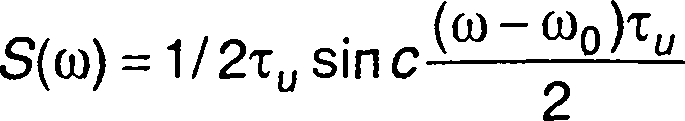
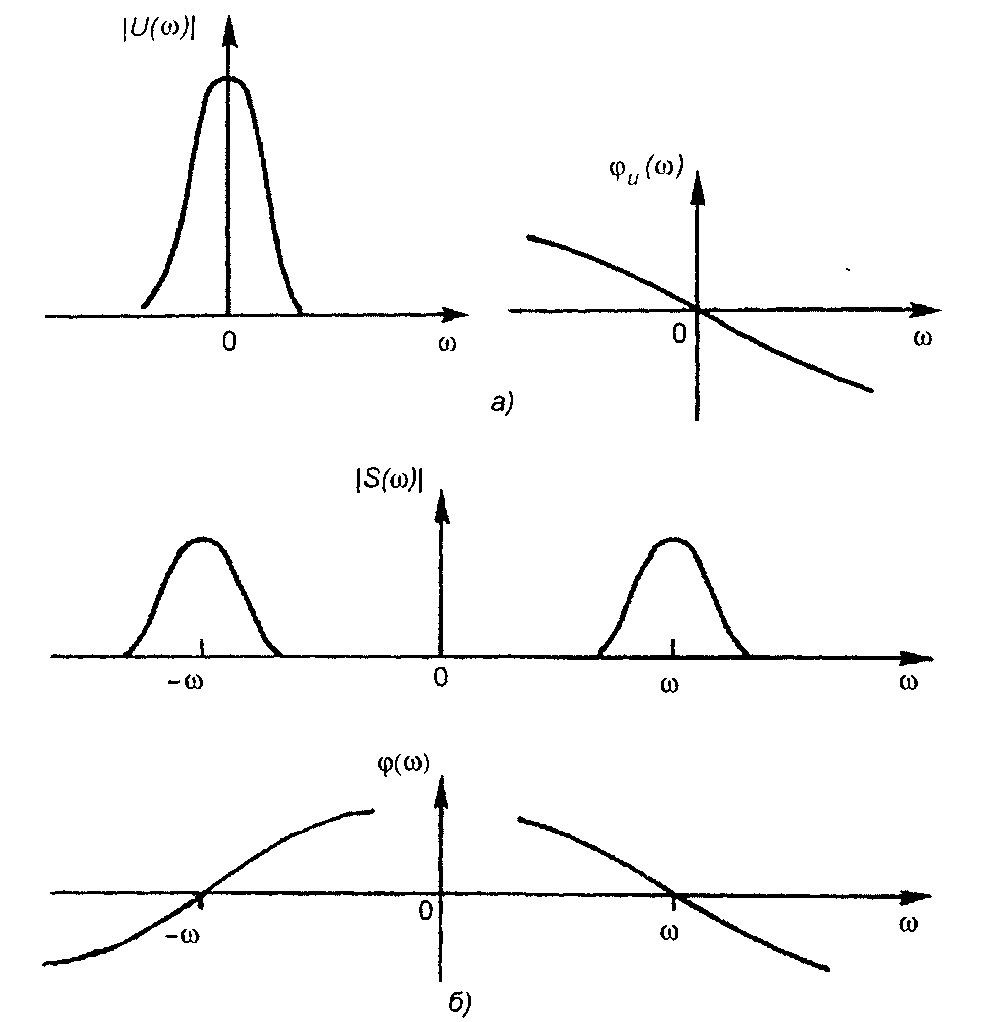
Рис. 8.2

2. Спектральной плотности комплексной огибающей сигнала (рис. 8.4,а)

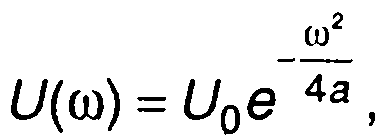
где а - параметр зависимости,

соответствует спектральная плотность сигнала (ω>0), рис. 8.4,6,

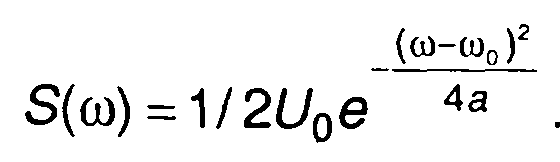
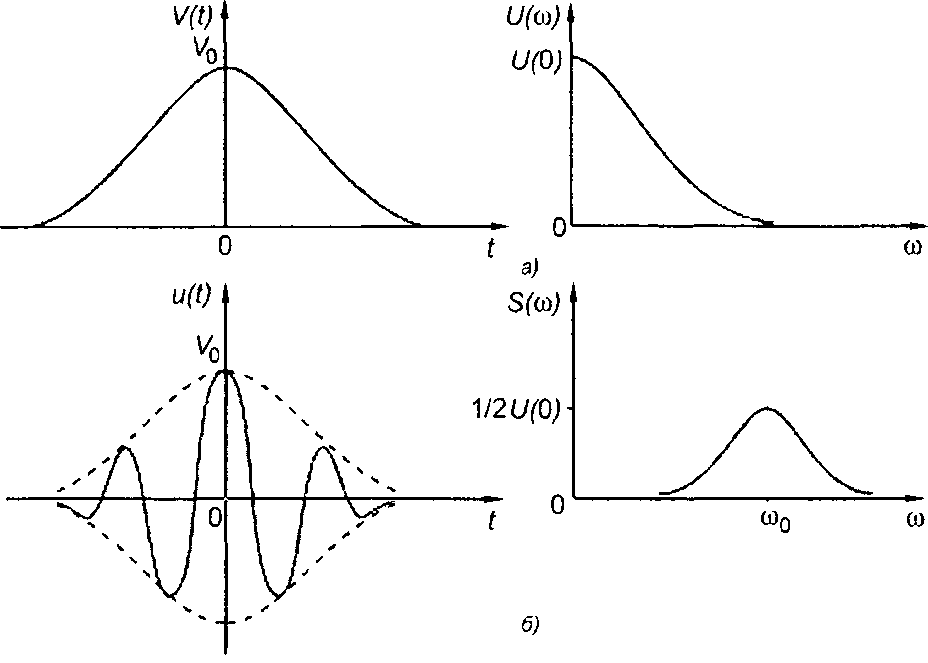
Рис. 8.3

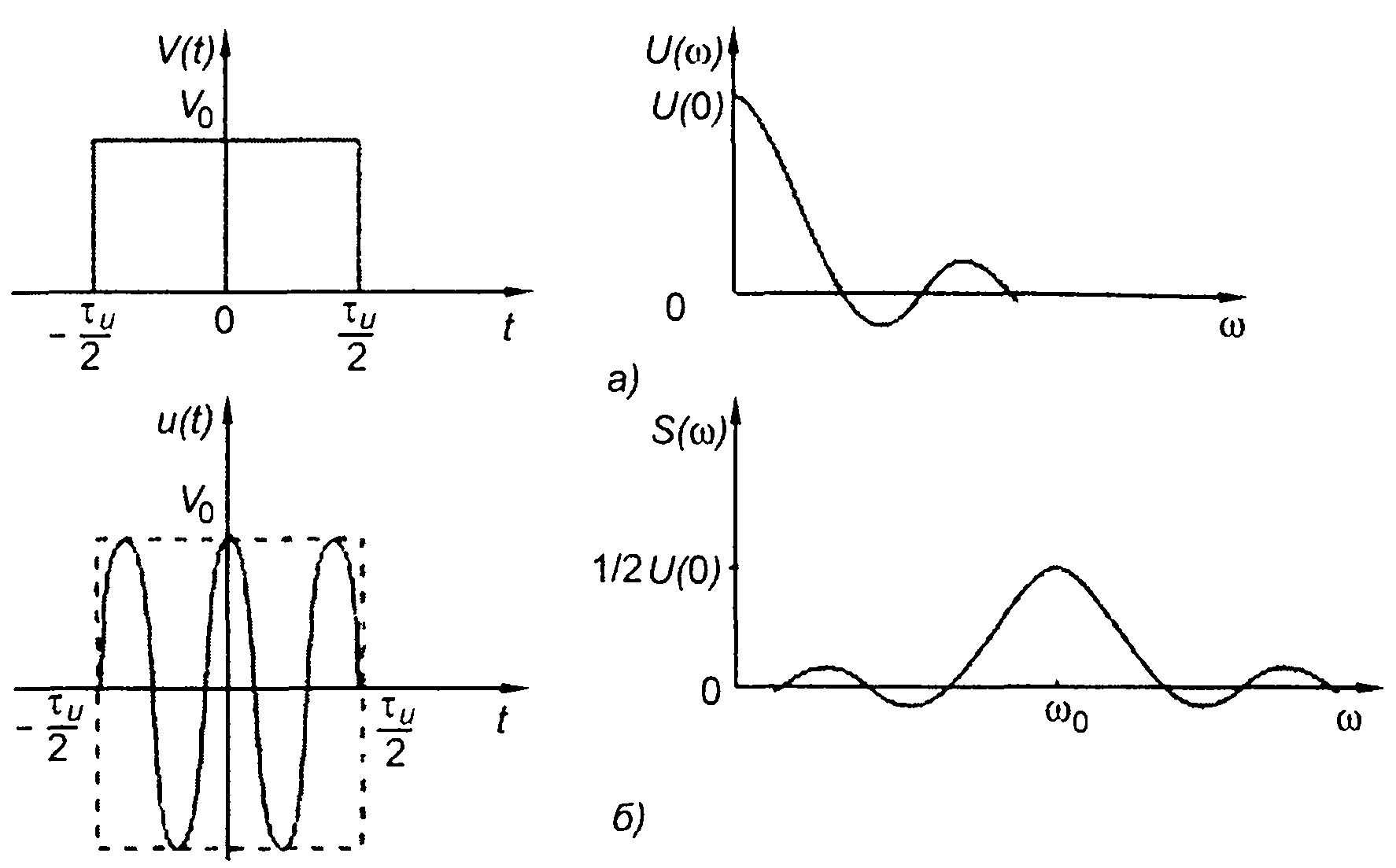
Рис. 8.4

8.4. Корреляционные функции узкополосных сигналов

Автокорреляционная функция сигнала определяется выражением

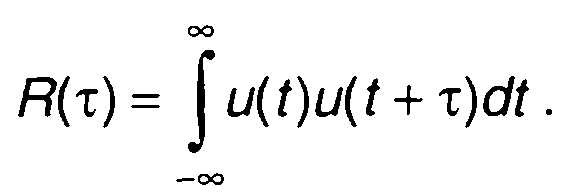(8.20)

Для узкополосного сигнала

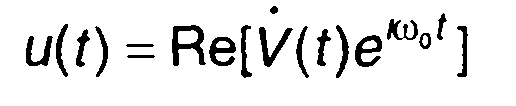(8.21)

с учетом (8.11) из (8.20) получим

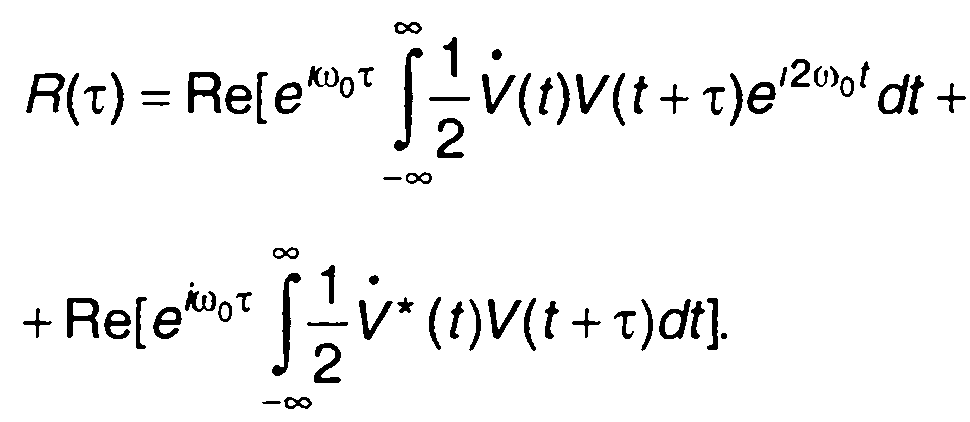(8.22)

Функция V(t) является низкочастотной, медленно меняется в течение периода несущего колебания 2π/ω₀. Вследствие этого зна­чение первого интеграла в (8.22) может быть принято равным нулю. Таким образом, выражение для автокорреляционной функции узко­полосного сигнала запишется в виде

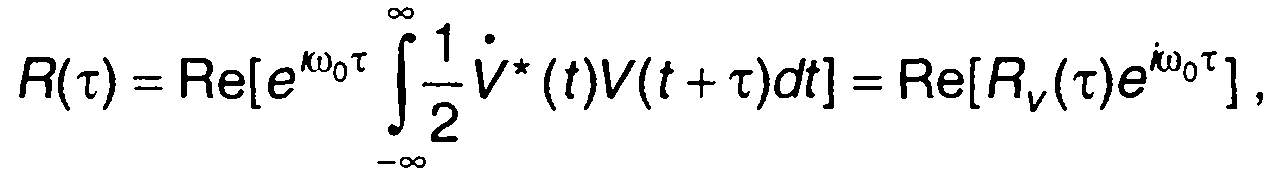(8.23)

где

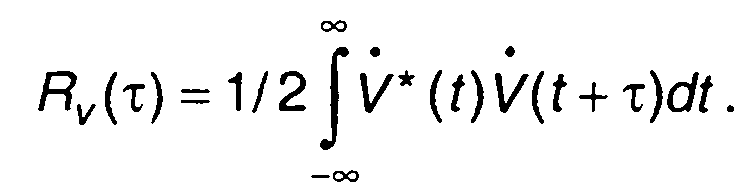(8.24)

Величина R_v(τ) представляет автокорреляционную функцию комплексной огибающей сигнала. Так как V(t) является комплекс­ной величиной, то в общем случае R_v(τ) представляет комплексную функцию. Автокорреляционная функция узкополосного сигнала R(x) является действительной. Соотношение, связывающее ее с авто­корреляционной функцией комплексной огибающей (8.23), анало­гично тому, которое связывает узкополосный сигнал с его ком­плексной огибающей. Часто целесообразно сначала определить

автокорреляционную функцию комплексной огибающей сигнала, а затем перейти к корреляционной функции узкополосного сигнала.

Примеры.

1. Корреляционной функции комплексной огибающей сигнала (рис.8.5)

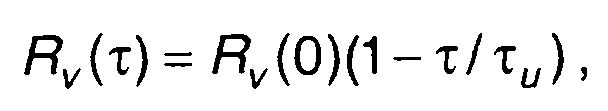
где τ_и - длительность сигнала,

соответствует корреляционная функция узкополосного сигнала (τ > 0)

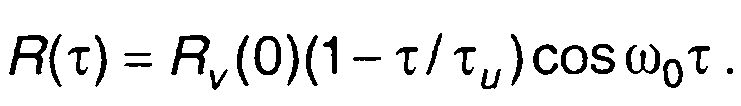
2. Корреляционной функции комплексной огибающей сигнал (рис.8.6)

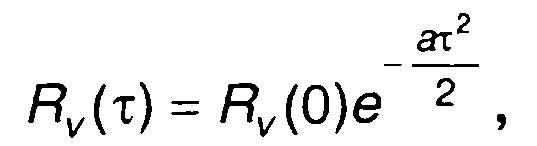
где а - параметр зависимости, соответствует корреляционная функция узкополосного сигнала

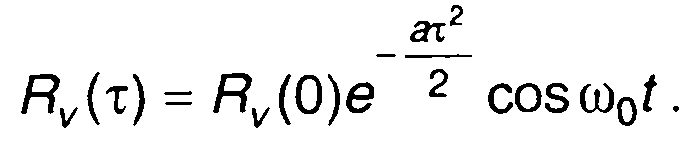
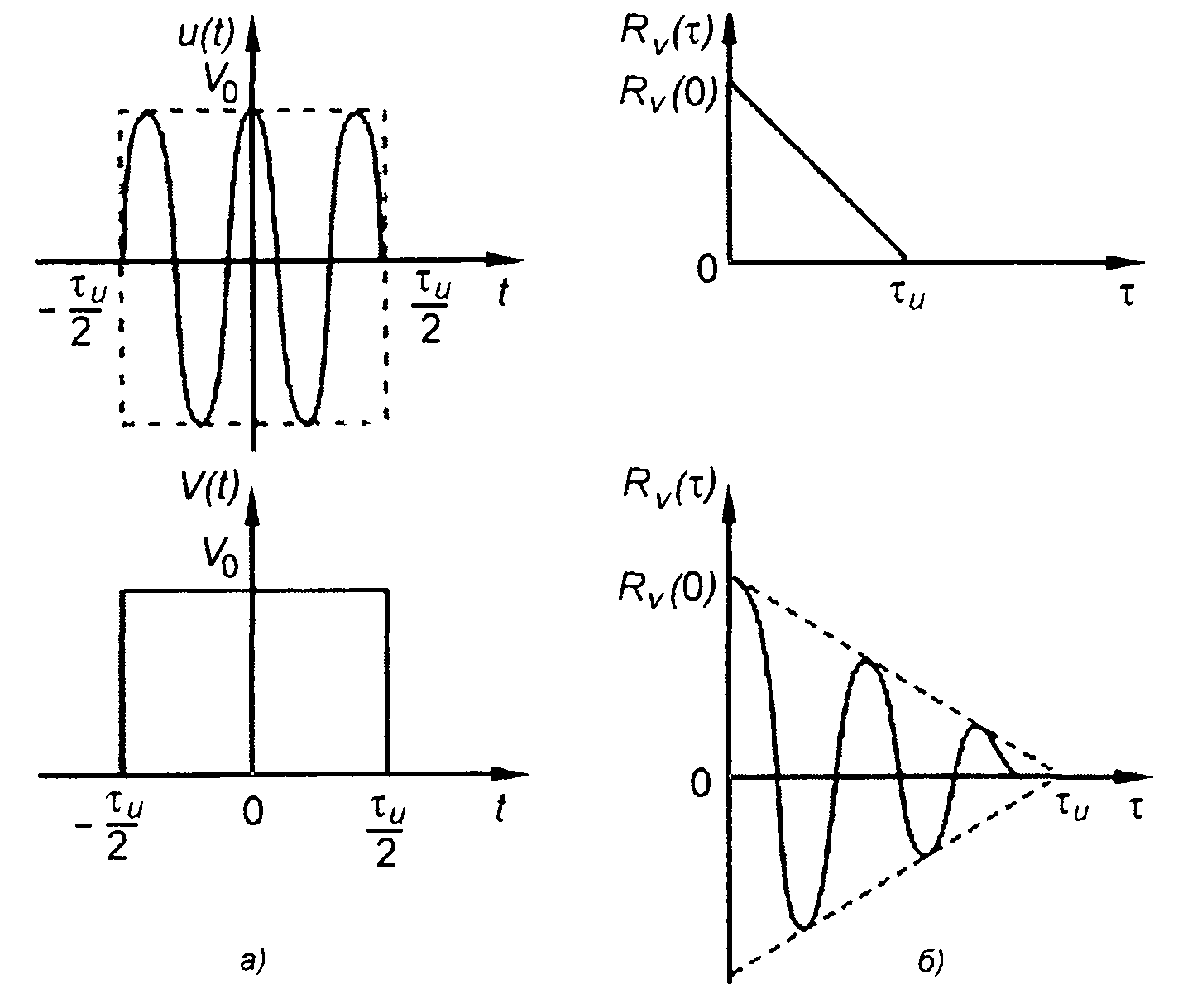
Рис. 8.5

Раздел 8

Рис.8.6

Взаимная корреляционная функция двух узкополосных сигналов, имеющих одинаковую несущую частоту ωо,

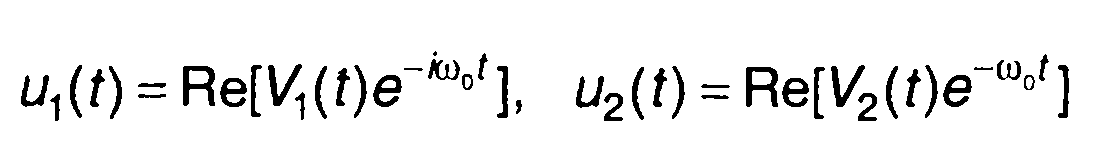(8.25)

определяется выражением

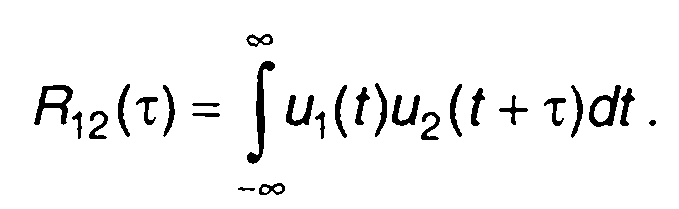(8.26)

Подставляя (8.25) в (8.26), с учетом (8.11) получаем

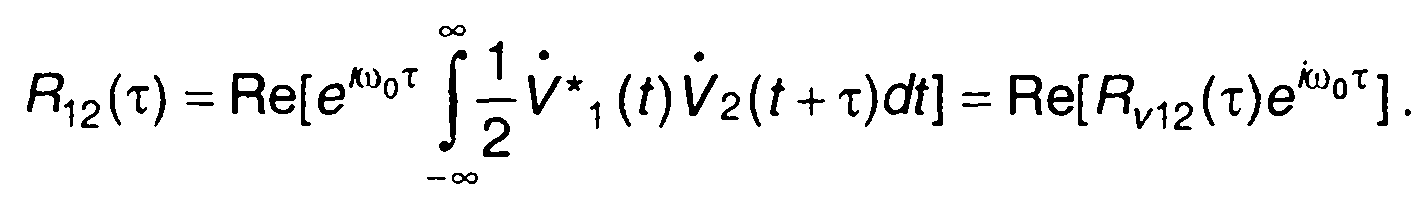(8.27)

В (8.27) величина

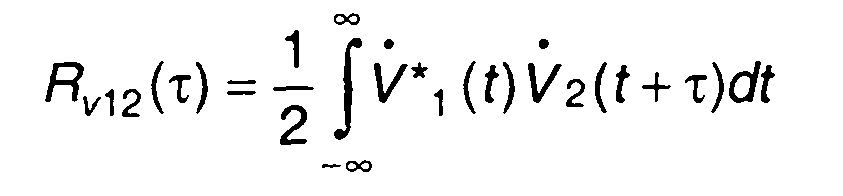(8.28)

представляет взаимную корреляционную функцию комплексных огибающих сигналов. Соотношение, связывающее ее с взаимной корреляционной функцией рассматриваемых узкополосных сигна­лов, имеет вид, аналогичный (8.23)

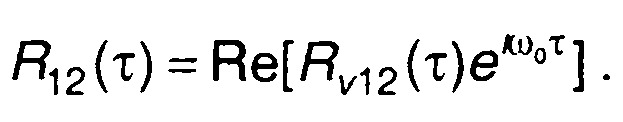(8.29)

При использовании свойства преобразования Фурье, можно по­лучить соотношение, связывающее автокорреляционную функцию комплексной огибающей сигнала R_v(τ) со спектральной плотностью энергии W_v(ω)

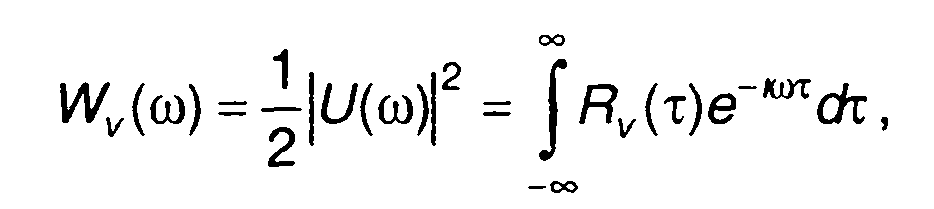(8.30)

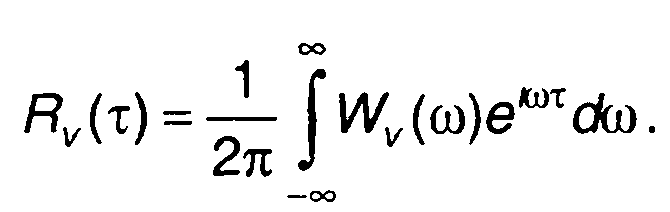(8.31)

При τ = 0 имеем

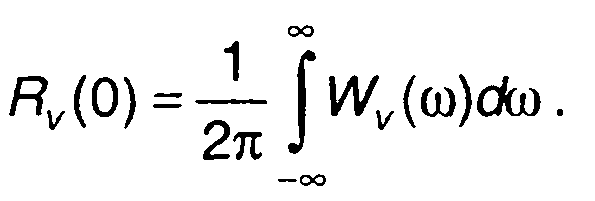(8.32)

С учетом (8.24) и (8.32) можем записать

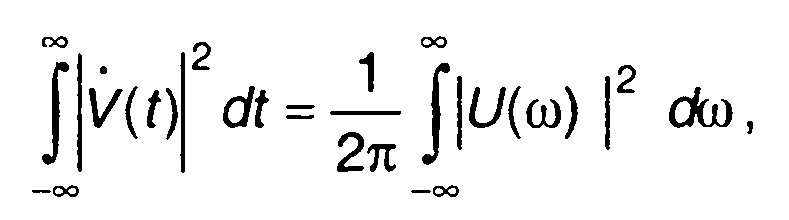(8.33)

что представляет равенство Парсеваля для комплексных огибаю­щих узкополосных сигналов.

Выражение для спектральной плотности энергии узкополосного сигнала запишем в виде

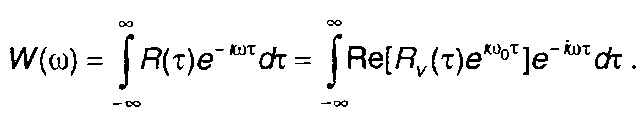(8.34)

Из (8.34) аналогично (8.17) получим

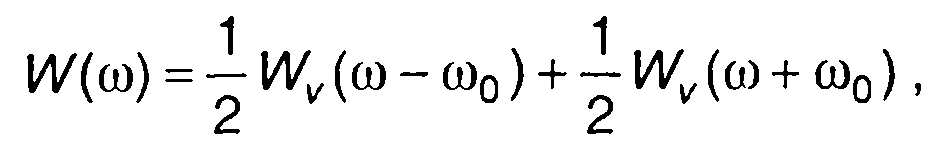(8.35)

где W_v(ω}~ спектральная плотность энергии комплексной огибаю­щей

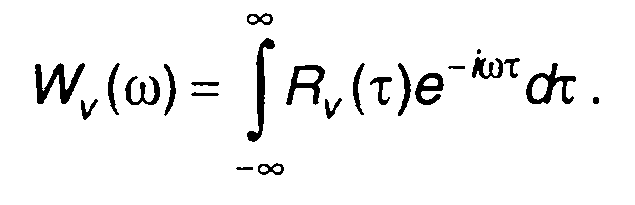(8.36)

Спектральная плотность энергии комплексной огибающей явля­ется действительной величиной, поэтому в (8.35) отсутствует обо­значение комплексно сопряженной величины второго слагаемого. Как следует из (8.36), спектральная плотность энергии узкополосно­го сигнала имеет две составляющие - в области положительных частот 1/2W_v(ω-ω₀) и отрицательных частот 1/2W_v(ω-ω₀) .

Соотношения, аналогичные (8.30) и (8.31), связывают взаимную корреляционную функцию с взаимной спектральной плотностью энергии комплексных огибающих узкополосных сигналов

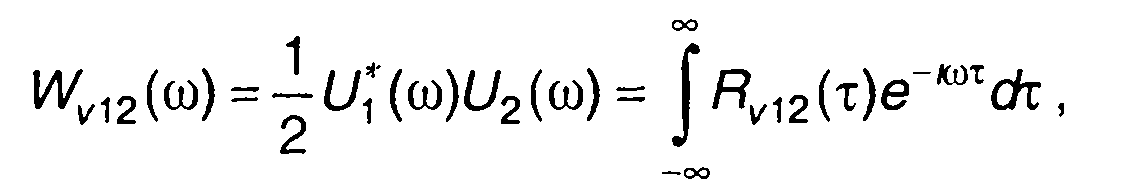(8.37)

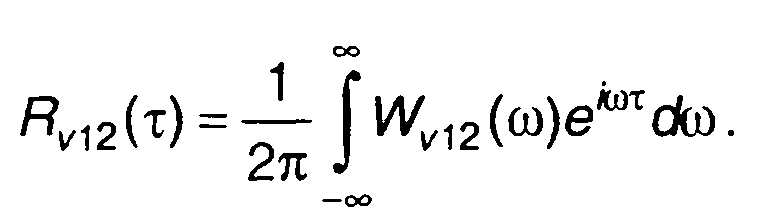(8.38)

8.5. Аналитичесий сигнал

При анализе узкополосных сигналов в ряде случаев пользуются понятием аналитического сигнала. Аналитический сигнал опреде­ляется как

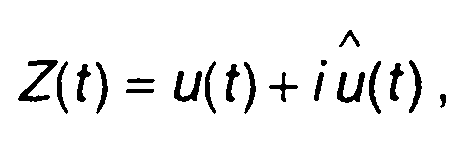(8.39)

где u(t) - узкополосный сигнал, описываемый (8.1); u(t)- сигнал, сопряженный с u(t) по Гильберту

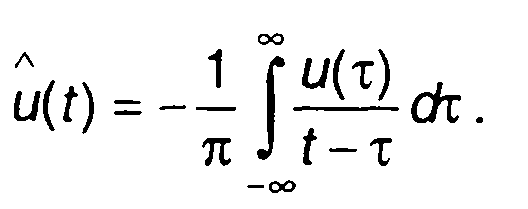(8.40)

Аналитический сигнал, как комплексная величина, определяется модулем IZ(t)l и аргументом φ_z(t)

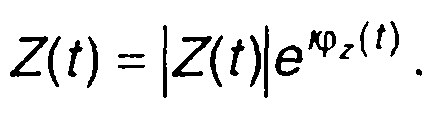(8.41)

Для сигнала

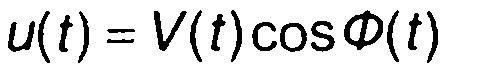(8.42)

сопряженный сигнал, определяемый (8.40), равен

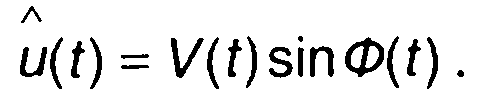(8.43)

С учетом (8.42) и (8.43) выражение для аналитического сигнала (8.39) получим в виде

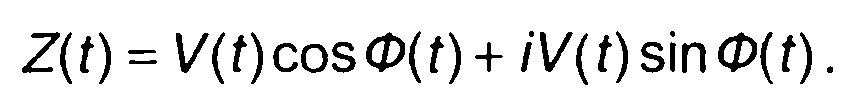(8.44)

Модуль аналитического сигнала равен огибающей узкополосного сигнала

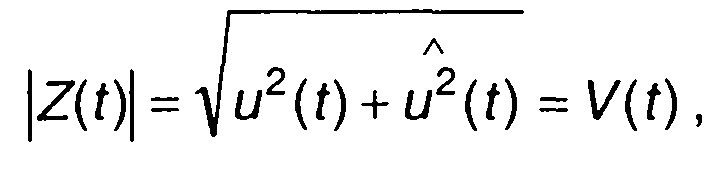(8.45)

а аргумент фазе

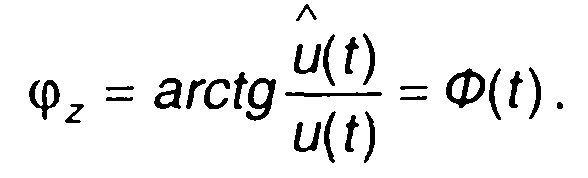(8.46)

С учетом (8.45) и (8.46) выражение (8.41) можем записать в виде

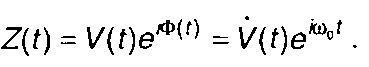(8.47)

Таким образом, аналитический сигнал представляет комплекс­ный сигнал, введенный при описании узкополосного сигнала (8.2).

8.6. Обобщенная корреляционная функция сигнала

Для характеристики точности и разрешающей способности ра­диолокационных систем используется обобщенная корреляционная функция. Она определяется как корреляционная функция ком­плексных огибающих узкополосных сигналов с различной частотой (как правило, без коэффициента 1/2).

Комплексные огибающие узкополосных сигналов u₁(t) и u₂(t), от­личающихся только сдвигом несущей частоты Ω, при Ω<<ω₀, пред­ставим в виде

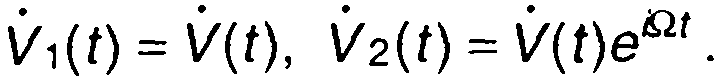(8.48)

С учетом (8.48) от определения взаимной корреляционной функции комплексных огибающих узкополосных сигналов перейдем к выражению для обобщенной корреляционной функции

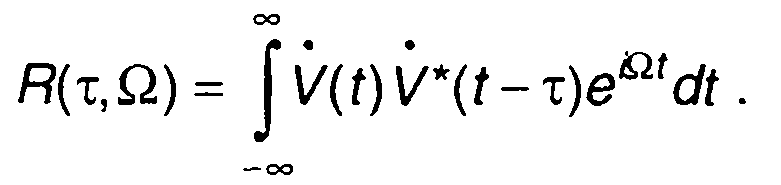(8.49)

Функция R(τ,Ω) связана со спектральными плотностями огибаю­щих сигналов соотношением

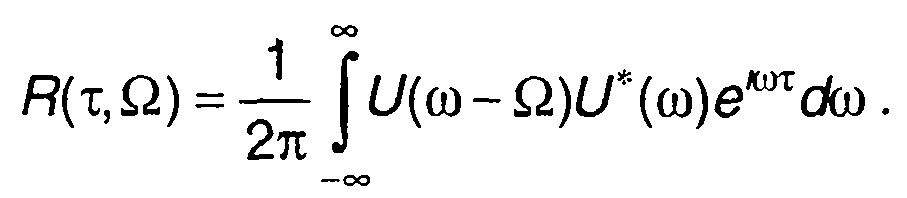(8.50)

Функция R(τ, Ω) характеризует разрешающую способность сис­темы, в которой используется рассматриваемый сигнал, поэтому ее называют также функцией неопределенности.

При Ω = 0 имеем

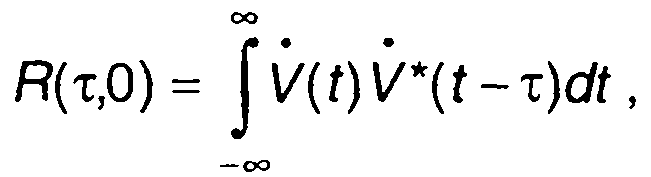(8.51)

или

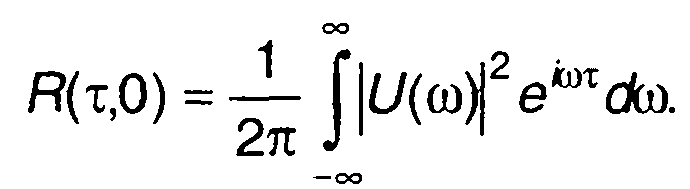(8.52)

Функция R(τ, 0) является функцией неопределенности по даль­ности. Она равна удвоенной величине автокорреляционной функ­ции комплексной огибающей сигнала. Максимальное значение по­лучается при τ = 0. Чем больше значение \R(t, 0)\ отличается от \R(0, 0)\, тем легче могут быть различены две цели, отличающиеся запаздыванием отраженного сигнала т. Обычно разрешение целей характеризуется квадратом функции неопределенности \R(τ,Ω)\². Постоянная разрешения по запаздыванию определяется как

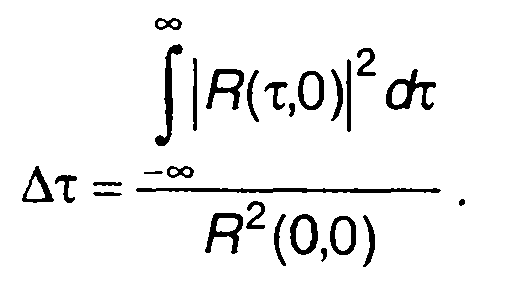(8.53)

Используя спектральную плотность комплексной огибающей сигнала и учитывая равенство Парсеваля, (8.53) можем записать в виде

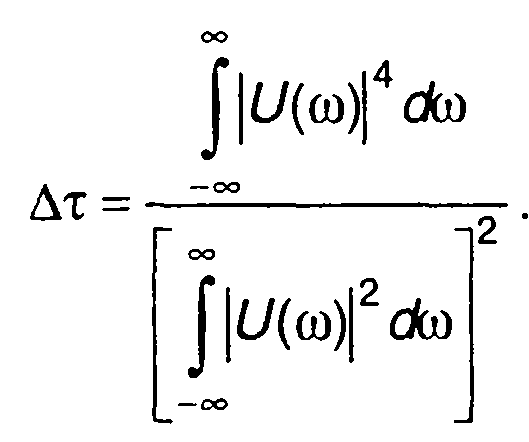(8.54)

При х =0 функция неопределенности равна

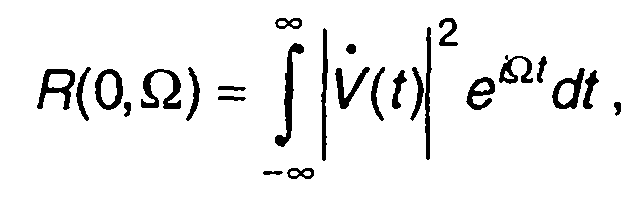(8.55)

или

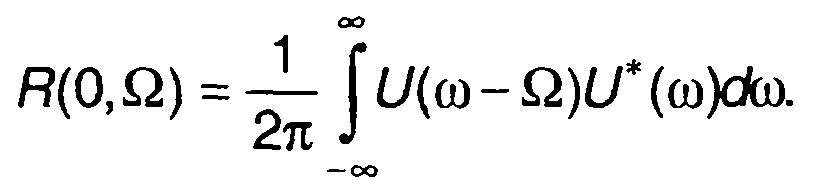(8.56)

Постоянная разрешения по частоте определяется аналогично постоянной разрешения по запаздыванию

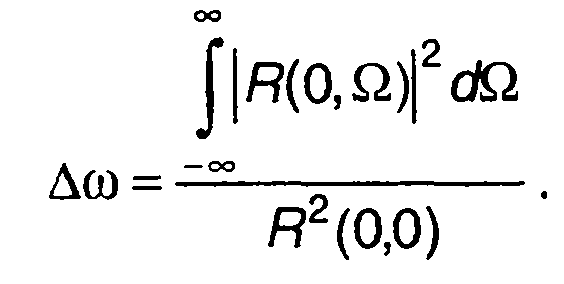(8.57)

Функция неопределенности дает возможность оценить степень различения сигналов, отличающихся значениями запаздывания τ и частоты Чем ближе |R(τ, Ω)| по значению к |R(0,0)|, тем труднее различаются сигналы, отличающиеся запаздыванием х и частотой Ω.

Мерой совместной разрешающей способности по запаздыванию и частоте может служить эффективная площадь неопределенности

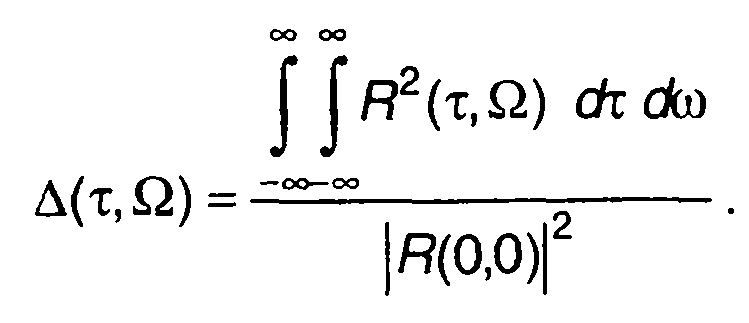(8.58)

В качестве примеров рассмотрим функции неопределенности некоторых видов сигналов.

1. Сигнал с прямоугольной огибающей и постоянной частотой. 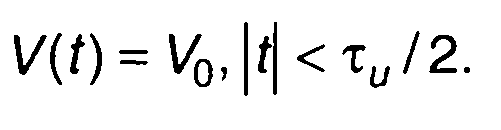Выражение для функции неопределенности имеет вид:

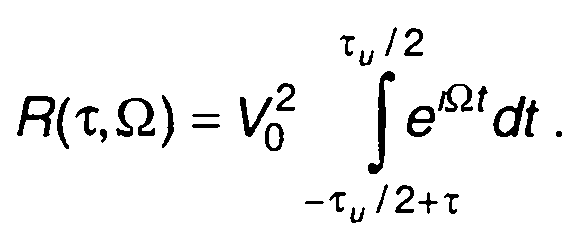
Из него получим

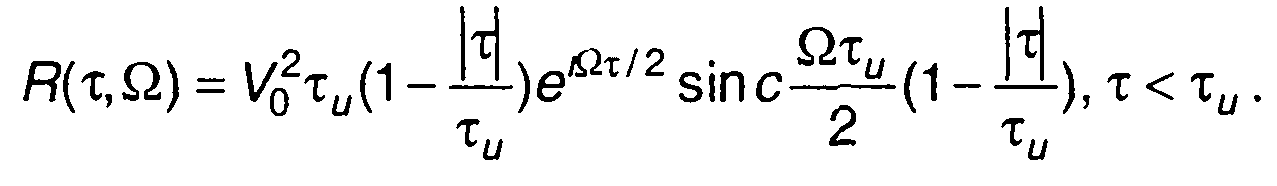
Модуль функции неопределенности

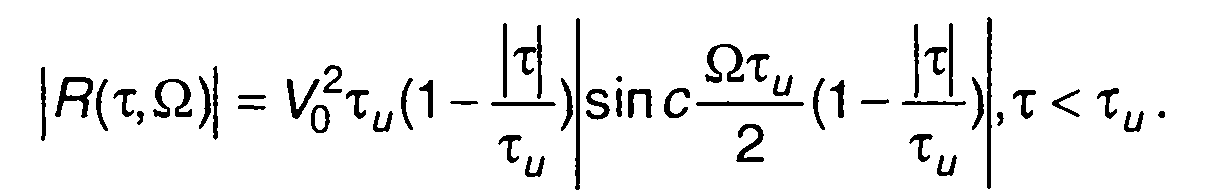
При Ω = 0 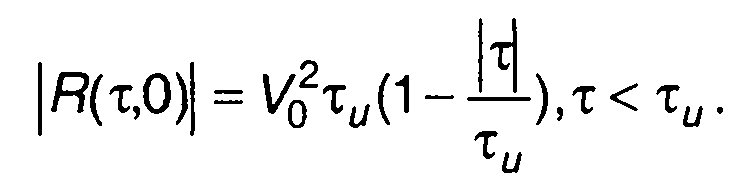При т = 0

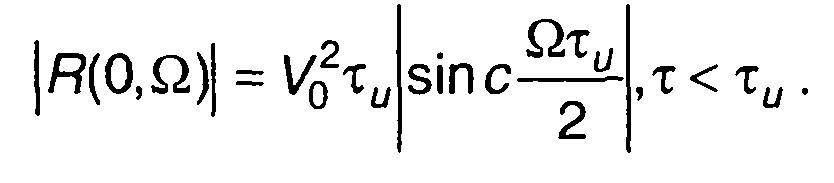
2. Сигнал с прямоугольной огибающей и линейно изменяющейся частотой (разд. 11)

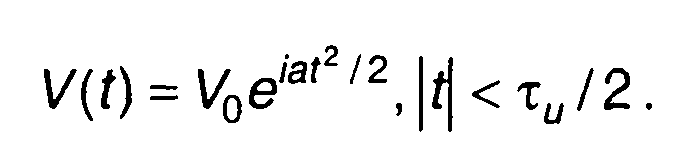
Функция неопределенности описывается выражением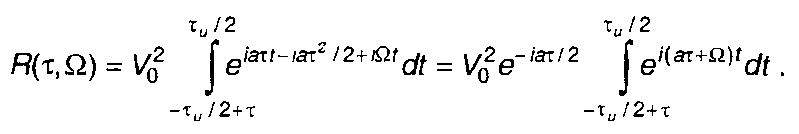

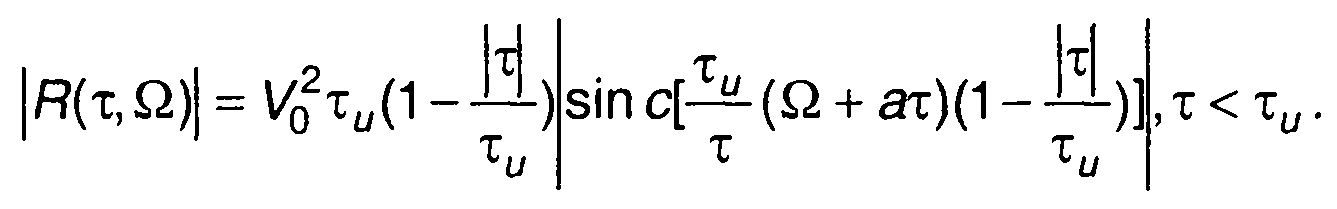
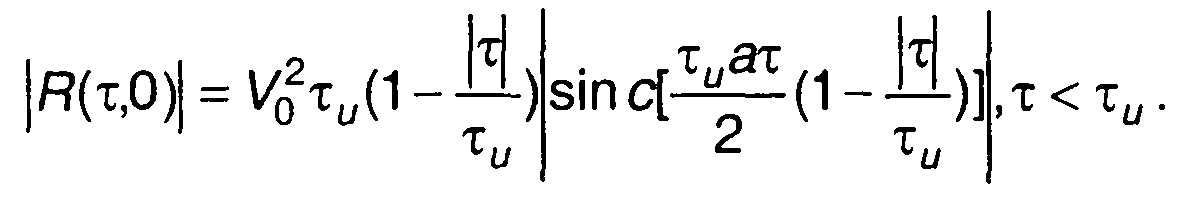
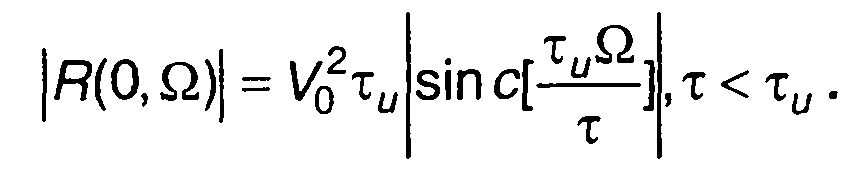
Из записанного выражения получим 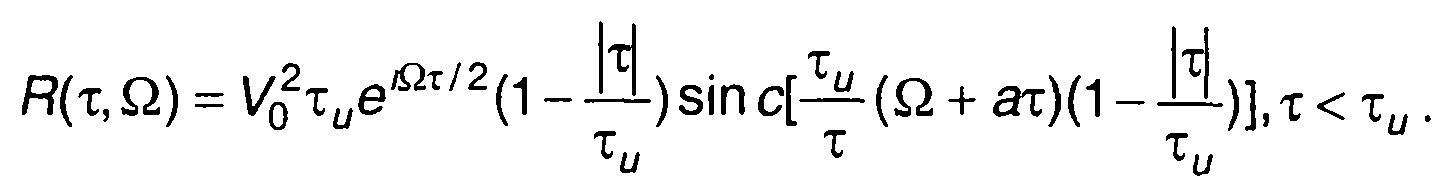Модуль функции неопределенности

При Ω = О При τ = О

8.7. Дискретизация узкополосного сигнала

Принципы дискретизации непрерывного сигнала могут быть рас­пространены на узкополосный сигнал

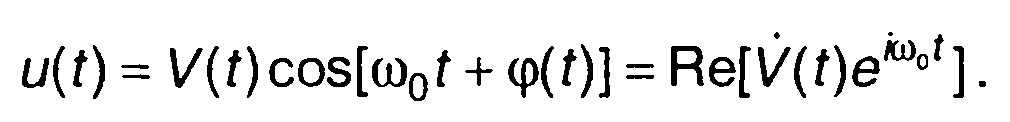(8.59)

Комплексная огибающая V(t), имеющая спектр, ограниченный частотой ∆ω/2 (рис.8.7), может быть представлена рядом Котель­никова

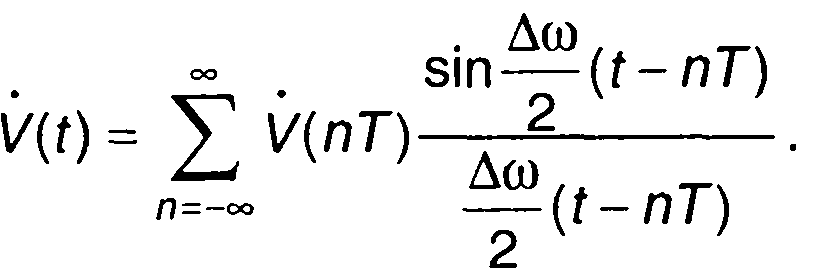(8.60)

Коэффициенты ряда определяются как

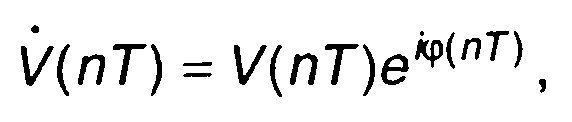(8.61)

период дискретизации выбирается из соотношения

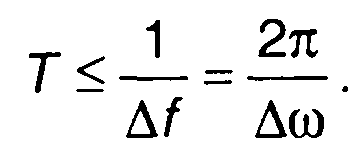(8.62)

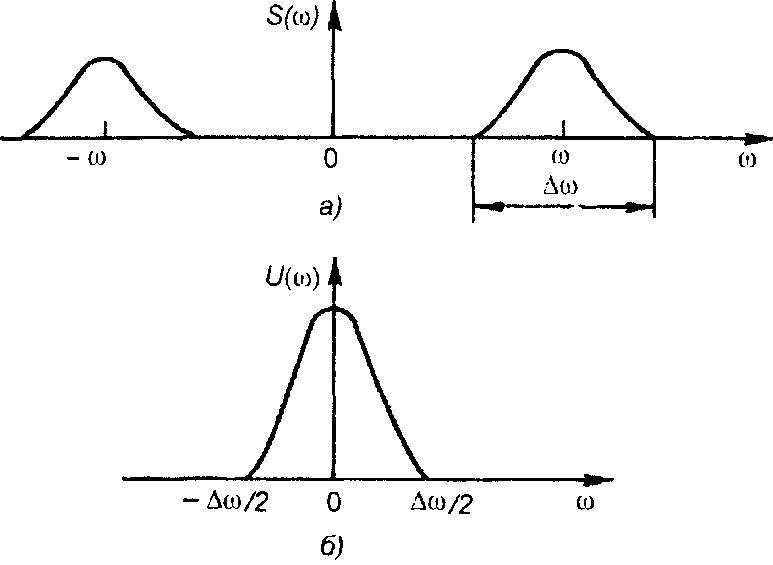
Рис. 8.7

С учетом (8.60) и (8.61) выражение для узкополосного сигнала запишем в виде

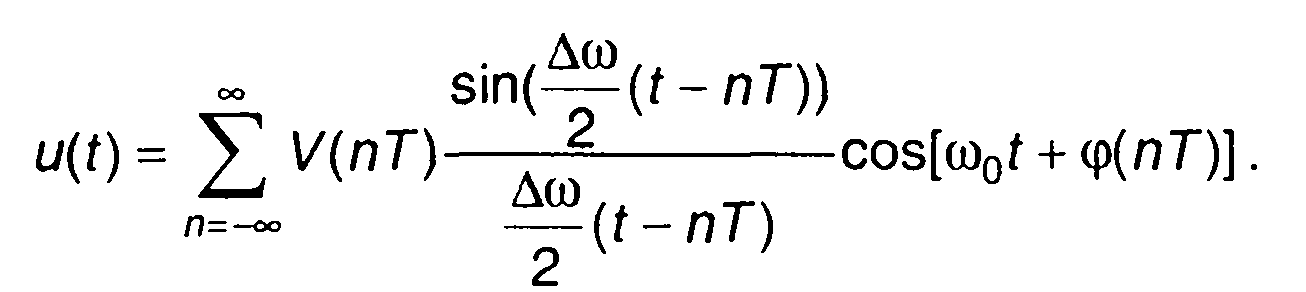(8.63)

Выражение (8.64) представляет ряд Котельникова для узкопо­лосного сигнала. Он описывает сигнал, спектр которого заключен в ограниченной полосе частот ∆ω. Ряд Котельникова для узкопо­лосного сигнала включает слагаемые, которые имеют вид моду­лированных колебаний с несущей частотой ω_о, фазой φ(пТ) и оги­бающей

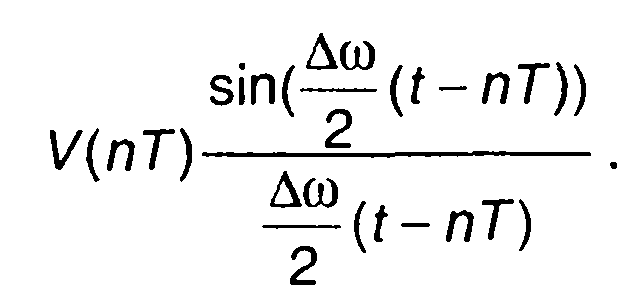(8.64)

Если длительность сигнала равна Т_с, то число интервалов раз­биения равно N =Т_С/Т. Таким образом, ряд Котельникова для узко­полосного сигнала можем записать в виде

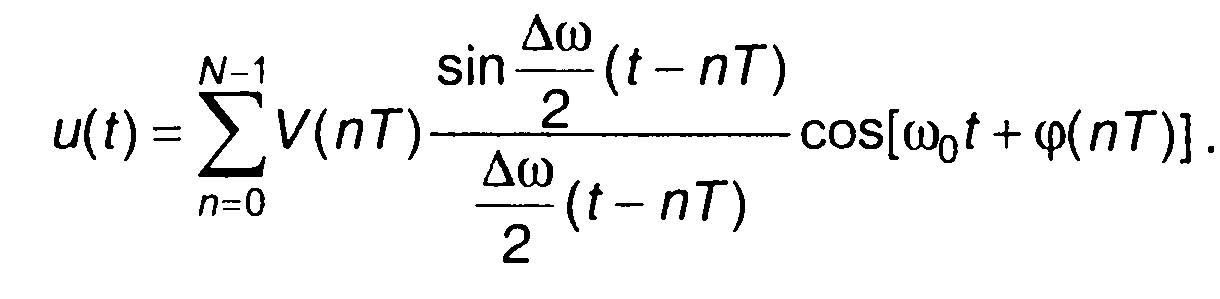(8.65)

Выборочные значения сигнала задаются двумя параметрами V(nτ) и φ(nτ)

8.8. Модулированные сигналы

Узкополосными сигналами чаще всего являются модулирован­ные колебания. Модулированные колебания представляют высоко­частотные колебания, на которые накладываются низкочастотные, несущие информацию. Выбор несущей частоты высокочастотного колебания производится исходя из условий распространения ра­диоволн, приема их антеннами и ряда других факторов. Переда­ваемая информация содержится в сигнале, накладываемом на вы­сокочастотное колебание. Наибольшая частота спектра сигнала, содержащего информацию, должна быть значительно меньше не­сущей частоты. Процесс наложения сигнала, содержащего инфор­мацию, на высокочастотное колебание называется модуляцией. Сигнал, содержащий передаваемую информацию, называется мо­дулирующим. Модулируется несущее колебание путем изменения одного или нескольких параметров. Наиболее часто несущим коле­банием является гармоническое. Однако могут использоваться и другие виды колебаний, например, периодическая последователь­ность импульсов или шум. Гармоническое колебание можно моду­лировать по амплитуде, фазе или частоте. Модуляция по фазе или частоте носит название угловой модуляции. В дальнейшем рас­сматриваются гармонические колебания с различными видами мо­дулями.

Раздел 9.

АМПЛИТУДНО-МОДУЛИРОВАННЫЕ СИГНАЛЫ

При амплитудной модуляции (AM) под воздействием модули­рующего (управляющего) сигнала, несущего информацию, изменя­ется амплитуда сигнала. Как правило, AM сигнал является узкопо­лосным, относительное изменение амплитуды за один период не­сущего колебания мало. Такие сигналы, узкополосные амплитудно- модулированные, и рассматриваются в настоящем разделе.

9.1.Описание AM сигнала

Узкополосный AM сигнал с гармоническим несущим колебанием описывается выражением (рис. 9.1,а)

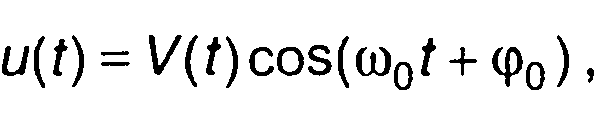(9.1)

где V(t) - амплитуда; ω₀,φ₀ -частота и начальная фаза несущего колебания.

Выражение для AM сигнала может быть записано также в ком­плексной форме

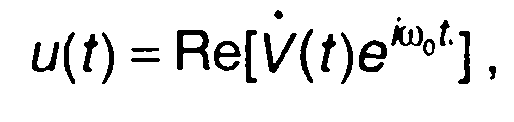(9.2)

где V(t) = V(t)e^iφ0 - комплексная огибающая сигнала; при φ₀=0

комплексная огибающая сигнала V(t) совпадает с амплитудой V (t).

Графически комплексный сигнал можно изобразить в виде век­тора на комплексной плоскости. Длина вектора равна V(t), изме­няется во времени (рис. 9.1,6). Угол между вектором и действи­тельной осью постоянен и равен φ₀. Система координат враща­ется по часовой стрелке с угловой скоростью ω₀. Проекция векто­ра на действительную ось в каждый момент времени описывает AM сигнал u(t).

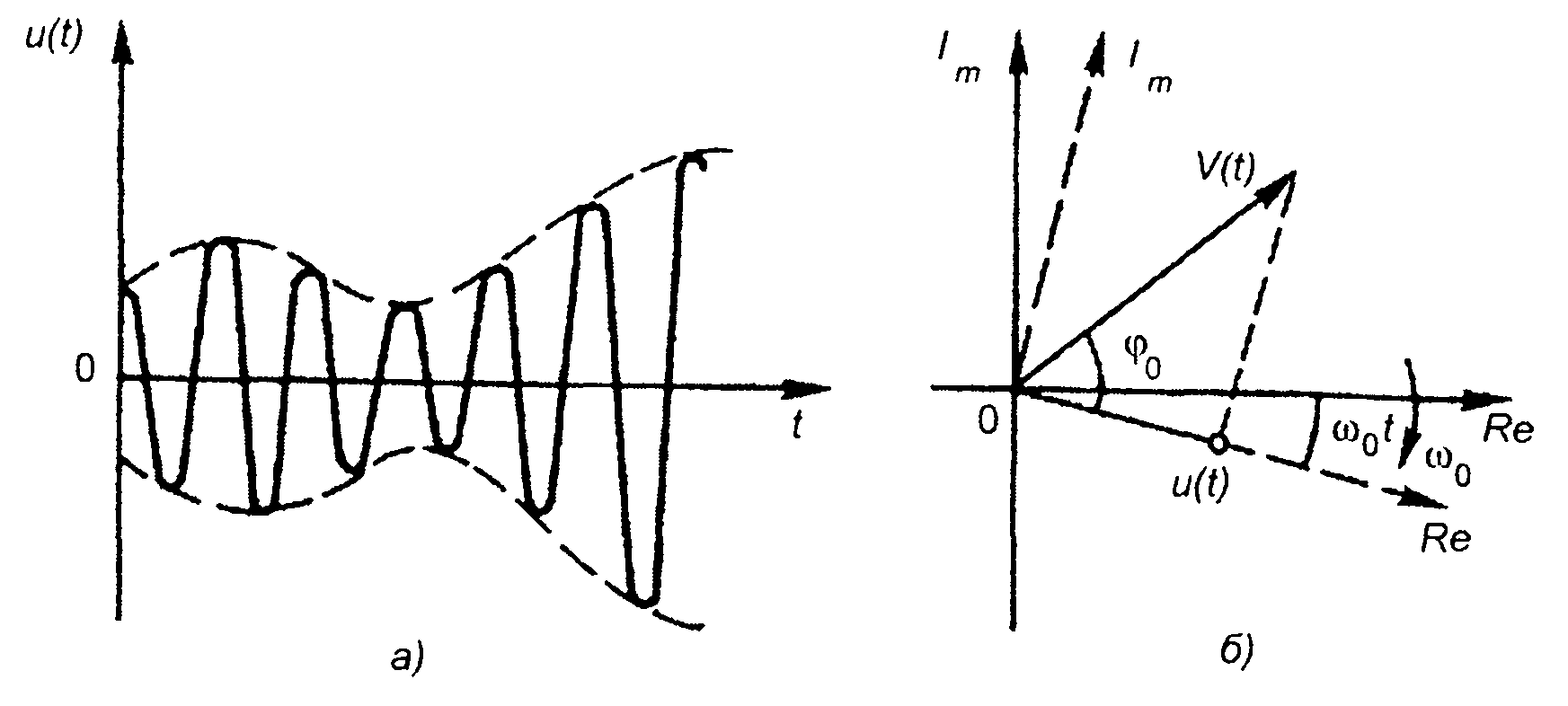
Рис. 9.1

9.2. Тональная амплитудная модуляция

При амплитудной модуляции амплитуда зависит от модулирую­щего сигнала s(t). Эта зависимость, как правило, линейная

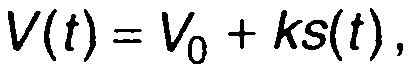(9.3)

где k- коэффициент пропорциональности.

Вид модулирующего сигнала определяет спектр AM сигнала. Простейший модулирующий сигнал - гармонический. При гармони­ческой или тональной модуляции AM сигнал описывается выраже­нием (рис. 9.2,а)

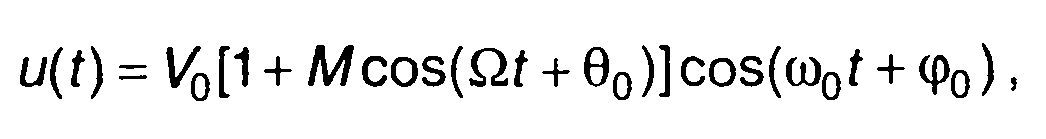(9.4)

где М = ks₀/V₀ - коэффициент модуляции, М < 1, Ω Θ_О – частота и начальная фаза гармонического модулирующего сигнала, Ω << ω₀.

Исходя из (9.4), AM сигнал можно представить в виде суммы гармонических составляющих и определить спектр тонально AM сигнала

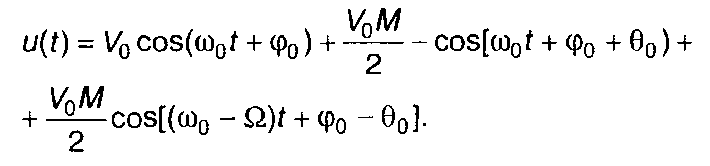(9.4)

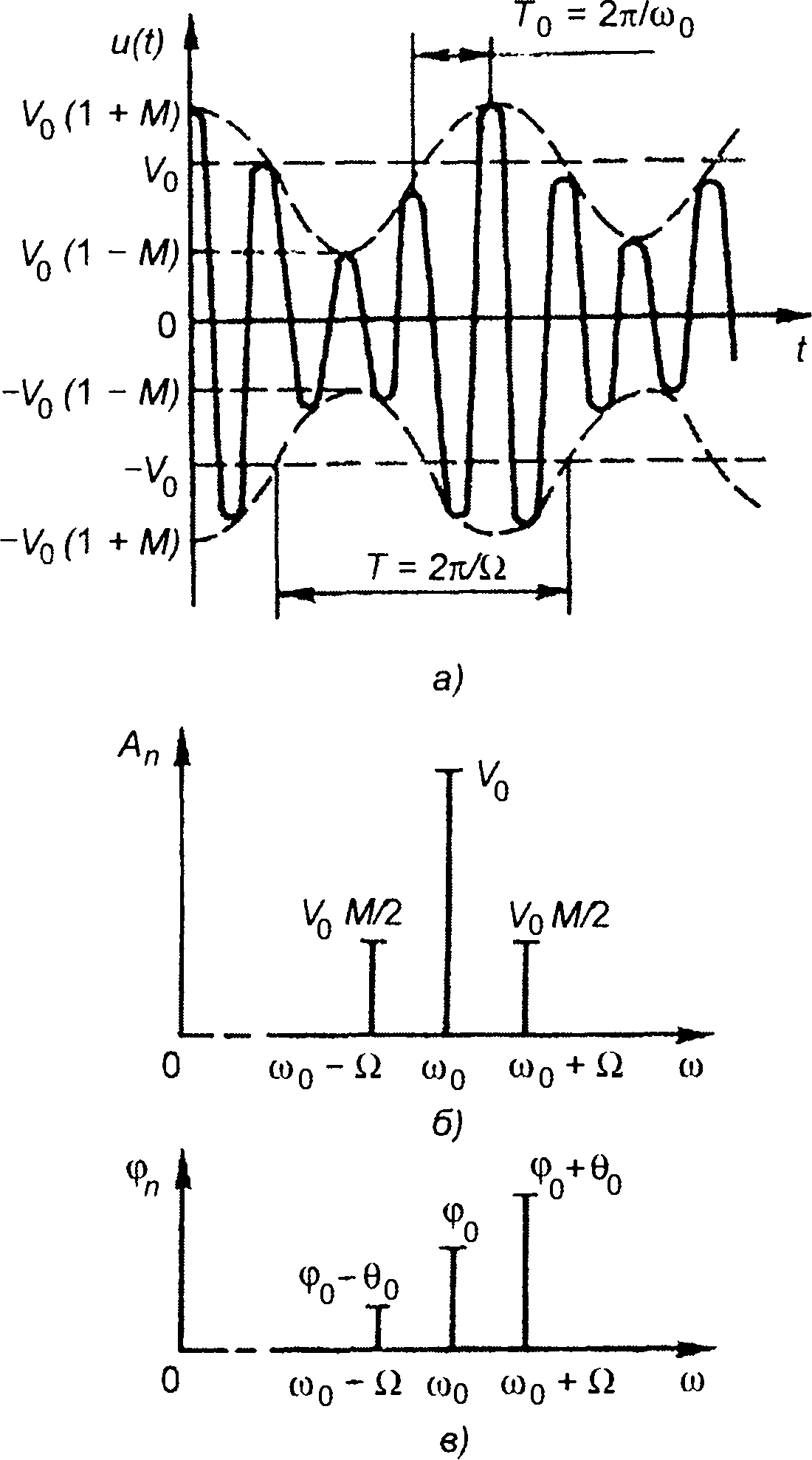
Рис. 9.2

Из (9.5) следует, что тонально AM сигнал включает три гармониче­ские составляющие: несущее колебание и два боковых с частотами AM сигнал включает три гармонические составляющие: несущее колеба­ние и два боковых с частотами Ω₀ ± Ω . Графики амплитудного и фа­зового спектров приведены на рис. 9.2,6,в. Амплитудный спектр имеет четную симметрию относительно несущей частоты, а фазо­вый - нечетную относительно начальной фазы. Ширина спектра равна удвоенной частоте модуляции 2Ω .

Средняя мощность тонально AM сигнала может быть определе­на из (9.5) как сумма средних мощностей спектральных состав­ляющих

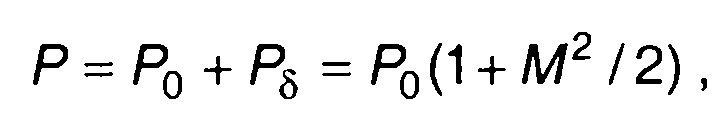(9.6)

где Р₀ - мощность несущего колебания; Р_δ - мощность боковых составляющих.

Мощность боковых составляющих Р_δ равна M²/2 от мощности несущего колебания Р₀.

9.3. Многотональная амплитудная модуляция

Модулирующий сигнал, как правило, имеет сложный спектраль­ный состав (рис. 9.3). В этом случае AM сигнал можно записать в виде

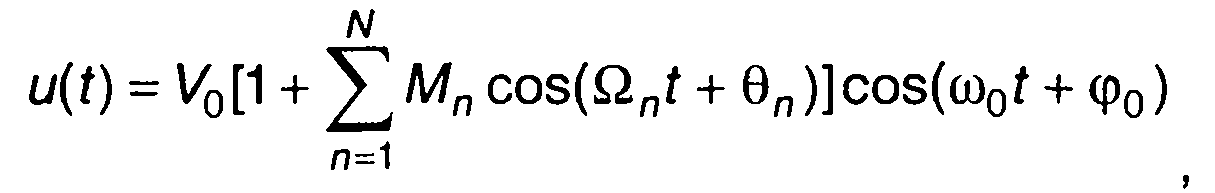(9.7)

где Ω_n,Θ_n - частоты модуляции (Ω₁<Ω₂<...<Ω_n <<ω₀) и началь­ные фазы составляющих модулирующего сигнала;

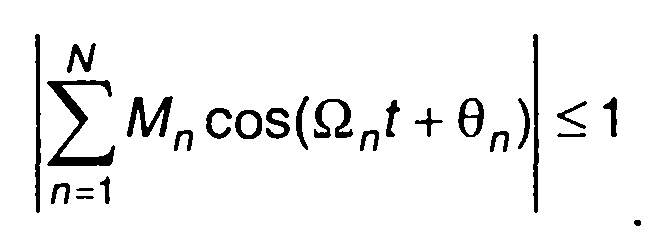(9.8)

Из (9.7) после преобразования получим представление сигнала в виде суммы гармонических составляющих

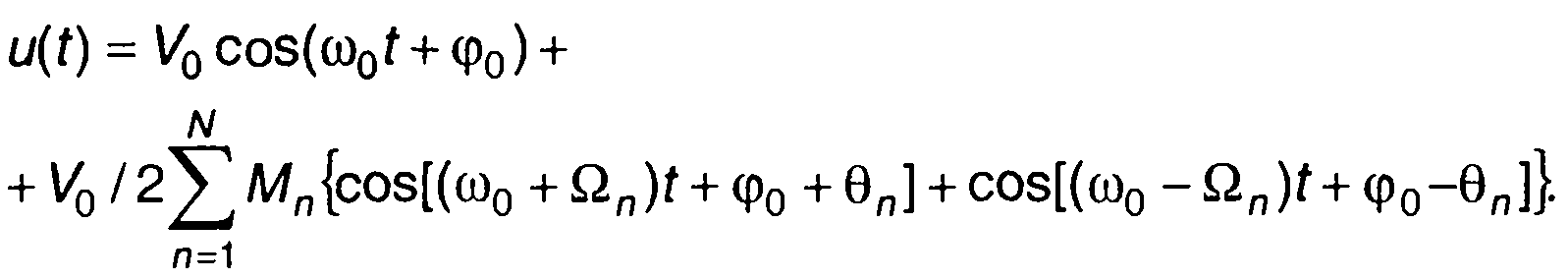(9.9)

Анализ (9.9) показывает, что при многотональной модуляции AM сигнал содержит несущее колебание и полосы верхних и нижних боковых составляющих. Амплитудный спектр сигнала имеет четную симметрию относительно ω₀ , фазовый - нечетную симметрию, от­носительно φ₀ (рис. 9.4). Ширина спектра AM сигнала равна удво­енной максимальной частоте модуляции

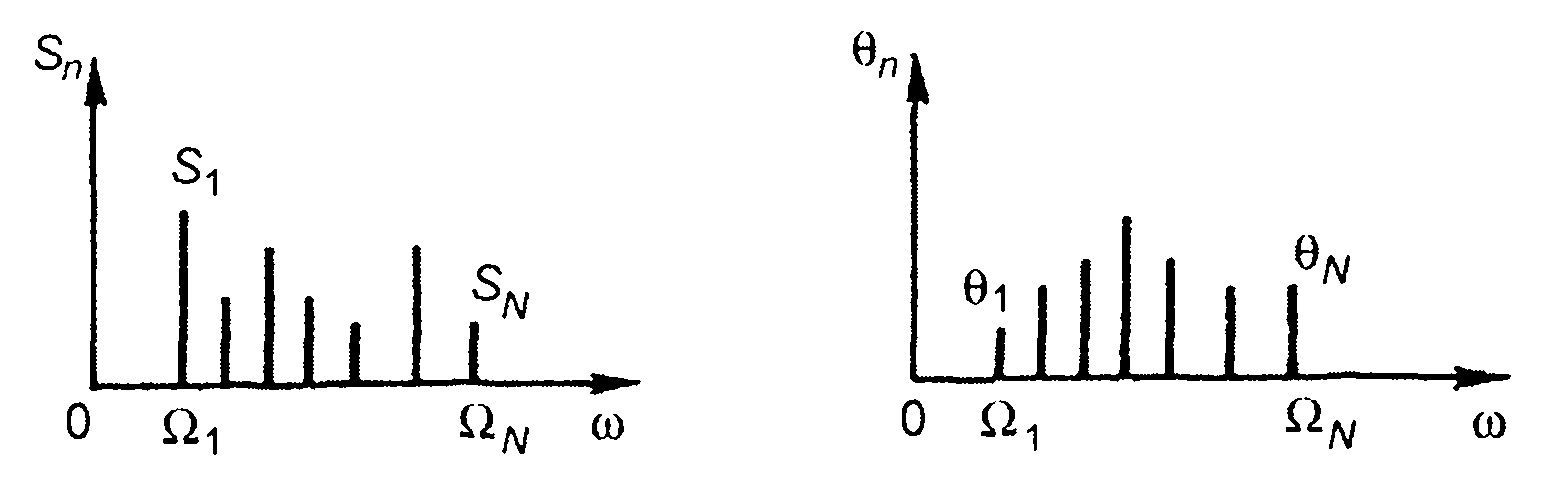
Рис. 9.3

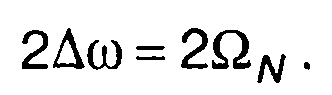(9.10)

Выражение (9.9) и график спектра, приведенный на рис.9.4, по­казывают, что спектр модулирующего сигнала полностью отобра­жается в боковой полосе спектра AM сигнала. Боковые полосы яв­ляются зеркальными копиями одна другой. Это свидетельствует об избыточности передачи информации двумя боковыми полосами.

Средняя мощность AM сигнала при многотональной модуляции определяется из (9.9) как сумма средних мощностей несущего ко­лебания и боковых составляющих

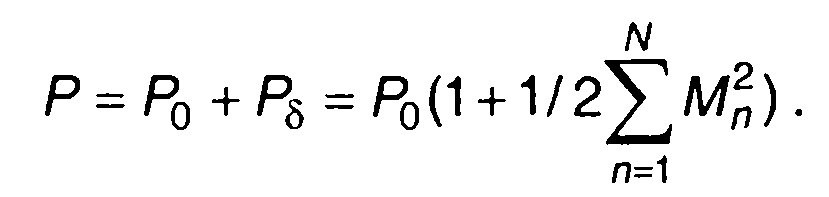(9.11)

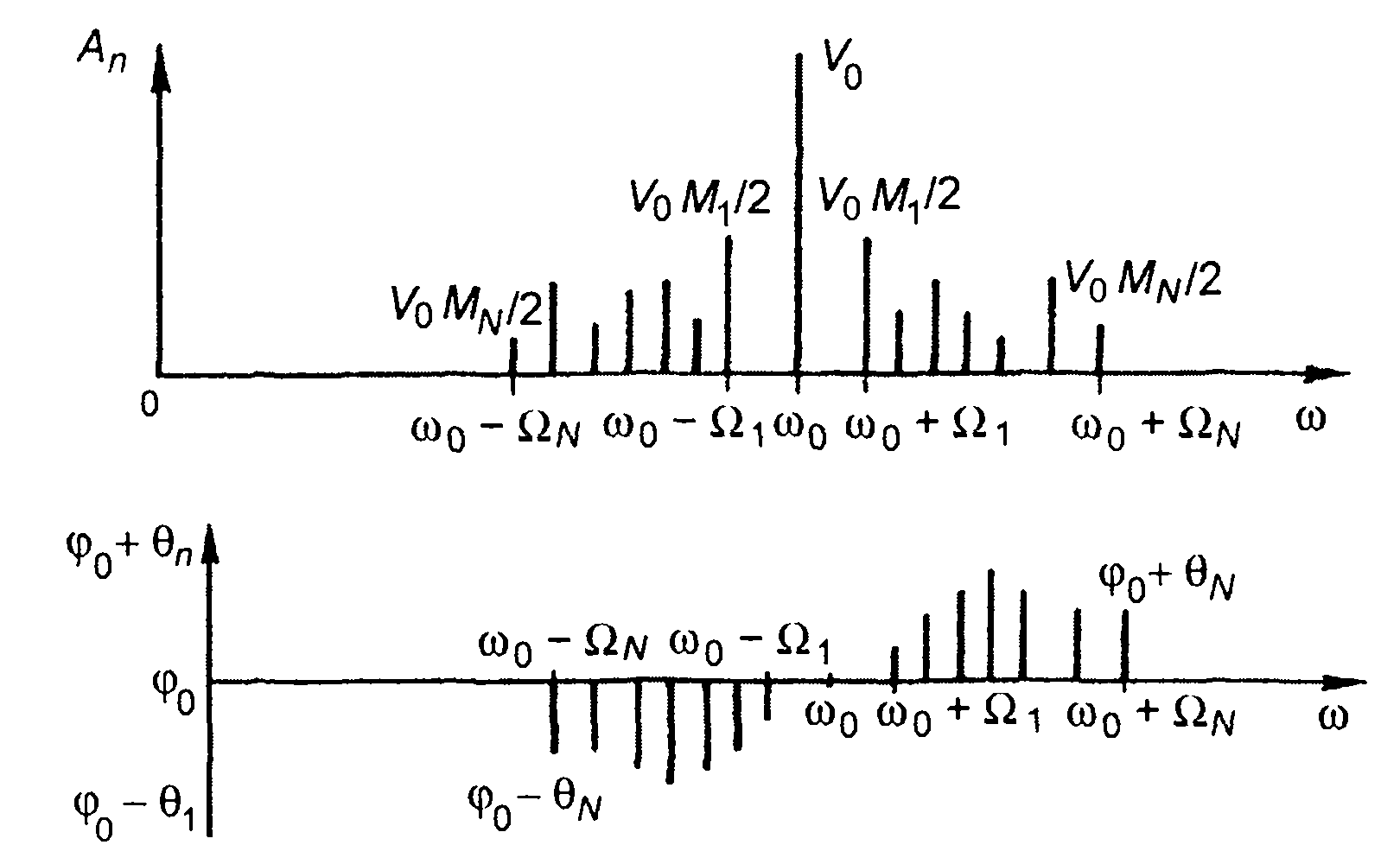
Рис. 9.4

На долю всех боковых составляющих приходится

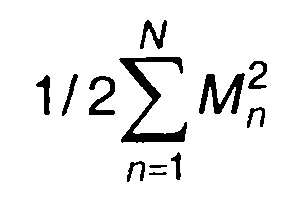
от мощности несущего колебания.

9.4. Амплитудная модуляция периодической последовательностью импульсов

Одним из видов многотональных AM сигналов является перио­дическая последовательность радиоимпульсов (рис. 9.5). Такой AM сигнал удобнее записать в виде