ДЕТЕРМИНИРОВАННЫЕ СИГНАЛЫ 9 страница

(9.12)

где s(t) - модулирующая периодическая последовательность ви­деоимпульсов.

Модулирующий сигнал s(t) описывается рядом Фурье (раздел 3)

(9.13)

где Ω = 2π/ Т, Т- период последовательности импульсов.

Рис. 9.5

Амплитуды s_n и начальные фазы Θn определяются следующи­ми выражениями:

(9.14)

где S(ω) - спектральная плотность одного импульса модулирующей последовательности.

Подставив (9.13) в (9.12), получим

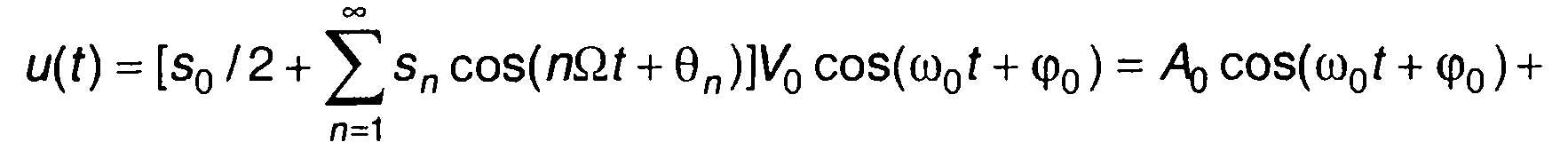
(9.15)

где A₀ = V₀s₀/2, А_n = V₀s_n/2, n = 1,2…

Как следует из (9.15), спектр сигнала является дискретным, рас­положен в окрестности несущей частоты ω₀. Огибающая дискрет­ного спектра периодической последовательности радиоимпульсов по форме совпадает с непрерывным спектром одиночного видео­импульса модулирующей последовательности.

Используя табл.3.1, из (9.14) можно найти спектры периодиче­ских последовательностей радиоимпульсов различной формы. Та­кой подход иллюстрируют следующие примеры.

1. Периодическая последовательность прямоугольных радиоимпульсов.

Модулирующий сигнал описывается выражением (табл. 3.1, п.1).

где т, Т = 2π/ω₁ - длительность и период следования периодиче­ской последовательности прямоугольных импульсов.

Подставляя выражение для s(t) в (9.12), при φ₀ = 0 получим

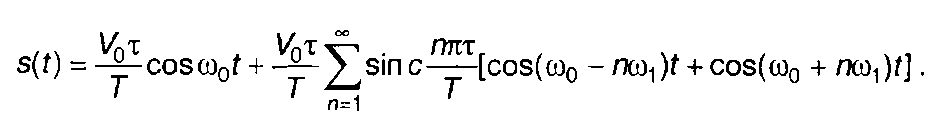
Амплитудный спектр описывается выражением

Рис. 9.6

На рис. 9.6 спектр изображен при ω > 0.

2. Периодическая последовательность симметричных тре­угольных радиоимпульсов.

Амплитудный спектр описывается выражением (табл. 3.1, п.З), рис. 9.7

3. Периодическая последовательность косинусоидальных ра­диоимпульсов.

Рис. 9.7

Амплитудный спектр описывается выражением (табл. 3.1,п.4), рис. 9.8

9.5. Амплитудная модуляция непериодической последовательностью импульсов

Одиночный радиоимпульс описывается выражением

(9.16)

где s(t) - модулирующий импульс; т - длительность модулирующе­го видеоимпульса.

В (9.16) s(t) представляет огибающую модулирующего импульса. Спектральная плотность сигнала (9.16) определяется преобразова­нием Фурье (разд. 3)

(9.17)

где S(ω) - спектральная плотность модулирующего сигнала s(t). При φ₀ =0 (рис. 9.9, а,б)

(9.18)

Примеры одиночных радиоимпульсов взяты для модулирующих сигналов, описанных в табл. 3.1, при φ₀ = 0.

Рис. 9.8

Рис. 9.9

1 .Прямоугольный радиоимпульс (табл. 3.1, п. 1), рис. 9.10 (ω> 0)

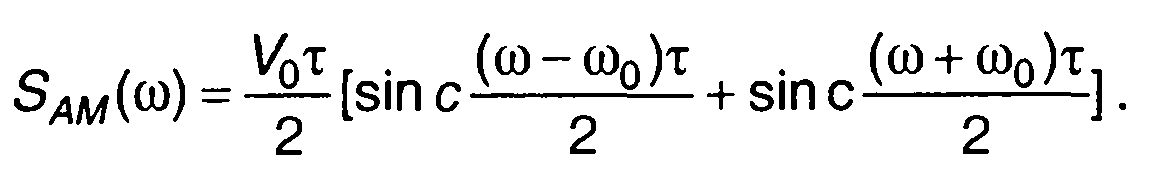
2. Гауссов радиоимпульс (табл. 3.1, п.15), рис. 9.11 (ω > 0)

Рис. 9.10

Рис. 9.11

Аналогично могут быть получены спектры пачек радиоимпуль­сов. Модулирующим сигналом является пачка видеоимпульсов. Спектральная плотность пачки радиоимпульсов может быть полу­чена из (9.17) с учетом выражений, приведенных в разд. 3.

(9.19)

где S₀(ω) - спектральная плотность одного видеоимпульса в пачке;

Т- интервал следования импульсов в пачке.

Амплитудный спектр в области положительных частот описыва­ется выражением

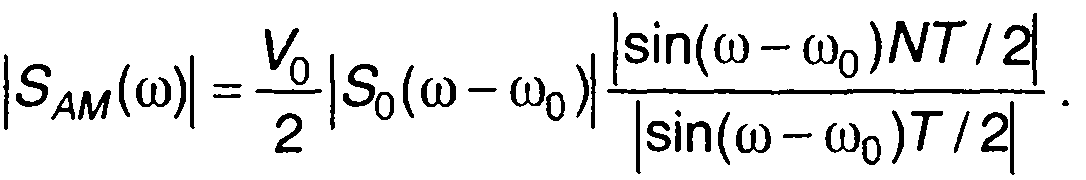(9.20)

Используя (9.21) и табл. 3.1, можно найти спектры пачек радио­импульсов различной формы. Такой подход иллюстрируется сле­дующими примерами.

1. Пачка прямоугольных радиоимпульсов (табл. 3.3, п.1), рис. 9.12.

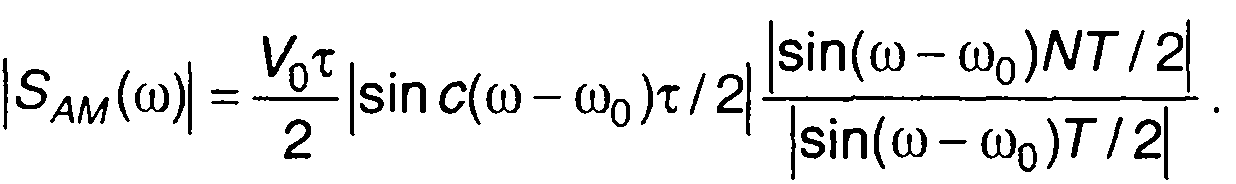
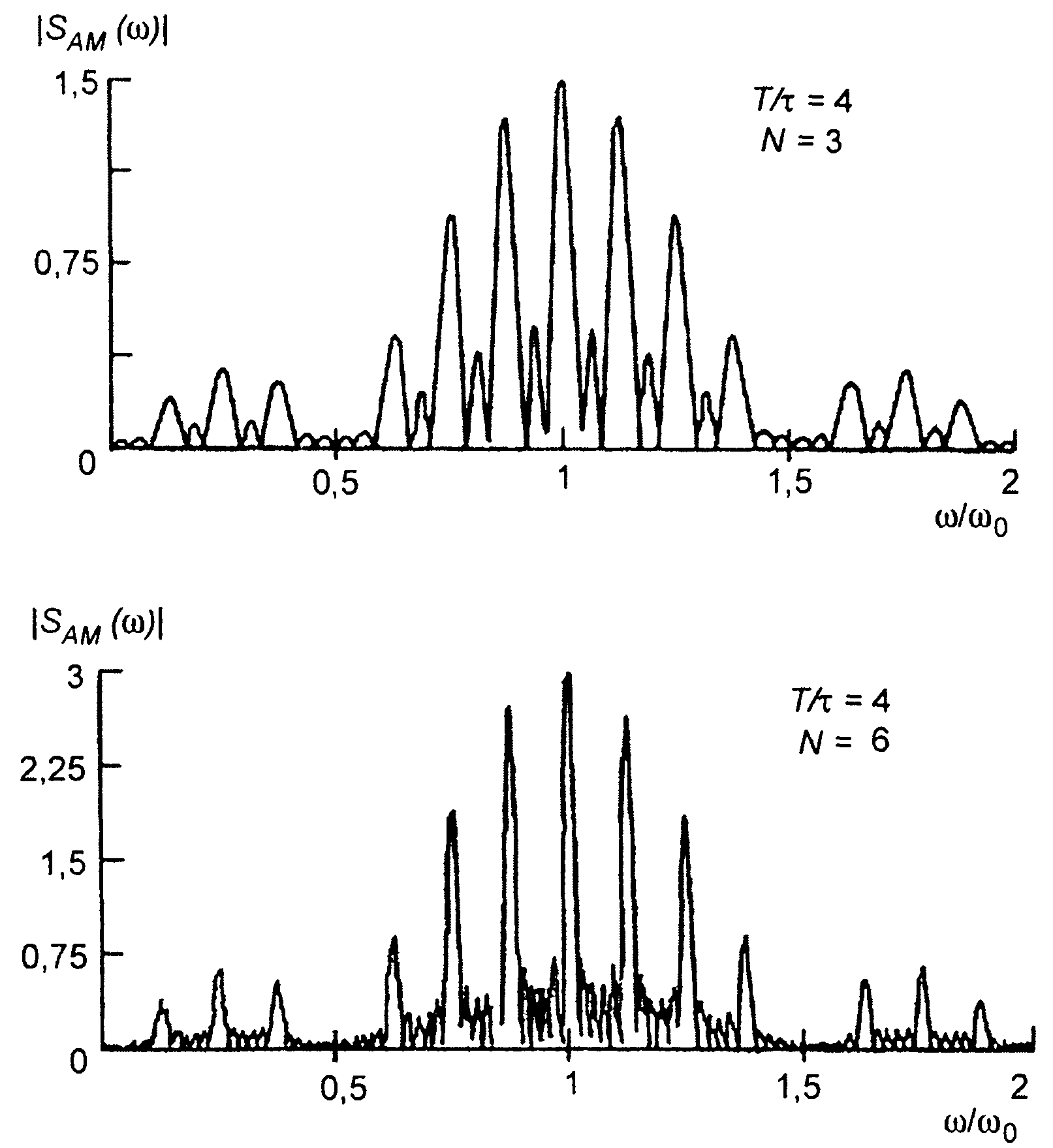
Рис. 9.12

2. Пачка треугольных радиоимпульсов (табл. 3.1, п.З), рис. 9.13

3. Пачка гауссовых радиоимпульсов (табл. 3.1, п. 15), рис. 9.14

Рис. 9.13

9.6. Балансная амплитудная модуляция

Балансная модуляция (БМ) является одним из видов амплитудной модуляции. Ее можно рассматривать как операцию, при которой производится перемножение модулирующего сигнала и несущего колебания. При балансной модуляции сигнал не содержит не­сущего колебания, это положительный момент при формировании AM сигнала.

Выражение для БМ сигнала записывается в виде

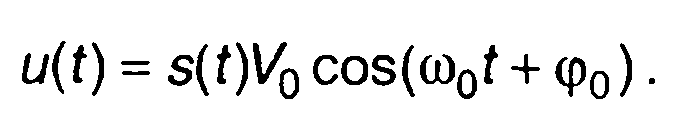(9.21)

Для тонально БМ сигнала

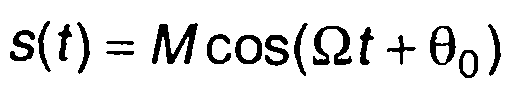(9.22)

имеем

Рис. 9.14

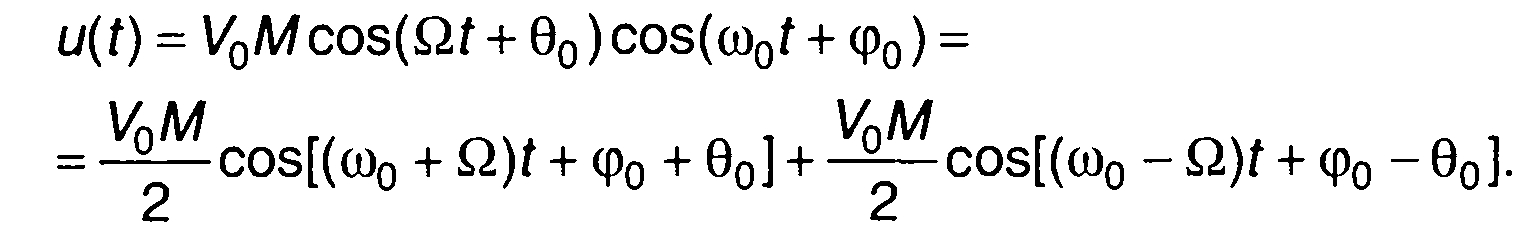(9.23)

Как следует из (9.23), при балансной модуляции спектр модули­рующего сигнала переносится в окрестность несущей частоты. Однако сама несущая отсутствует (подавляется). Вследствие этого такой вид модуляции называется амплитудной модуляцией без не­сущей.

Выражение для многотонального БМ сигнала получится из (9.21) с учетом (9.9)

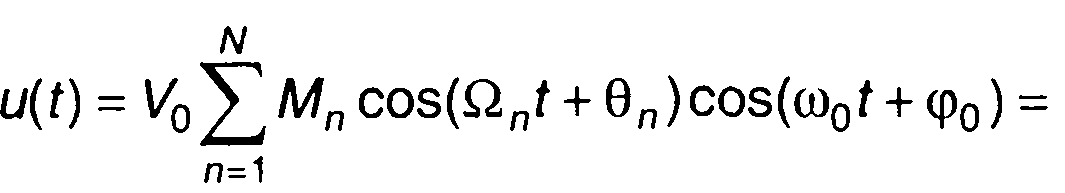(9.24)

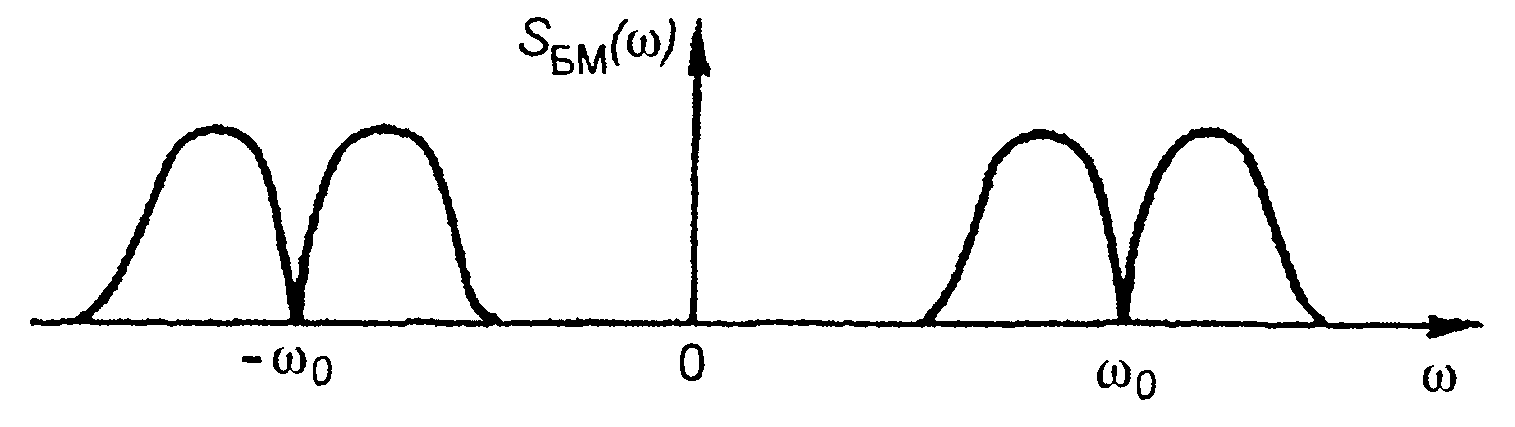
Рис. 9.15

Амплитудный спектр сигнала (9.24) показан на рис. 9.15.

Спектр включает две симметричные полосы верхних и нижних бо­ковых составляющих. Ширина спектра БМ сигнала определяется вы­ражением (9.11). Средняя мощность многотонального БМ сигнала

(9.25)

значительно меньше, чем при обычной амплитудной модуляции (9.12).

Спектральная плотность БМ сигнала может быть определена исходя из (9.21). При φ₀ = 0 получим (рис. 9.16),

(9.26)

Как указано, при балансной модуляции уменьшается мощность передатчика по сравнению с обычной амплитудной модуляцией. В то же время необходимая полоса частот остается такой же. В обоих случаях получаются две боковые полосы, каждая из которых несет информацию, содержащуюся в модулирующем сигнале. Сузить не­обходимую полосу частот можно, если подавить в спектре AM сигна­ла несущую и одну боковую полосу.

Рис. 9.16

Рис. 9.17

Такой вид амплитудной модуляции называется однополосной ам­плитудной модуляцией с подавленной несущей или просто однопо­лосной амплитудной модуляцией.

9.7. Однополосная амплитудная модуляция

При однополосной амплитудной модуляции (ОМ) сигнал содер­жит только одну боковую полосу частот. Выражение для многото­нального ОМ сигнала получаем из (9.9)

(9.27)

Знак плюс в (9.27) соответствует сигналу с верхней боковой по­лосой частот (рис. 9.17), а знак минус - с нижней боковой полосой. При однополосной амплитудной модуляции ширина спектра

(9.28)

где Ω_n - максимальная частота модуляции, что вдвое уже, чем при

обычной амплитудной модуляции, описываемой (9.10).

Средняя мощность многотонального ОМ сигнала равна

Рис. 9.18

(9.29)

Спектральная плотность ОАМ-сигнала описывается выражением

(9.30)

Знак плюс в (9.30) соответствует описанию спектра с подавленной нижней боковой полосой, а минус - с подавленной верхней полосой (рис. 9.18).

Раздел 10.

СИГНАЛЫ С ФАЗОВОЙ И ЧАСТОТНОЙ МОДУЛЯЦИЕЙ

Сигналы с угловой модуляцией, как правило, являются узкопо­лосными. Ширина их спектра значительно меньше несущей часто­ты. Такие сигналы и рассматриваются в разделе.

10.1. Описание сигналов с угловой модуляцией

Узкополосный сигнал с угловой модуляцией описывается выра­жением (рис. 10.1,а)

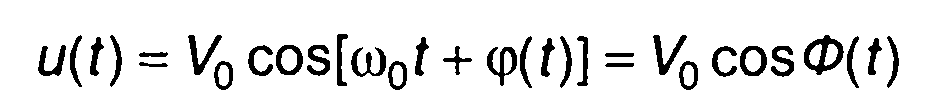(10.1)

или в комплексной форме

(10.2)

где V(t) = V₀e^iφ(t) - комплексная огибающая сигнала; V₀,ω₀,φ(t)-

амплитуда, частота и фаза сигнала.

Комплексный сигнал может быть представлен в виде вектора дли­ны V₀на комплексной плоскости (рис. 10.1,6). Вектор составляет с дей­ствительной осью угол φ(t), который изменяется во времени. Сама система координат вращается по часовой стрелке с угловой скоростью ω₀. Проекция вектора на действительную ось описывает сигнал u(t).

Понятие угловой модуляции включает фазовую и частотную мо­дуляцию. При фазовой модуляции (ФМ) под воздействием модули­рующего сигнала s(t) изменяется непосредственно фаза φ(f).

Обычно обеспечивается линейная зависимость фазы от модули­рующего сигнала:

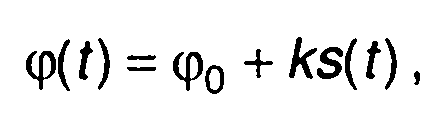(10.3)

где φ₀ - начальная фаза; k - коэффициент пропорциональности. Мгновенная частота ФМ сигнала

(10.4)

Рис.10.1

При частотной модуляции (ЧМ) модулирующий сигнал воздейст­вует непосредственно на частоту

(10.5)

Фаза ЧМ сигнала

(10.6)

Максимальное отклонение фазы от начальной φ₀

называется индексом модуляции. Максимальное отклонение часто­ты ω(t) от несущей ω₀

- девиацией частоты, или девиацией.

Отличие ФМ от ЧМ легче просматривается при простейшем - тональном (гармоническом) законе модуляции:

(10.7)

где s₀ , Ω - амплитуда и частота модулирующего сигнала.

При тональной ФМ (рис. 10.2)

(10.8)

сигнал описывается выражением

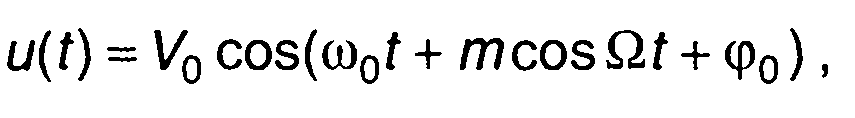(10.9)

частота равна

(10.10)

Девиация определяется произведением индекса модуляции и частоты модуляции

(10.11)

При тональной ЧМ частота (рис. 10.3)

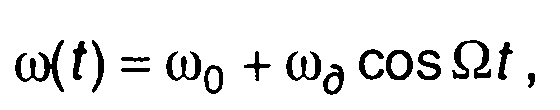(10.12)

фаза

(10.13)

Сигнал описывается выражением

(10.14)

Индекс модуляции определяется отношением девиации к часто­те модуляции. Таким образом, тонально модулированный ФМ сиг­нал с индексом модуляции т описывается аналогичным выражени­ем, что и ЧМ сигнал с девиацией, равной mΩ. Отличие заключается в том, что фаза ФМ сигнала изменяется по закону т cosΩt, а фаза ЧМ сигнала - по закону ω_g/ΩsinΩt.

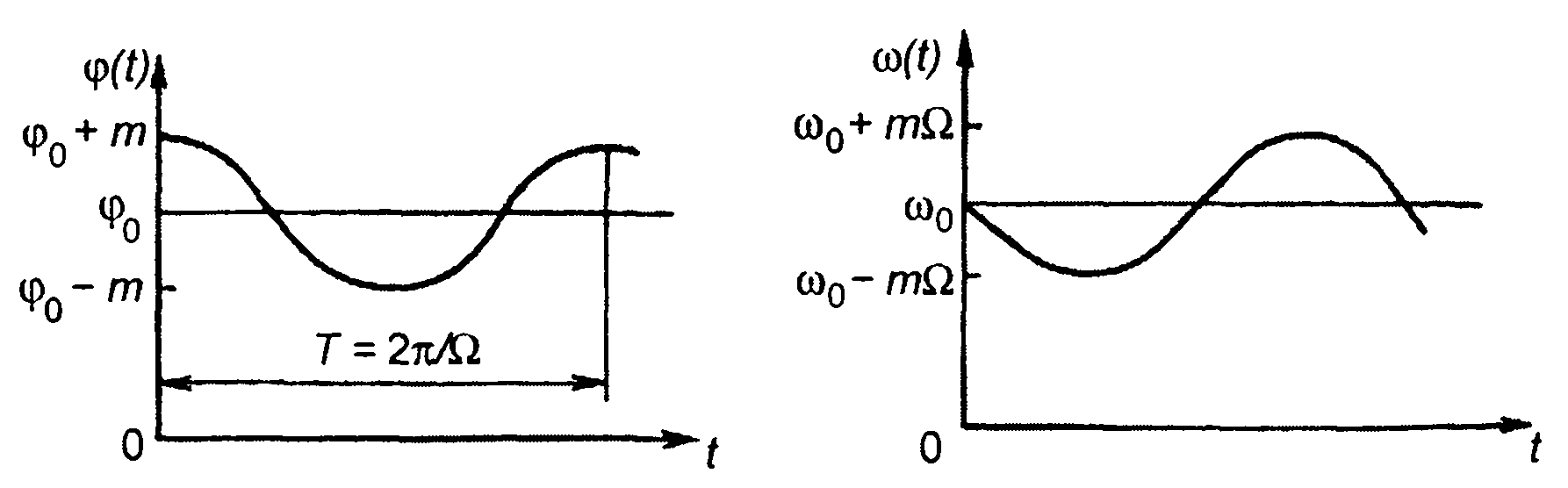
Рис. 10.2

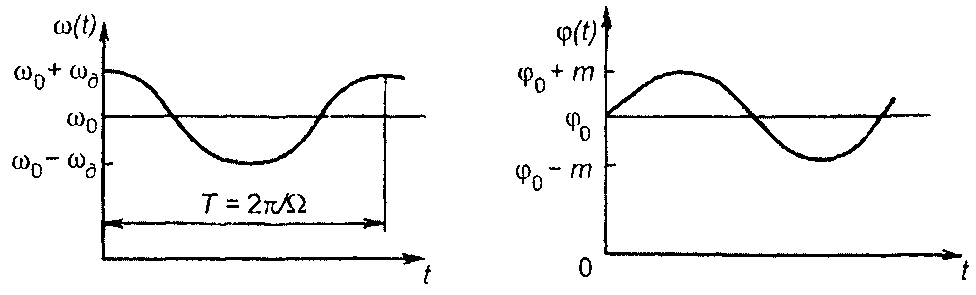
Рис. 10.3

При ЧМ девиация пропорциональна амплитуде модулирующего сигнала и не зависит от его частоты. При ФМ индекс модуляции пропорционален амплитуде модулирующего сигнала и не зависит от частоты этого сигнала.

10.2. Сигнал с тональной угловой модуляцией

Простейший вид модуляции - тональный. Сигнал с тональной угловой модуляцией запишем в виде

(10.15)

где

Спектр сигнала определяется при разложении в ряд Фурье ком­плексной огибающей сигнала. При φ0 = 0

Используя соотношение, известное из теории Бесселевых функций

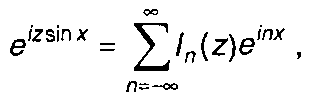(10.16)

где ln(z) - функция Бесселя первого рода n-го порядка от аргумента z,

для комплексной огибающей сигнала получим

(10.17)

Подставляя (10.17) в (10.15), запишем

(10.18)

Анализ (10.18) показывает следующее. Спектр сигнала с угловой тональной модуляцией является дискретным. Гармоники спектра отличаются друг от друга на частоты, кратные частоте модуляции.

Амплитуды составляющих спектра определяются функциями Бесселя. Функции Бесселя являются специальными функциями, описываются выражением

(10.19)

Графики функций Бесселя изображены на рис. 10.4.

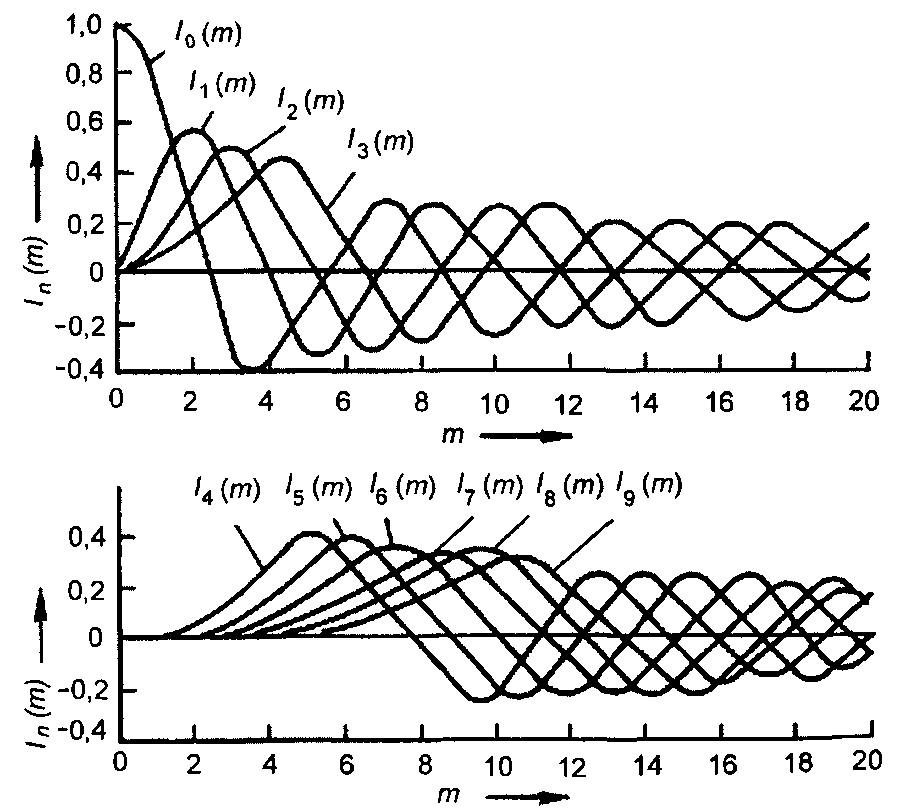
Рис. 10.4

Как следует из (10.18), сигнал с угловой тональной модуляцией включает несущее колебание с амплитудой V₀l₀(m) и бесконечное множество парных боковых составляющих с частотами ω₀ ± nΩ. и амплитудами V₀l_n(m). Причем фазы верхних и нижних составляю­щих сигнала нечетных номеров п отличаются на величину π. Ам­плитудные спектры сигналов для некоторых значений т приведены на рис. 10.5. Наибольшее значение амплитуды имеет составляю­щая, номер которой определяется эмпирическим выражением [20]

(10.20)

По мере увеличения номера n амплитуды боковых составляю­щих убывают, стремясь к нулю. Ширина спектра определяется эм­пирическим выражением

(10.21)

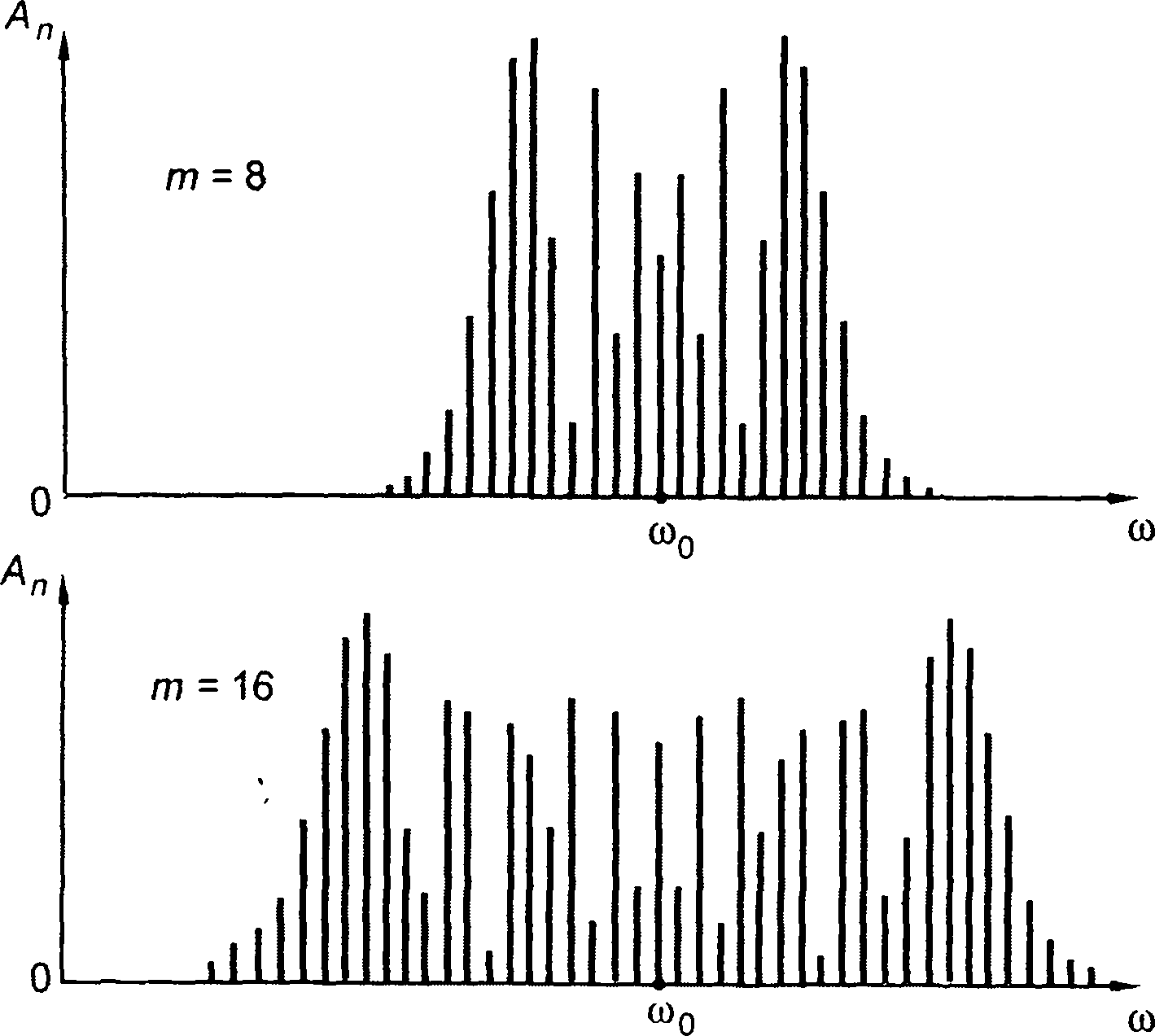
Рис.10.5

Как следует из (10.21), при увеличении индекса модуляции ши­рина спектра стремится к величине 2тΩ (или 2ω_д). Следовательно, при больших индексах модуляции ширина спектра сигнала, можно считать, равна удвоенному значению девиации. При малом индексе модуляции ширина спектра стремится к удвоенному значению час­тоты модуляции (2Ω).

При малом индексе модуляции (т<<1) можно принять

(10.22)

С учетом (10.22) выражение (10.18) запишется в виде

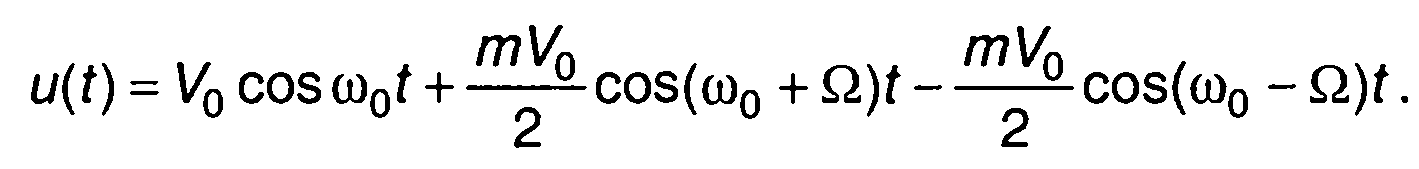(10.23)

Спектр такого сигнала подобен спектру AM сигнала и включает: несущее колебание с амплитудой V₀ и две боковые составляющие с частотами ω₀ ± Ω и амплитудами mV_o/2. Причем фаза нижней со­ставляющей смещена по отношению к верхней на величину π. Ши­рина спектра равна удвоенной частоте модуляции (2Ω).

Средняя мощность сигнала с угловой модуляцией может быть определена из (10.18) как

(10.24)

где Р₀ = V₀² / 2 средняя мощность несущего колебания;

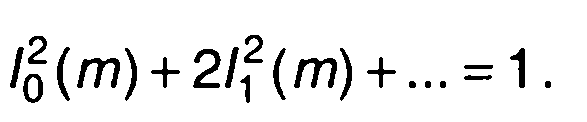(10.25)

Как следует из (10.24), средняя мощность сигнала с угловой мо­дуляцией равна средней мощности несущего колебания.

10.3. Сигнал со сложным периодическим законом модуляции

Любой периодический модулирующий сигнал можно разложить в ряд Фурье, представить в виде взвешенной суммы гармонических составляющих. Условия, необходимые для такого разложения, обыч­но выполняются. Однако использование разложения при определе­нии спектра сигнала с угловой модуляцией (путем подстановки в (10.1) или (10.2) разложения φ(t) в ряд Фурье) приводит к выражению, неприемлемому для целей анализа и расчета спектра сигнала.

Исключение составляют законы угловой модуляции, которые приводят только к изменению огибающей сигнала. К таким модулирующим сиг­налам относится меандр. В других случаях более удобным оказыва­ется подход, при котором определяется спектр импульсного ЧМ сиг­нала с длительностью, равной периоду непрерывного сигнала, а за­тем выполняется переход к спектру периодического сигнала. Ниже дано определение спектра сигналов с некоторыми достаточно рас­пространенными законами угловой модуляции.

10.3.1. ФМ сигнал с модуляцией меандром

При модуляции гармонического колебания меандром происходит скачкообразное изменение модулируемого параметра - манипуля­ция; при ФМ -скачкообразное изменение фазы (рис. 10.6,а)

(10.26)

где Т - период модуляции.

Комплексная огибающая такого сигнала определяется как (рис.10.6,б)

(10.27)

Спектр сигнала удобнее определить через спектр огибающей. Раскладывая в ряд Фурье огибающую сигнала, запишем (разд. 3)

(10.28)

где Ω = 2π/T- частота модуляции.

Рис. 10.6

С учетом (10.28) из (10.2) получим следующее выражение для ФМ сигнала:

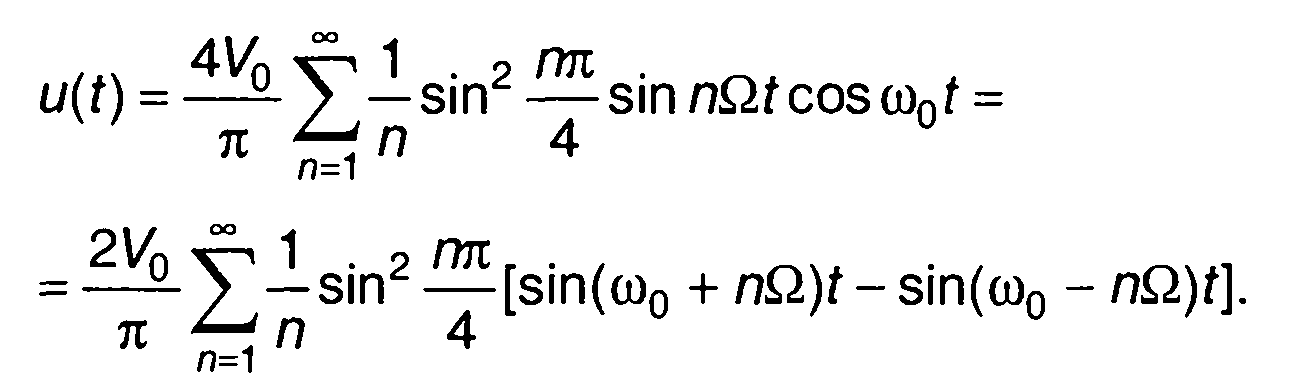(10.29)

Спектр сигнала (10.29) изображен на рис. 10.7.

Аналогичный подход позволяет получить спектр ФМ сигнала, ог­раниченного N периодами огибающей (ФМ пачкой прямоугольных импульсов), рис. 10.8. Спектральная плотность такого сигнала дли­тельности NT, где N - число импульсов в пачке, Г - период следо­вания импульсов в пачке, определяется выражением

(10.30)

где U(ω) - спектральная плотность огибающей сигнала.

Огибающая сигнала V(t) представляет отрезок меандра (рис. 10.8,б).

Спектр пачки меандровых импульсов описывается выражением (разд. 3)

(10.31)

где τ_и - длительность импульса; Г - период следования импульсов в пачке.

Так как Т = 2τ_и, (10.31) можем переписать в виде

Рис. 10.7

Рис. 10.8

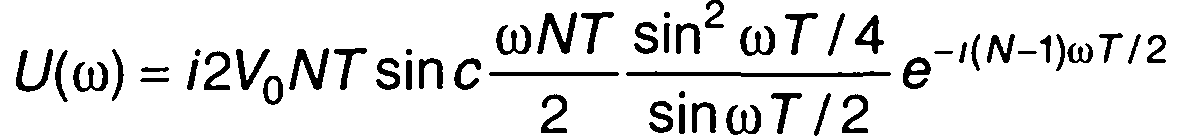(10.32)

Таким образом, выражение для спектра ФМ сигнала, модулиро­ванного пачкой меандровых импульсов, примет вид

(10.33)

Первое слагаемое в (10.33) описывает спектральную плотность сигнала в области положительных частот, второе в области отри­цательных частот. Амплитудный спектр сигнала в области положи­тельных частот определяется как

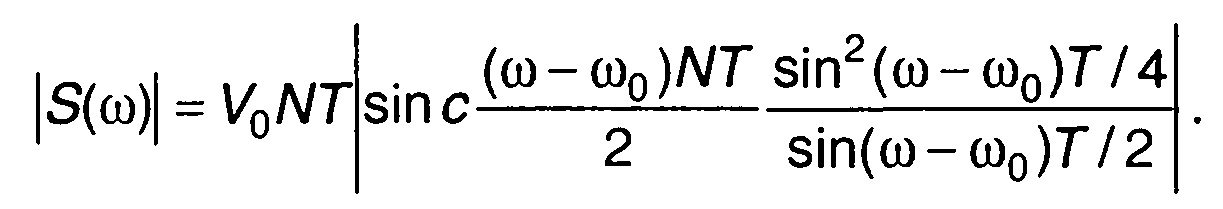(10.34)

Он симметричен относительно несущей частоты ω₀,|S(ω₀)| = 0 (рис. 10.9).

Рис. 10.9

10.3.2. ЧМ сигнал с модуляцией меандром

При ЧМ меандром изменяется скачкообразно мгновенное значе­ние частоты (рис. 10.10)

где Т- период модуляции.

Частотно-модулированный сигнал представим в виде суммы двух сигналов

(10.35)

где u₁(t), u₂(t) - периодические последовательности прямоуголь­ных радиоимпульсов с несущими частотами ω₁ и ω₂ , периодом Т и длительностью Т/2, смещенные относительно начала координат на ± Т/4.

Рис. 10.10

Спектры ui(t) и u₂(t) определяются выражениями (разд. 3)

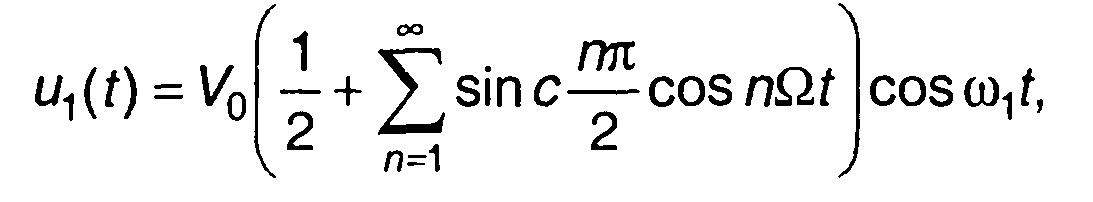
(10.36)

Из (10.35) с учетом (10.36) получим выражение для периодиче­ского ЧМ сигнала

Графики амплитудного спектра сигнала при различных соотно­шениях ω₁ и ω₂ приведены на рис. 10.11. Частоты ω₁ и ω₂ , как пра­вило, выбираются кратными частоте модуляции Ω = 2π/Т, что и от­ражено на графиках. Как следует из (10.37), спектр сигнала включа­ет два несущих колебания с частотами ω₁ и ω₂ и бесконечное число боковых составляющих с частотами ω₁ ±nΩ и ω₂ ±nΩ.

Рис. 10.11

Аналогичный подход используем при определении спектра ЧМ сигнала, модулированного пачкой прямоугольных импульсов (рис. 10.12).

При ЧМ пачкой прямоугольных импульсов сигнал можно пред­ставить в виде (10.35), где u₁(t) и u₂(t) обозначают пачки из N пря­моугольных радиоимпульсов с несущими частотами ω₁ и ω₂ . Спек­тральная плотность такого сигнала описывается выражением (свойства преобразования Фурье)

(10.38)

где S₁(ω) , S₂(ω) - спектральные плотности сигналов u₁(t) и u₂(t). Спектральные плотностиS₁(ω) , S₂(ω)определяются как

(10.39)

(10.40)

где U(ω) - спектральная плотность пачки из N прямоугольных ви­деоимпульсов (разд. 3).

С учетом (10.38) - (10.40) выражение для спектра сигнала запи­шем в виде

(10.41)

Выражение для U(ω) имеет вид

(10.42)

или

(10.43)

Подстановка (10.43) в (10.41) для ω > 0 дает

(10.44)

Г рафики амплитудного спектра |S(ω)|, построенные при различ­ных соотношениях частот ω₁ и ω₂ приведены на рис. 10.13. Ампли­тудный спектр имеет максимумы на несущих частотах ω₁ и ω₂ .

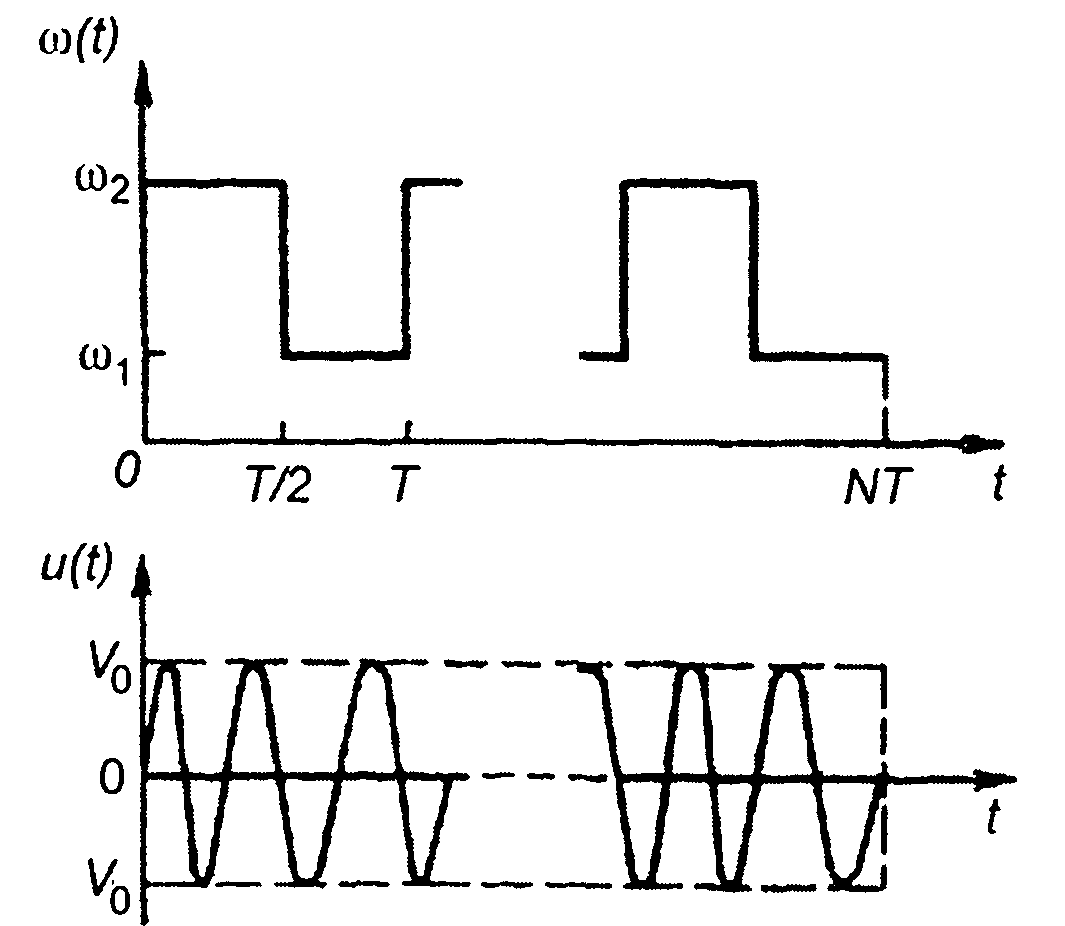
Рис. 10.12

Рис. 10.13

10.3.3. ЧМ сигнал с пилообразным несимметричным законом модуляции

Чтобы определить спектр непрерывного периодического ЧМ сигнала с пилообразным несимметричным законом модуляции (рис. 10.14,а), рассмотрим импульсный сигнал с внутриимпульсной ЧМ по линейному несимметричному закону (рис. 10.14,6). Длитель­ность импульсного сигнала равна периоду следования непрерывно­го сигнала. Частота такого сигнала описывается выражением