ДЕТЕРМИНИРОВАННЫЕ СИГНАЛЫ 12 страница

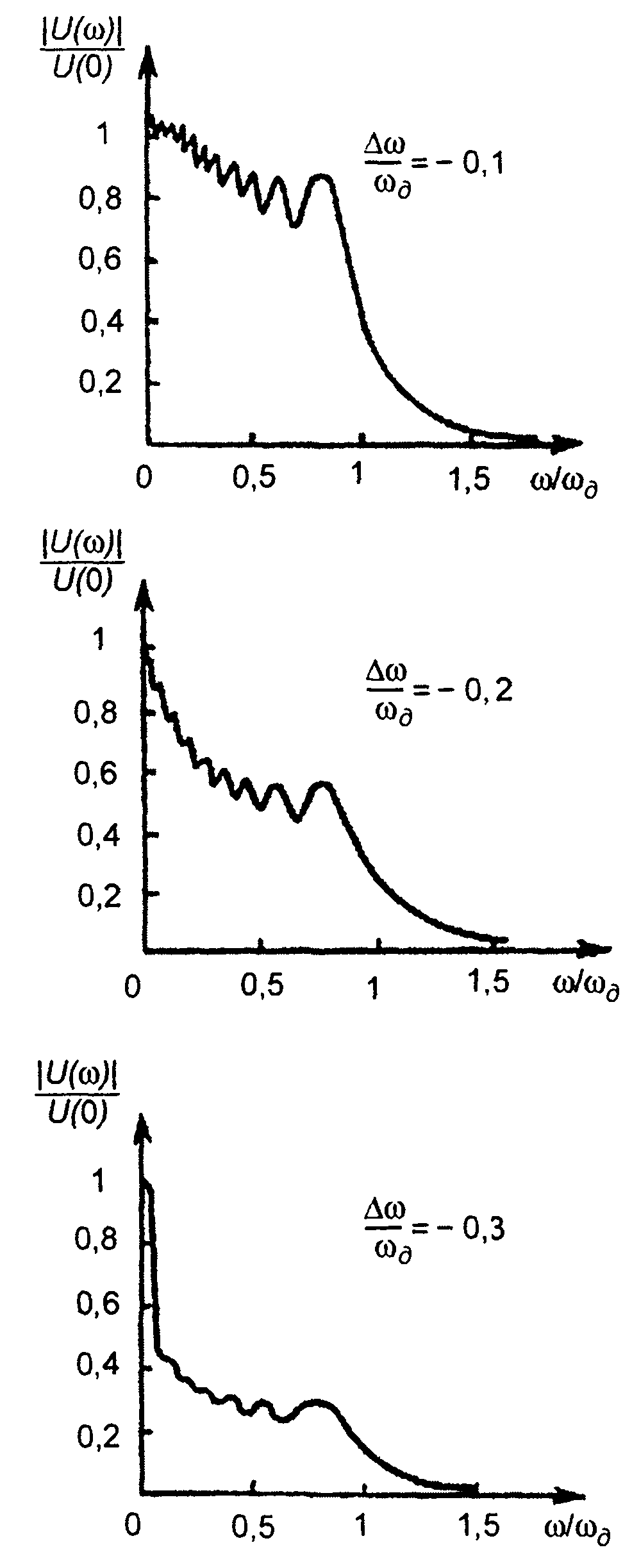
Рис. 11.20

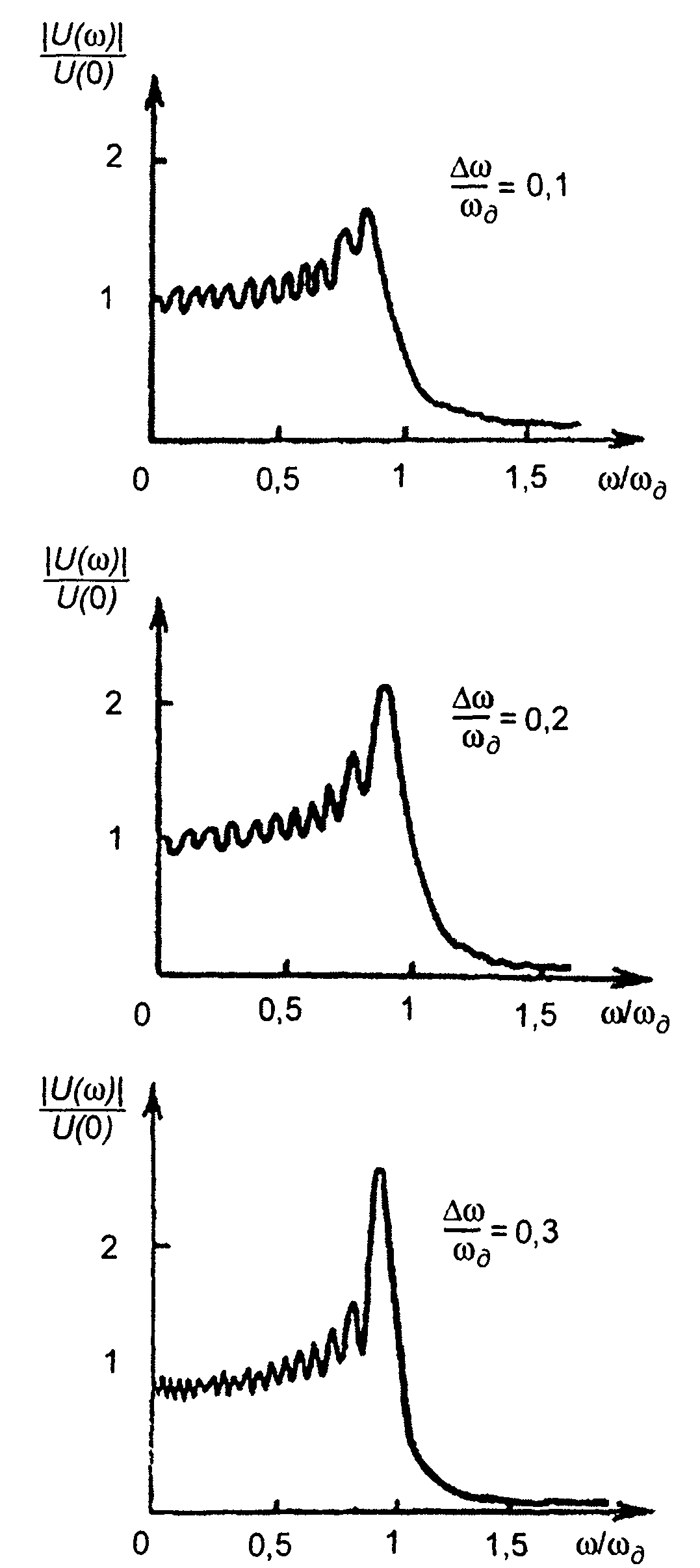
Рис. 11.21

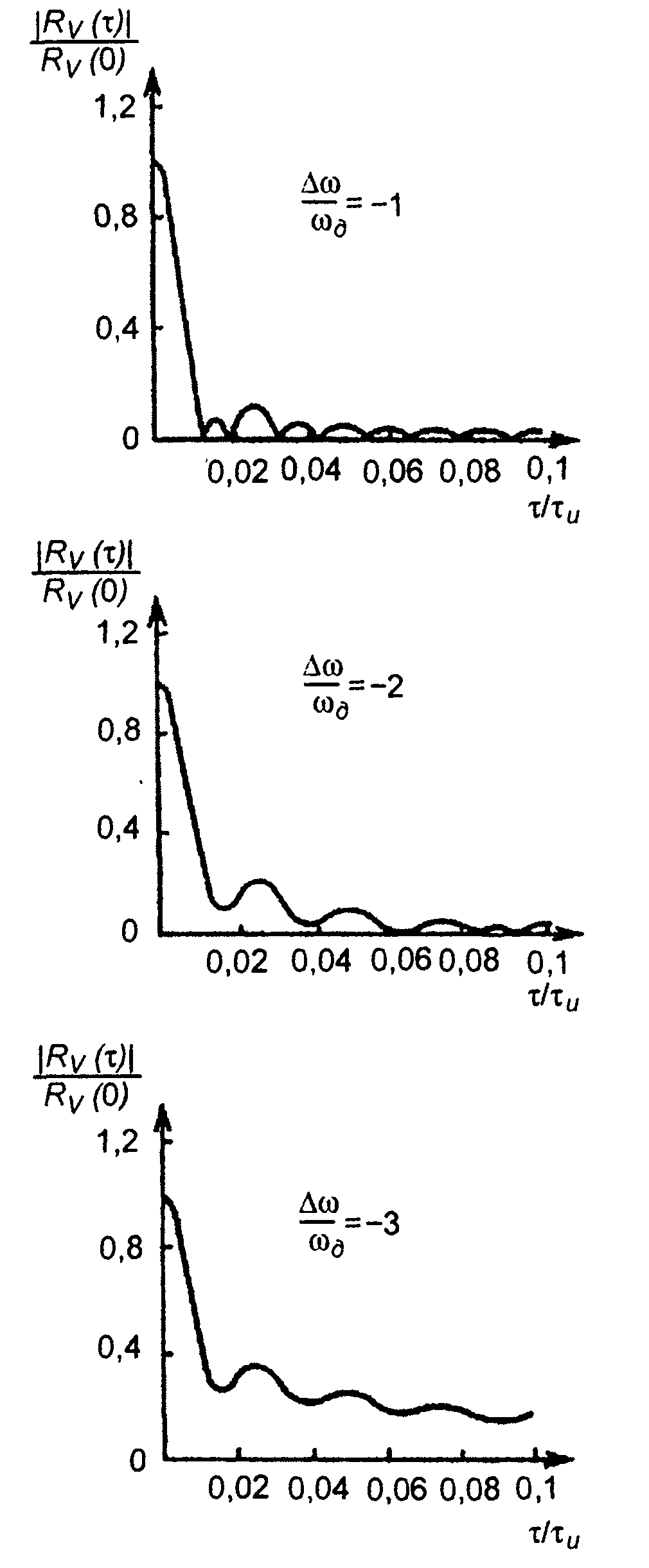
Рис. 11.22

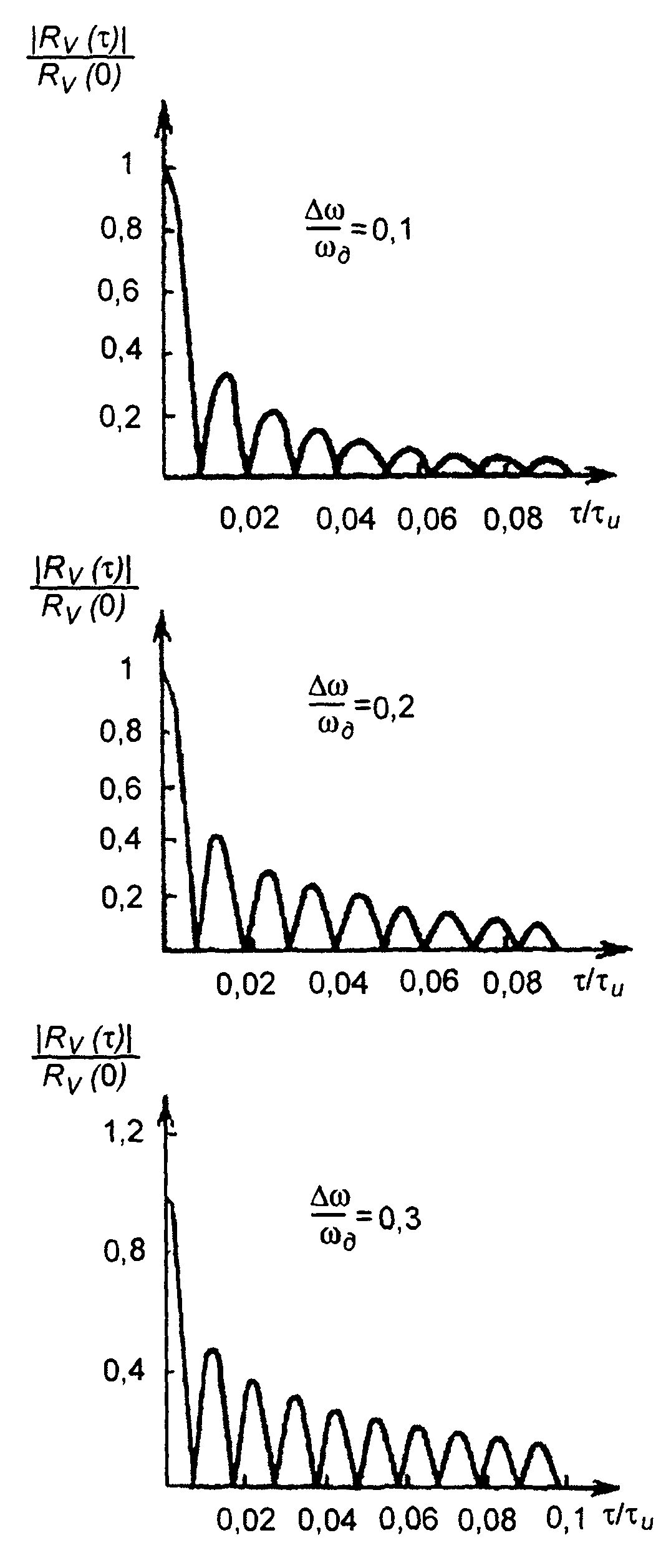
Рис. 11.23

Раздел 12.

КОДИРОВАННЫЕ СИГНАЛЫ

Особую группу модулированных сигналов составляют коди­рованные сигналы, которые получаются путем модулирования гармонического колебания упорядоченной последовательностью импульсов. Такие последовательности называются кодовыми. Наибольшее применение нашли двоичные кодовые последова­тельности, которые описываются символами 0 и 1 или -1 и 1 (рис. 12.1). В зависимости от параметра несущего гармонического колебания, на который воздействует кодовый сигнал, различают амплитудно-кодированные, фазо-кодированные и частотно- кодированные сигналы.

Кодовые последовательности используются в различных радио­технических системах. Некоторые виды кодовых последовательно­стей - при формировании радиолокационных сигналов с требуе­мыми корреляционными свойствами. Такие сигналы называют шу­моподобными.

В разделе дается описание и анализ основных характеристик кодированных сигналов.

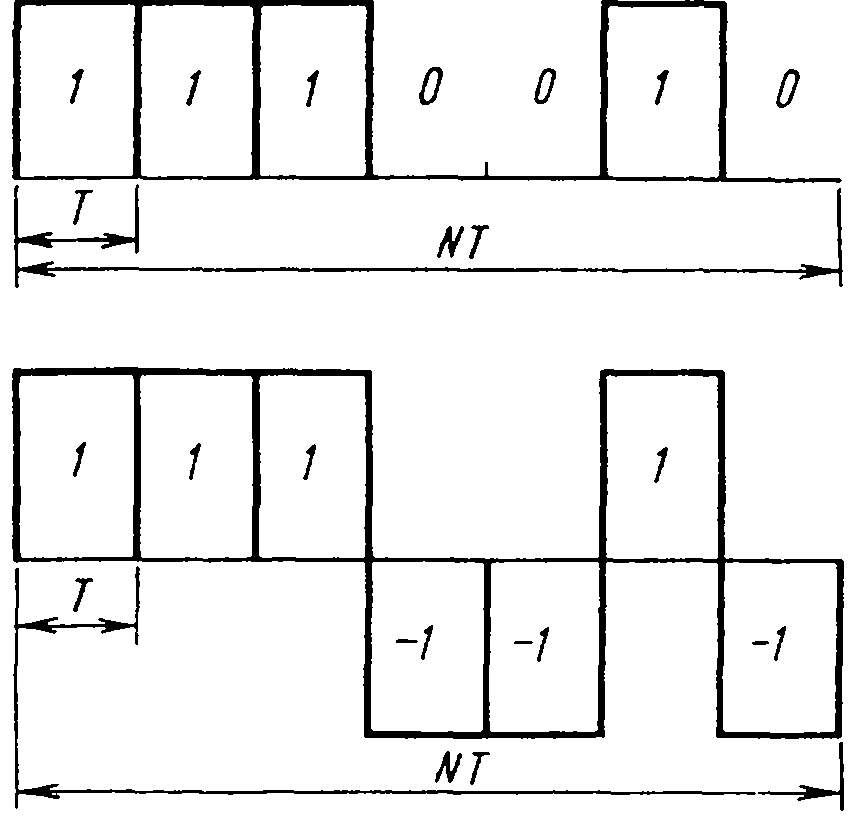
Рис. 12.1

12.1. Описание кодированных сигналов

Кодированные сигналы имеют вид последовательности (пачки) радиоимпульсов одинаковой формы и длительности, отличающих­ся друг от друга значениями амплитуд, начальных фаз или частот гармонического несущего колебания.

Одиночный радиоимпульс последовательности описывается выражением

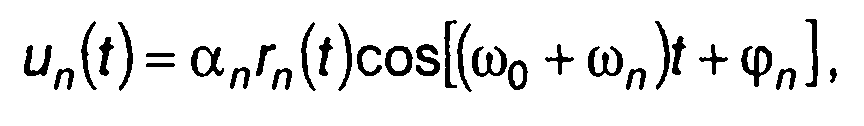(12.1)

где a_n, ω₀ + ω_n, φ_n - амплитуда, частота и начальная фаза гармо­нического колебания длительности Т на интервале времени (n-1)Т ≤ t ≤ nТ; ω₀ - центральная частота последовательности радиоим­пульсов; r_n(t) - функция, описывающая форму импульса.

Обычно используются прямоугольные импульсы, для которых

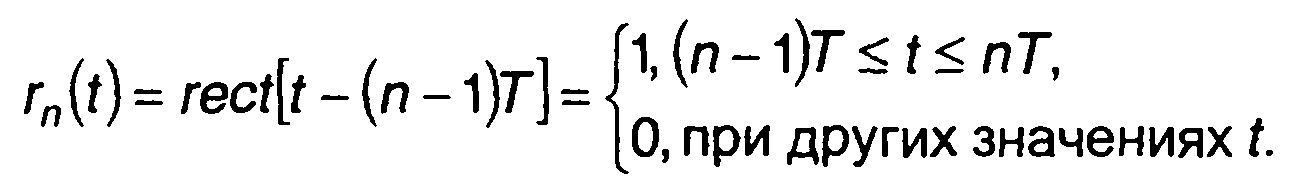(12.2)

Кодированный сигнал описывается выражением

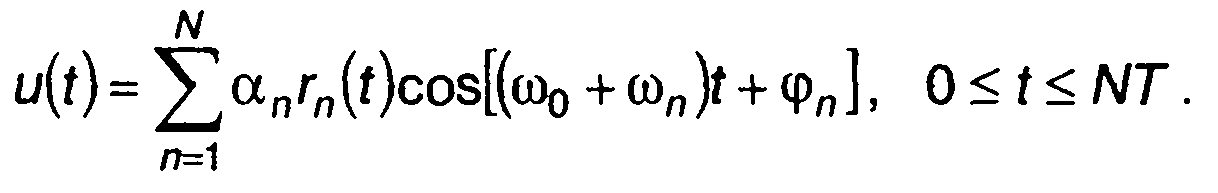(12.3)

Последовательности символов амплитуд {а_n}, фаз {φ_n} и частот {φ_n} составляют кодовые последовательности; N - число символов (длина) кодовой последовательности. Кодовые последо­вательности определяют закон изменения амплитуды, фазы и час­тоты гармонического несущего колебания.

В зависимости от вида модуляции различают: амплитудно-кодированные сигналы (изменяется a_n; (φ_n = 0, ω_n = 0); фазо-кодированные сигналы (изменяется (φ_n; а_n = 1, ω_n = 0); частотно-кодированные сигналы (изменяется ω_n; а_п = 1, φ_n = 0);

сигналы со смешанными видами модуляции (изменяются одновре­менно несколько параметров).

Кодированный сигнал, как правило, узкополосный. Выражение для него может быть записано в комплексной форме

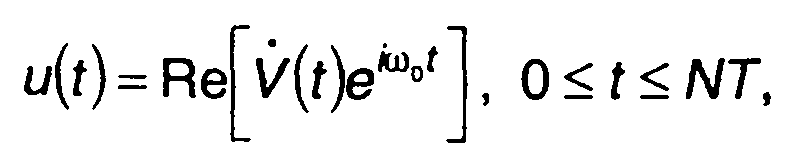(12.4)

Кодированные сигналы

где

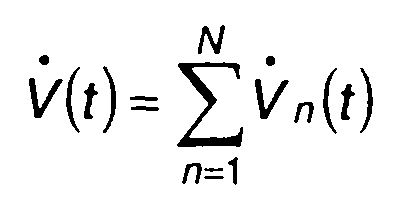(13.5)

- комплексная огибающая кодированного сигнала;

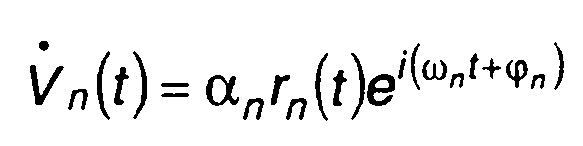(12.6).

- комплексная огибающая одиночного радиоимпульса (12.1).

Таким образом, кодированный сигнал описывается как последо­вательность радиоимпульсов, которые отличаются друг от друга лишь комплексными амплитудами.

Основными характеристиками кодированных сигналов являются спектр и корреляционная функция. Их удобнее определять через соответствующие характеристики комплексной огибающей сигнала. Для комплексной огибающей (12.5) эти характеристики описывают­ся следующими выражениями: спектральная плотность

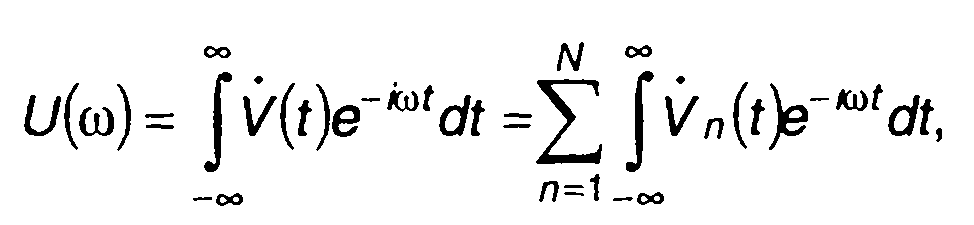(12.7)

корреляционная функция

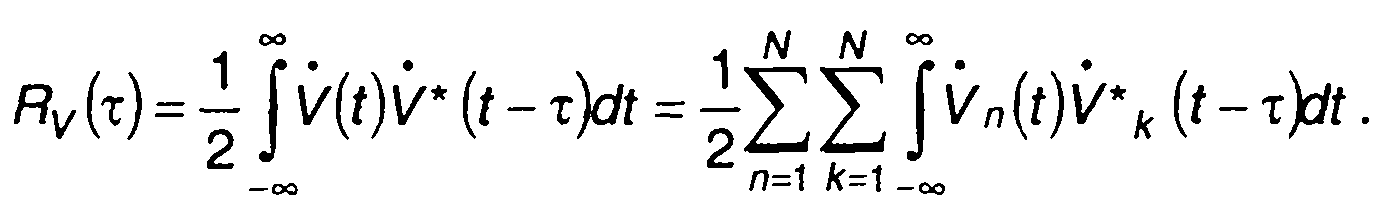(12.8)

С учетом очевидности перехода от U(ω) и R_v(τ) к спектральной плотности и корреляционной функции кодированного сигнала, ана­лиз кодированных сигналов в дальнейшем ограничен рассмотре­нием характеристик только комплексной огибающей. Указанные характеристики определены применительно к различным видам модуляции несущего колебания кодовой последовательностью.

12.2. Амплитудно-кодированные сигналы

Амплитудно-кодированный (АК) сигнал получается в результате амплитудной модуляции несущего гармонического колебания ко­довой последовательностью.

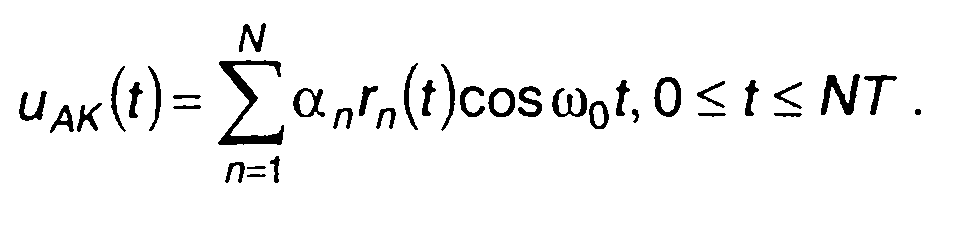(12.9)

Кодовая последовательность {а_n} определяет закон скачкооб­разного изменения амплитуды сигнала. При двоичном коде а_n принимает только два значения: 0 и 1. Таким образом, АК сигнал (12.9) представляет последовательность радиоимпульсов, которые отличаются лишь значениями амплитуд.

Комплексная огибающая сигнала

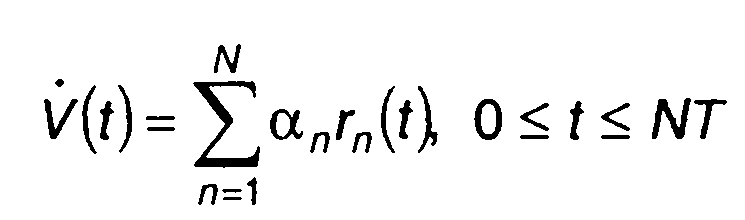(12.10)

совпадает с его огибающей и представляет последовательность видеоимпульсов r_n(t) с амплитудами а_n (0 или 1).

На рис. 12.2 и 12.3 приведены примеры АК сигналов.

12.2.1. Спектр комплексной огибающей АК сигнала

Спектральная плотность комплексной огибающей АК сигнала определится путем подстановки (12.10) в (12.7)

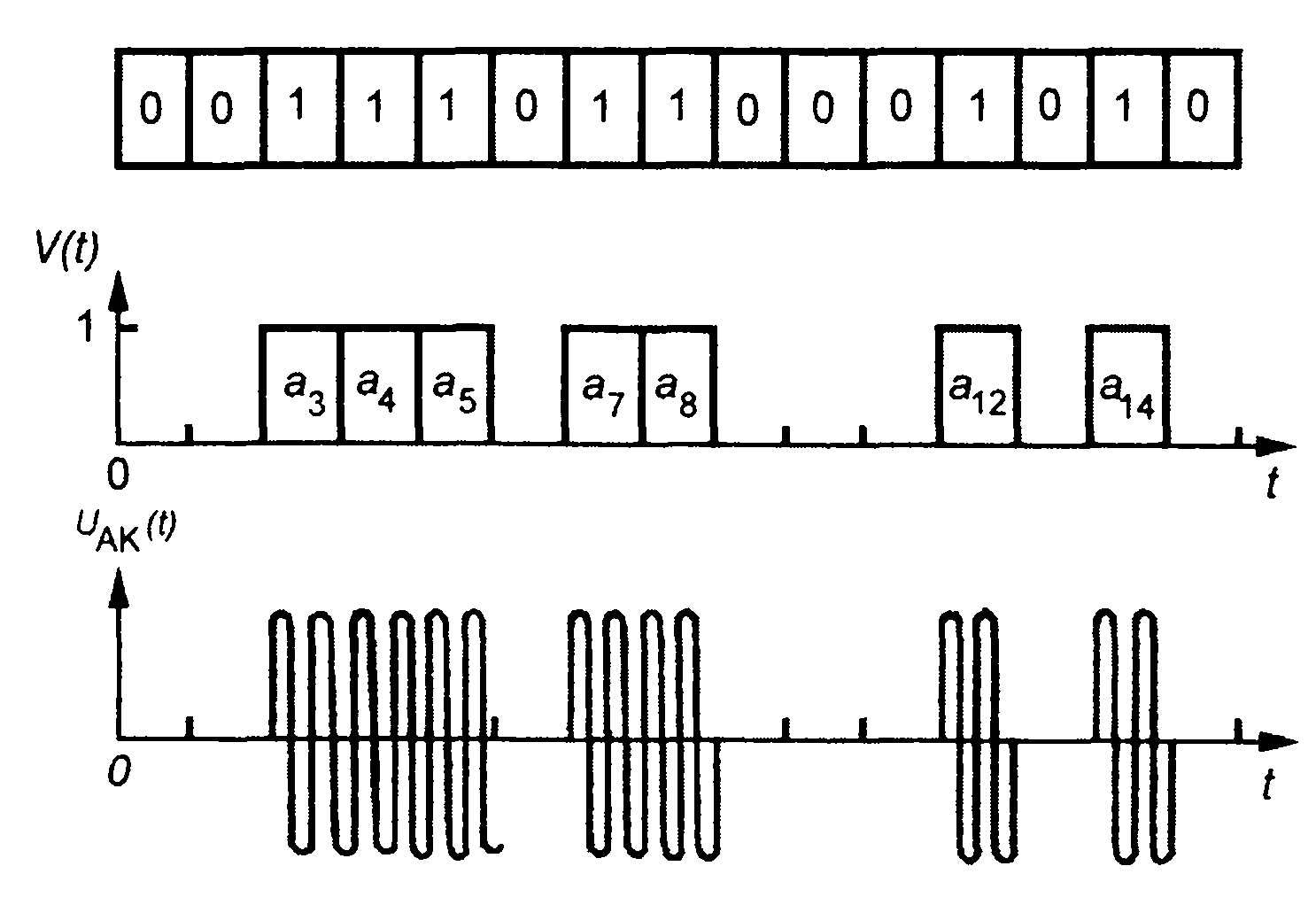
Рис. 12.2

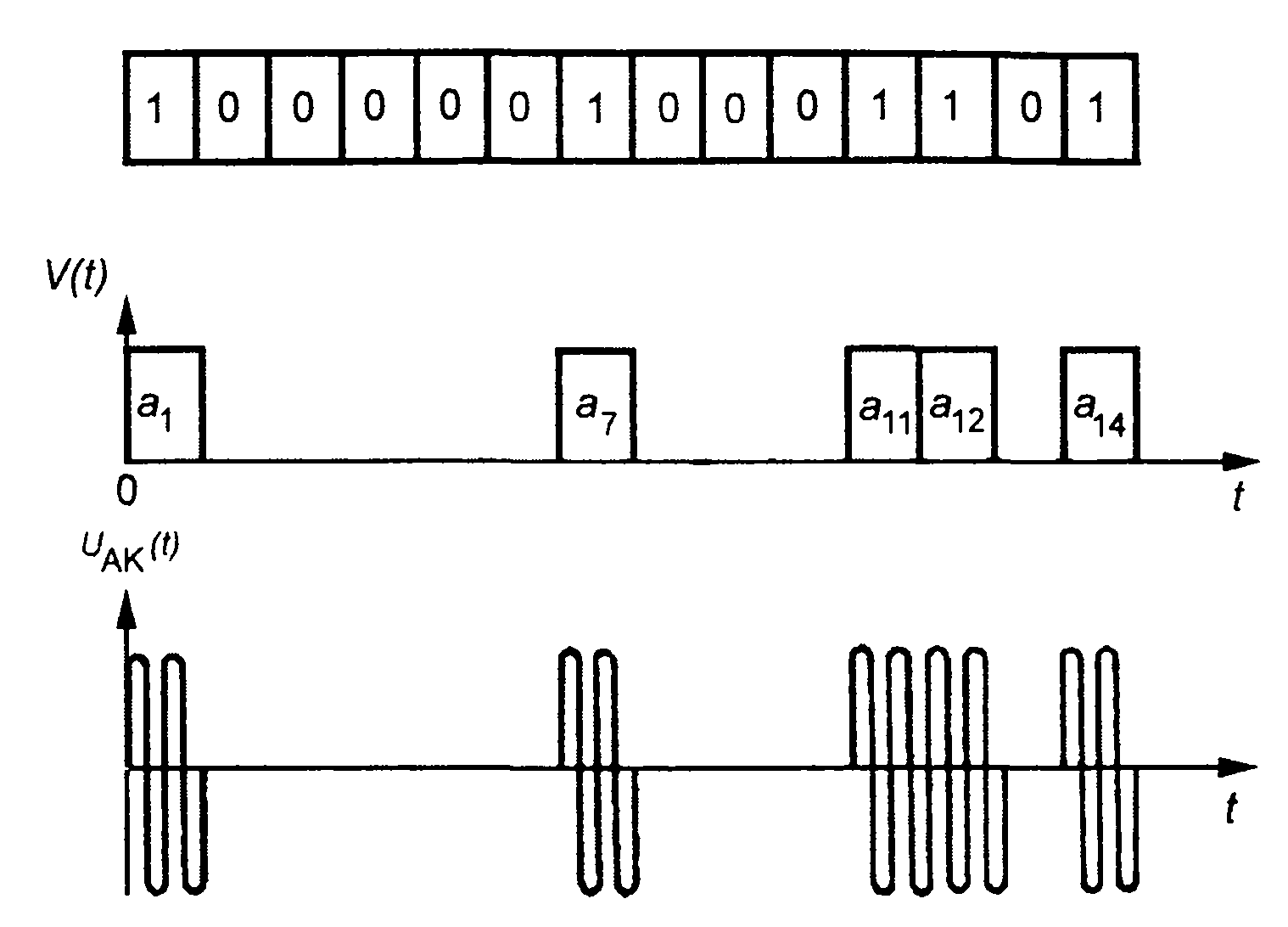
Рис. 12.3

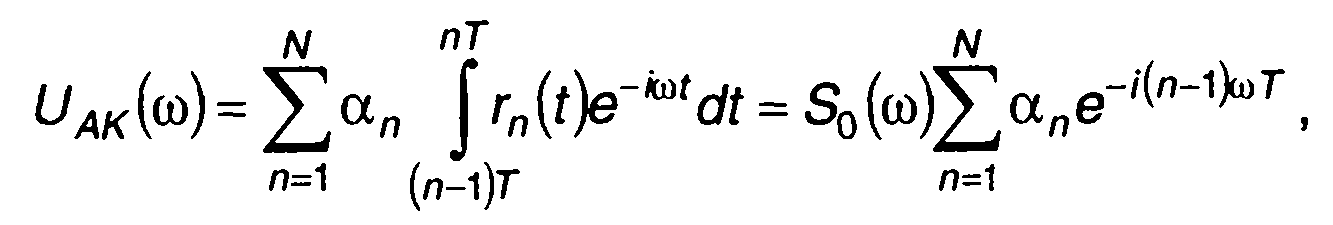(12.11)

где

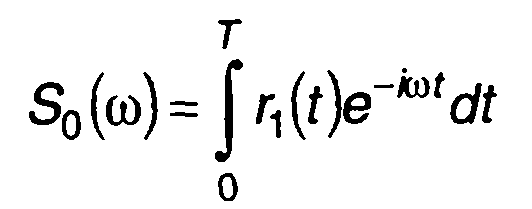(12.12)

- спектральная плотность первого импульса.

Для прямоугольного импульса имеем (разд. 3)

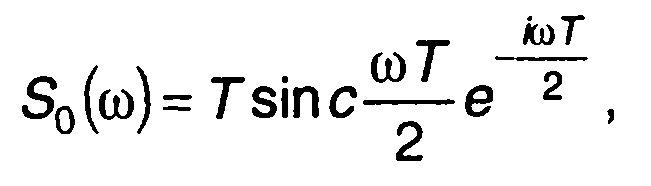(12.13)

Выражение (12.11) запишем в виде

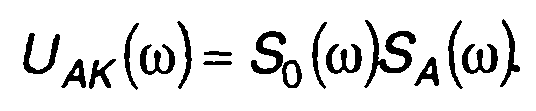(12.14)

Здесь описывает спектральную плотность кодовой последовательности {а_л}

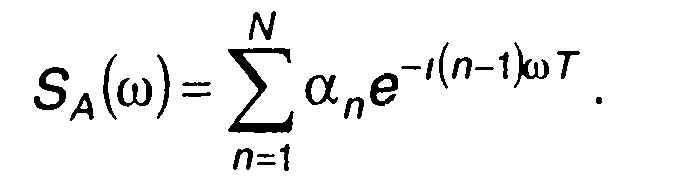(12.15)

Как следует из (12.14), спектр сигнала определяется спектром первого импульса и спектром кодовой последовательности с пе­риодом 2 π/T.

Амплитудный и фазовый спектры комплексной огибающей АК сигнала находятся из (12.14) как

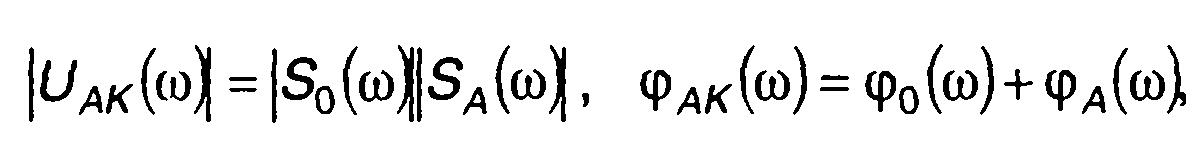(12.16)

где

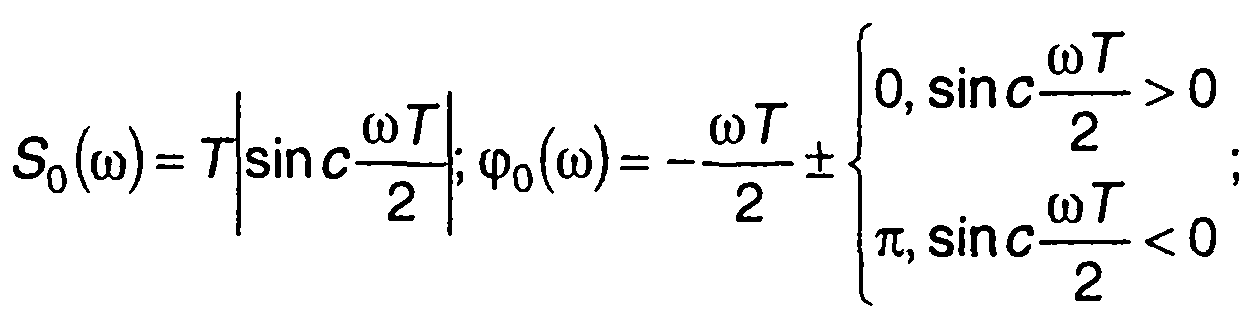(12.17)

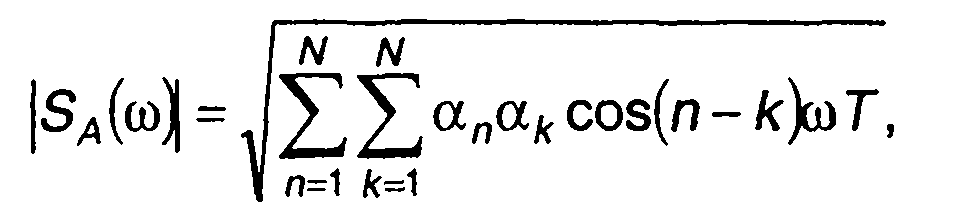(12.18)

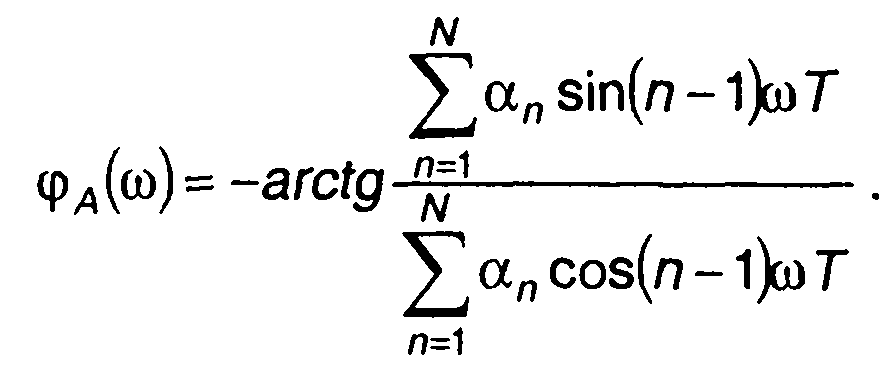(12.19)

Графики амплитудного спектра |S_A(ω)| для кодовых последова­тельностей {а_n} (рис. 12.2 и 12.3) приведены на рис. 12.4,а и 12.5,а. Графики изображены для ω≥0, так как амплитудный спектр симметричен относительно нулевой частоты. Амплитудный спектр кодовой последовательности |S_A(ω)| является периодическим с периодом 2 π/T, имеет осциллирующий характер. Спектр АК сигна­ла представляет результат наложения на спектр прямоугольного импульса (штриховая линия) спектра кодовой последовательности (рис. 12.4,6 и 12.5,6).

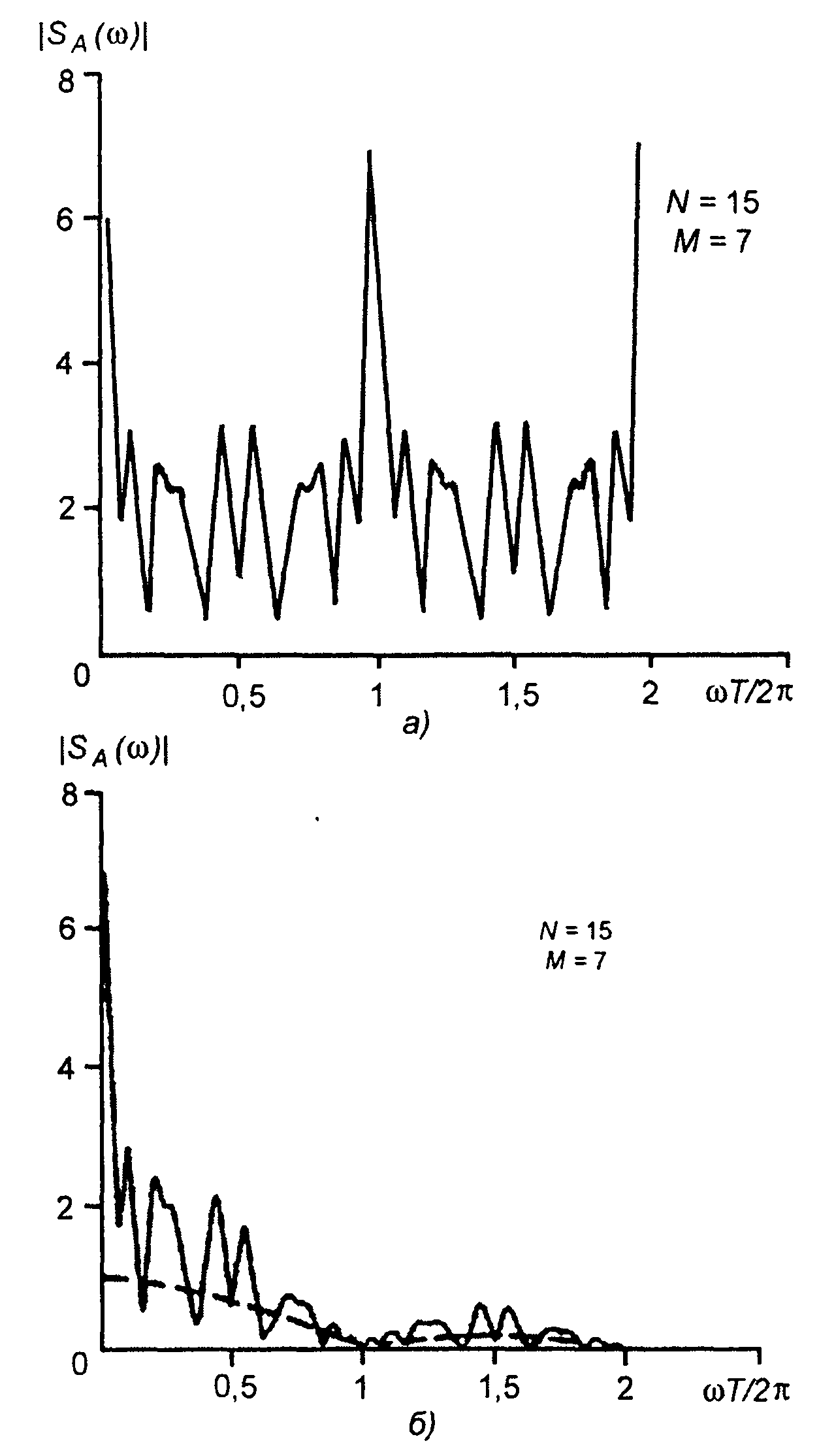
Рис. 12.4

При ω = 0 значения амплитудных спектров равны

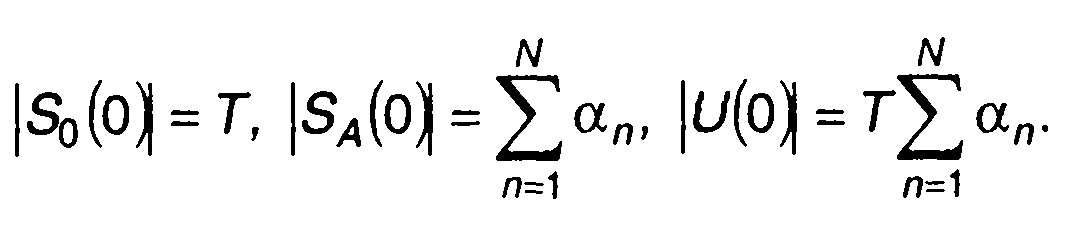
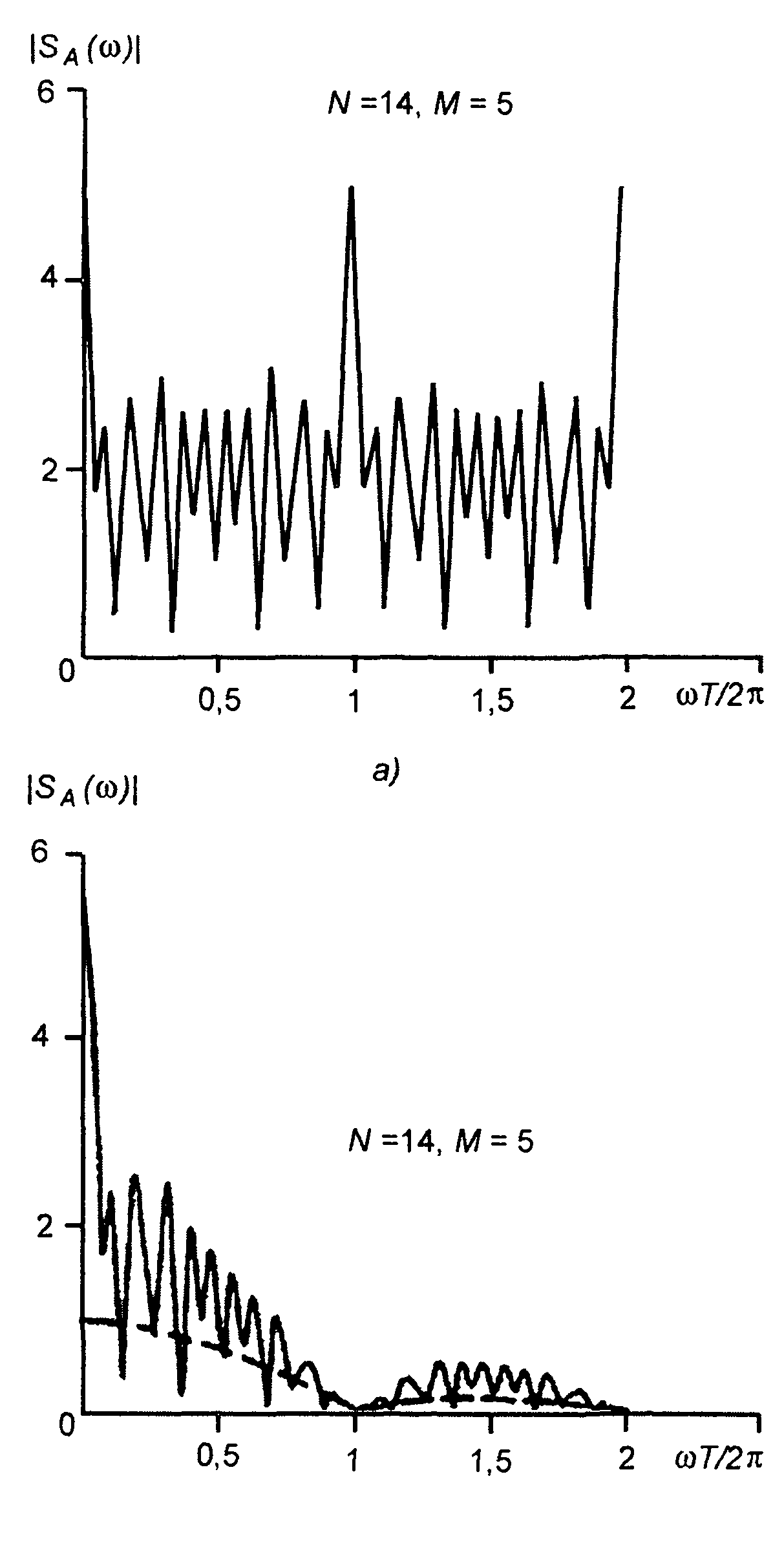
б)

Рис. 12.5

Для двоичной кодовой последовательности, имеющей М еди­ниц,

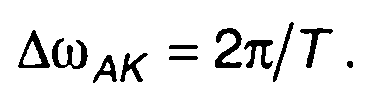
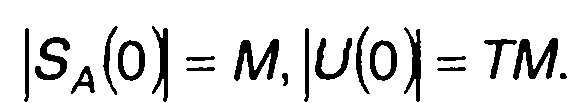
Ширина спектра АК сигнала может быть определении как

База АК сигнала - произведение длительности сигнала NT на ширину спектра ∆ω_АК

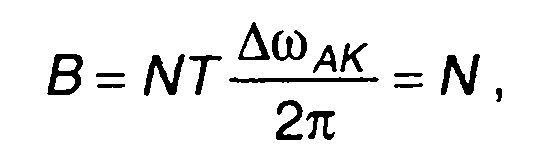(12.20)

равна длине кодовой последовательности.

12.2.2. Корреляционная функция комплексной огибающей АК сигнала

Корреляционная функция комплексной огибающей АК сигнала определяется (13.8) с подстановкой в него (13.10)

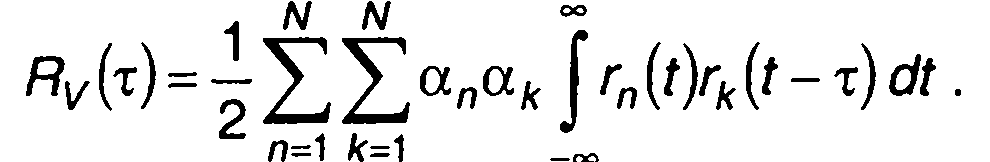(12.21)

Интеграл в (12.21) с учетом (12.2) запишется в виде

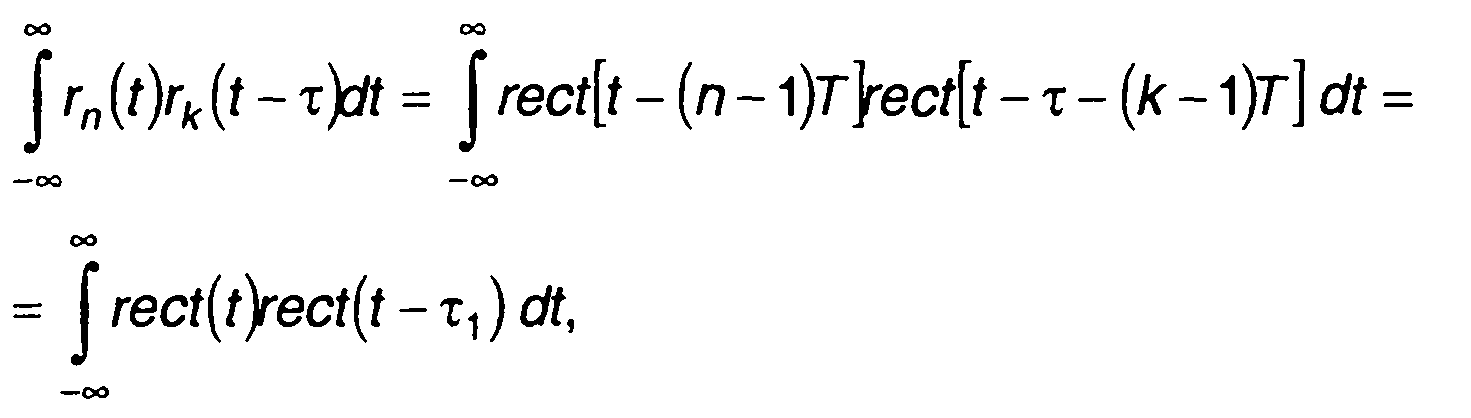(12.22)

где

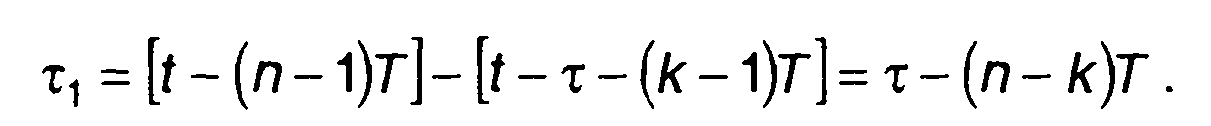(12.23)

Вводя корреляционную функцию одиночного импульса

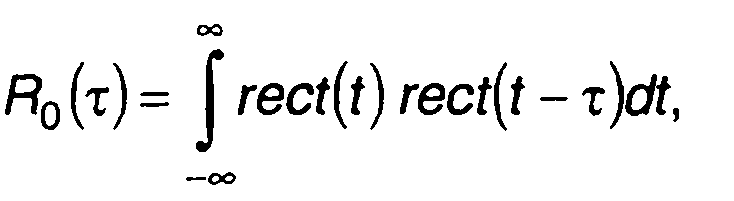(12.24)

выражение (12.21) перепишем в виде

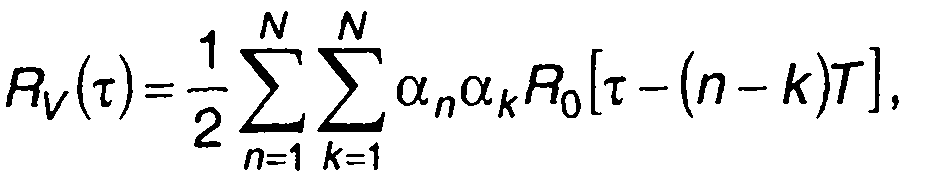(12.25)

где все а_n и а_k, индексы которых находятся вне диапазона {1,2,...,N}, равны нулю.

Замена в (12.25) индекса суммирования на т-n-k приводит к выражению для R_v(τ) в виде

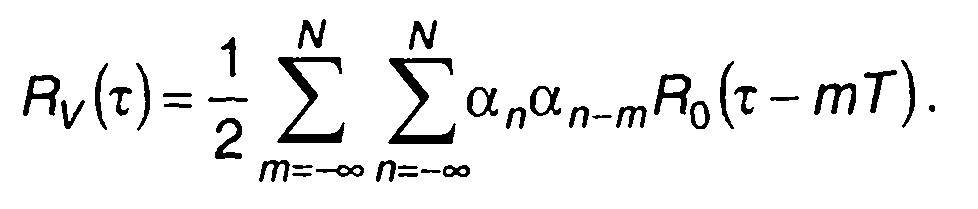(12.26)

Величина

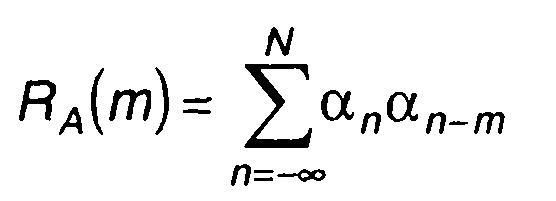(12.27)

представляет корреляционную функцию кодовой последователь­ности. В (12.27) все а_n,а_n-m с индексами вне диапазона {1,2,..., N]

равны нулю. Подставляя (12.27) в (12.26), получим

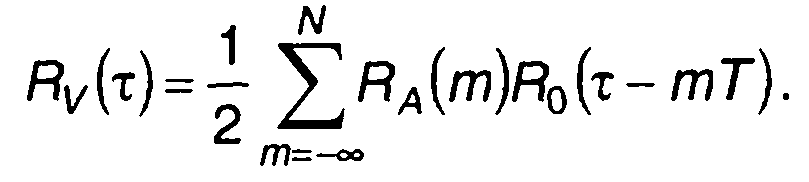(12.28)

Очевидно, что R_A(m) = 0 при m≥N и m≤-N. С учетом этого

выражение для корреляционной функции может быть записано в виде

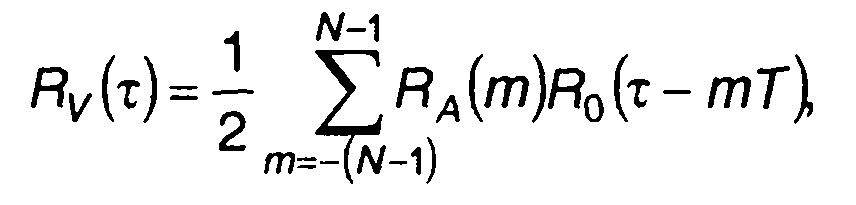(12.29)

где

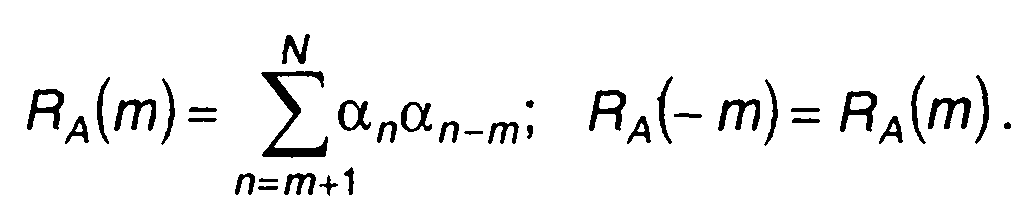(12.30)

Выражения (12.29) и (12.30) показывают, что корреляционная функция комплексной огибающей АК сигнала представляет сумму повторяющихся с интервалом Т корреляционных функций

одиночного импульса (12.24), максимальные значения, которых определяются корреляционной функцией кодовой последовательности R_А(т).

Для прямоугольного импульса (разд. 5)

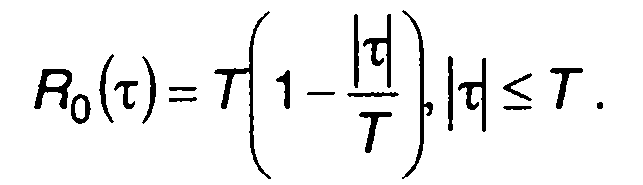(12.31)

При т = О

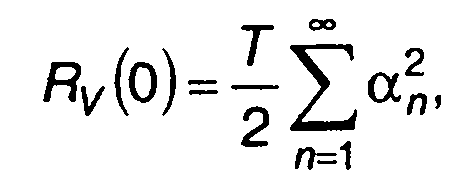(12.32)

для двоичной кодовой последовательности

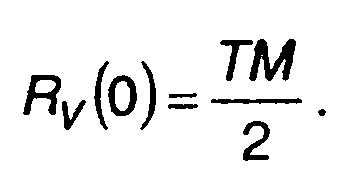(12.33)

При значениях т = тТ

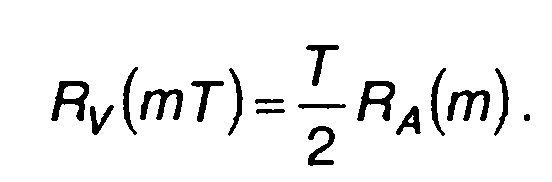(12.34)

На рис. 12.6 приведены графики корреляционных функций R_v(т) для АК сигналов, изображенных на рис. 12.2 и 12.3 (для

т > 0). Корреляционные функции получены как результат наложе­ния треугольных импульсов (12.31), обозначенных на рисунке штриховыми линиями, с амплитудами (12.34), длительностью 2T, следующих с интервалом Т.

12.3. Фазо-кодированные сигналы

12.3.1. Описание ФК сигнала

Фазо-кодированный сигнал представляет последовательность прямоугольных радиоимпульсов с одинаковыми амплитудами и получается в результате модуляции фазы гармонического несу­щего колебания кодовым сигналом (последовательностью).

Они описываются выражением

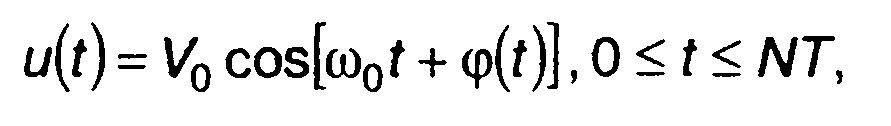(12.35)

или в комплексной форме

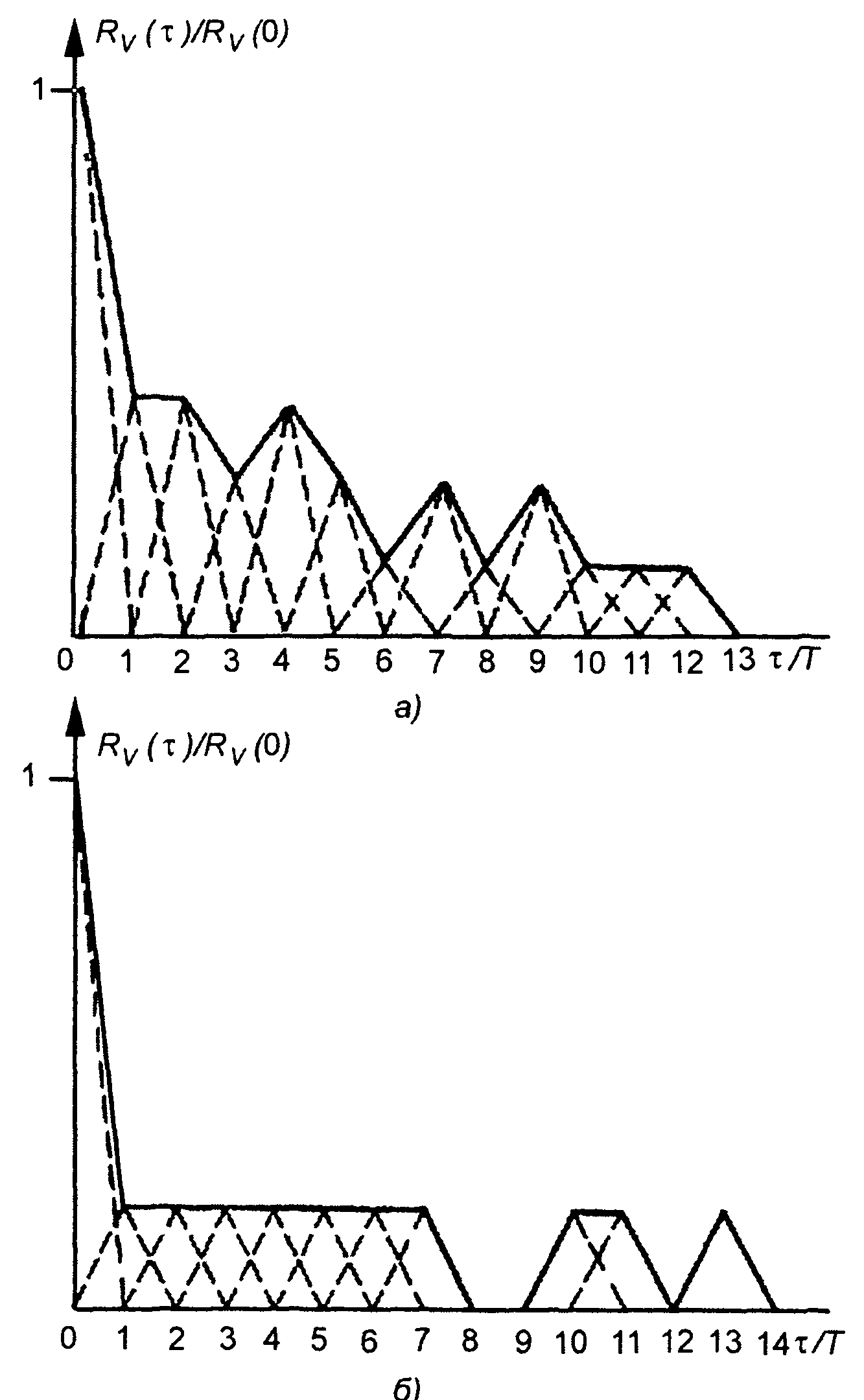
Рис. 12.6

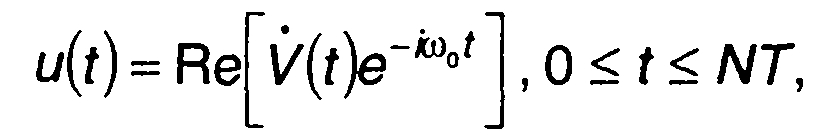(12.36)

где 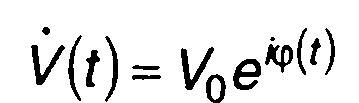- комплексная огибающая кодированного сигнала;

V₀,ω_о,φ(t) - амплитуда, несущая частота и фаза сигнала; Т - дли­тельность одного импульса; N - число радиоимпульсов кодирован­ного сигнала.

За время одного импульса фаза может быть постоянной, меня­ясь скачком от импульса к импульсу. Кодированный сигнал в этом случае представляет гармоническое колебание с фазовой манипу­ляцией (рис.12.7).

Возможны сигналы с фазой, непрерывно изменяющейся в течение определенного интервала времени - сигналы с непрерывной фазой. Появление таких сигналов связано прежде всего со стремлением по­лучить лучшие спектральные характеристики сигнала, обеспечивающие более высокое качество передачи информации и помехоустойчивость системы.

В общем случае выражение для фазы кодированного сигнала на одном интервале записывается в виде

где {с_k} - кодовая последовательность; h_k называют индексом модуляции на k-м интервале.

Различают сигналы с постоянным индексом модуляции и с цик­лически изменяющимся индексом модуляции. Функция q(t) в (12.37) называется фазовым импульсом. На интервале [0,17] она изменяется от 0 до 1/2 L - длина фазового импульса (часто L = 1). Фаза при этом изменяется в пределах πc_kh_k .

Выражение для частоты сигнала запишется в виде

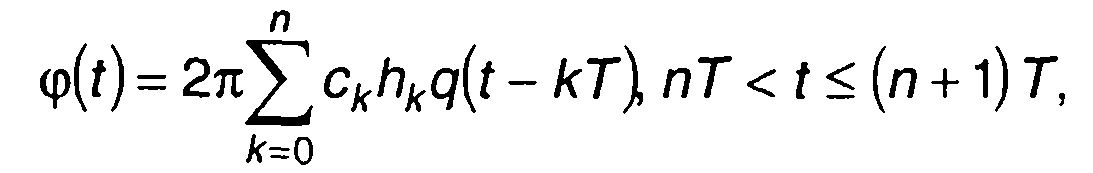(12.37)

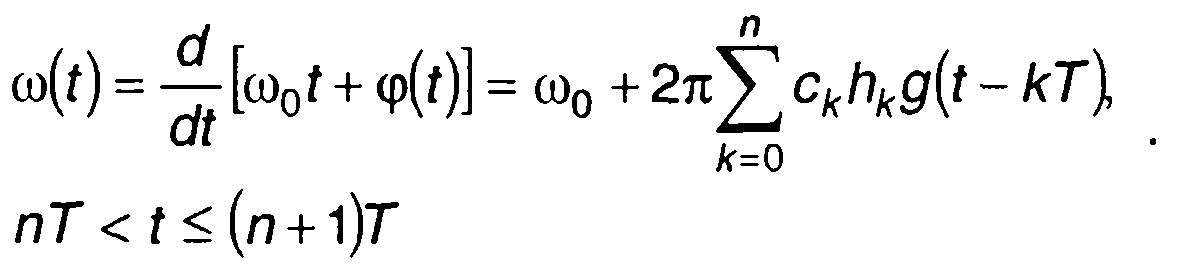(12.38)

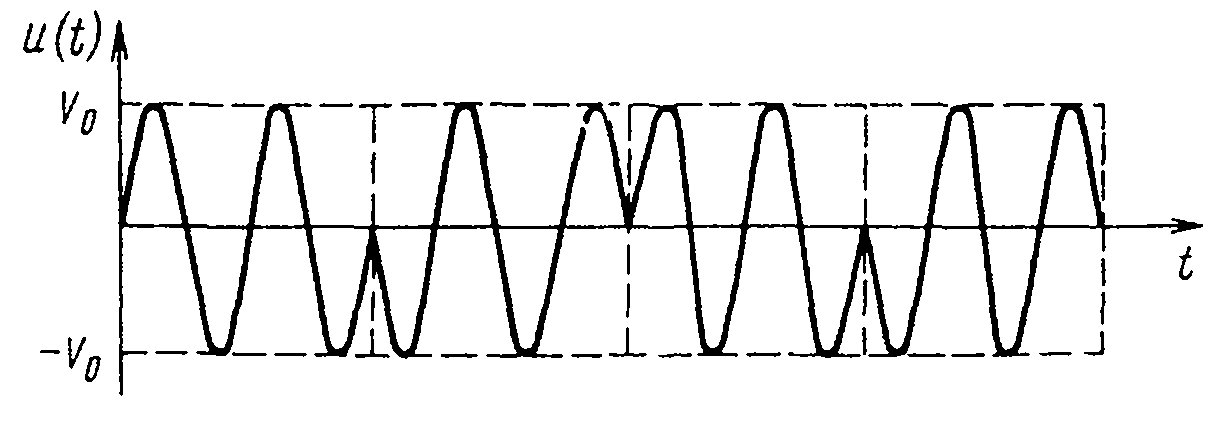
Рис.12.7

Функция g(t) описывает частотный импульс. Его длительность равна LT. На рис. 12.8 изображены графики некоторых видов фазовых и частотных импульсов. На рис. 12.8,а приведен график сту­пенчатой функции, на рис. 12.8,6 - линейной функции q(t). Линей­ной зависимости q(t) соответствует ступенчатая функция g(t) - частотная манипуляция. Более плавное изменение фазы может быть описано различными функциями. Примером такой зависимо­сти является зависимость, описываемая тригонометрической функцией (рис. 12.8,в) 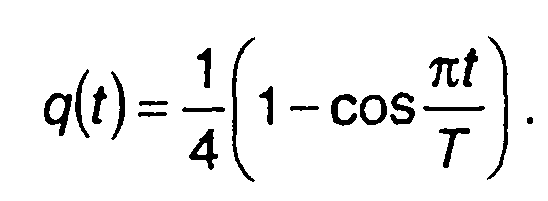(12.39)

Изменение фазы сигнала во времени поясняется фазовой диа­граммой (рис. 12.9). График на рис. 12.9 иллюстрирует возможные φ(t) изменения функции φ(t), описываемой линейной (более тонкие линии) и тригонометрической функциями.

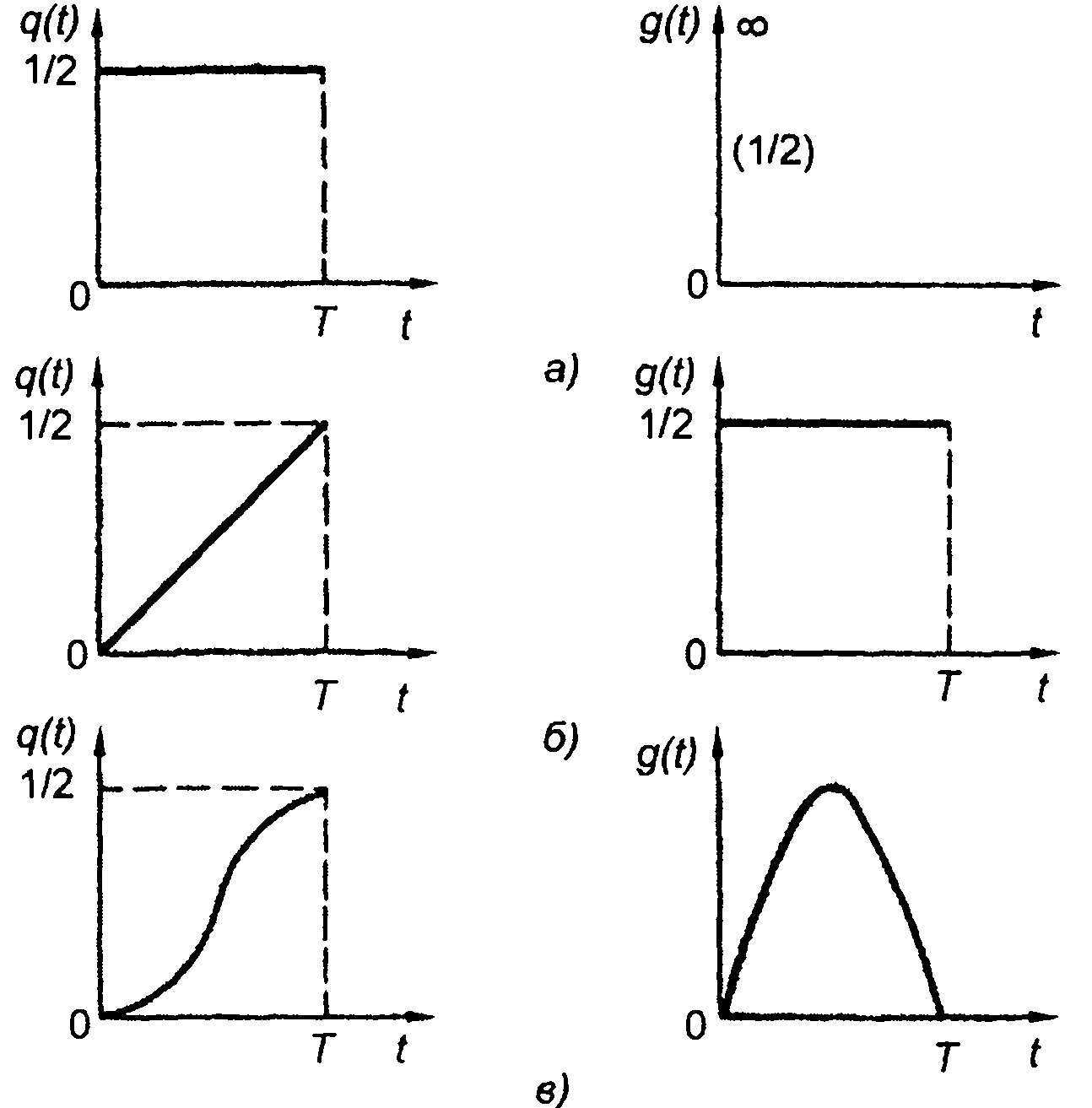
Рис. 12.8

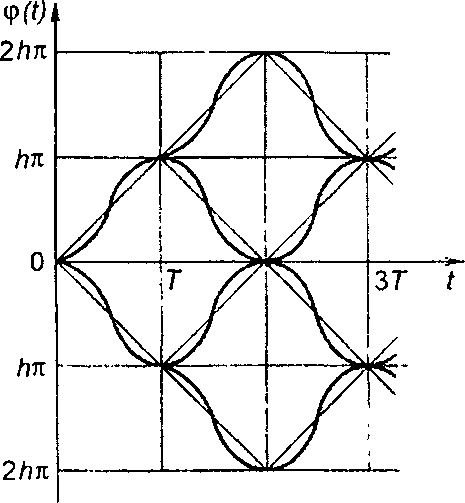
Рис. 12.9

Характеристики ФК сигналов удобнее определять через харак­теристики их комплексных огибающих: спектральная плотность

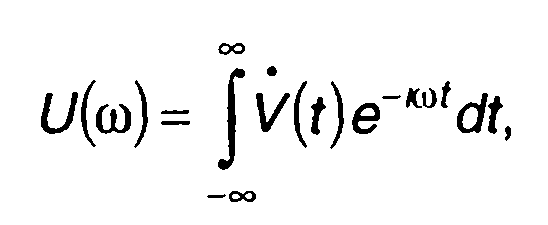(12.40)

корреляционная функция

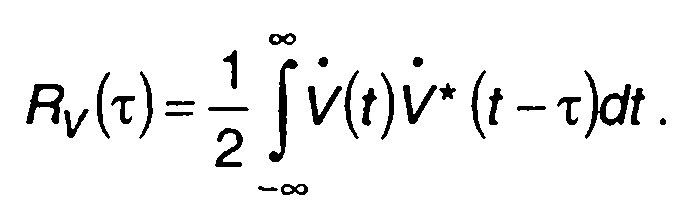(12.41)

Указанные характеристики при различных законах изменения фазы: скачкообразном и линейном (скачкообразный закон измене­ния частоты) и описываемом тригонометрической функцией, опре­делены в [16]. Ниже рассматриваются характеристики ФК сигнала только со скачкообразным изменением фазы и частоты.

12.3.2. Спектр ФК сигнала со скачкообразным изменением фазы

Сигналы со скачкообразным изменением фазы нашли практиче­ское применение в радиолокации, связи, системах управления и других областях техники. Кодированный сигнал представляет

последовательность радиоимпульсов, у которых от импульса к им­пульсу скачком изменяется только фаза φ_n.

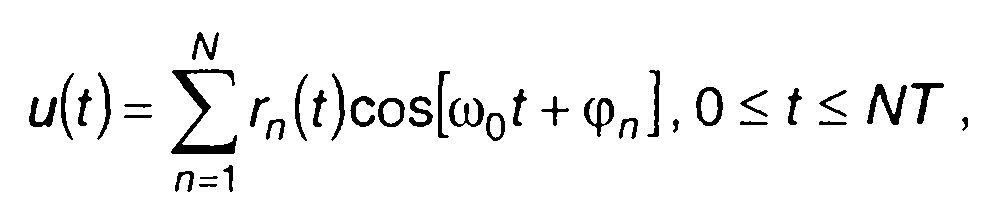(12.42)

где r_n(t) - огибающая одиночного, как правило, прямоугольного импульса.

Кодовая последовательность {φ_n} задает закон изменения фа­зы. Комплексную огибающую сигнала удобнее представить в виде

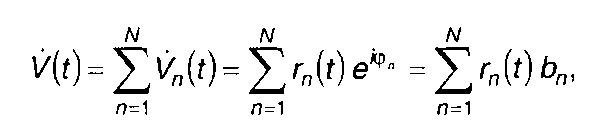(12.43)

где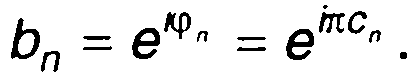

При использовании бинарного кода фаза принимает значение 0 или π. В этом случае:

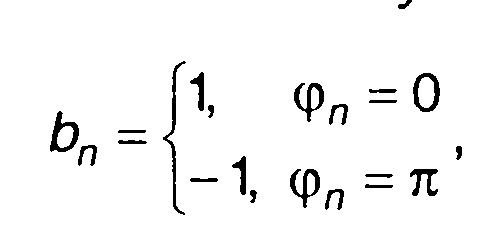
Спектральная плотность комплексной огибающей ФК сигнала может быть определена из (12.40) подстановкой (12.43). При r_n(t)= 1 имеем

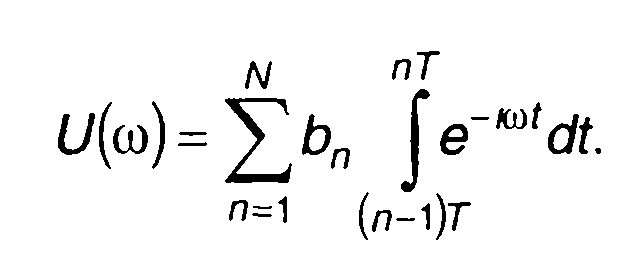(12.44)

Спектральная плотность последовательности импульсов опре­деляется как сумма спектральных плотностей идентичных по фор­ме импульсов, смещенных во времени каждый относительно пре­дыдущего на интервал времени Т. Используя свойства преобра­зования Фурье, (12.44) запишем в виде

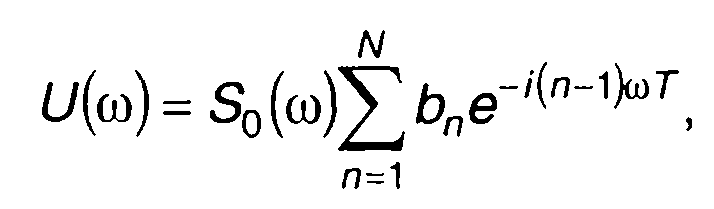(12.45)

где

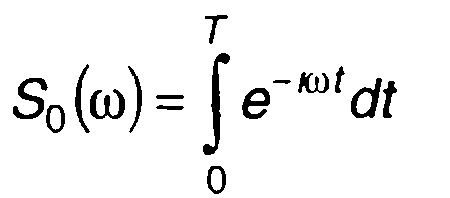
- спектральная плотность первого импульса.

Для прямоугольного импульса

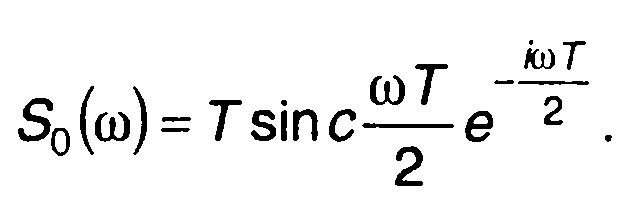(12.46)

Выражение для U(ω) перепишем в виде

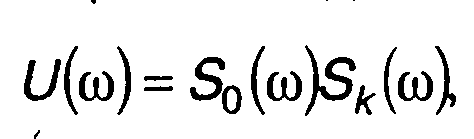(13.47)

где

- спектральная плотность кодовой последовательности.

Квадрат модуля кодовой последовательности определим из

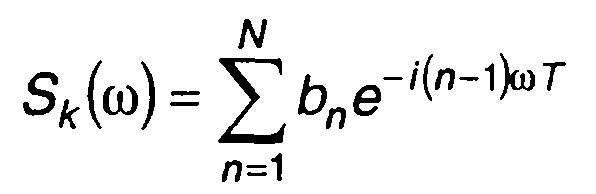(12.48)

как

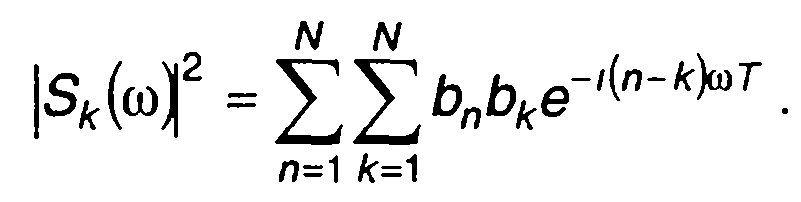(12.49)

Используя формулу Эйлера и учитывая, что косинус является четной функцией, а синус - нечетной, из (12.49) получим

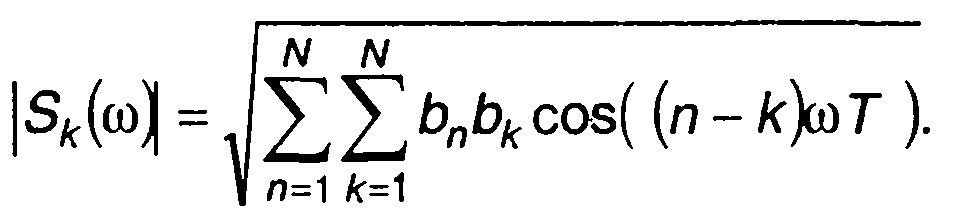(12.50)

Выражение для фазового спектра найдется из (12.48) в виде

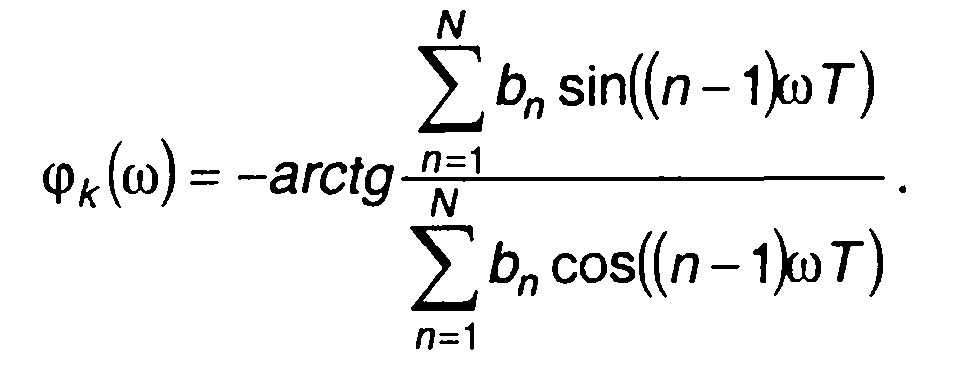(12.51)

Амплитудный спектр комплексной огибающей получается из (12.47) как произведение модулей |S₀(ω)| и \S_k(ω)|

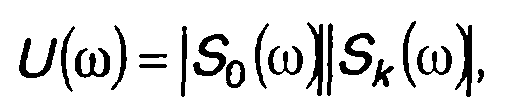(12.52)

а фазовый спектр - как сумма аргументов φ₀(ω) и φ_k(ω):

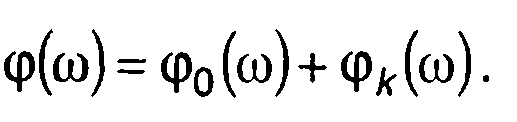(12.53)

График амплитудного спектра сигнала, модулированного кодо­вым сигналом, изображенным на рис. 12.1, приведен на рис. 12.10,6.

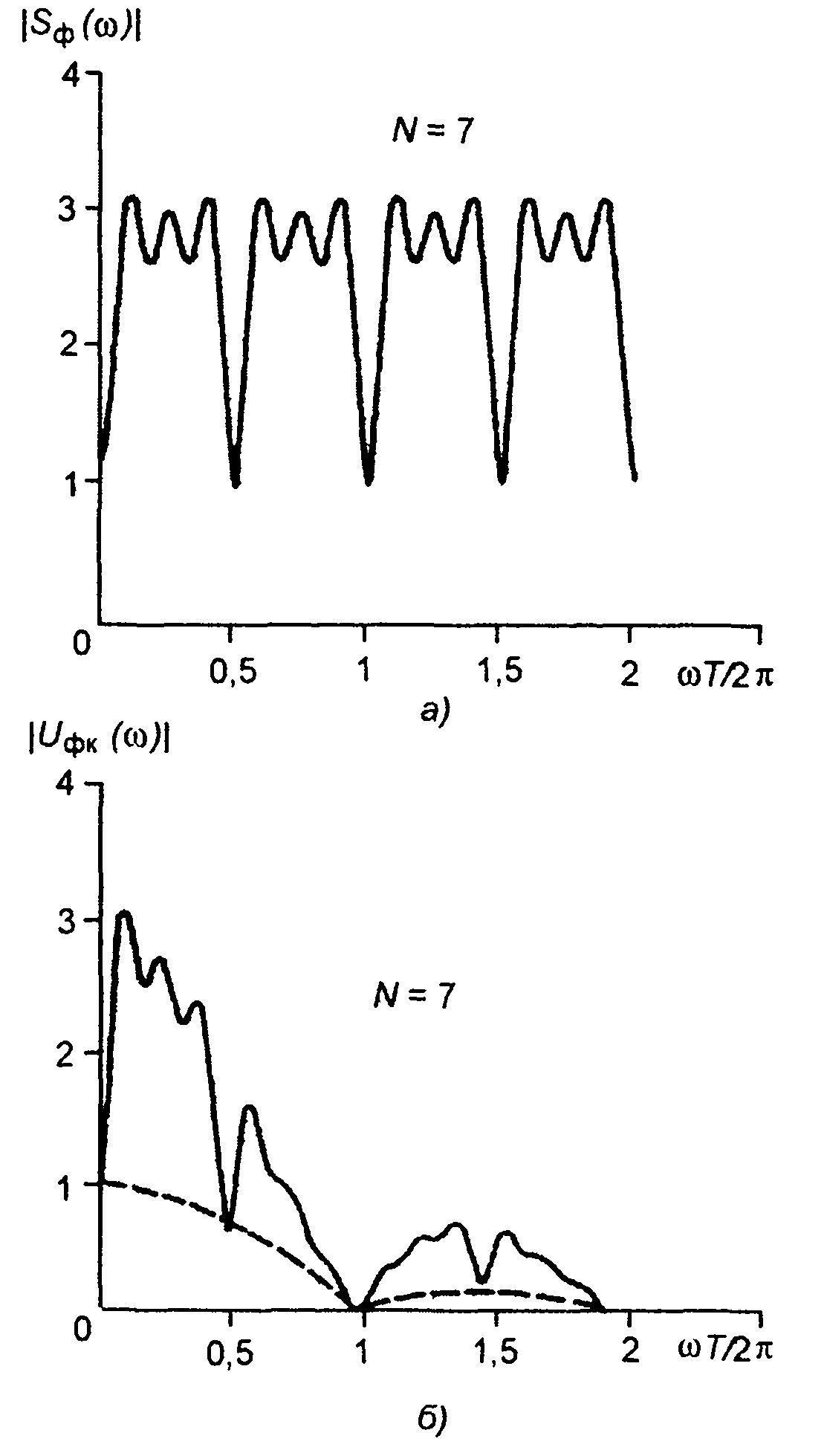
Рис. 12.10

Спектр комплексной огибающей сигнала представляет резуль­тат перемножения амплитудного спектра прямоугольного импульса (штриховая линия) и амплитудного спектра кодовой последова­тельности (рис. 12.10,а).

При ω = 0 имеем

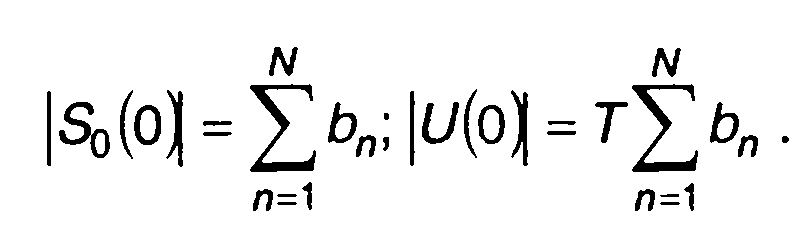(12.54)

Ширину спектра определим как

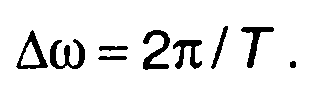(13.55)

Произведение длительности сигнала и ширины его спектра - база сигнала, равна

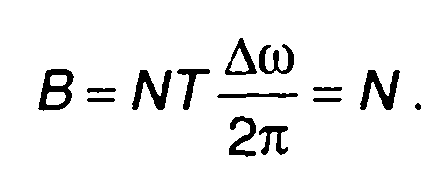(12.56)

Таким образом, база рассматриваемого ФК сигнала определя­ется длиной кодовой последовательности.

12.3.3. Корреляционная функция ФК сигнала со скачкообразным изменением фазы

Корреляционная функция комплексной огибающей ФК сигнала определяется (12.41) с учетом (12.43)

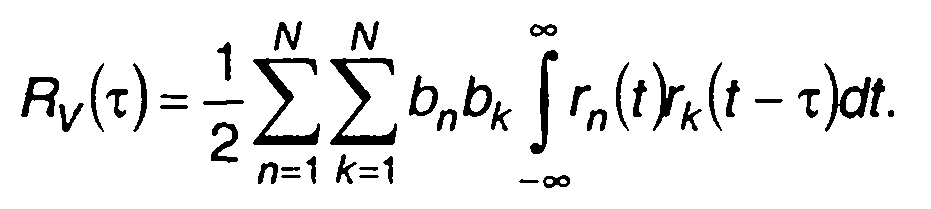(12.57)

Интеграл в (12.57) запишем в виде

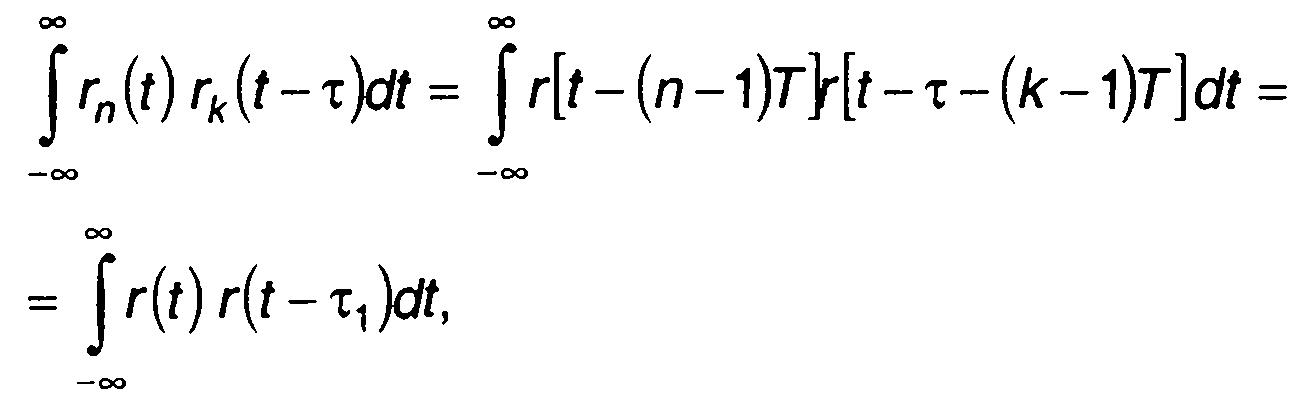(12.58)

где r(t) - огибающая одиночного импульса,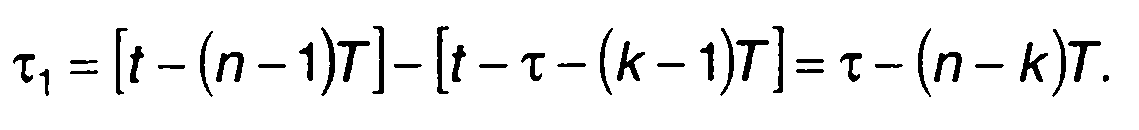

Обозначим R₀(т) корреляционную функцию одиночного им­пульса,

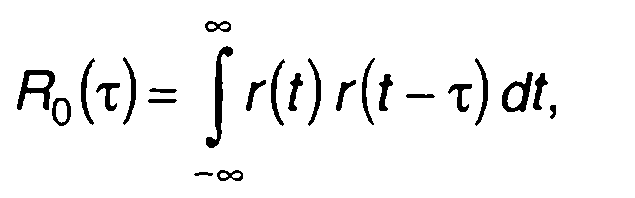(12.59)

а выражение (13.57) запишем в виде

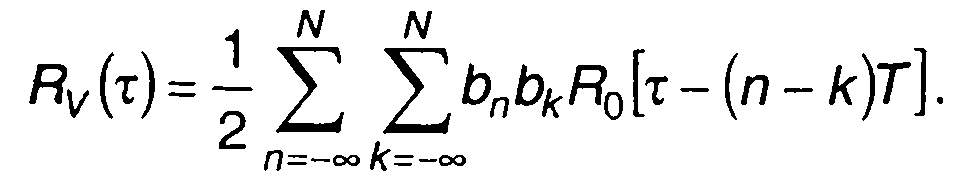(12.60)

В (12.60) все b_n и b_k, индексы которых находятся вне диапазо­на {1,2,..., N}, равны нулю. Произведя замену индекса суммирова­ния т = n- к, запишем

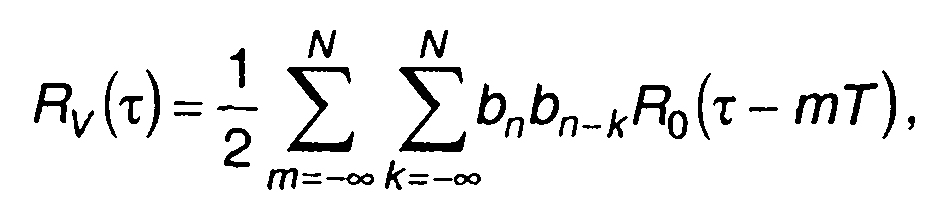(12.61)

В (12.61)

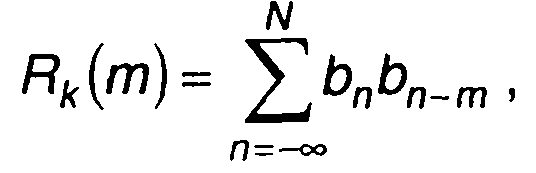(12.62)

представляет корреляционную функцию кодовой последовательности. С учетом (12.62) получим

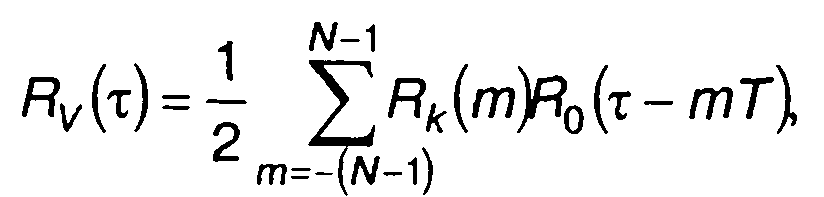(12.63)

Функция R_k(m) - четная, т.е.

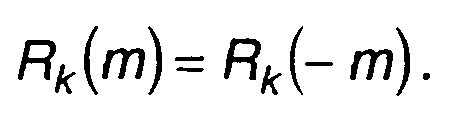(12.64)

Обычно импульсы кодированного сигнала имеют прямоуголь­ную форму

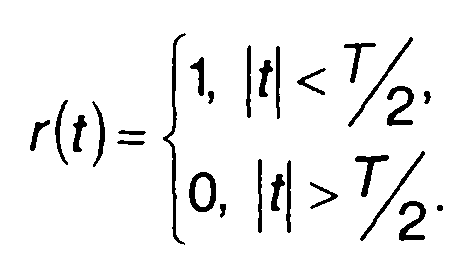(12.65)

В этом случае

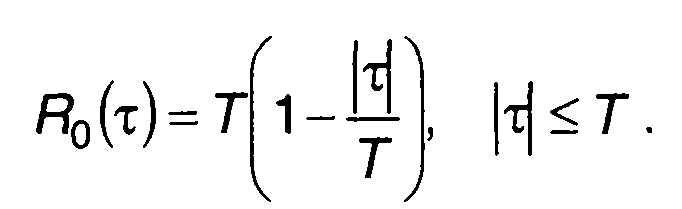(12.66)

Как следует из (12.61) и (12.62), корреляционная функция ком­плексной огибающей ФК сигнала представляет сумму корреляци­онных функций одиночных импульсов, максимальные значения которых определяются значениями корреляционных функций ко­довой последовательности.

При т = 0

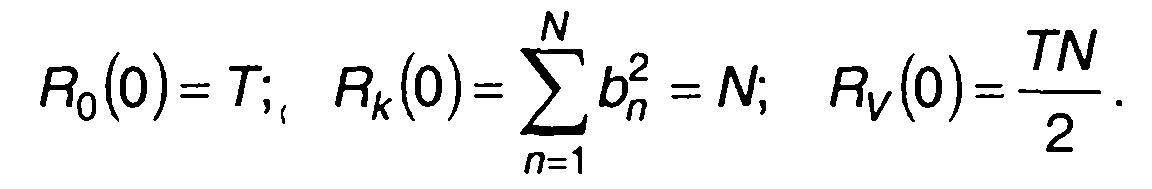(12.67)

При т = тТ

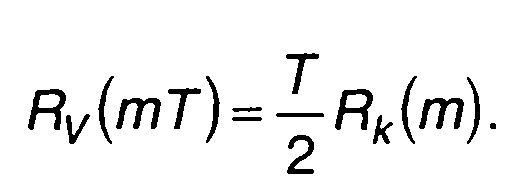(12.68)

Для бинарных кодов функцию R_k{m) удобно определять сле­дующим образом [40]. Составляется таблица с верхней строкой, описывающей кодовую последовательность {b_n}, и левым столб­цом, описывающим ту же кодовую последовательность, если, чи­тать ее сверху вниз {b__n}, рис. 12.11. В средней части таблицы за­писывается результат перемножения элементов {b_n} и {b__n}. При этом, если элемент {b__n} имеет знак плюс, то элемент {b_n} запи­сывается в строку без изменения, если знак минус - то со сменой знаков всех элементов. Запись производится со смещением на один элемент вправо по отношению к предыдущей строке. Сумма элементов каждого вертикального столбца дает значение R_k(m).

На рис. 12.11 составлена таблица, а по результатам расчета по­строен график корреляционной функции комплексной огибающей ФК сигнала, промодулированного кодовой последовательностью, изображенной на рис. 12.1.

12.3.4. Коды Баркера

Кодовые сигналы, используемые при фазовой модуляции, могут быть самыми разнообразными. Их выбор зависит в первую оче­редь от того, в какой радиотехнической системе используется

сигнал, какие функции выполняет система. Не проводя анализа воз­можных видов кодов, используемых при угловой модуляции, оста­новимся на наиболее известных и рассмотрим их как иллюстрацию общих положений.

В радиолокации хорошо известны коды Баркера и М-после- до- вательности. Модуляция ими высокочастотных сигналов обеспечи­вает высокую разрешающую способность системы. Корреляцион­ная функция кодированных сигналов имеет узкий центральный пик и напоминает корреляционную функцию шума. Такие сигналы на­зываются шумоподобными.

Коды Баркера {b_n} определяются как двоичные последователь­ности, имеющие корреляционную функцию вида

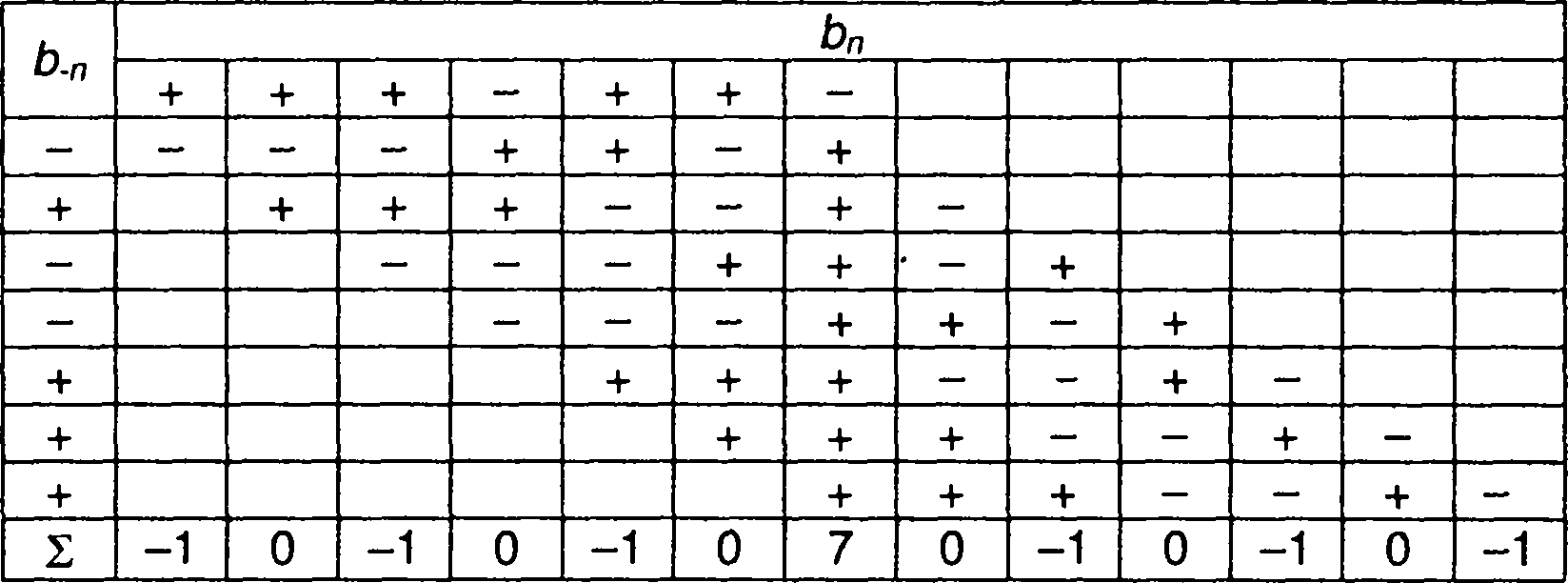
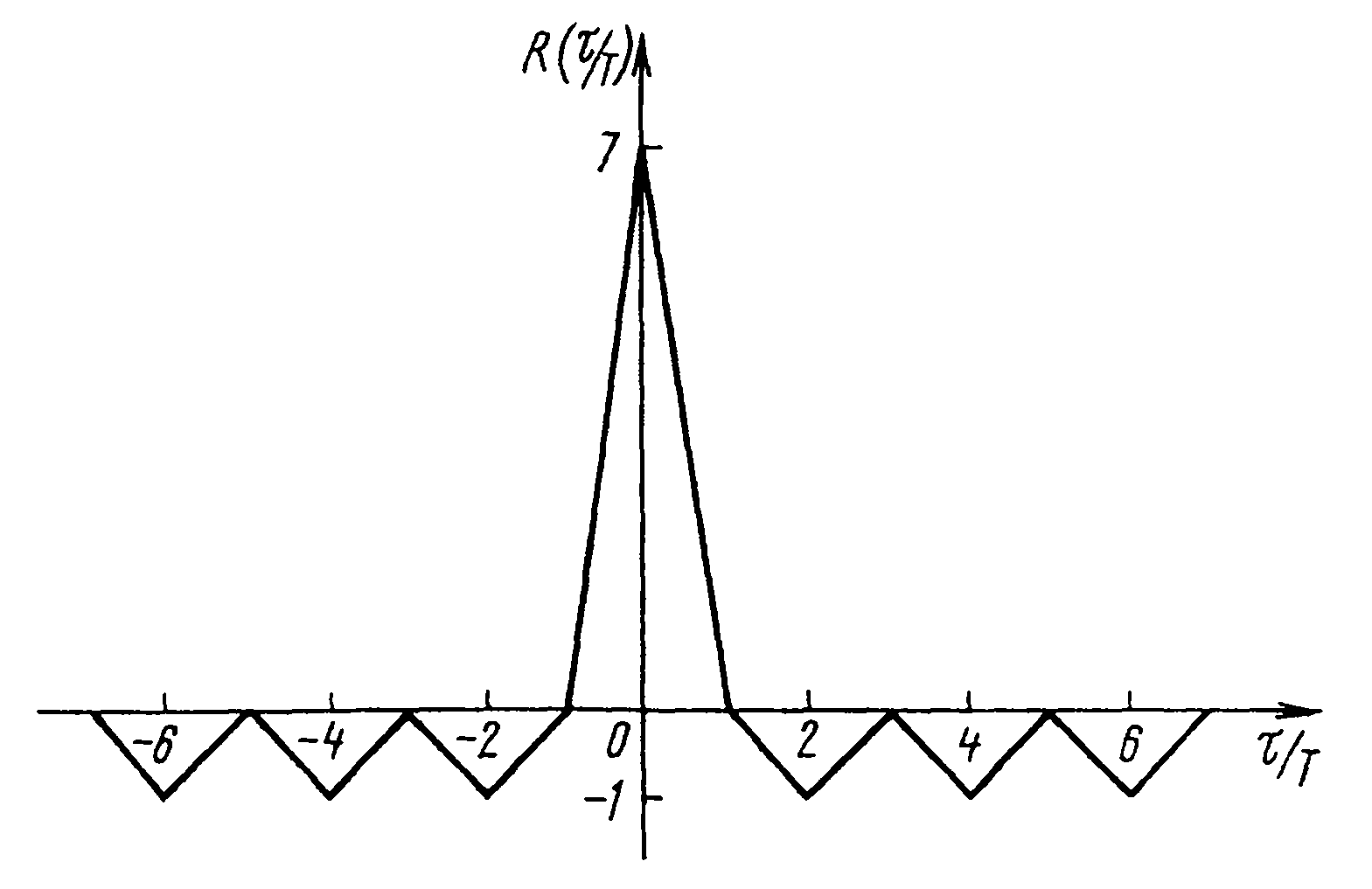
Рис. 12.11

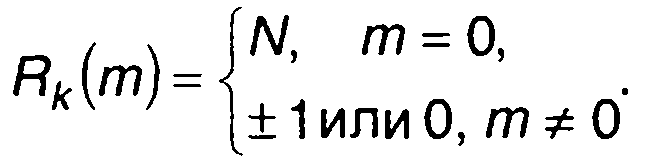(12.69)

Существует всего девять кодов Баркера (табл. 12.1).

Таблица 12.1

Коды Баркера

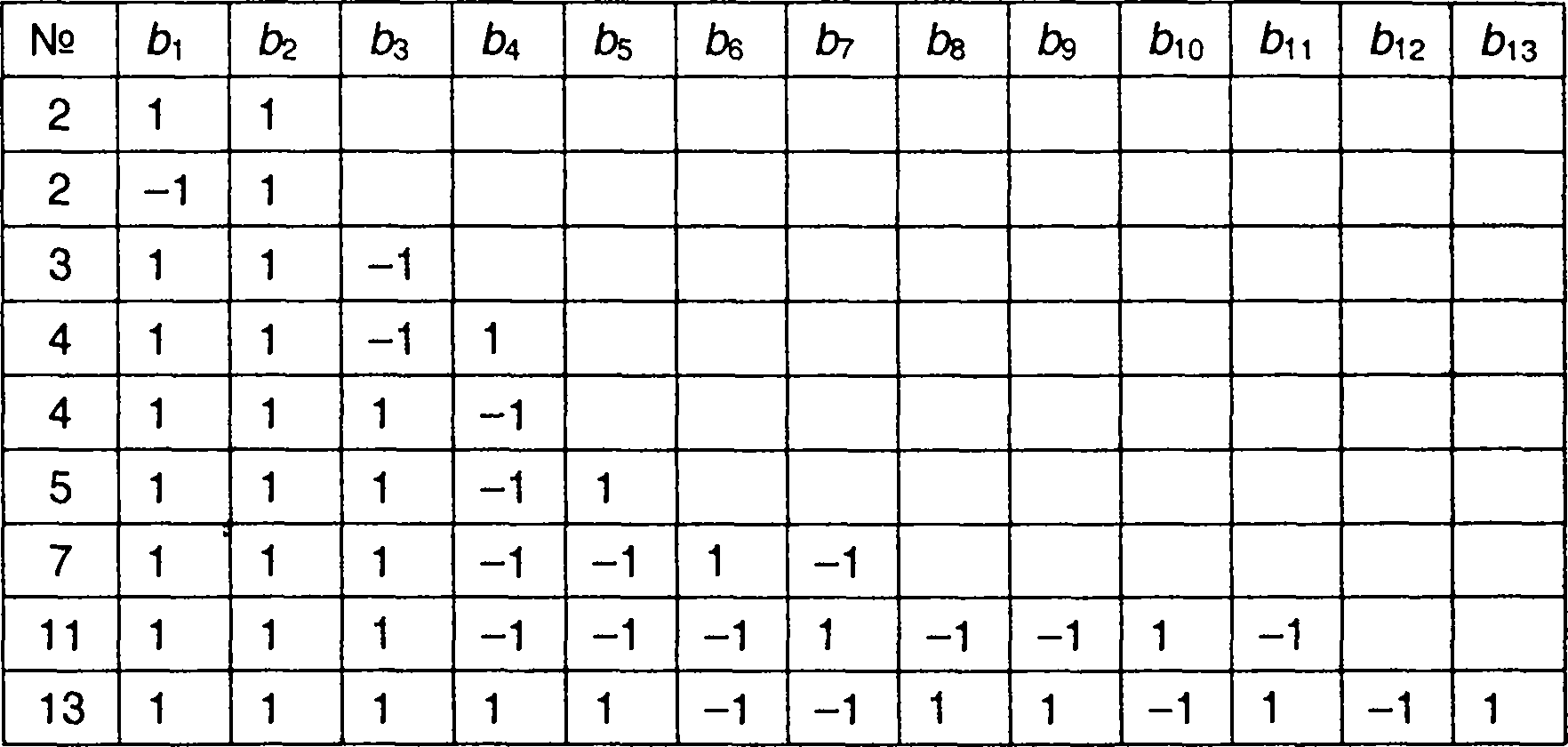
Определив корреляционную функцию кода Баркера, найдем со­ответствующую спектральную плотность энергии

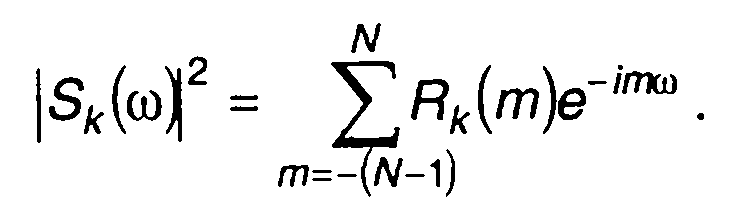(12.70)

Функция R_k{m) является четной. С учетом этого и (12.69) выра­жение (12.70) запишем в виде

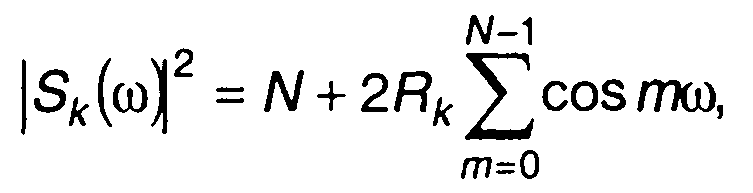(12.71)

где R_k=±1.

Используя известное соотношение [12]

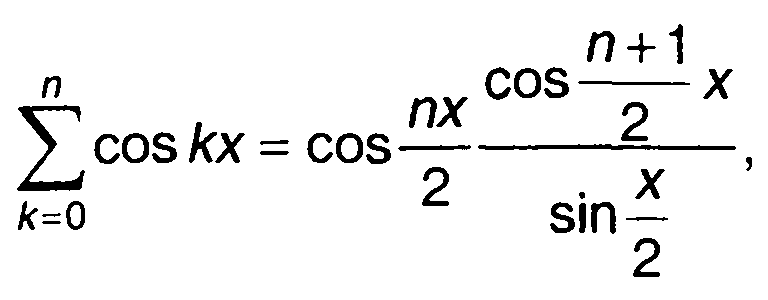(12.72)

выражение для |S_k(ω)|² представим в виде

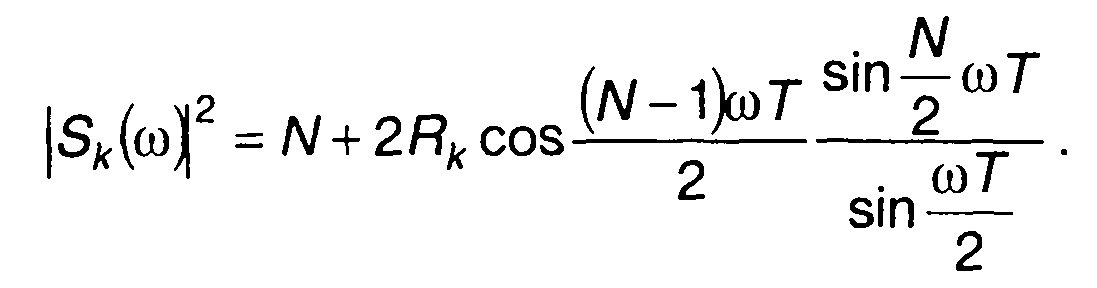(12.73)

При R_k = 1 (коды с N , равным 4,5,13)

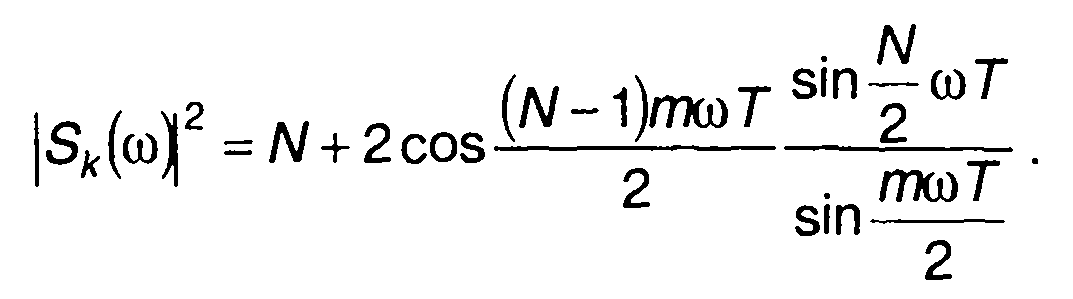(12.74)

При R_k = —1 (коды с N , равным 3,4,7,11)

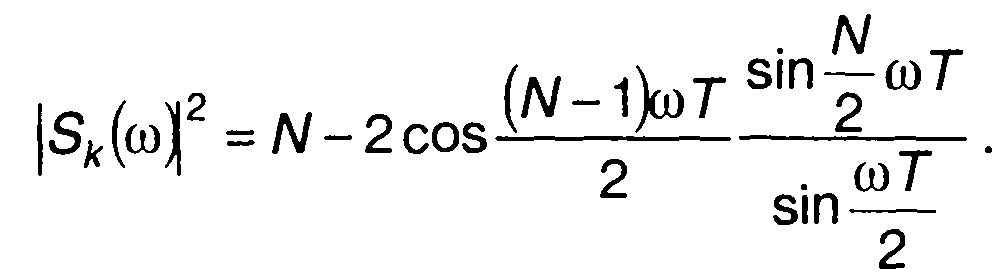(12.75)

Корреляционные функции комплексных огибающих сигналов с кодами Баркера определяются (12.63), их графики приведены в [15]; там же приведены графики амплитудных спектров комплекс­ных огибающих сигналов.

12.3.5. M-последовательности

Из кодовых последовательностей, нашедших практическое применение, особое место занимают последовательности, полу­чаемые с помощью генераторов, выполненных на регистрах сдви­га; из них в первую очередь - линейные последовательности мак­симальной длины или /W-последовательности. Стремление улуч­шить корреляционные свойства сигналов привело к созданию на основе М- последовательностей других последовательностей, сре­ди которых особое место занимают последовательности Голда, Кассами и некоторые другие.

Схема генератора, формирующего M-последовательность, в са­мом общем виде изображена на рис. 12.12. Основой генератора яв­ляется регистр сдвига, выполненный на триггерах (Т). Выходы неко­торых каскадов регистра через сумматоры по модулю 2 подключены к входу первого каскада. Двоичная последовательность

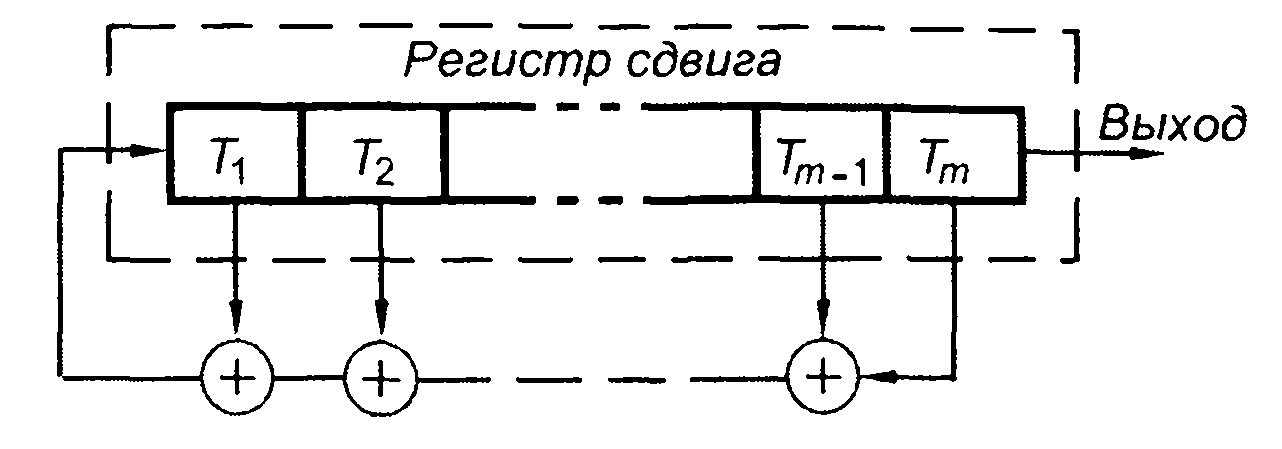
Рис. 12.12

на выходе генератора зависит от числа каскадов регистра, их начального состояния и вида обратной связи.

Формируемая двоичная последовательность является периоди­ческой, подчиняется принципу суперпозиции. Вследствие этого та­кая последовательность может рассматриваться как линейная, а генератор называется линейным. Максимальное число символов последовательности за один период составляет