ДЕТЕРМИНИРОВАННЫЕ СИГНАЛЫ 13 страница

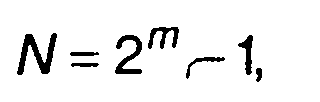(12.76)

где т - число каскадов.

Зависимость N от числа каскадов генератора т приведена в табл. 12.2 (m≤13). Число N определяет период кодовой после­довательности

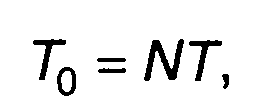(12.77)

где Т - длительность одного символа.

Таблица 12.2

Число М-последовательностей, формируемых т -каскадным генератором

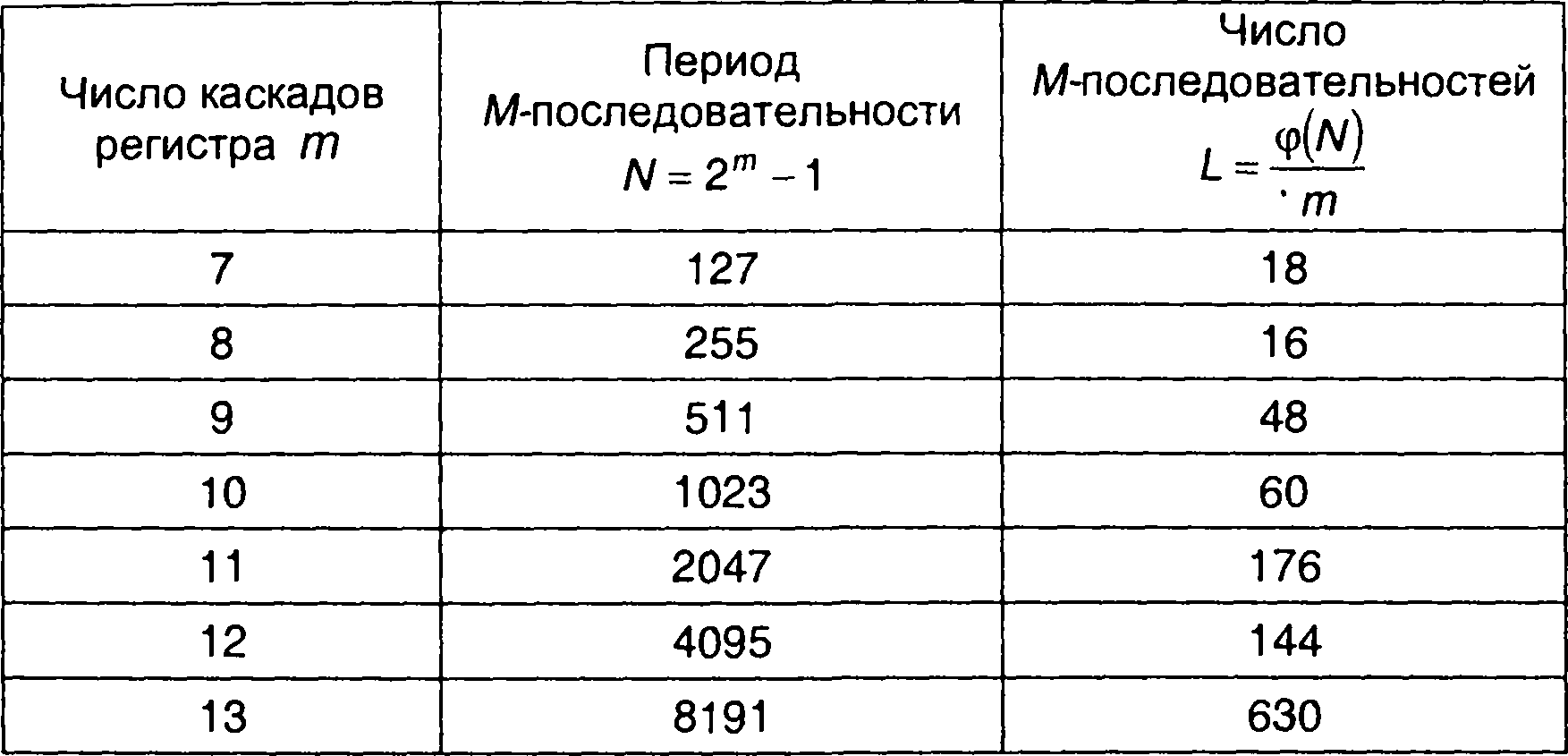
Последовательность, имеющая максимально возможный для выбранного способа генерирования период, называется макси­мальной или M-последовательностью. Последовательность, имеющая меньший период, называется не максимальной.

Генерируемую двоичную последовательность можно получить, если записать уравнения каждого из триггеров регистра. Символ на входе первого триггера в п-ом такте определяется уравнением

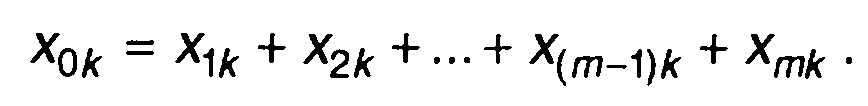(12.78)

В уравнении (12.78) х_1k представляет символ на выходе 1-го триггера в к-ом такте. Учитываются только те триггеры, которые входят в состав обратной связи. Символ х_0к в следующем k+1-м такте переходит на вход триггера T₁

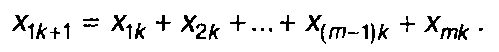(12.79)

На входе остальных триггеров регистра в k + 1 такте будут сим­волы

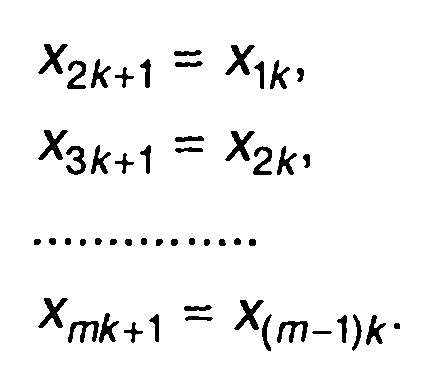(12.80)

В качестве примера приведем шестикаскадный генератор (рис. 12.13). Он формирует следующую двоичную M-последовательность:

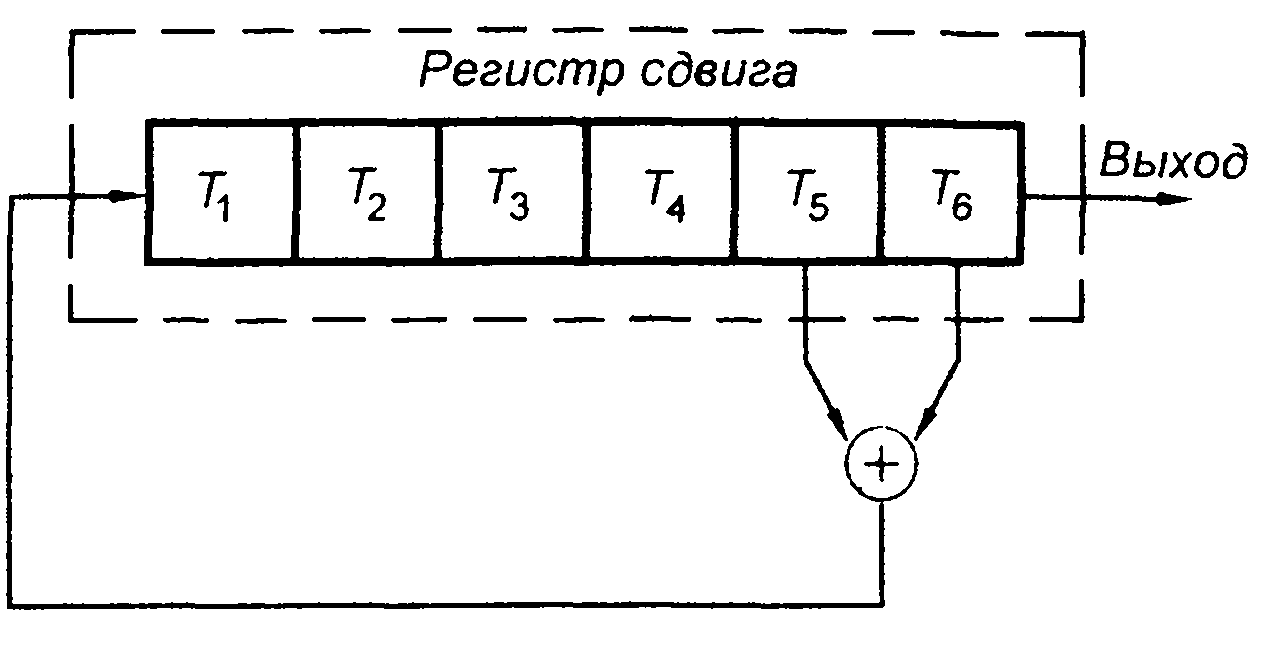
Рис. 12.13

Число M-последовательностей, формируемых m-каскадным ге­нератором, определяется выражением

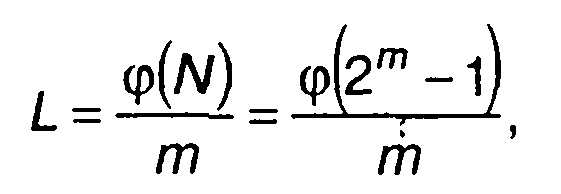(12.81)

где φ(х) - функция Эйлера.

Если число N раскладывается на простые множители, то φ(N) можем представить в виде

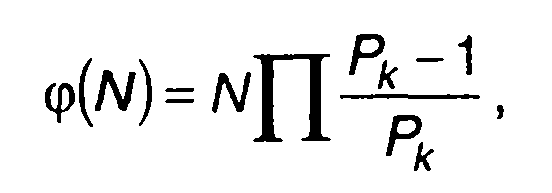(12.82)

где Р_к - простой множитель N.

Если N простое число, то

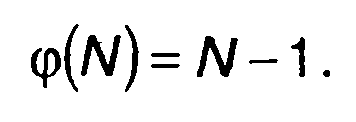(12.83)

M-последовательности довольно подробно исследованы, со­ставлены таблицы, позволяющие для заданного периода опреде­лить структуру генератора.

Спектры и корреляционные функции M-последовательностей могут быть получены с использованием вышеприведенных выра­жений.

Схема линейного генератора M-последовательностей не допус­кает одновременного появления нулей во всех каскадах, включен­ных в обратную связь. При установлении нулей в этих каскадах

сигнал на входе первого каскада отсутствует, происходит срыв в работе генератора. Указанного ограничения лишены генератора, формирующие нелинейные последовательности (для которых не выполняется принцип суперпозиции).

Генерирование нелинейных последовательностей может произ­водиться различными устройствами, в том числе с помощью гене­ратора на основе регистра сдвига с нелинейными операциями.

Анализ нелинейных генераторов затруднен вследствие большого их разнообразия и математических трудностей, возникающих вслед­ствие нелинейного характера описывающих их уравнений. При опи­сании спектральных и корреляционных характеристик нелинейных двоичных последовательностей, могут быть использованы соотно­шения, приведенные выше для кодовых сигналов.

12.4. Частотно-кодированные сигналы

Частотно-кодированный сигнал представляет последователь­ность радиоимпульсов, которые отличаются друг от друга только значениями несущей частоты. Закон изменения частоты определя­ется модулирующей кодовой последовательностью.

Частотно-кодированный сигнал описывается выражением

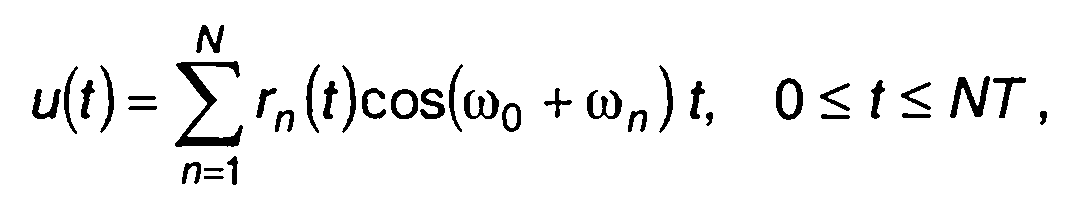(12.84)

или в комплексной форме (12.2). Комплексная огибающая ЧК сиг­нала

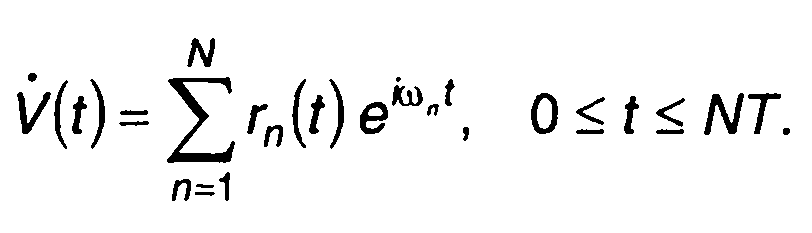(12.85)

Изменяющаяся частота ω_n может быть представлена в виде

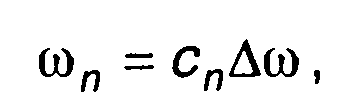(12.86)

где {с_п} - модулирующая кодовая последовательность (частотный код); ∆ω - шаг квантования по частоте.

На рис. 12.14 приведен пример бинарной кодовой последова­тельности {с_п} и соответствующий ЧК сигнал.

Спектральная плотность комплексной огибающей ЧК сигнала определяется (12.6). С учетом (12.85) выражение для спектральной плотности запишется в виде

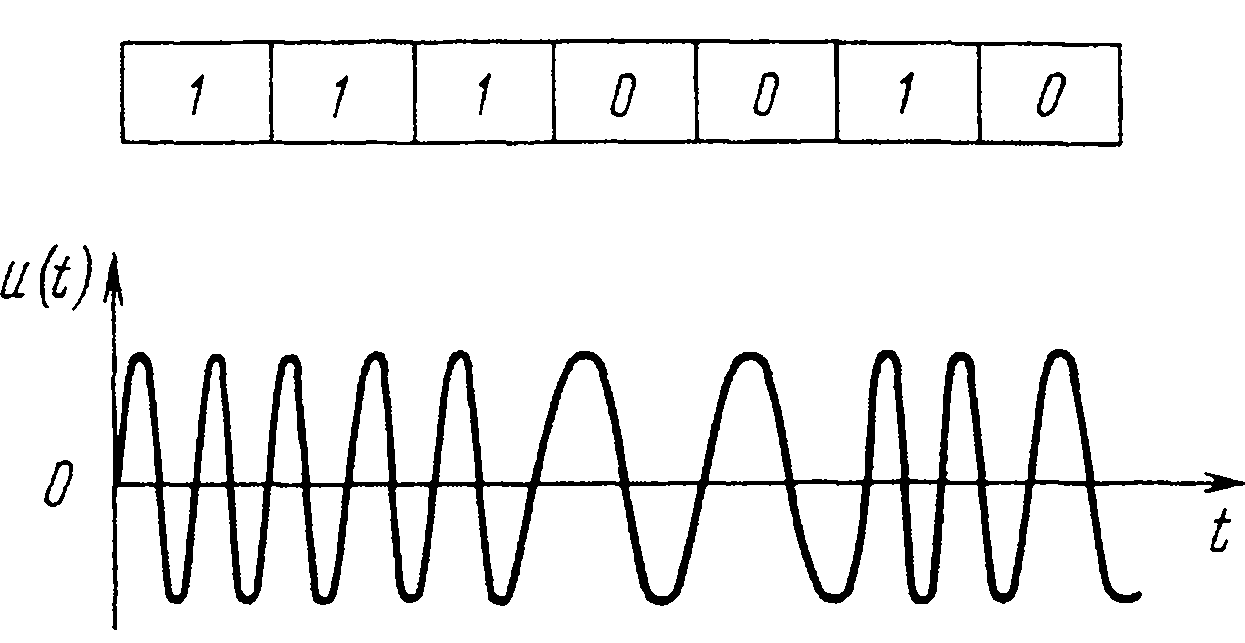
Рис. 12.14

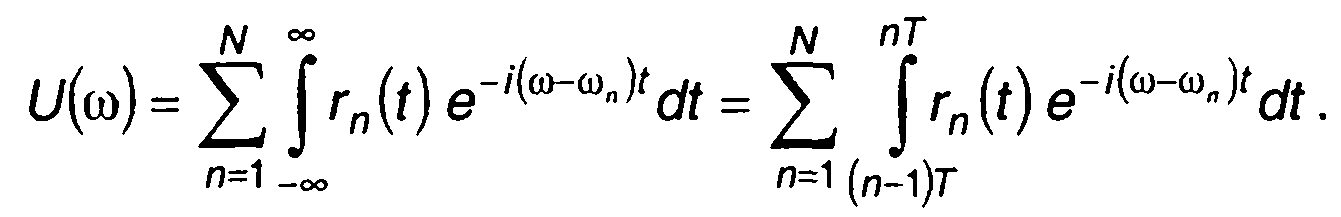(12.87)

Спектральная плотность сигнала определяется как сумма спек­тральных плотностей радиоимпульсов кодированного сигнала, от­личающихся несущей частотой и положением на временной оси. Спектральную плотность комплексной огибающей ЧК сигнала пред­ставим в виде

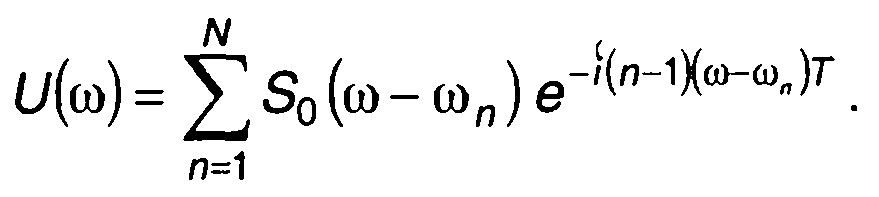(12.88)

При прямоугольной огибающей радиоимпульса спектральная плотность первого импульса определяется выражением

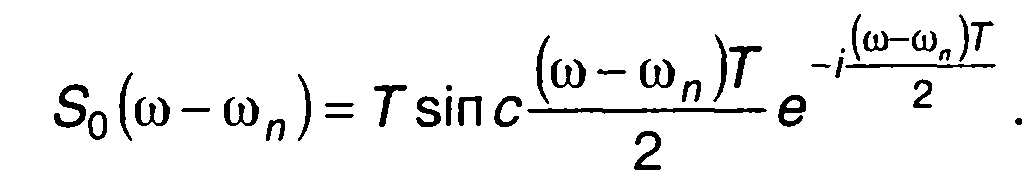(12.89)

Из (12.88) определим амплитудный спектр

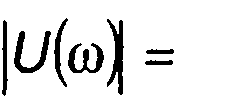(12.90)

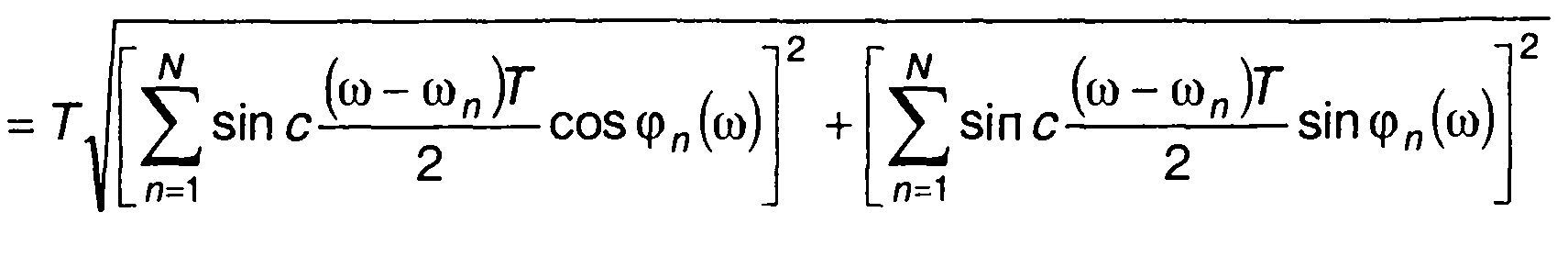
и фазовый спектр комплексной огибающей ЧК сигнала

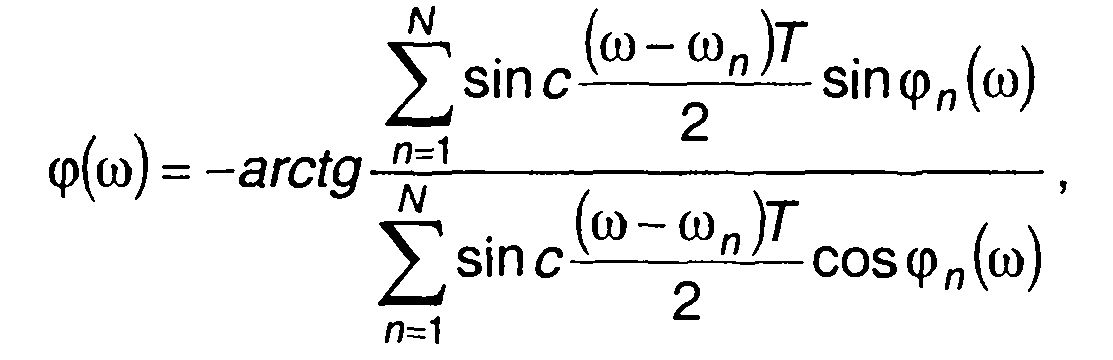(12.91)

где

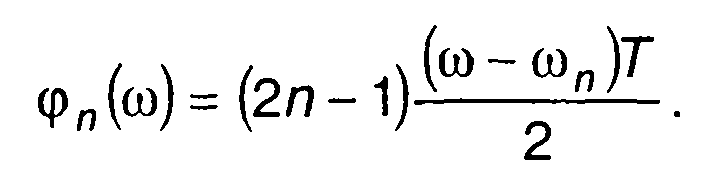
График амплитудного спектра комплексной огибающей ЧК сигнала (кодовая последовательность рис. 12.14) приведен на рис. 12.15.

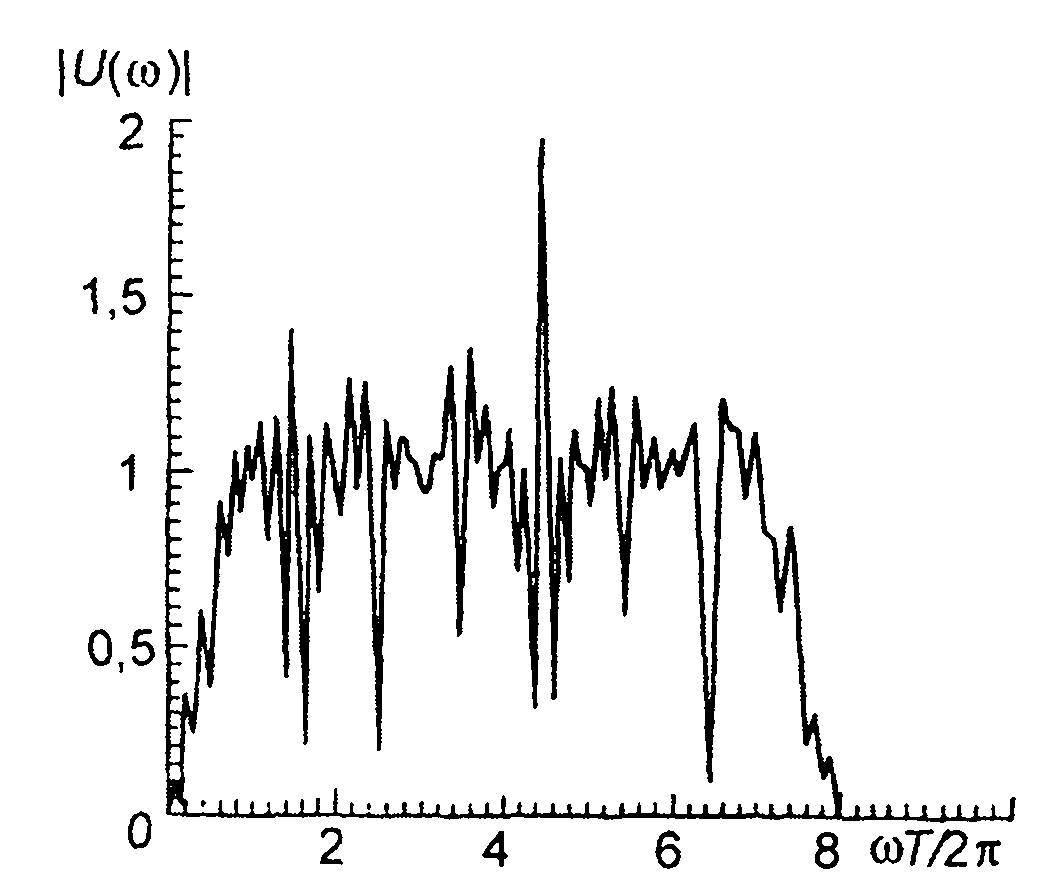
Рис. 12.15

Спектр симметричен относительно ω = 0. Как показывают при­веденные выражения, спектр ЧК сигнала определяется кодовой последовательностью {с_n} и шагом квантования.

Минимальный шаг квантования выбирается как

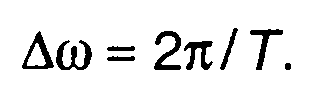(12.92)

При выборе шага квантования и бинарной модуляции база ЧК сигнала равна

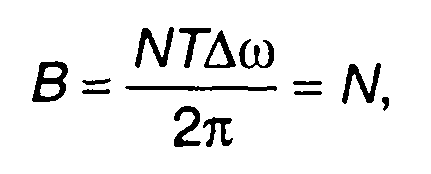(12.93)

т.е. определяется длиной кодовой последовательности.

Раздел 13.

АНАЛИЗ СИГНАЛОВ В ЛИНЕЙНЫХ ЦЕПЯХ

Методы анализа сигналов основаны на использовании различных преобразований, рассмотренных выше. Однако некоторые преобра­зования, такие, как преобразование Лапласа, z-преобразование, ис­пользуются в основном при анализе сигналов в линейных цепях (цифровых фильтрах).

Вследствие этого целесообразно рассмотреть сигналы в ли­нейных аналоговых цепях и цифровых фильтрах. Без такого рас­смотрения изложение методов анализа сигналов с использовани­ем преобразований Лапласа и z-преобразования носило бы фор­мальный характер.

В разделе рассматривается прохождение сигналов через анало­говые линейные цепи и цифровые фильтры только как иллюстра­ция методов анализа сигналов, и не затрагиваются задачи, связан­ные с анализом и синтезом самих цепей.

13.1. Прохождение сигнала через линейную цепь

Одной из основных характеристик линейной цепи является им­пульсная характеристика h(t). Она определяется как отклик линей­ной цепи на воздействие сигнала в виде импульсной функции. Представив сигнал на входе цепи s₁(t) в виде последовательности импульсных функций (с соответствующими коэффициентами) и используя принцип суперпозиции, для сигнала на выходе цепи по­лучим:

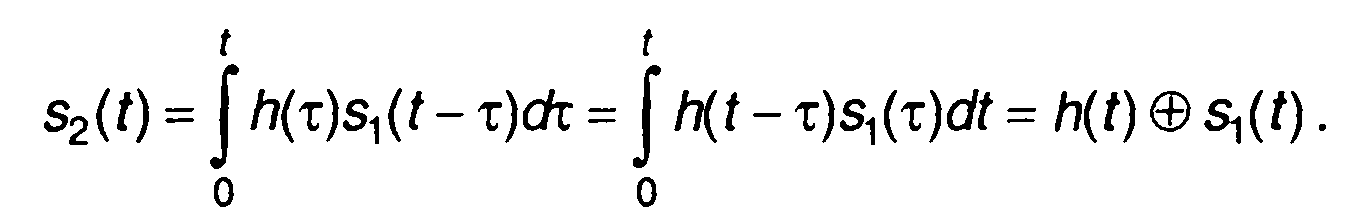(13.1)

Интеграл (13.1) представляет свертку импульсной характери­стики и сигнала на входе цепи. Знак 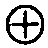в (13.1) и означает свертку h(t) и s₁(t). Интеграл свертки иногда называют также интегралом Дюамеля. Выражение (13.1) позволяет проводить анализ прохож­дения сигнала через линейную цепь при известной импульсной ха­рактеристике цепи.

В качестве примеров рассмотрим прохождение экспоненциаль­ного и прямоугольного импульсов через ЯС-цепь. Импульсная ха­рактеристика цепи имеет вид

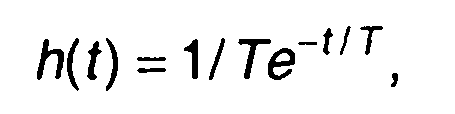
где Т- постоянная времени цепи.

1. При подаче на вход цепи экспоненциального импульса (рис. 13.1,а)

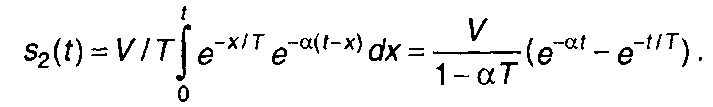
сигнал на выходе цепи определяется выражением (рис. 13.1,б)

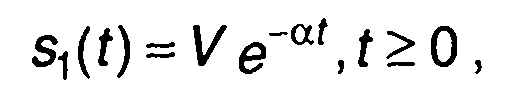
2. При подаче на вход цепи сигнала в виде прямоугольного им­пульса (рис. 13.2,а)

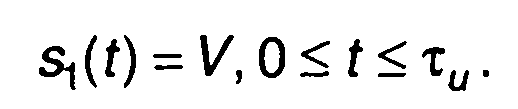
Сигнал на выходе цепи (рис. 13.2,6): при 0 < t < τ_и:

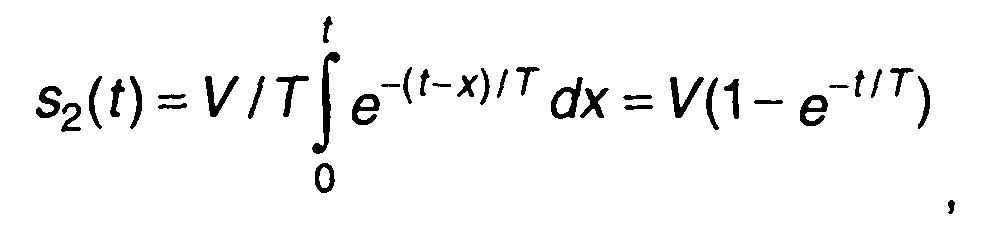
при t ≥ τ_u:

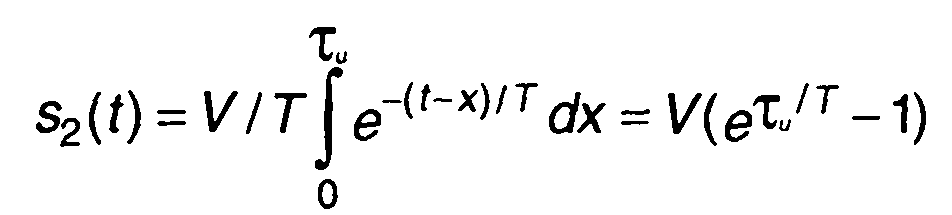
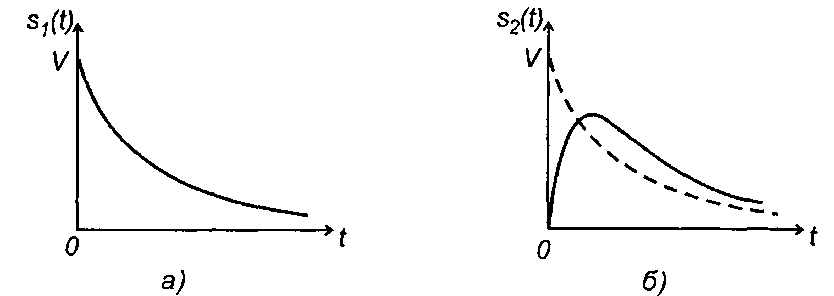
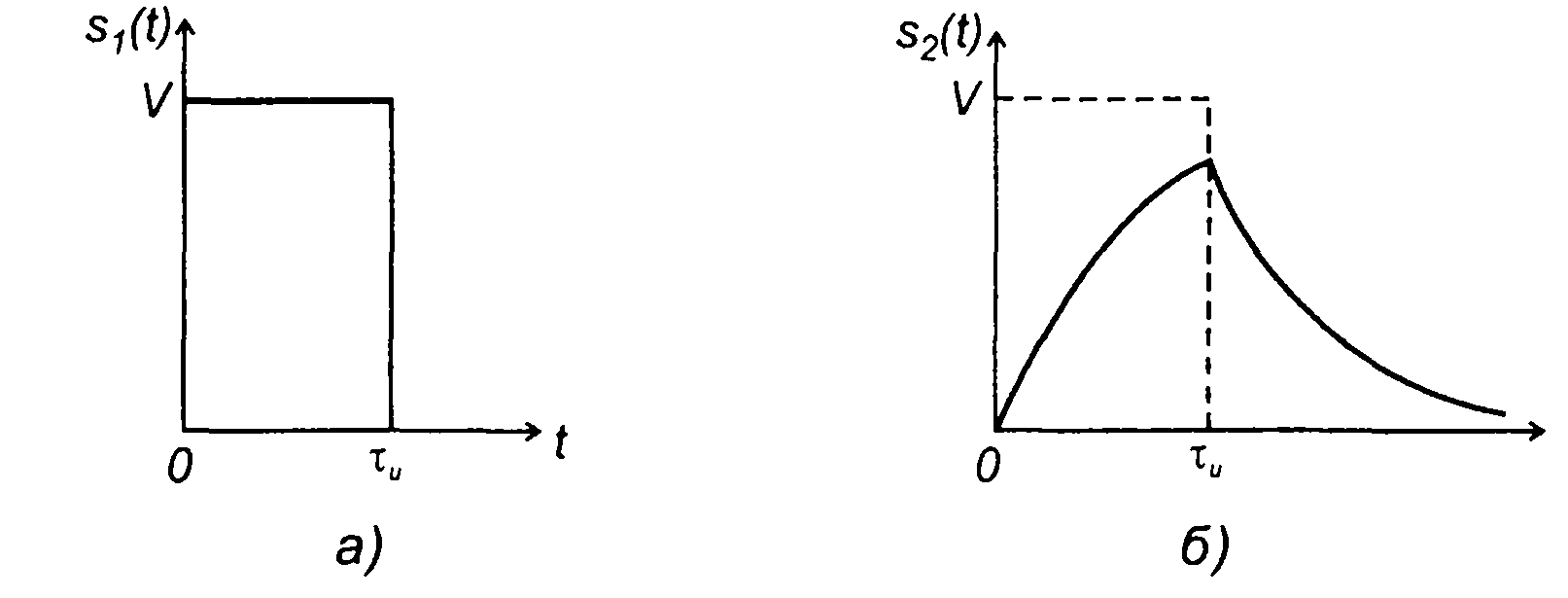
Рис. 13.2

В частотной области линейная цепь описывается комплексной частотной характеристикой. Комплексная частотная характеристи­ка (частотная характеристика) определяется преобразованием Фу­рье импульсной характеристики

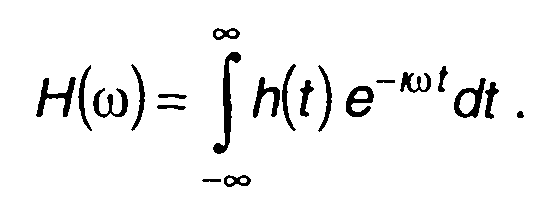(13.2)

Обратное преобразование Фурье позволяет перейти от Н(ω) к h(t):

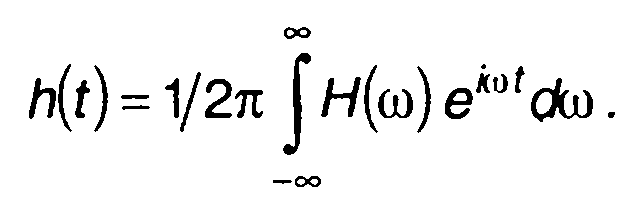(13.3)

Учитывая, что h(t) = 0 при t < 0 , условие существования преоб­разования Фурье импульсной характеристики записывается в виде

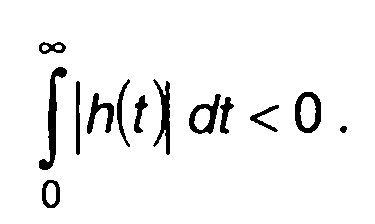(13.4)

Записанное условие является условием устойчивости линейной цепи.

В общем случае частотная характеристика является комплекс­ной величиной и ее можно представить в виде

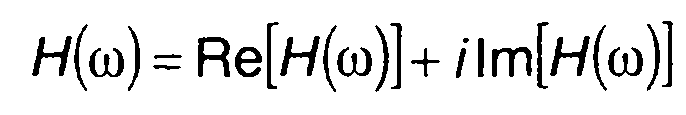(13.5)

или

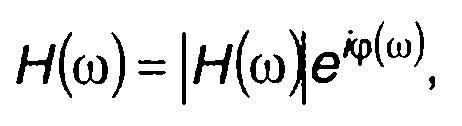(13.6)

где

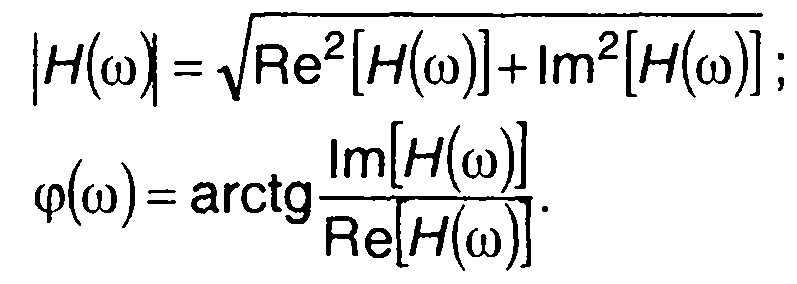
Модуль |Н(ω)| представляет амплитудно-частотную характери­стику, аргумент φ(ω) - фазо-частотную характеристику цепи.

Частотная характеристика позволяет проводить анализ прохож­дения сигнала через цепь, используя спектральную плотность сиг­нала. Преобразование Фурье левой и правой частей (13.1) дает (свойство преобразования Фурье)

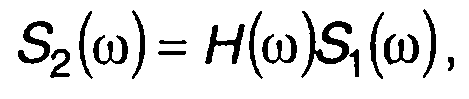(13.7)

где S₁(ω) и S₂(ω) - спектральные плотности сигналов на входе и выходе цепи.

OtS₂(ω) можно перейти к сигналу на выходе цепи

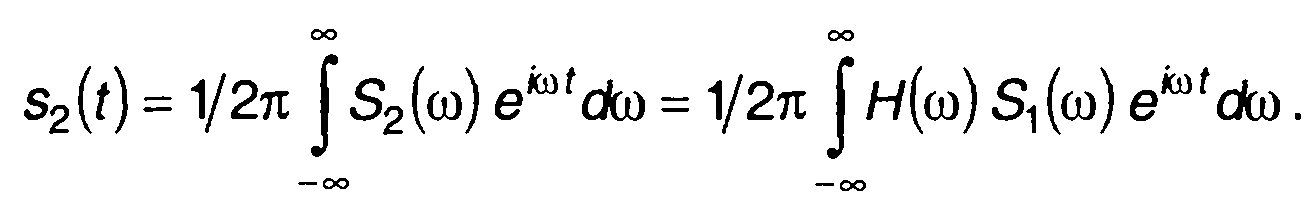(13.8)

Таким образом, имея частотную характеристику, можно прово­дить анализ цепи в частотной области. Простота выражения (13.7) обуславливает простоту спектрального метода анализа.

Примеры.

1. Прохождение экспоненциального импульса через RС-цепь. Сигналу на входе цепи

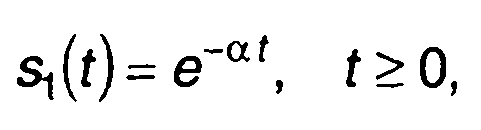
соответствует спектральная плотность

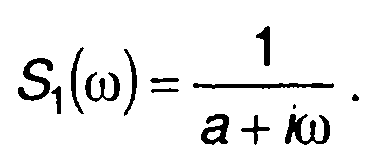
Частотная характеристика RС-цепи имеет вид

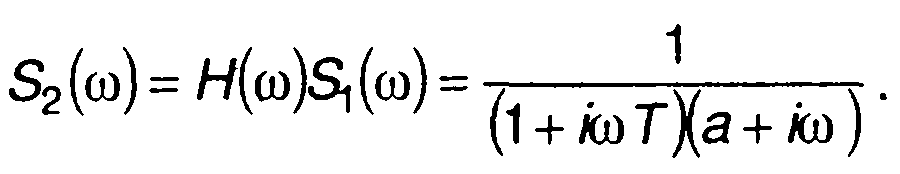
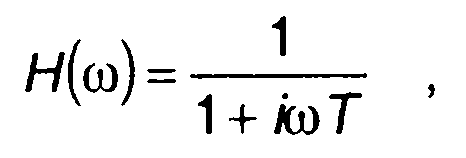
где Т = RC- постоянная времени цепи.

Спектральная плотность на выходе цепи описывается выраже­нием

Сигнал на выходе цепи определяется обратным преобразова­нием Фурье S₂(ω)

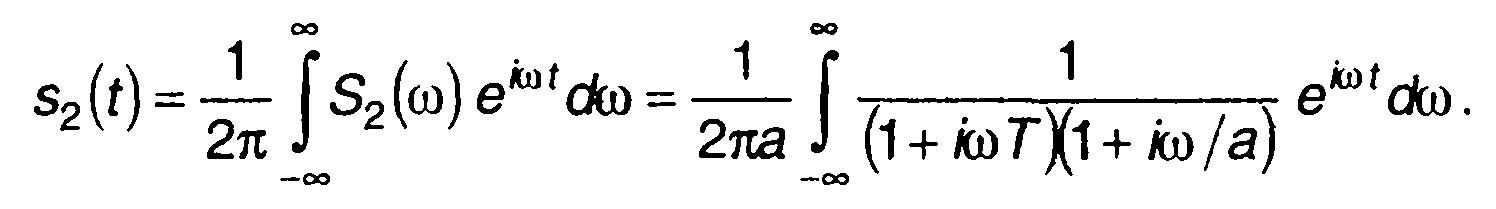
Для вычисления интеграла разложим подынтегральную функ­цию на элементарные дроби

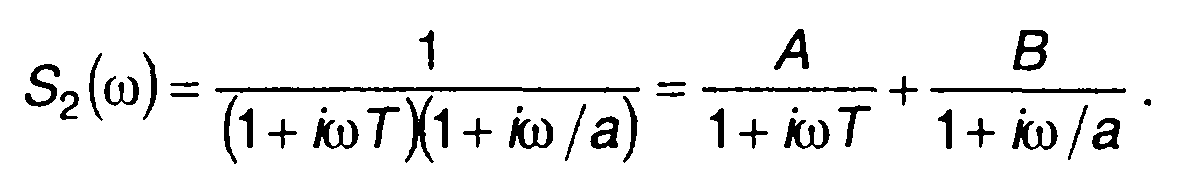
Из записанного равенства получим

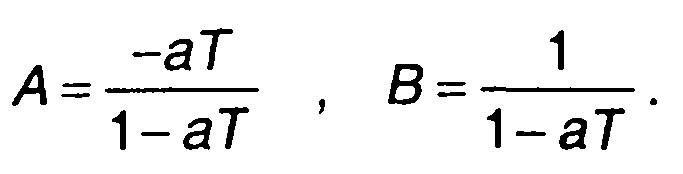
С учетом выполненного разложения найдем

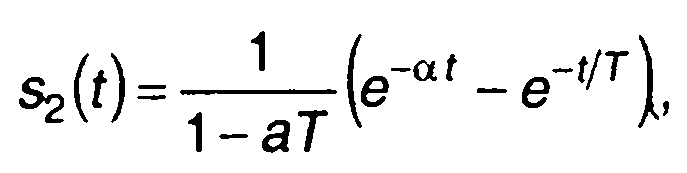
что совпадает с ранее полученным результатом.

Практика анализа прохождения сигналов через линейные цепи показывает, что спектральный метод анализа особенно удобен в том случае, когда при описании сигнала можно ограничиться его спектром.

Выражение для спектральной плотности энергии сигнала на вы­ходе линейной цепи можно получить с учетом (13.7) в виде:

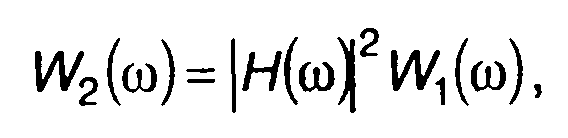(13.9)

где W₁(ω) = |S₁(ω)(² и W₂(ω) = |S₂(ω)|² - спектральные плотности энергии сигналов на входе и выходе цепи.

Преобразование Фурье спектральной плотности энергии W(ω) представляет автокорреляционную функцию сигнала

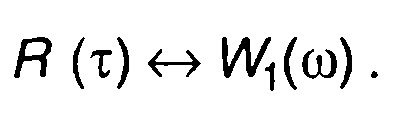(13.10)

Величине |Н(ω)|² соответствует по Фурье функция

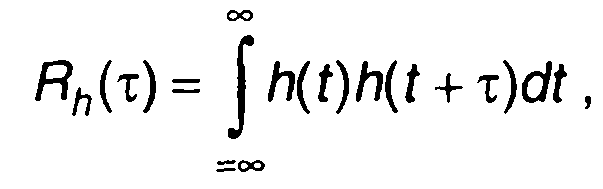(13.11)

которая может рассматриваться как автокорреляционная функция импульсной характеристики цепи. Таким образом,

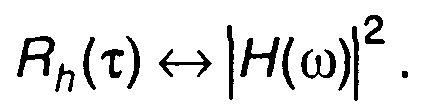(13.12)

С учетом (13.11) и (13.12), переходя к временной области, из

(13.9) получим

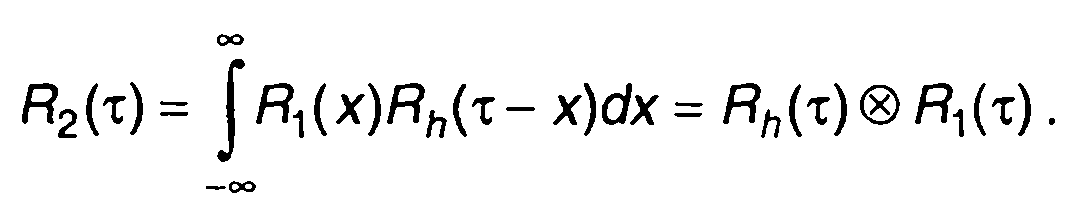(13.13)

Выражение для взаимной корреляционной функции сигналов на выходе и входе цепи записывается в виде

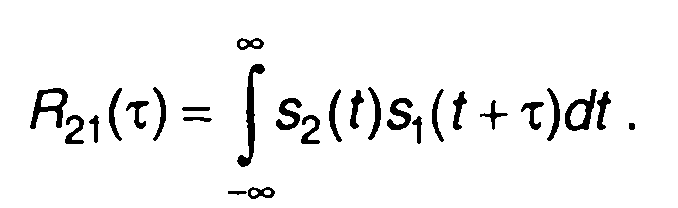(13.14)

Преобразование Фурье левой и правой частей (13.14) дает

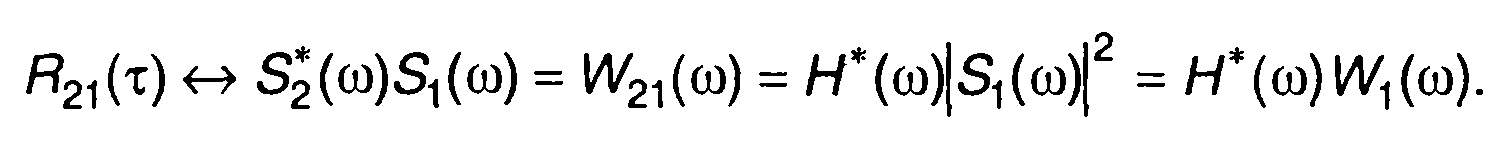(13.15)

Переходя к временной области, получим

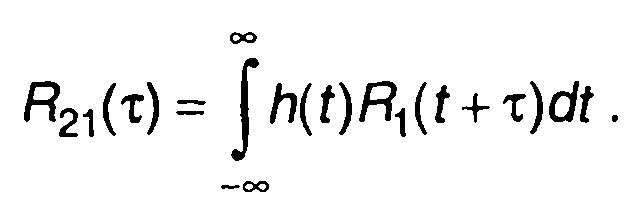(13.16)

В записанных соотношениях важно соблюдать требуемую по­следовательность функций. При изменении последовательности имеем

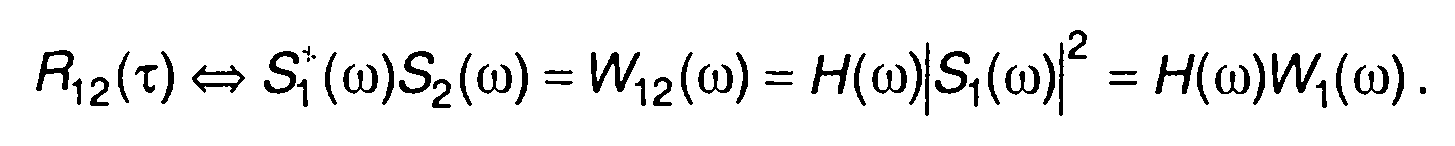(13.17)

Таким образом,

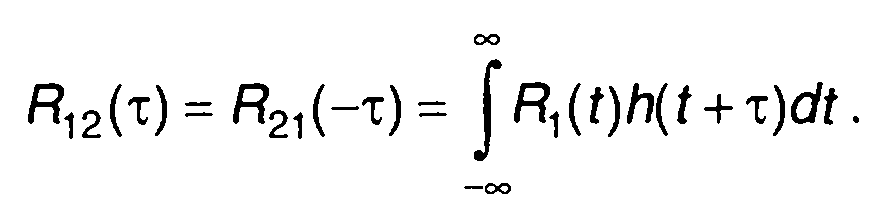(13.18)

Одной из основных характеристик линейной цепи является пе­редаточная функция. Она определяется аналогично частотной ха­рактеристике - как преобразование Лапласа импульсной характе­ристики цепи

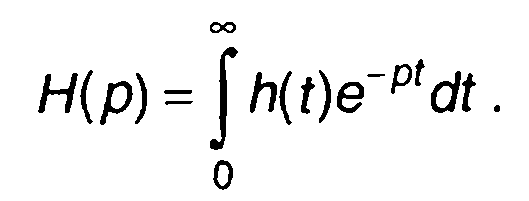(13.19)

Свертке во временной области, определяющей сигнал на выхо­де линейной цепи

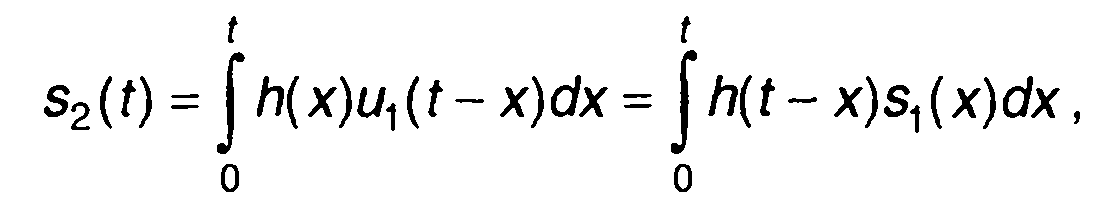(13.20)

соответствует произведение передаточной функции и изображения сигнала на входе (свойство преобразования Лапласа)

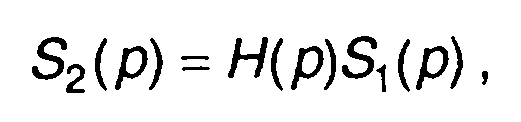(13.21)

где S₁(p), S₂(p) - преобразования Лапласа сигналов на входе и вы­ходе цепи.

Обратное преобразование Лапласа (13.21) позволяет опреде­лить сигнал на выходе цепи

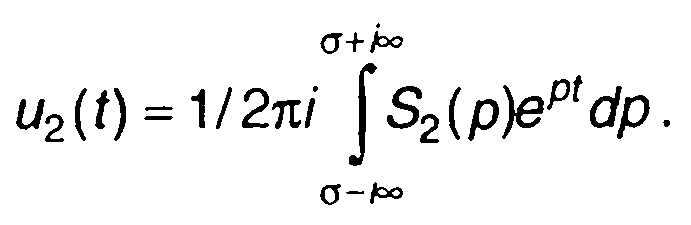(13.22)

Подходы к решению интеграла (13.22) описаны в разд. 4.

Метод анализа линейных цепей, основанный на использовании преобразования Лапласа, называется операторным методом. При­ведем примеры его применения.

1. Прохождение прямоугольного импульса через RС-цепь. Передаточная функция цепи

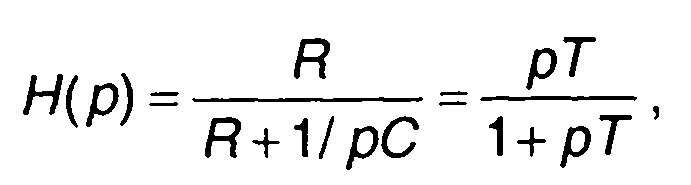
где Т = RC- постоянная времени цепи.

Чтобы определить h(t), разложим Н(р) на простые дроби: 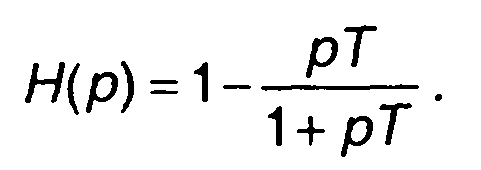Учитывая, что 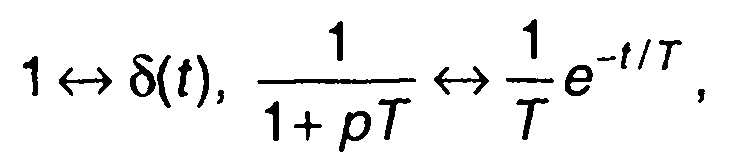получим

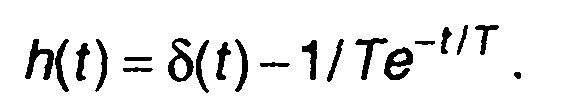
Изображение сигнала (прямоугольного импульса) на входе име­ет вид

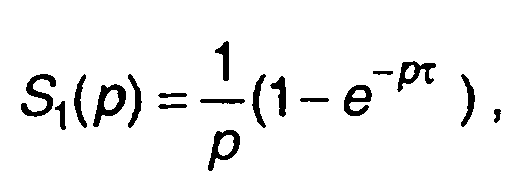
где τ-длительность импульса, сигнала на выходе:

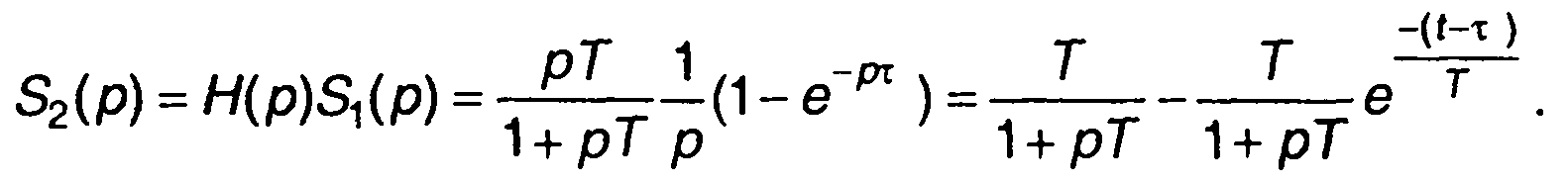
Полученному изображению соответствует оригинал

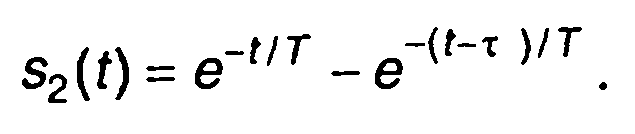
2. Прохождение прямоугольного импульса через LCR- цепь. Передаточная функция цепи

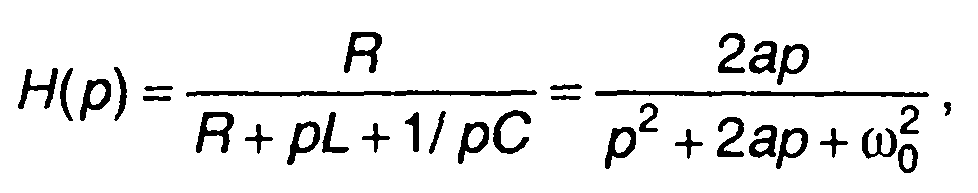
где ω₀² = 1/√(LC), a - RI2L, R, С, L - параметры цепи.

Соответствующая импульсная характеристика имеет вид

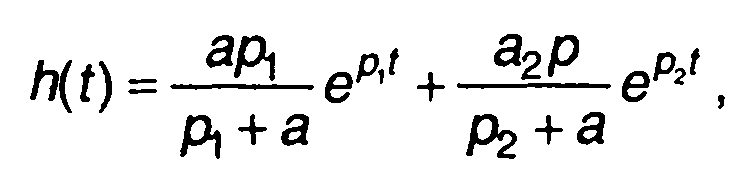
где р_к - корни знаменателя Н(р).

После преобразования получим

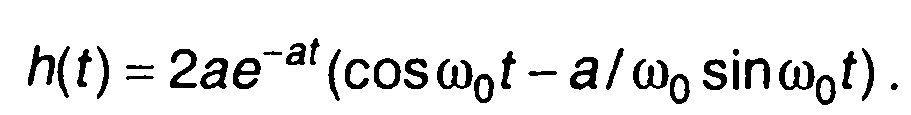
При достаточно большой добротности цепи (а<<ω₀), можно при­нять

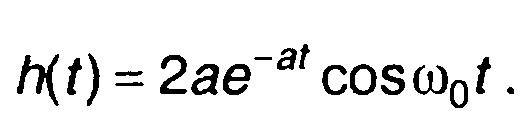
Изображение сигнала на выходе цепи с учетом изображения сигнала на входе (прямоугольный импульс, амплитуда равна еди­нице) получим в виде

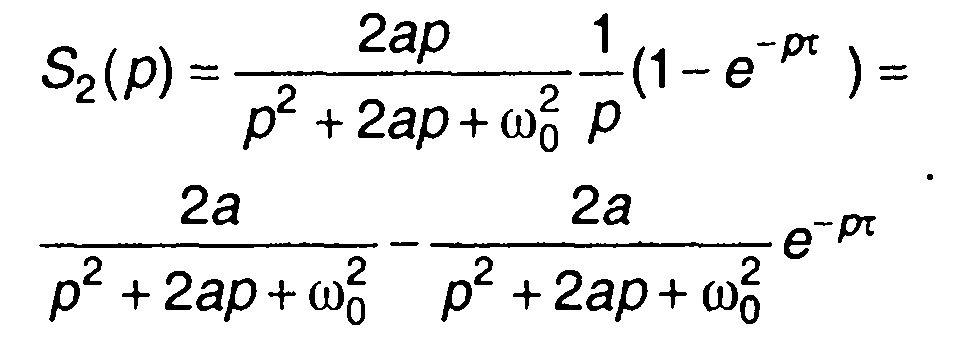
Оригинал, соответствующий первому слагаемому, определяет­ся как

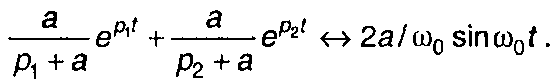
Оригинал, соответствующий второму слагаемому, отличается только смещением во времени на интервал т . Таким образом,

получим

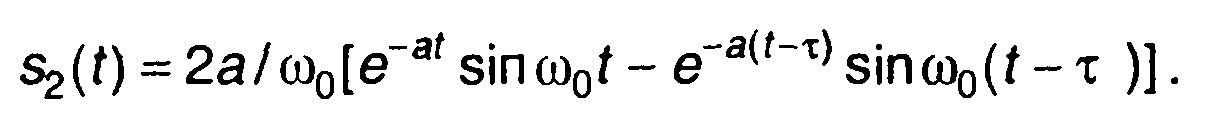
Одним из важных применений преобразования Лапласа являет­ся решение линейных дифференциальных уравнений с постоян­ными коэффициентами, описывающих прохождение сигналов че­рез линейные цепи

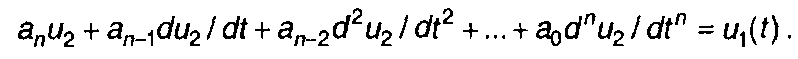(13.23)

Преобразование Лапласа левой и правой частей (13.23) приво­дит к следующему выражению

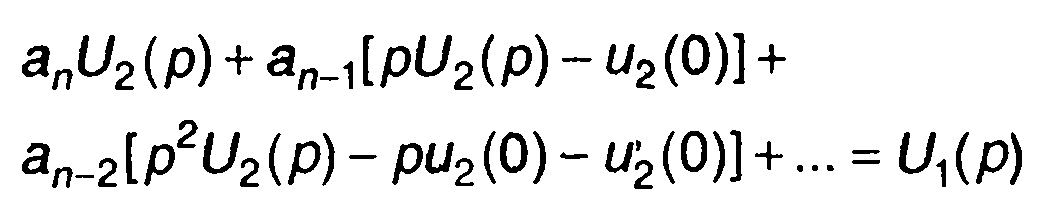(13.24)

Перепишем (13.24) в виде

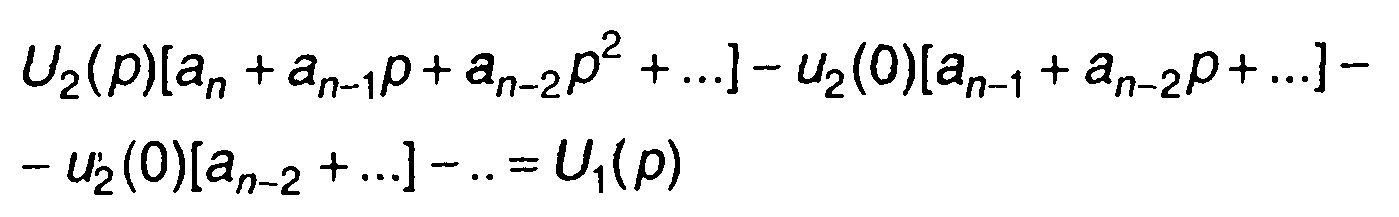(13.25)

Из (13.25) получим изображение сигнала на выходе цепи

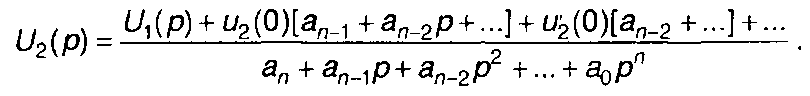(13.26)

Если все начальные значения равны нулю, то

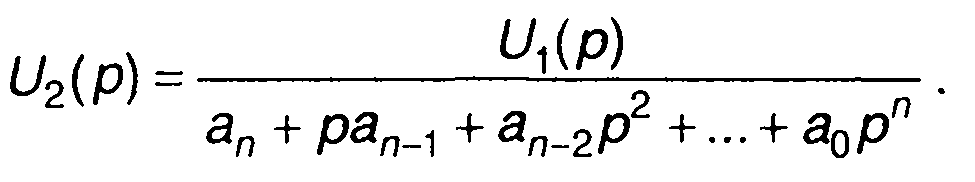(13.27)

По изображению (13.27) можно получить оригинал - сигнал на выходе цепи.

Рассмотрим пример использования преобразования Лапласа при решении дифференциального уравнения

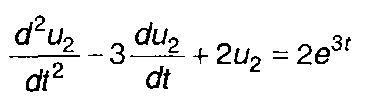
при нулевых начальных условиях.

Переходя к изображению левой и правой частей уравнения, за­пишем

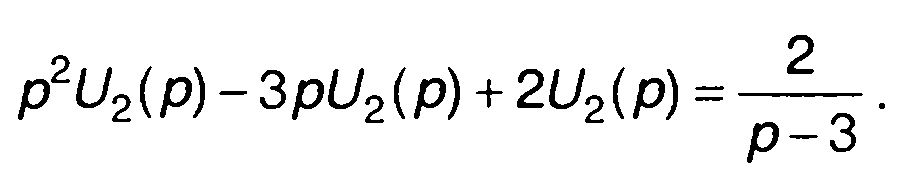
Для изображения сигнала на выходе имеем

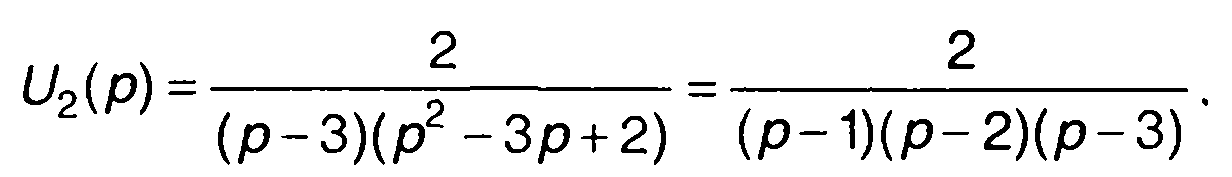
Переходя от изображения к оригиналу - сигналу на выходе, по­лучим

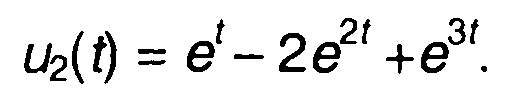
13.2. Прохождение сигнала через узкополосную цепь

13.2.1 Узкополосные цепи, их низкочастотные эквиваленты

Для передачи узкополосных сигналов, как правило, используются узкополосные цепи. Радиотехническая цепь называется узкополос­ной (избирательной), если ее частотная характеристика отлична от нуля в полосе частот, ширина которой значительно меньше средней частоты (рис. 13.3,а). Такие цепи находят применение в различных системах и их анализ занимает важное место в общем анализе сиг­налов, цепей и систем.

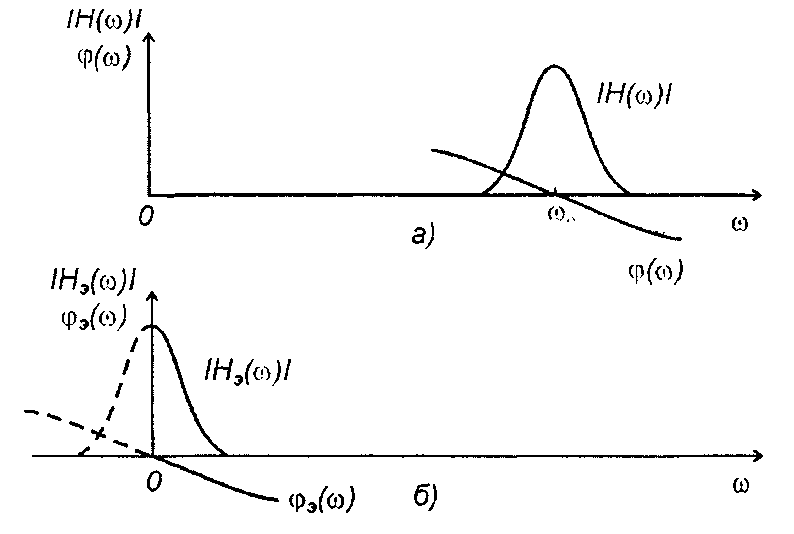
Рис. 13.3

В качестве основных характеристик линейной цепи выше рас­сматривались импульсная и частотная характеристики, связанные парой преобразований Фурье

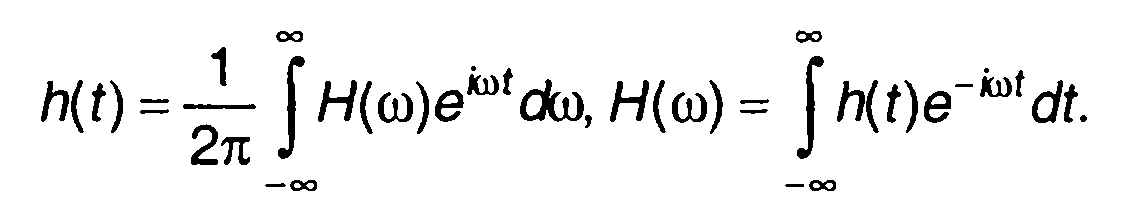(13.28)

При описании узкополосной цепи целесообразно ввести поня­тие низкочастотного эквивалента. Использование этого понятия позволяет упростить анализ узкополосных цепей.

Для определения низкочастотного эквивалента рассмотрим цепь, частотная характеристика которой получается смещением частотной характеристики узкополосной цепи Н(ω) в область низ­ких частот на значение средней частоты ω₀ (рис. 13.3,6). Тогда для области положительных частот можем записать

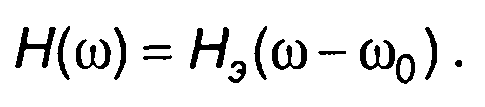(13.29)

Цепь с частотной характеристикой, полученной таким образом, представляет низкочастотный эквивалент цепи. Частотной харак­теристике низкочастотного эквивалента соответствует импульсная характеристика

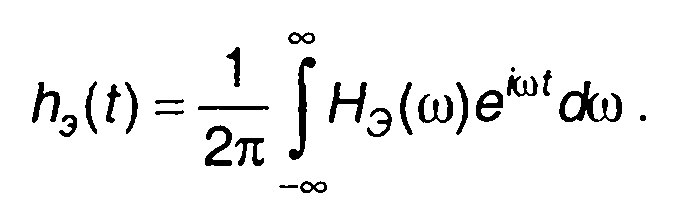(13.30)

Обычно частотная характеристика узкополосной цепи является симметричной относительно средней частоты Шо'.

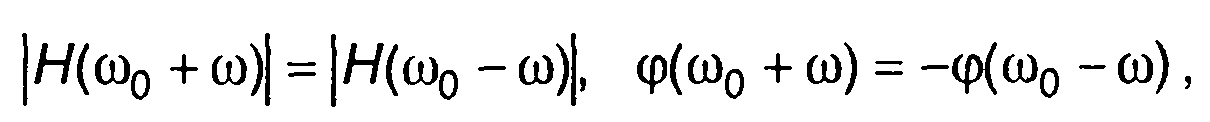(13.31)

где |Н(ω)|, φ(ω) - амплитудно-частотная и фазо-частотная характе­ристики цепи.

Для симметричной частотной характеристики с учетом того, что импульсная характеристика является действительной функцией времени, можно записать

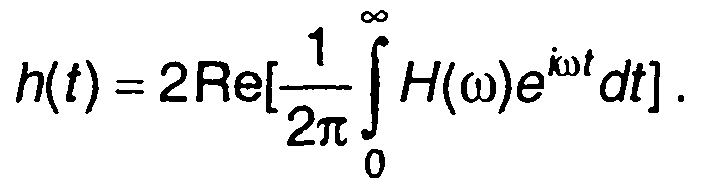(13.32)

Подставляя (13.29) в (13.32), получаем

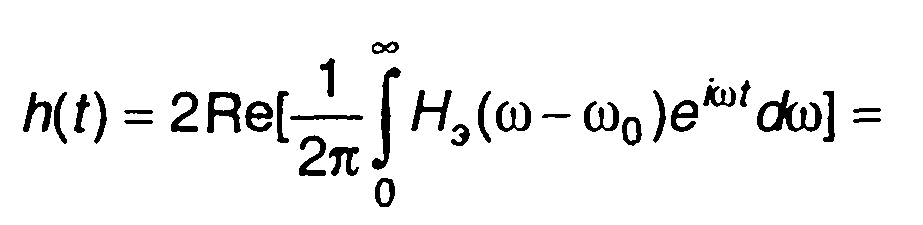(13.33)

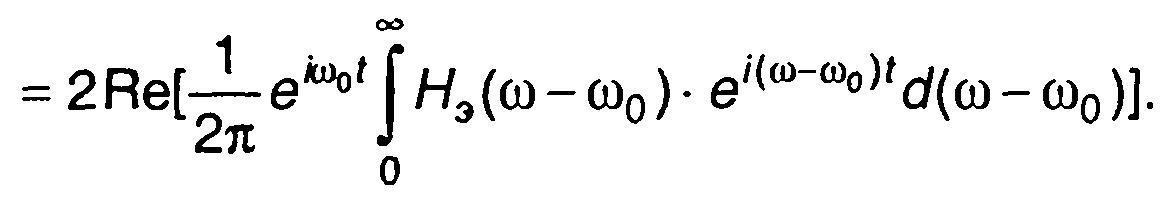
С учетом узкополосности цепи нижний предел в (13.33) можем заменить на -∞

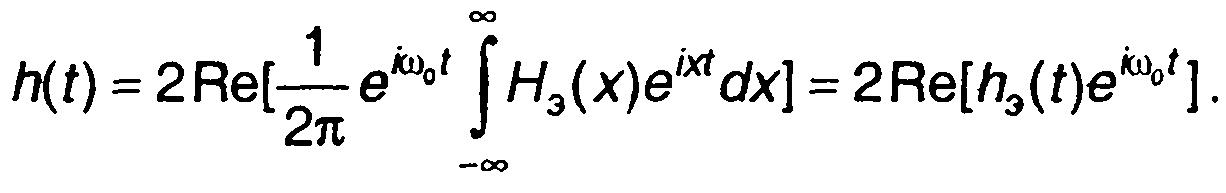(13.34)

Таким образом, записано соотношение между импульсными ха­рактеристиками узкополосной цепи и ее низкочастотного эквива­лента. Соотношение между частотными характеристиками узкопо­лосной цепи и низкочастотного эквивалента для всей оси частот получим из преобразования Фурье

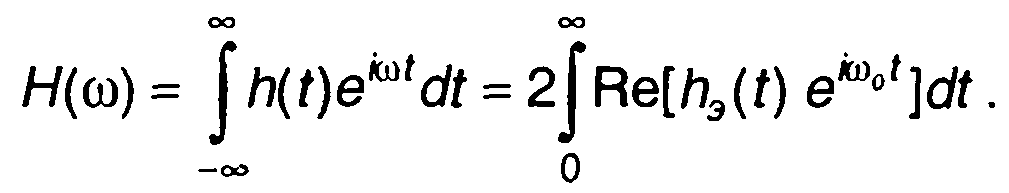(13.35)

Используя соотношение для комплексной величины

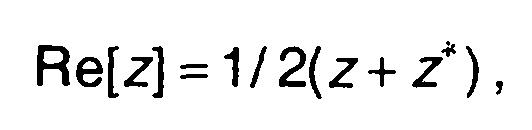(13.36)

где z*- комплексно сопряженная величина.

Из (13.35) получим

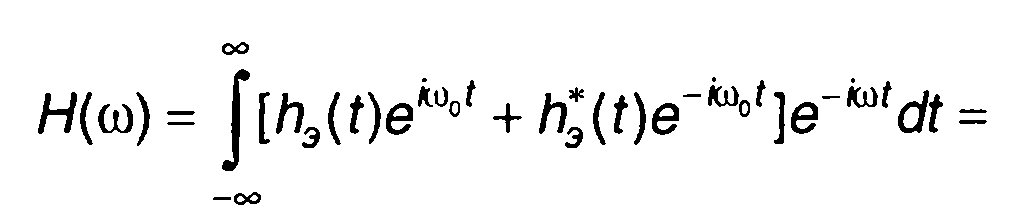(13.37)

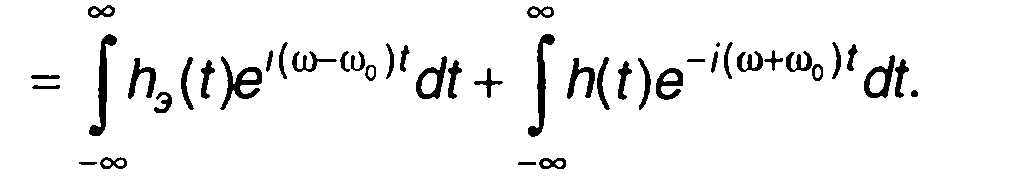
Таким образом,

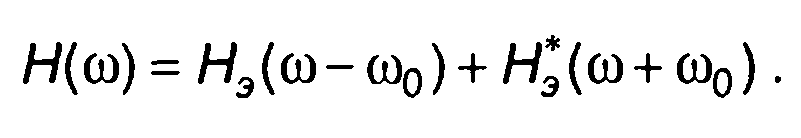(13.38)

Низкочастотный эквивалент узкополосной цепи является мате­матической моделью цепи, описываемой импульсной и частотной характеристиками. Его использование при анализе узкополосной цепи является приемом, который часто позволяет упростить про­водимый анализ. Соотношения (13.34) и (13.38) описывают пере­ход от характеристик низкочастотного эквивалента к характеристи­кам узкополосной цепи.

В качестве примера рассмотрим характеристики LRC - цепи (рис. 13.4,а). Частотная характеристика цепи имеет вид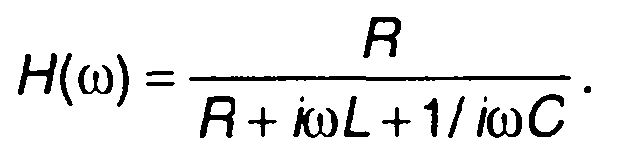

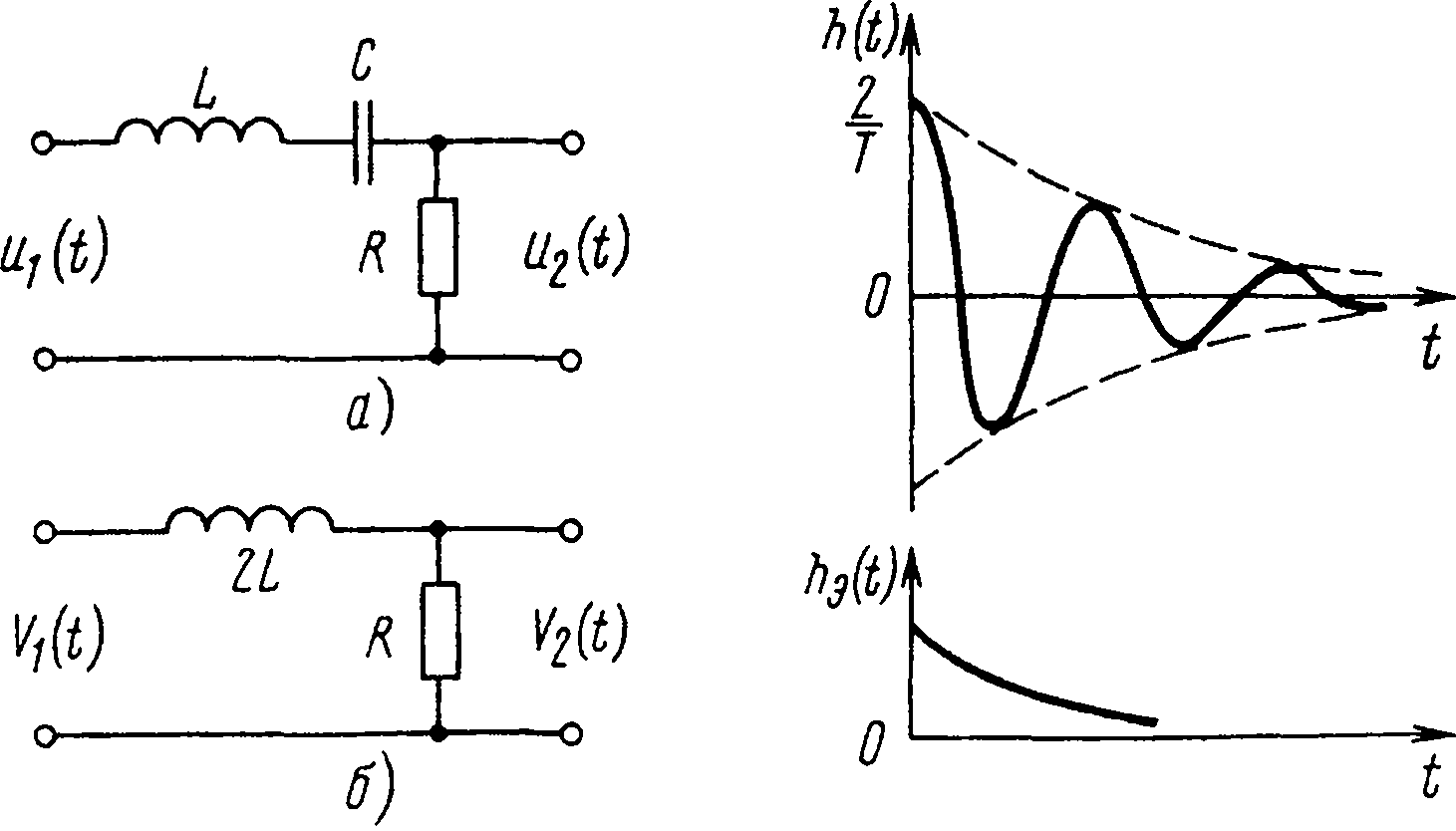
Рис.13.4

При выполнении условия узкополосности 1/√(LC) >> R/2L можно принять

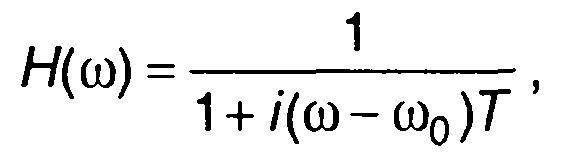
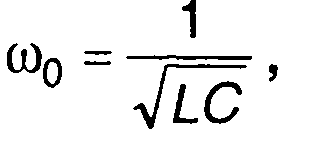
а выражение для Н(ω) преобразовать к виду где Т = 2L/R.

Переходя к эквивалентной низкочастотной цепи (рис. 13.4,б), получаем

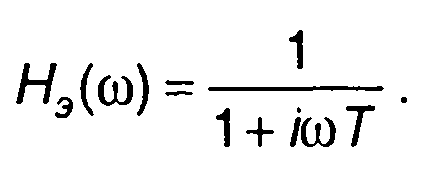
Импульсная характеристика эквивалентной низкочастотной це­пи имеет вид

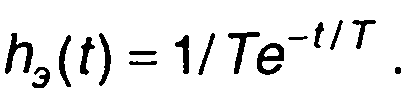
От h_э(t) можем перейти к импульсной характеристике узкополос­ной цепи (рис. 13.4,а)

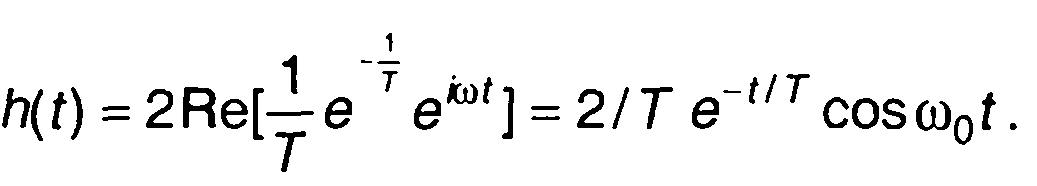
13.2.2 Прохождение узкополосного сигнала через узкополосную цепь

Анализ прохождения сигнала через узкополосную цепь наибо­лее удобно проводить с использованием комплексного представ­ления сигналов: на входе

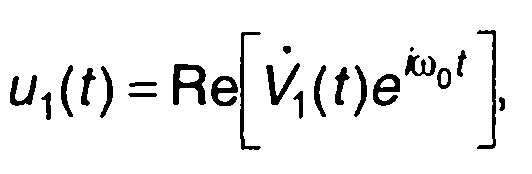(13.39)

на выходе

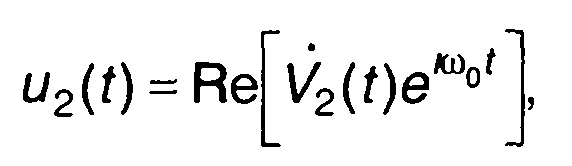(13.40)

где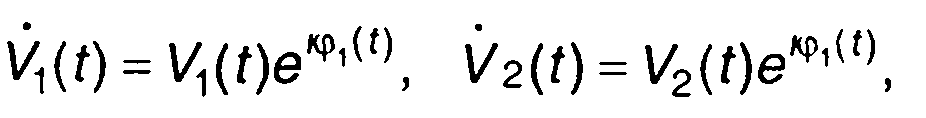

Спектральная плотность сигнала на выходе цепи S₂(ω) определяется выражением

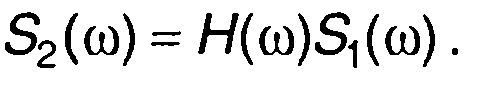(13.41)

Спектральная плотность сигнала на входе S₁(ω) определяется через спектральную плотность его комплексной огибающей U1(ω)

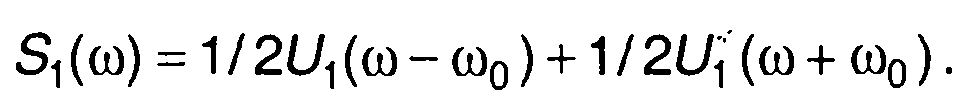(13.42)

Как правило, несущая частота сигнала совпадает со средней частотой полосы пропускания цепи. С учетом этого условия выра­жение для частотной характеристики цепи можем записать в виде

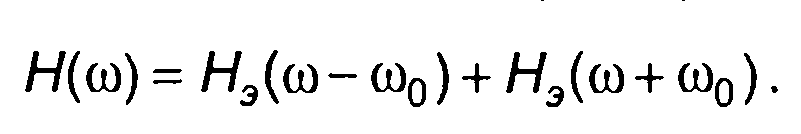(13.43)

Подставляя (13.43) и (13.42) в (13.41), получаем

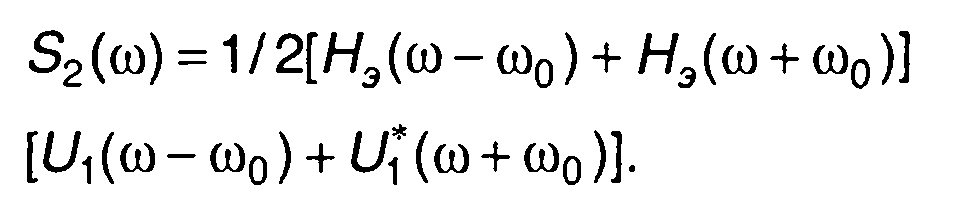(13.44)

Для узкополосного сигнала (13.44) перепишется в виде

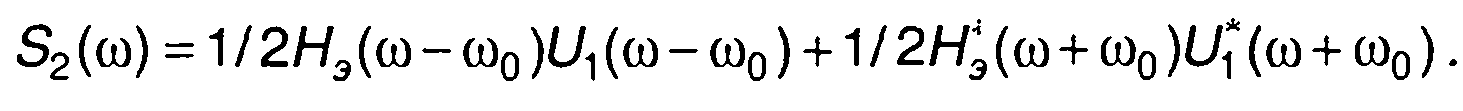(13.45)

Учитывая соотношение между спектральной плотностью сигна­ла и спектральной плотностью комплексной огибающей

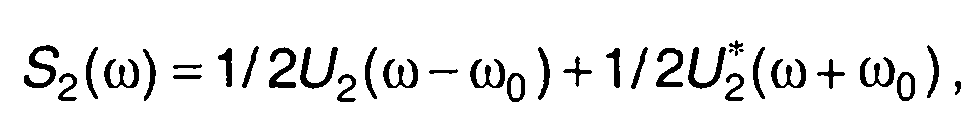(13.46)

можем определить спектральную плотность огибающей сигнала на выходе цепи как

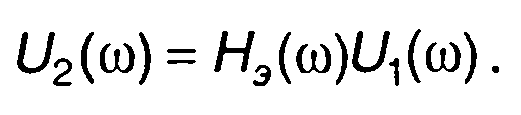(13.47)

Соотношения, аналогичные (13.45), можно получить для спек­тральной плотности энергии W₂(ω) на выходе узкополосной цепи