ДЕТЕРМИНИРОВАННЫЕ СИГНАЛЫ 16 страница

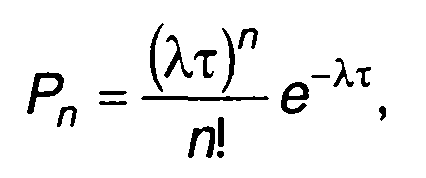(15.48)

где Р_п - вероятность n перемен знака на интервале времени τ; λτ = μ - среднее число переменных знака.

Вероятность числа перемен знака на рассматриваемом интер­вале времени не более п определяется как

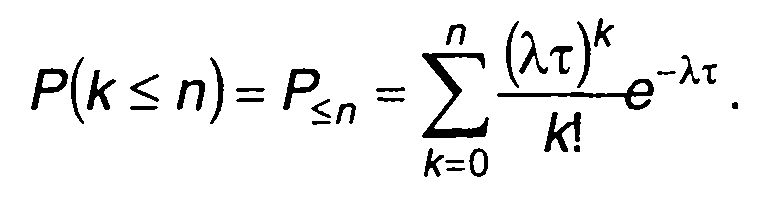(15.49)

С увеличением значения μ = λт распределение Пуассона при­ближается к нормальному со средним и дисперсией, равны­ми μ.Это означает, что для больших значений μ можем записать следующее выражение:

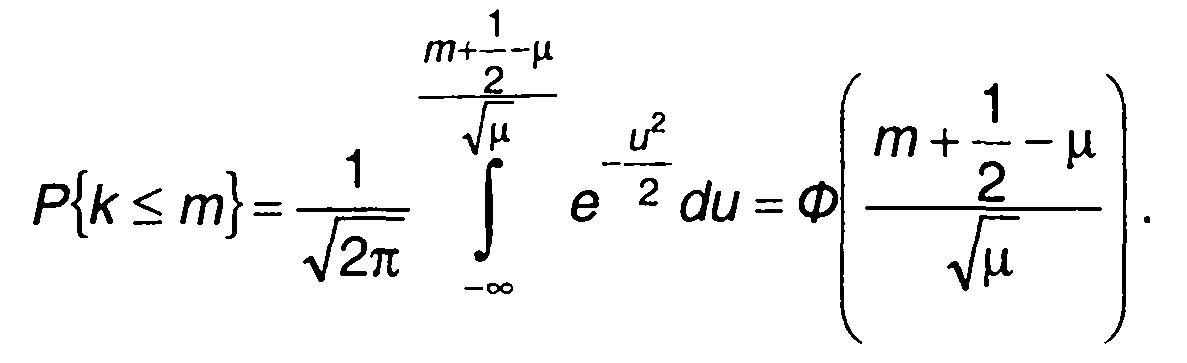(15.50)

Поправка 1/2 в (15.50) не является обязательной, но она улуч­шает аппроксимацию нормальным законом при сравнительно не­больших значениях μ.

Для телеграфного случайного сигнала р = 0,5

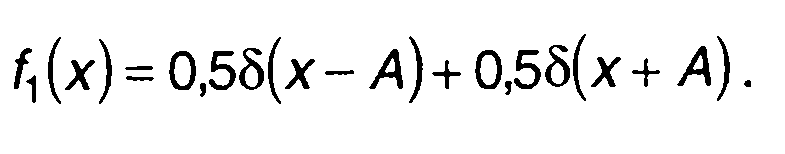(15.51)

Моменты распределения вероятностей т_п = 0.

Вероятность того, что на интервале т не будет перемены знака (отсутствует пересечение случайным процессом нулевого уровня) найдется из (15.48)

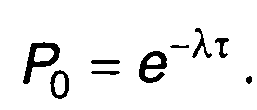(15.52)

Значение Р₀ определяет вероятность того, что интервал между пересечениями случайным процессом нулевого уровня будет не меньше т. Величина

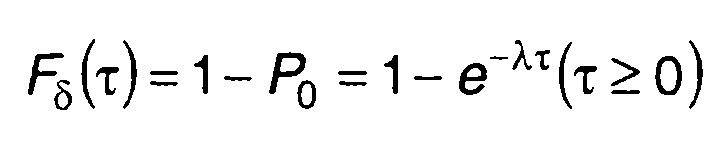(15.53)

представляет одномерную ФРВ длительности интервалов между пе­ресечениями случайным процессом нулевого уровня (рис. 15.7,6). Полученный результат относится только к случайному процессу с пуассоновским распределением нулей (точек пересечения с нуле­вым уровнем).

ПРВ интервалов между точками пересечения:

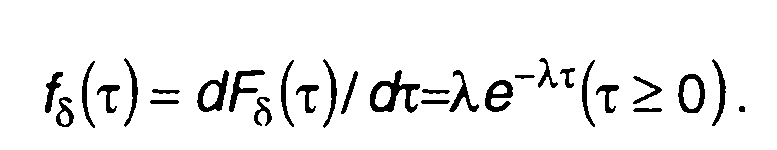(15.54)

Полученное распределение называется показательным с пара­метром λ. Математическое ожидание и дисперсия равны

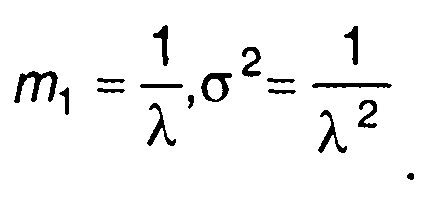(15.55)

15.4. Представление плотности распределения вероятностей случайного процесса с помощью ортогональных многочленов

Плотность распределения вероятностей случайного процесса представляет функцию, которая, как абсолютно интегрируемая, может быть разложена в ряд по ортогональной системе многочле­нов. В некоторых случаях такое представление ПРВ бывает удоб­ным как при анализе самой функции ПРВ, так и при ее расчете.

Примеры применения разложения ПРВ при анализе случайного процесса на выходе нелинейного устройства приведены в разд. 17, 22.

Ряд, в который раскладывается ПРВ, записывается в виде

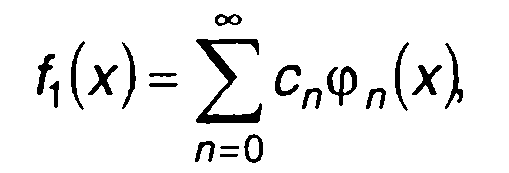(15.56)

где {ф_n(х)} - система базисных функций; с_n - постоянные коэф­фициенты.

В качестве базисных функций ф_л(х) обычно берутся ортого­нальные многочлены. Это связано прежде всего с удобством опре­деления коэффициентов разложения. Система функций {φ_л(х)}

называется ортогональной с весом р (х) на интервале [а, Ь], если выполняется равенство

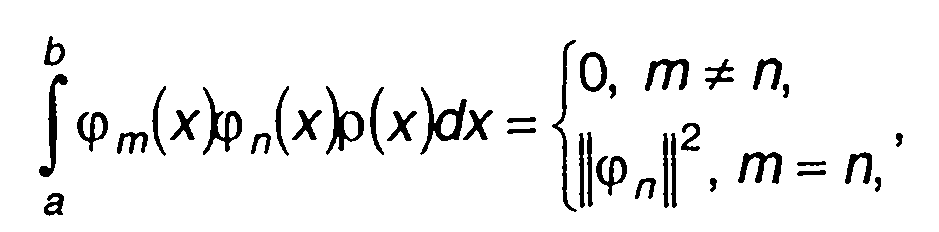(15.57)

где ||φ_n||- норма базисных функций φ_n(х).

Из (15.56) с учетом (15.57) можно определить коэффициенты с_п

как

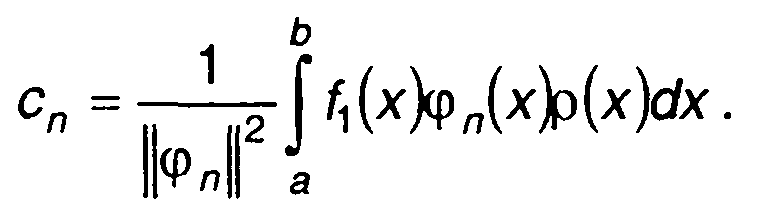(15.58)

В качестве ортогональных многочленов могут быть выбраны мно­гочлены Лежандра, Чебышева, Эрмита, Лагерра и др. Их краткое описание и примеры применения при анализе различных функций даны в первой части книги. При разложении ПРВ случайных процес­сов наиболее часто используются многочлены Эрмита и Лагерра.

15.4.1. Разложение ПРВ в ряд по многочленам Эрмита (ряд Г рама - Шарлье)

Удобство применения многочленов Эрмита при разложении ПРВ связано с тем, что от них достаточно просто перейти к нормальной ПРВ и ее производным. Разложение же ПРВ в ряд с использовани­ем нормальной ПРВ позволяет оперировать с хорошо известной функцией и, кроме того, судить о степени приближения рассматри­ваемой ПРВ к нормальной, установить условия, при которых это приближение будет более близким.

Многочлены Эрмита, применяемые при разложении ПРВ, обыч­но определяются как

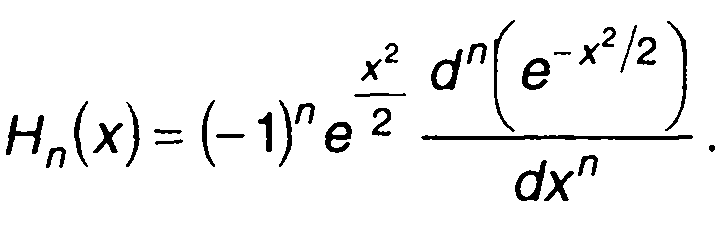(15.59)

Они ортогональны на всей оси (-∞;∞ ) с весом е^-x2/2:

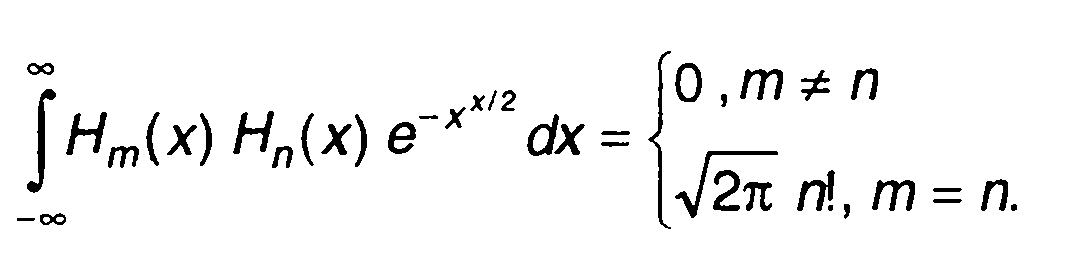
Первые шесть многочленов:

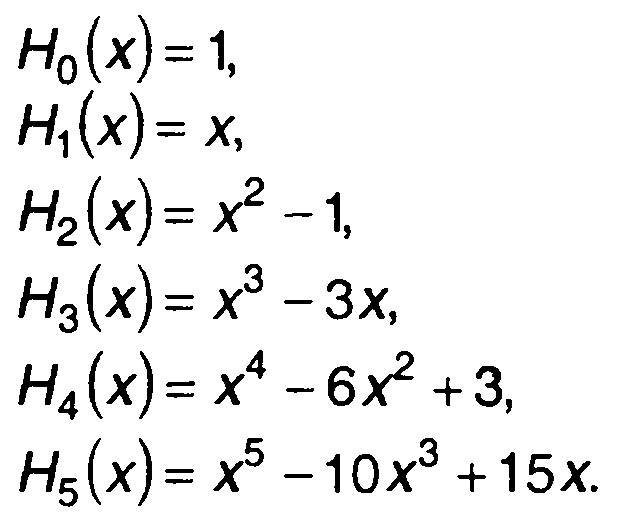(15.60)

Многочлены Эрмита связаны с нормальной ПРВ

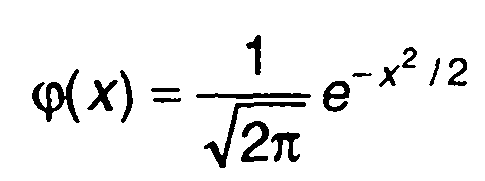
и ее производными φ(n)(х) соотношением

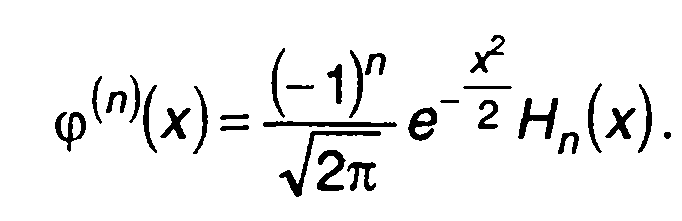(15.61)

Функции Нn(х) и φ(n)(х) являются ортогональными, для них справедливо равенство

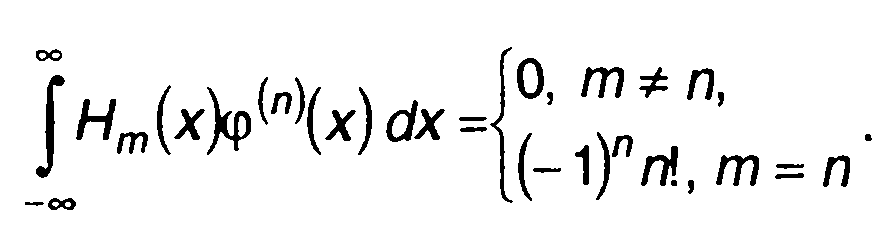(15.62)

Вследствие этого возможно представление f1(х) в виде ряда разложения по функциям φ⁽ⁿ⁾(х)

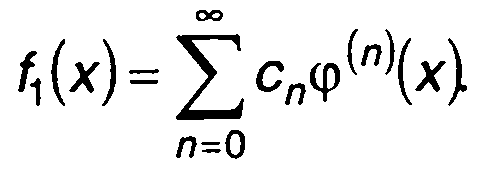(15.63)

Умножение левой и правой частей (15.63) на Н_n(х) и интегриро­вание от -∞ до ∞ приводят к следующему выражению для коэф­фициентов ряда:

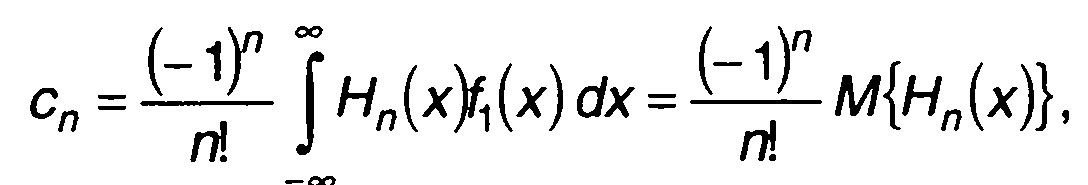(15.64)

где M(....) - символ усреднения.

Таким образом, коэффициенты ряда определяются математиче­ским ожиданием многочленов Эрмита, а с учетом выражений для них (15.60) - начальными моментами случайной величины (случай­ного процесса в выбранный момент времени)

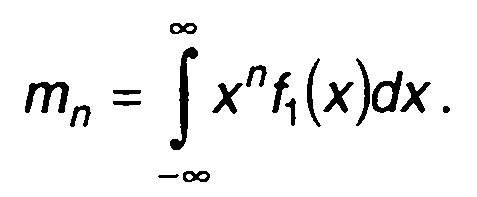(15.65)

Функция ф(х) представляет нормальную ПРВ случайной вели­чины с нулевым математическим ожиданием и единичной диспер­сией. При переходе к ПРВ с произвольными значениями ма­тематического ожидания и дисперсии выражение (15.63) должно быть заменено следующим (см. п. 15.5.):

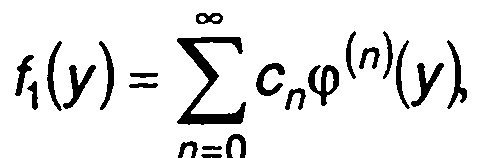(15.66)

а (15.64):

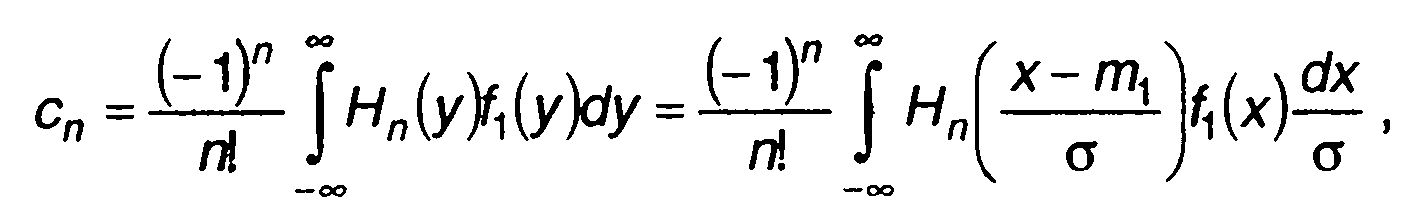(15.67)

где m₁, σ² - математическое ожидание и дисперсия случайной ве­личины,

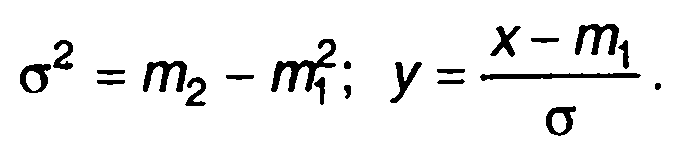
Первые коэффициенты разложения равны

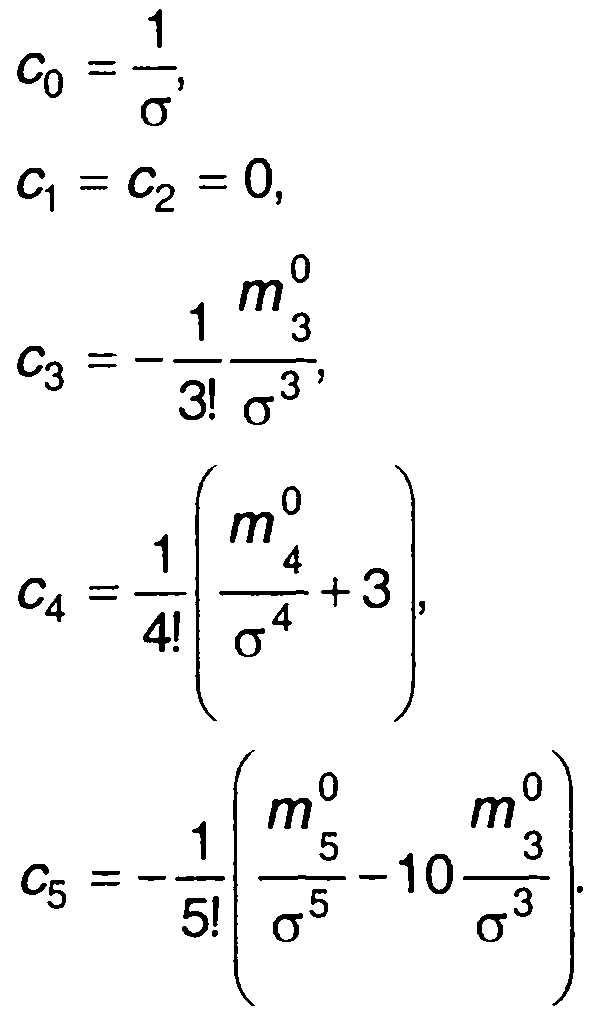(15.68)

Таким образом, выражение для ПРВ примет вид

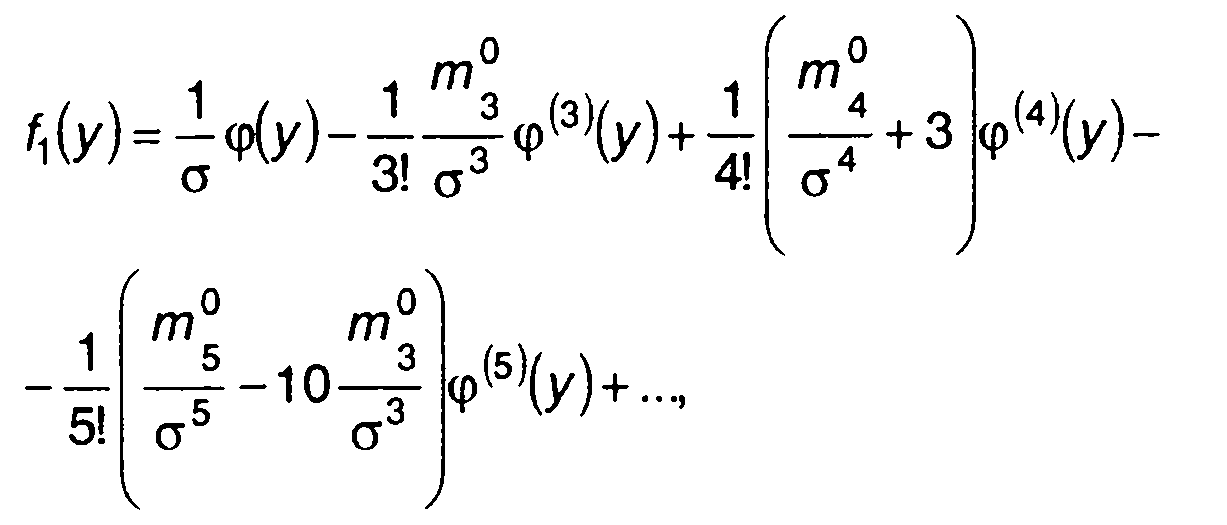(15.69)

где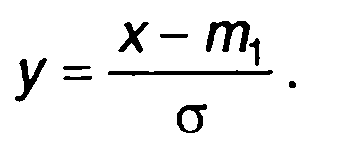

Разложение ПРВ в виде (15.69) представляет ряд Грама- Шарлье. Последовательность получения такого разложения - сле­дующая: находятся начальные моменты распределения случайного процесса; в соответствии с (15.18) определяются центральные мо­менты и определяются коэффициенты разложения (15.67); записы­вается ряд в виде (15.69).

Функции φ⁽ⁿ⁾(у) табулированы. Пример разложения ПРВ в ряд Грама-Шарлье дан в разд. 17.

15.4.2. Разложение ПРВ в ряд по многочленам Лагерра

Многочлены Лагерра при описании ПРВ определяются выраже­нием

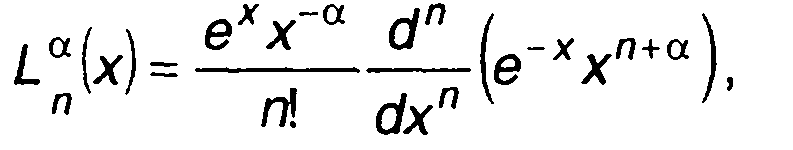(15.70)

первых порядков:

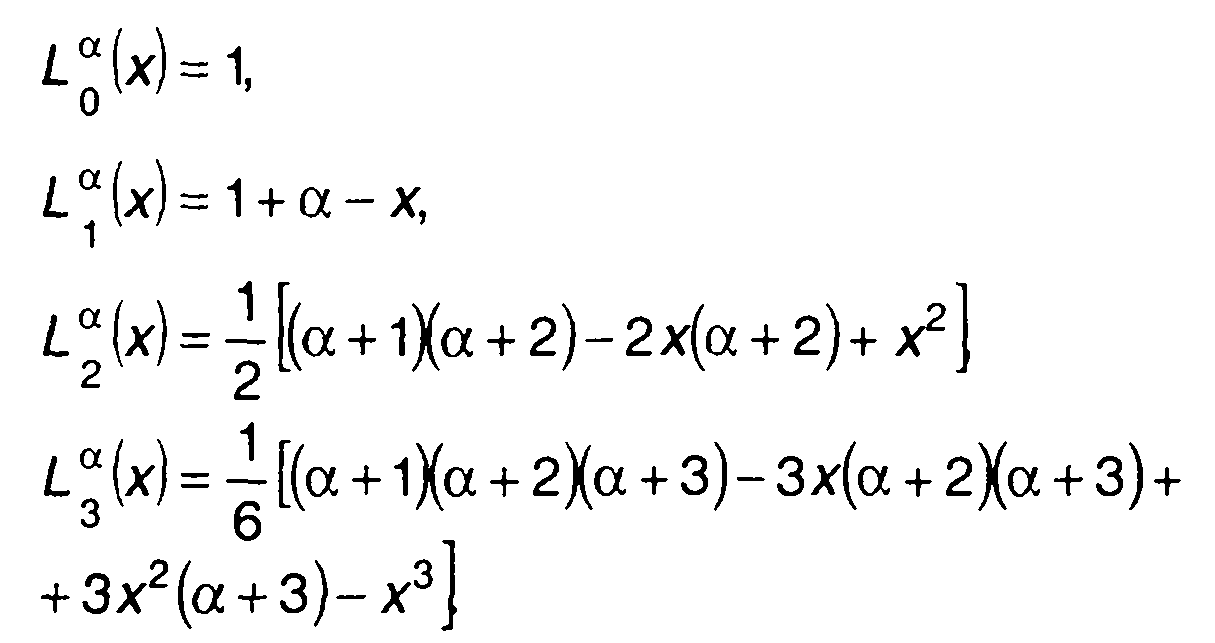(15.71)

Многочлены Лагерра ортогональны на полуоси [0, ∞) с весом

е^-хх^а

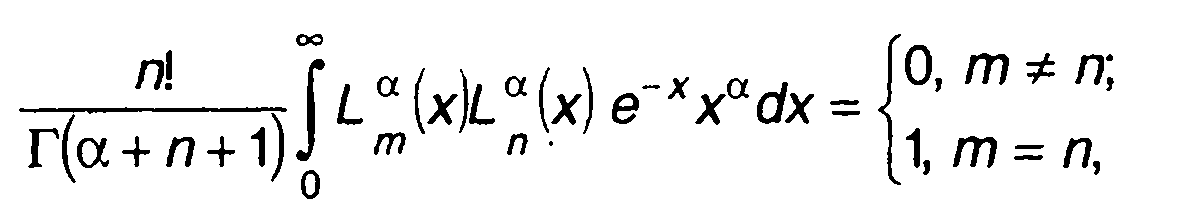(15.72)

где Г(х) - гамма-функция.

Разложение ПРВ неотрицательной случайной величины в ряд по многочленам Лагерра записывается в виде

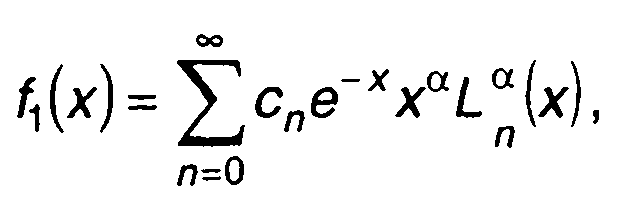(15.73)

где коэффициенты с_n определяются выражением

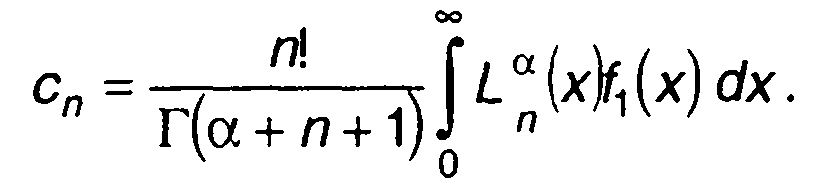(15.74)

Выражение (15.74) получается из (15.73) с учетом (15.72). При

переходе к новой переменной у = x/β запишем

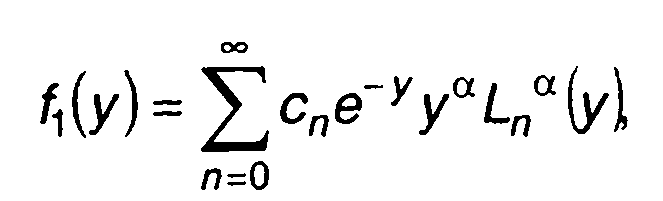(15.75)

где

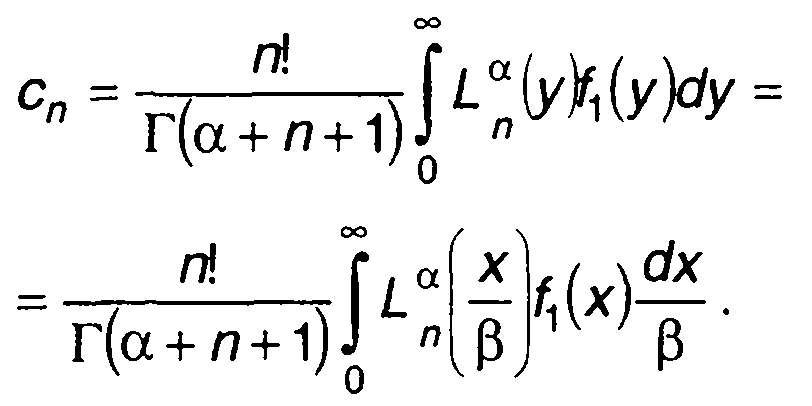(15.76)

Из (15.76) с учетом (15.71) найдем

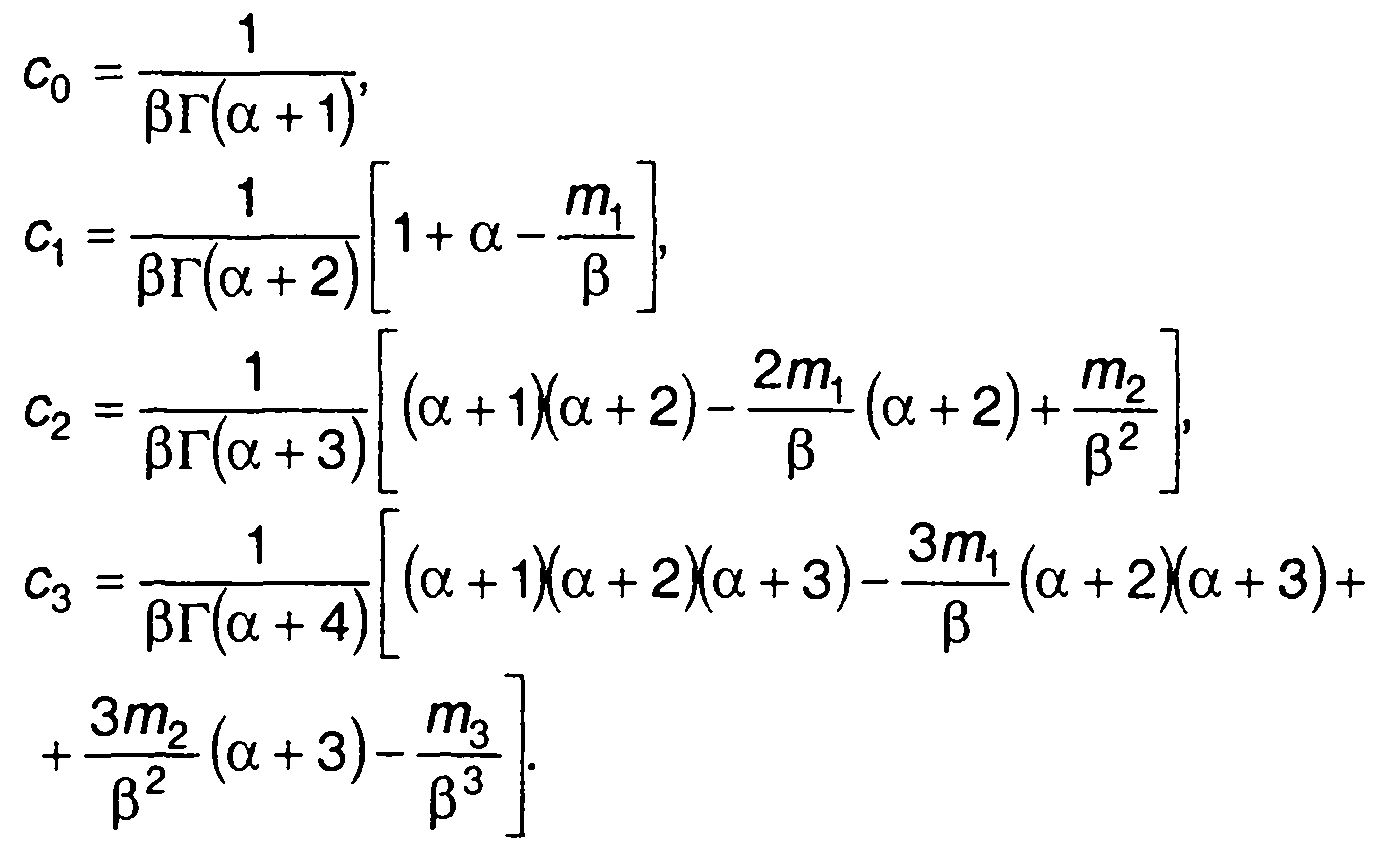(15.77)

Константы а и β выбираются таким образом, чтобы коэффици­енты с₁ и с₂ были равны нулю. Это условие выполняется при

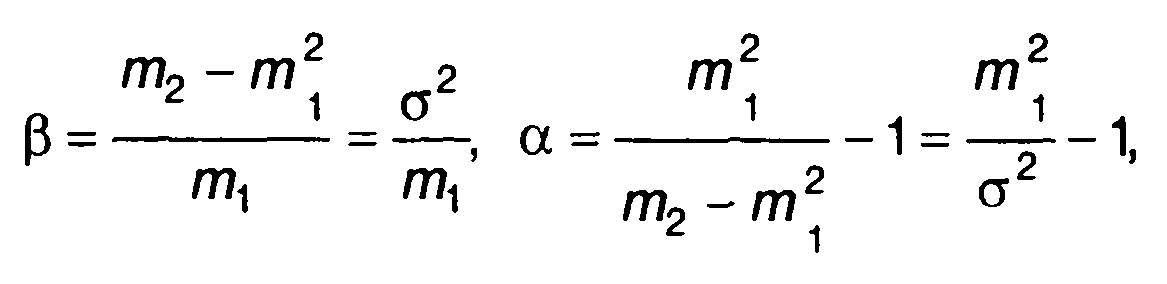(15.78)

где σ² - дисперсия случайной величины.

Таким образом, имеем:

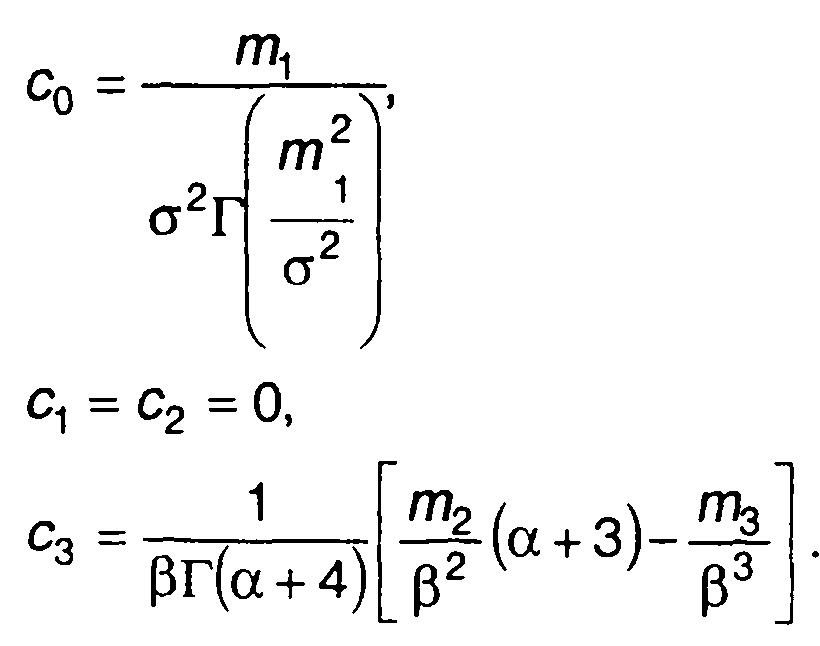(15.79)

Коэффициенты разложения, начиная с с₃, определяются до­вольно сложными выражениями. Вследствие этого представление ПРВ в виде ряда Лагерра обычно используется только в том слу­чае, когда можно ограничиться только одним первым членом. В этом случае

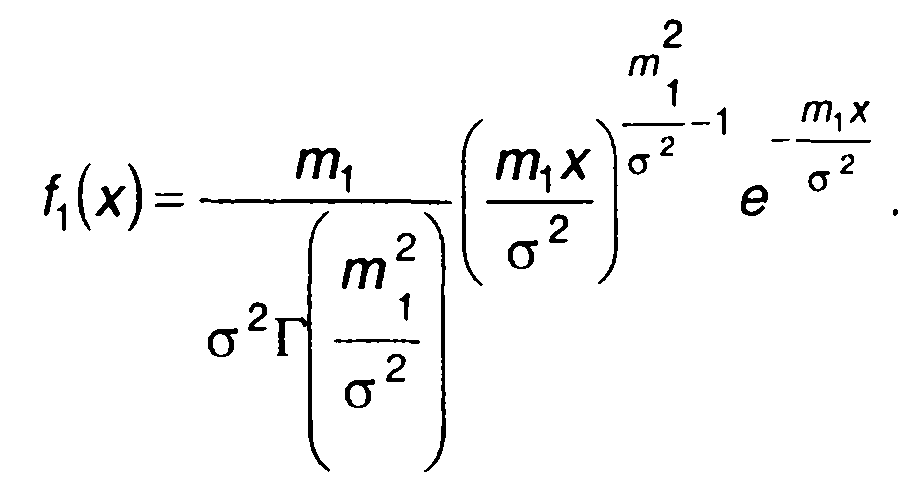(15.80)

Пример использования приведенного представления ПРВ дан в разд. 17.

15.5. Одномерное распределение вероятностей функции случайного процесса

В цепях радиотехнических систем происходит преобразование случайного колебания - случайного процесса. Появляется необхо­димость определения характеристик случайного процесса после его преобразования.

Если случайные величины ξ(t) и η(t) связаны однозначным со­отношением (рис. 15.8,а)

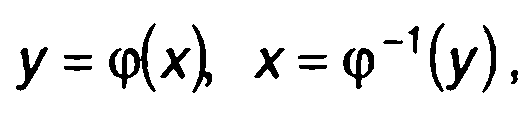(15.81)

где φ¹(у) - функция, обратная ф(х),

то это означает, что каждому значению х, принимаемому случайной величиной ξ(t), соответствует единственное значение у, прини­маемое η(t). Вероятность попадания случайной величины ξ(t) в интервал [х, х + dx] равна вероятности попадания случайной вели­чины тi(f) в интервал [у, у + dy]. Таким образом, (рис. 15.8,б)

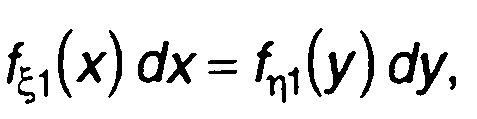(15.82)

где f_ξ (х),f_η1 (у) - одномерные ПРВ случайных величин ξ(t) и η(t).

От (15.82) можно перейти к следующему соотношению, связы­вающему ПРВ случайной величины ξ(t) с ПРВ η(t),

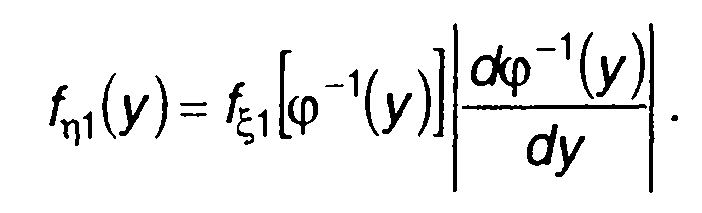(15.83)

Если обратная функция х=φ^-1(у) неоднозначна, то одному зна­чению у соответствует несколько значений х: х₁(у), х₂(у),...., х_п(у). В этом случае выражение (15.83) должно быть записано в виде

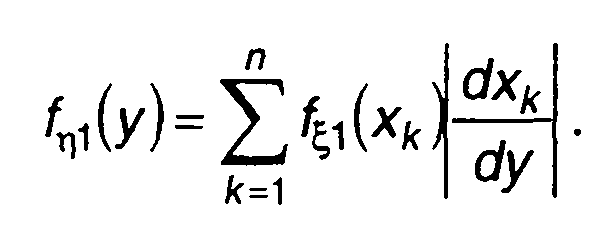(15.84)

С учетом (15.83) можно получить моменты функции случайной величины. Если обратная функция φ^-1(у) однозначная, то с учетом (15.82) можно записать

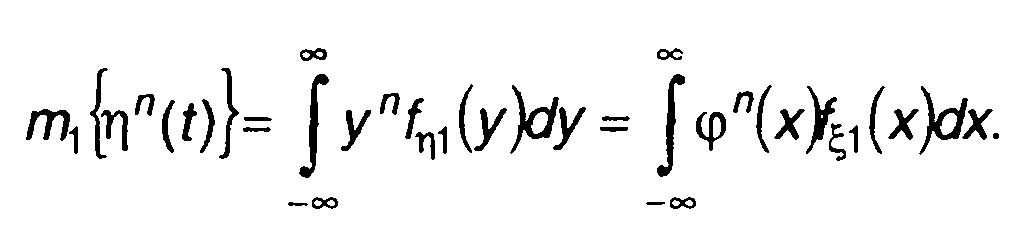(15.85)

В качестве примеров рассмотрим некоторые виды преобразова­ний случайных процессов, с которыми приходится иметь дело на практике.

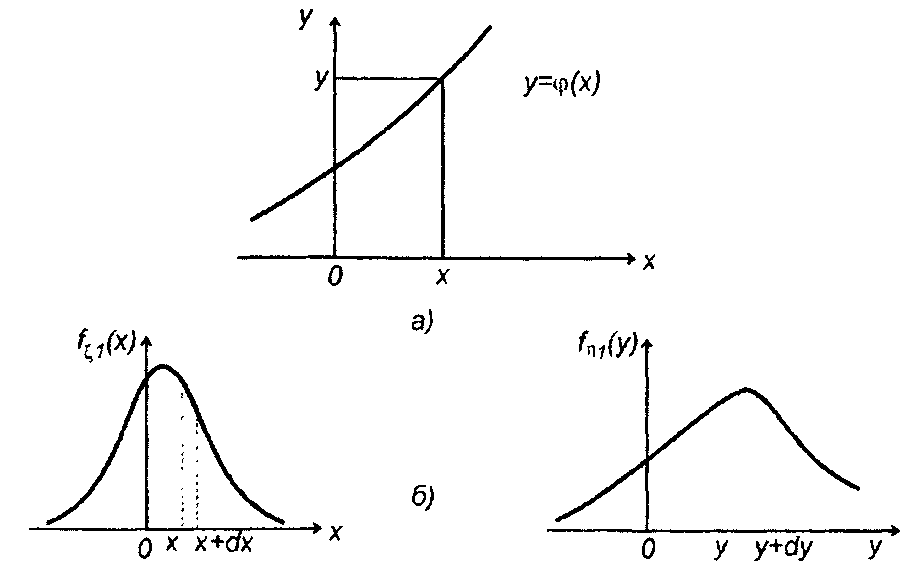
Рис.15.8

1. Линейное преобразование (табл. 15.2, п.1).

При линейном преобразовании случайной величины

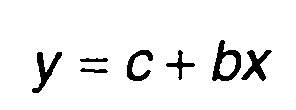(15.86)

имеем взаимно однозначное соответствие ξ(t) и η(t). Из (15.83) получим

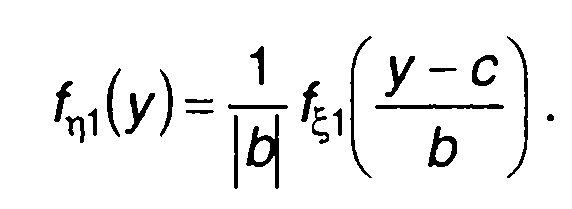(15.87)

Как следует из (15.87), при линейном преобразовании случайной величины происходит смещение кривой ПРВ на с и изменение масштаба по осям координат в b раз.

Для гауссовского процесса

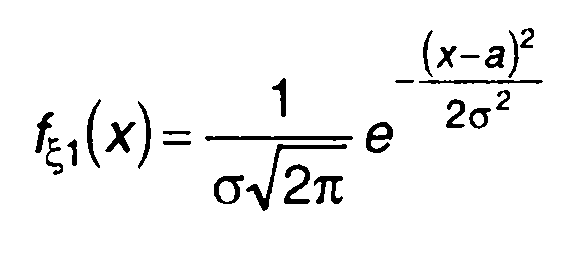(15.88)

получим

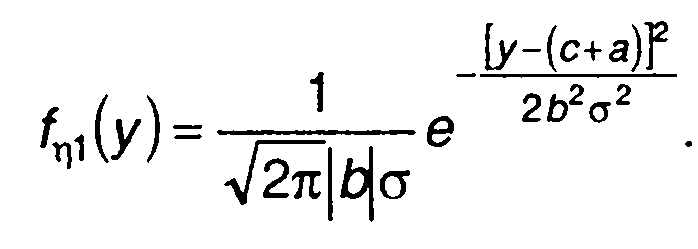(15.89)

Таким образом, линейное преобразование гауссовского процес­са не изменяет закона распределения - случайный процесс остает­ся гауссовским.

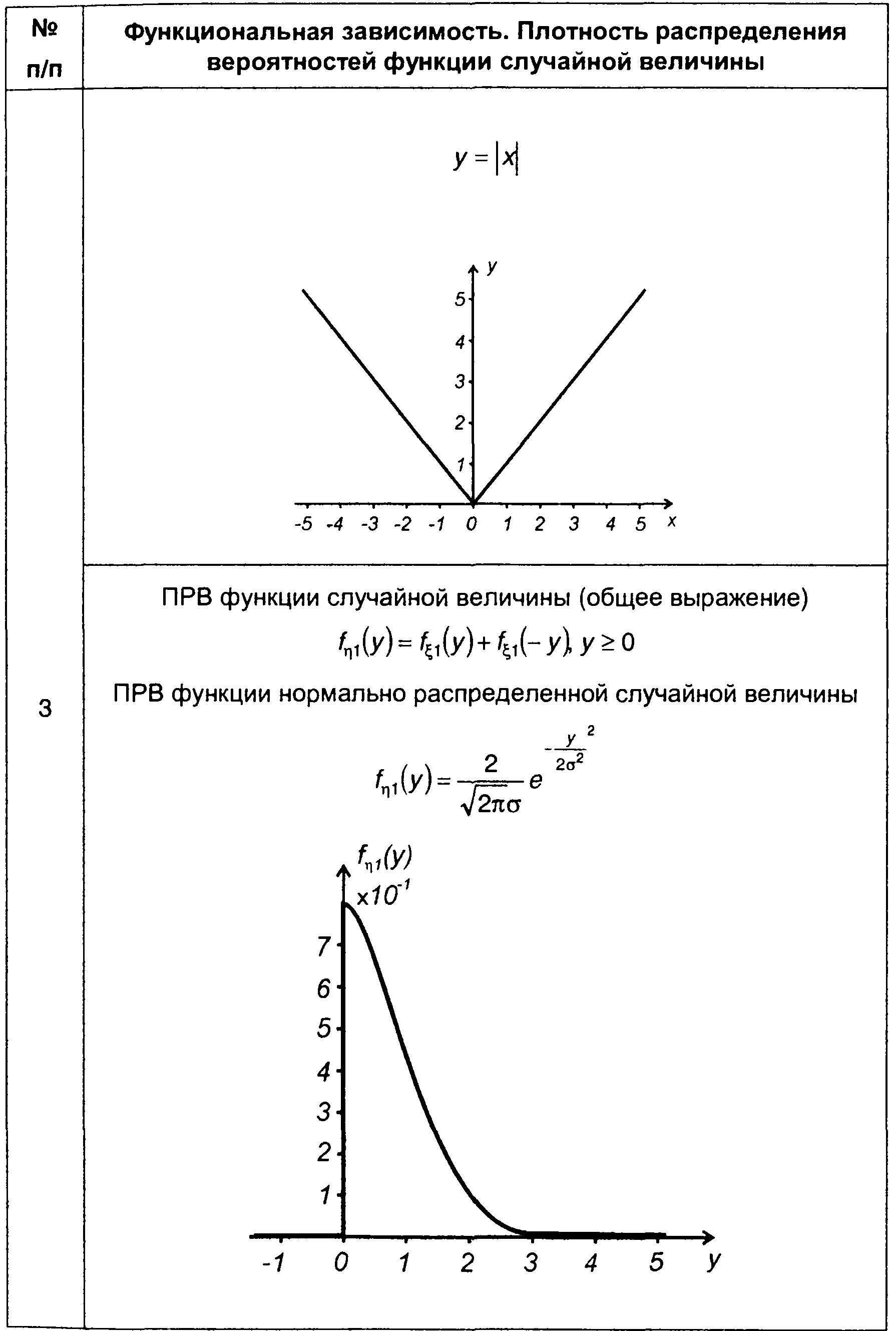
2. Квадратичное преобразование (табл. 15.2, п.4).

При квадратичном преобразовании случайной величины

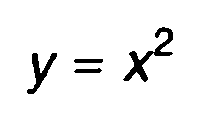(15.90)

каждому значению у соответствуют два значения х

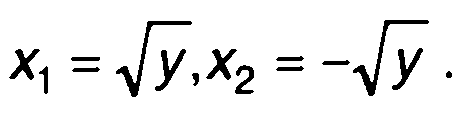(15.91)

Из (15.84) с учетом (15.91) найдем

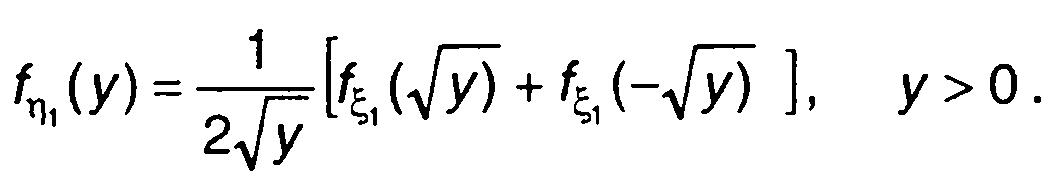(15.92)

Таблица 15.2

Плотность распределения вероятностей функции случайной величины

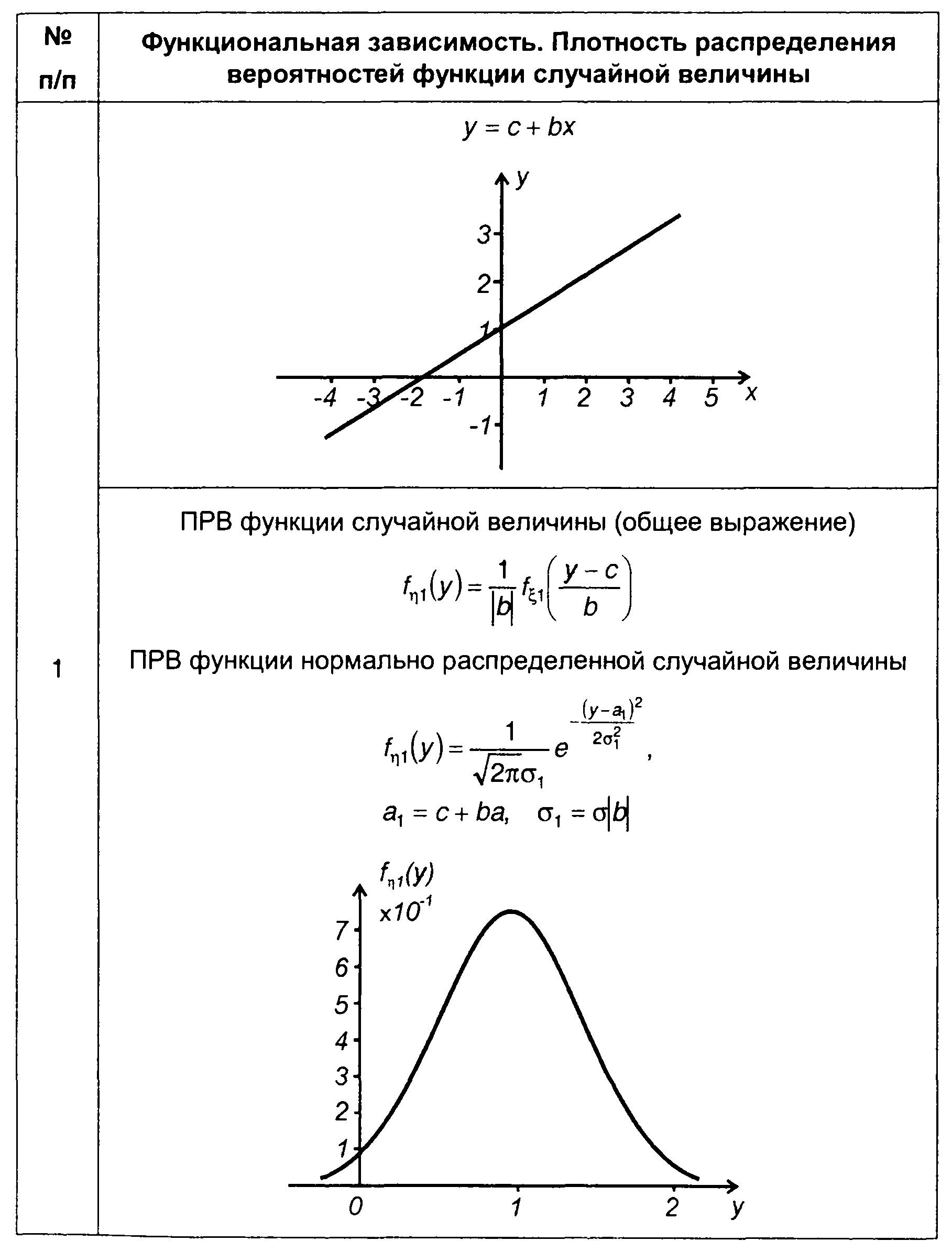
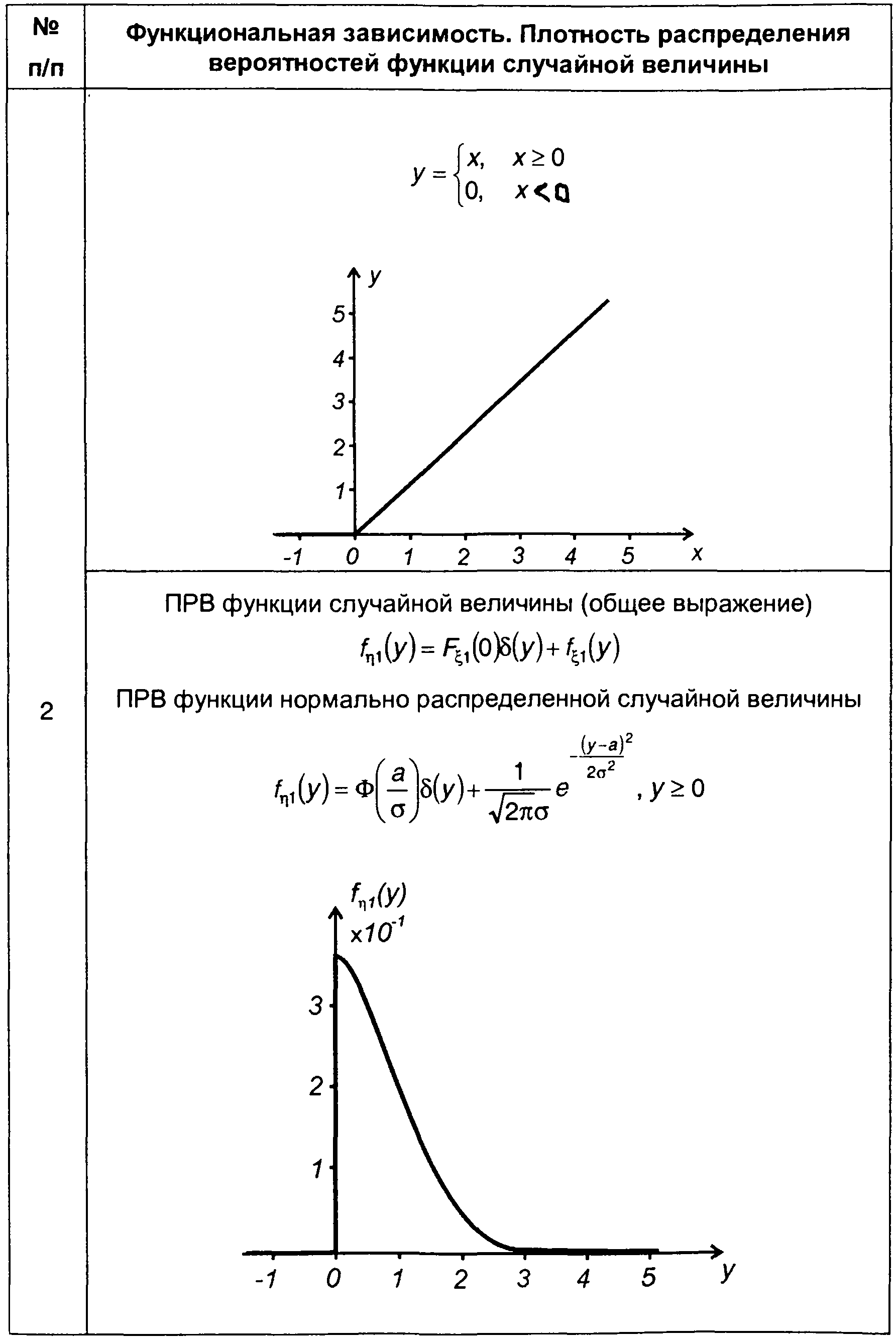
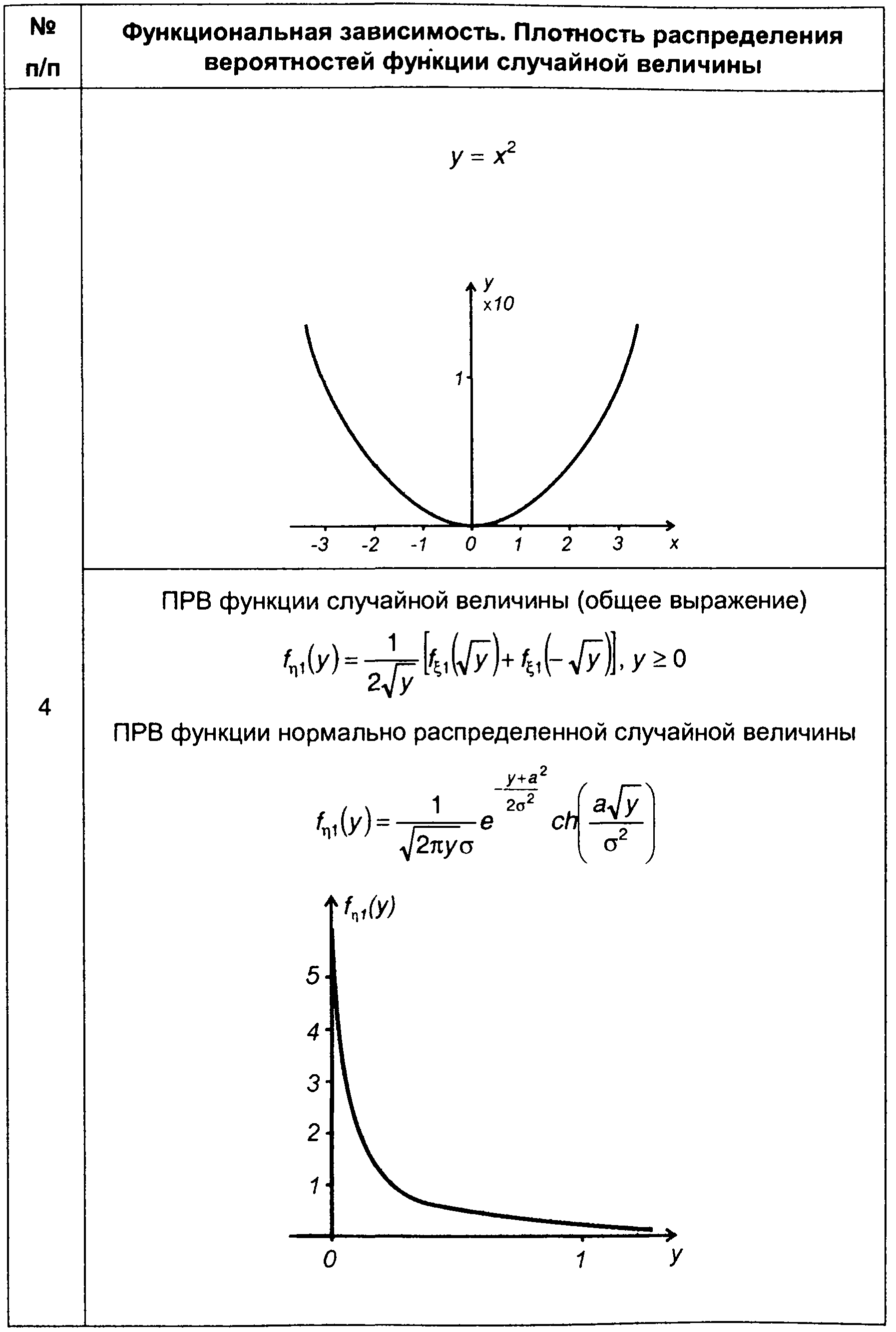
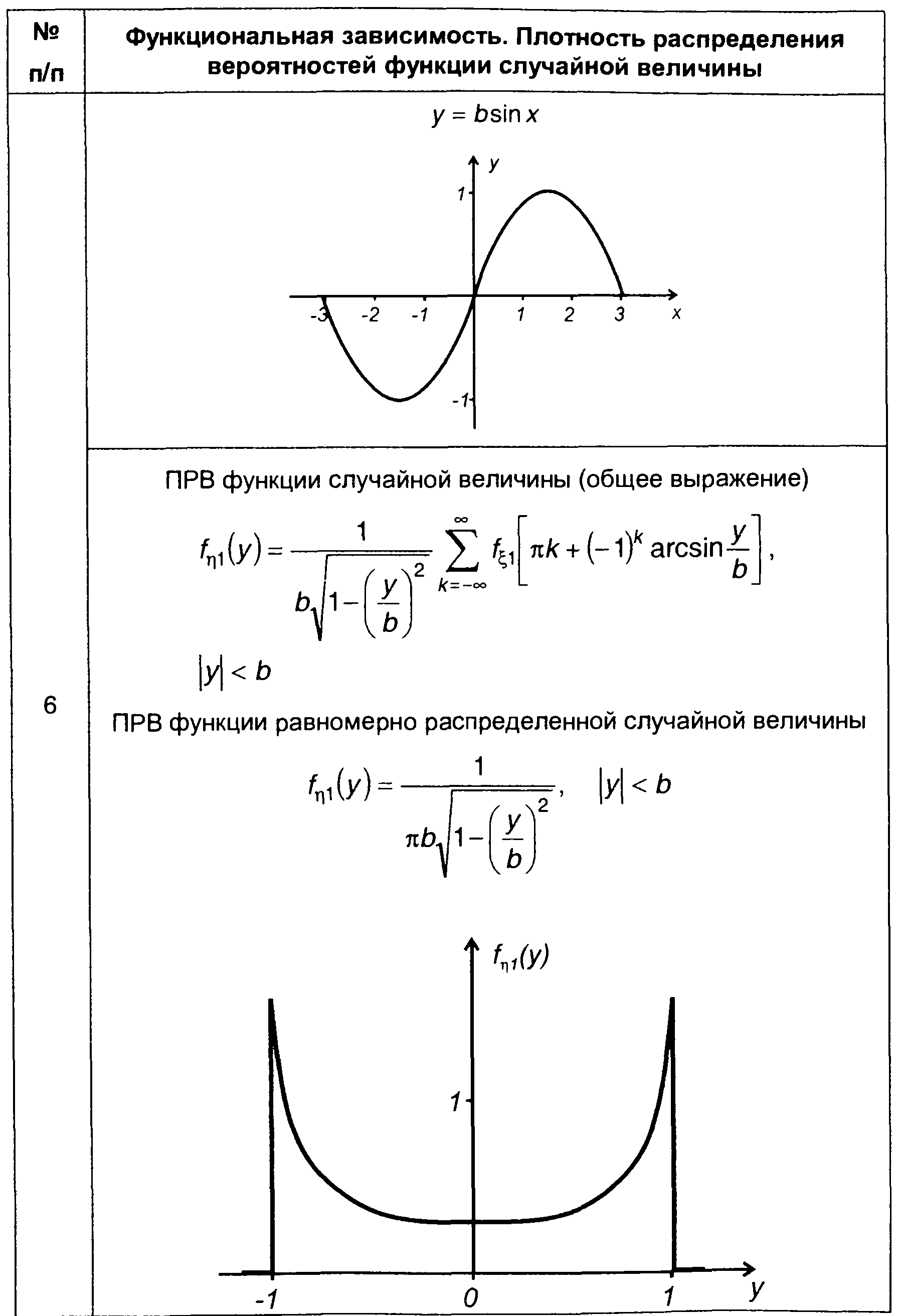
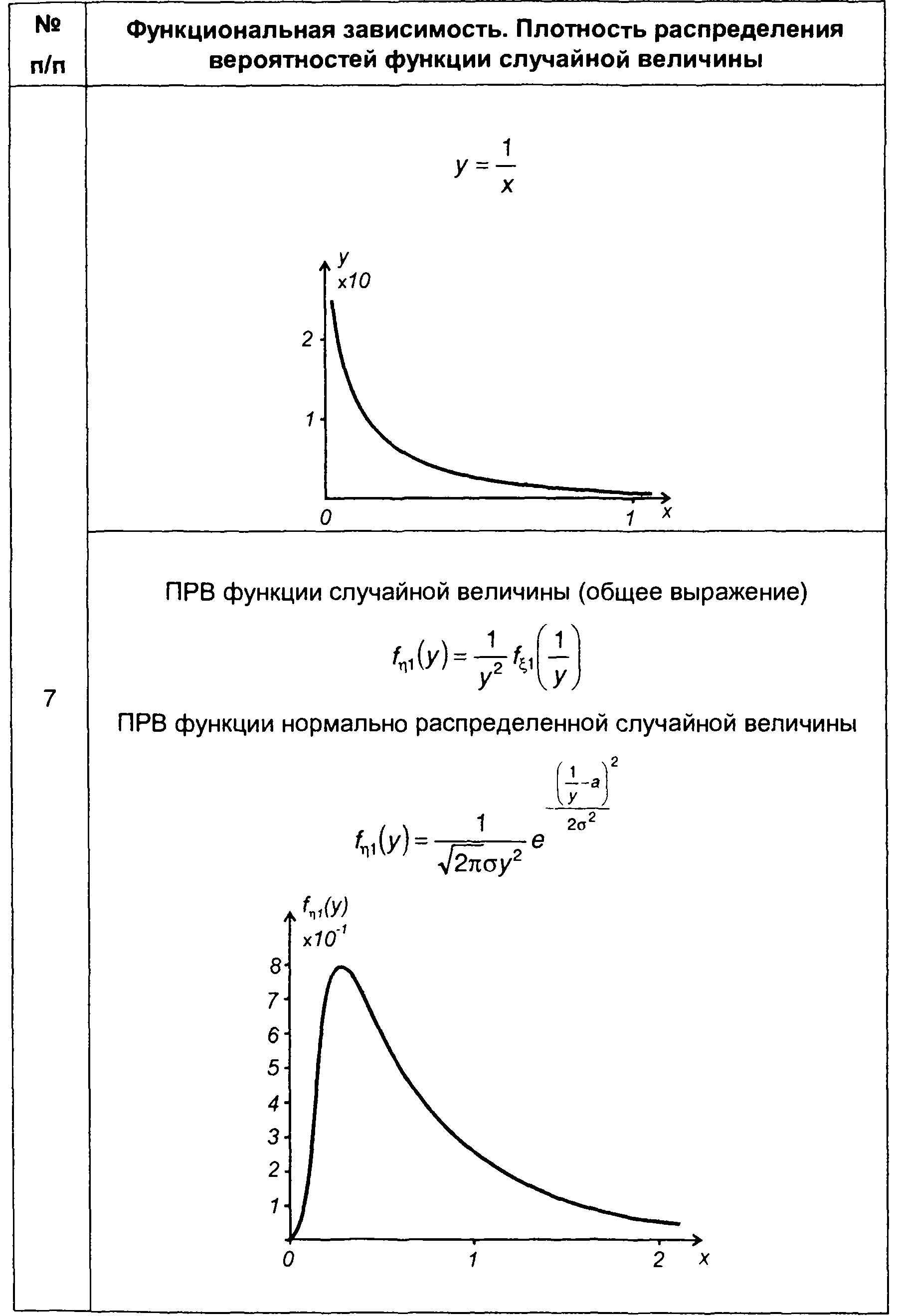
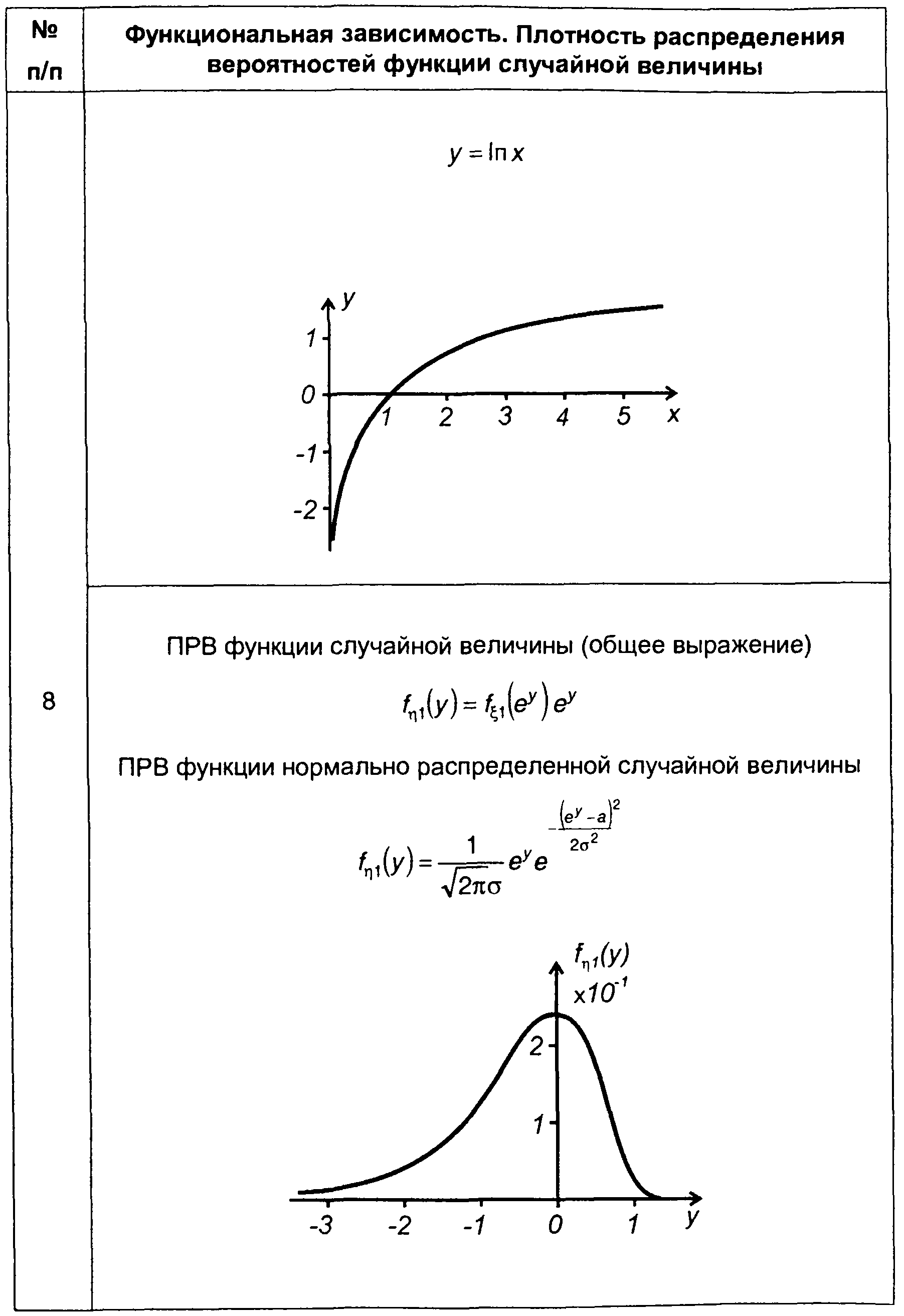
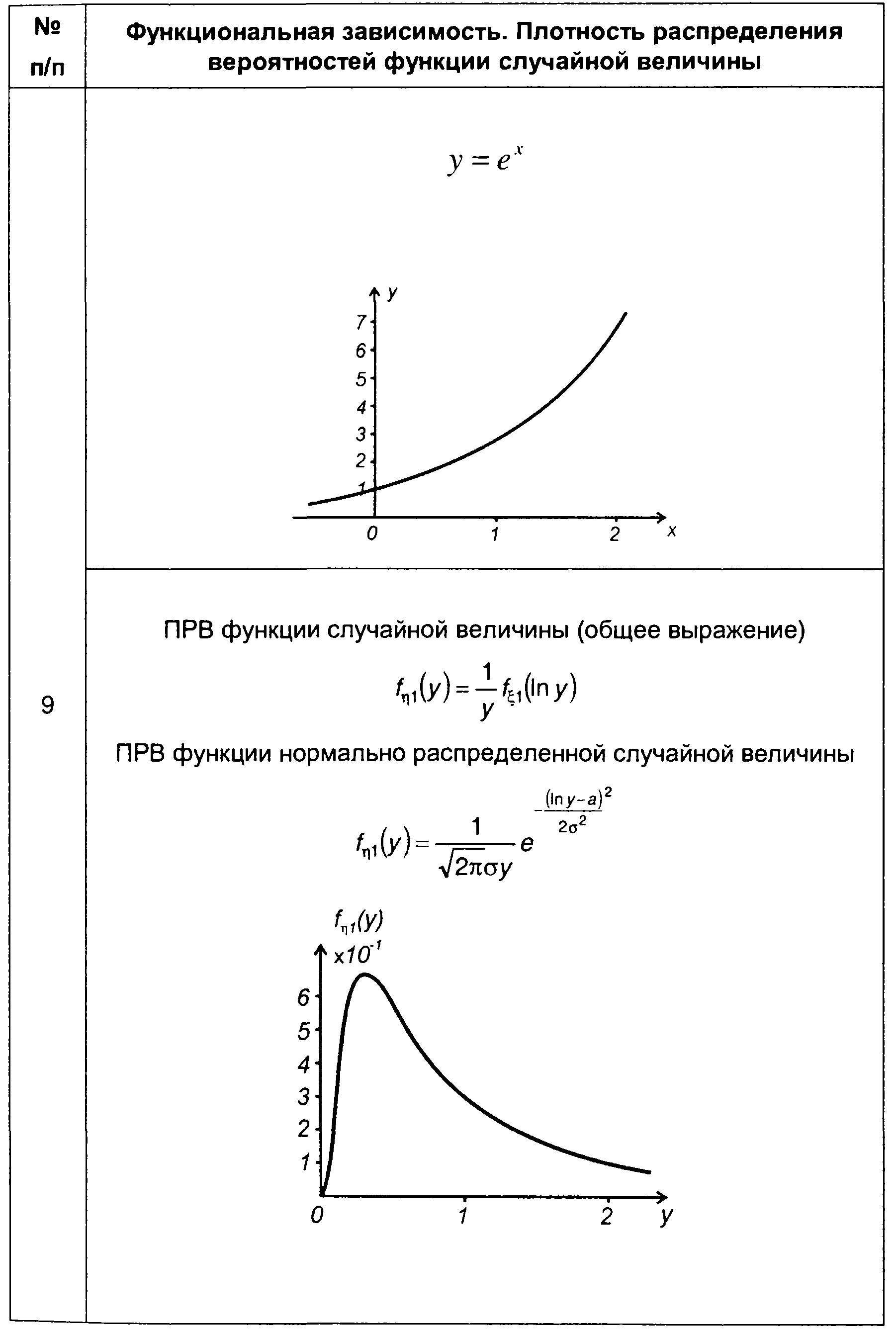
Для гауссовского процесса из (15.92) получим

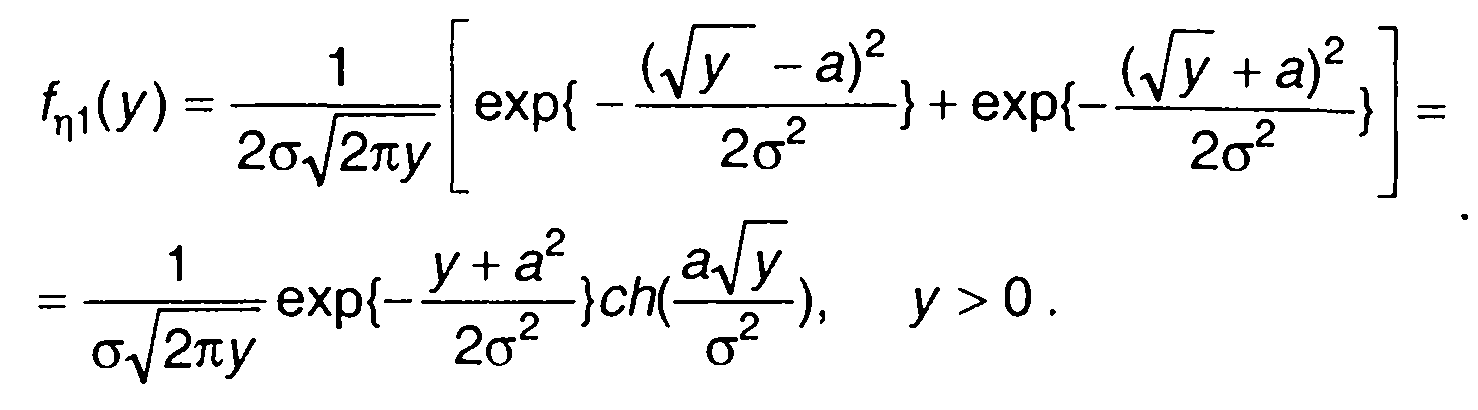(15.93)

При а = 0 (рис. 15.9,б)

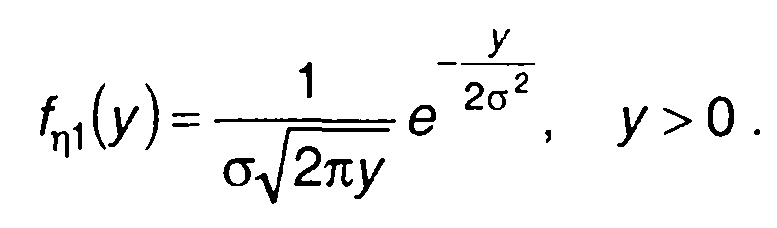(15.94)

Для релеевского процесса

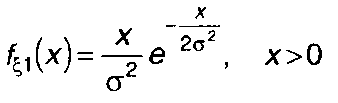(15.95)

получим (рис. 15.9,в)

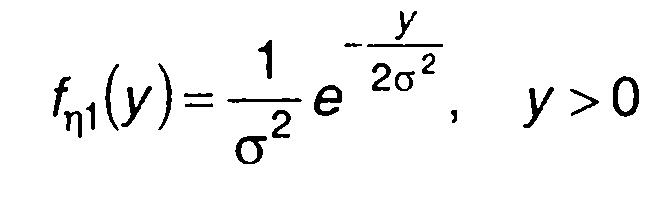(15.96)

Случайный процесс η(t) в этом случае имеет экспоненциальное

распределение (табл. 15.1).

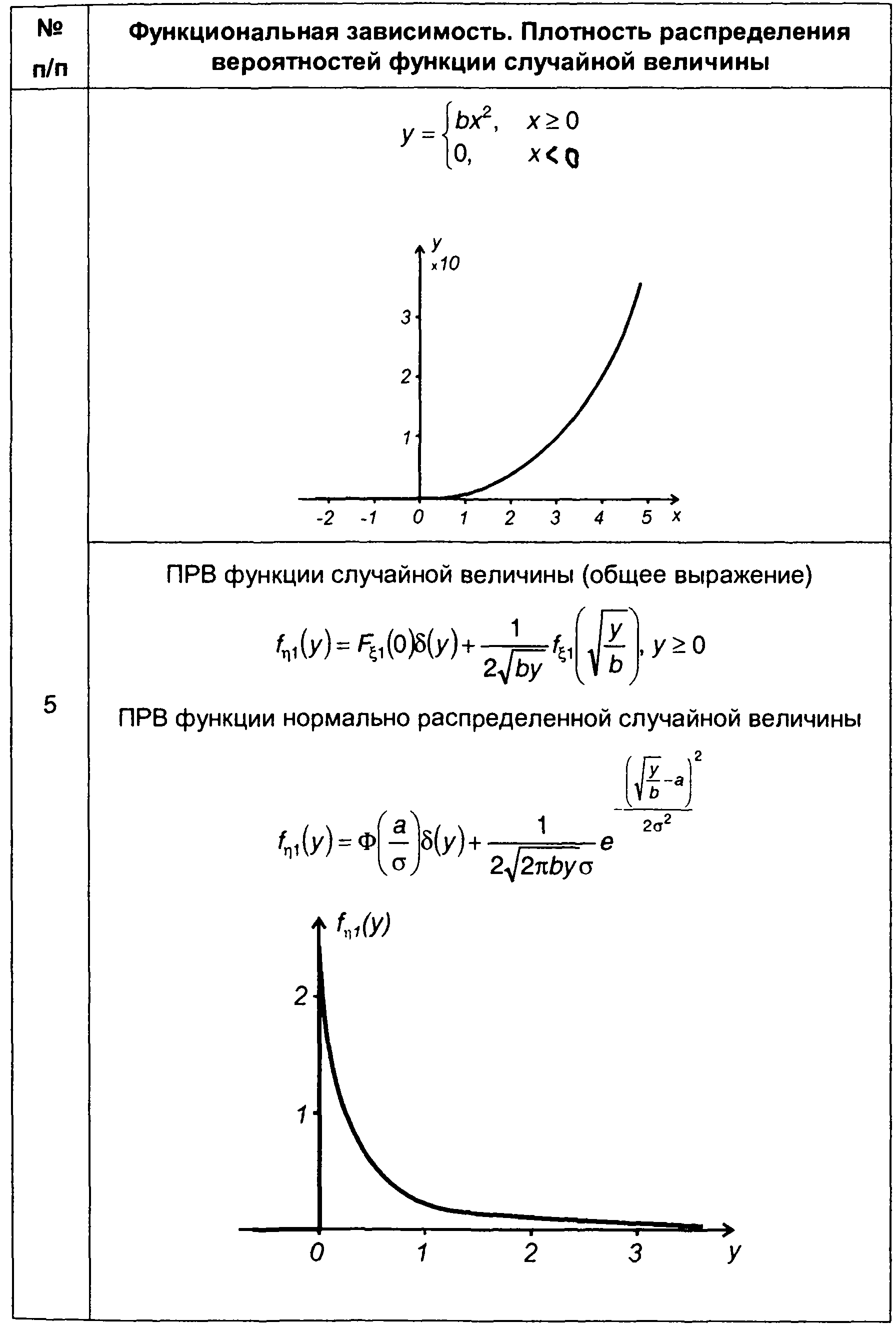
3. Преобразование (табл. 15.2, п.6)

(15.97)

Каждому значению у соответствует бесчисленное множество значений х:

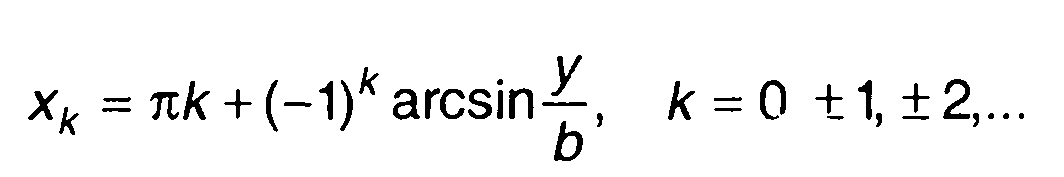(15.98)

Из (15.84) с учетом (15.98) найдем

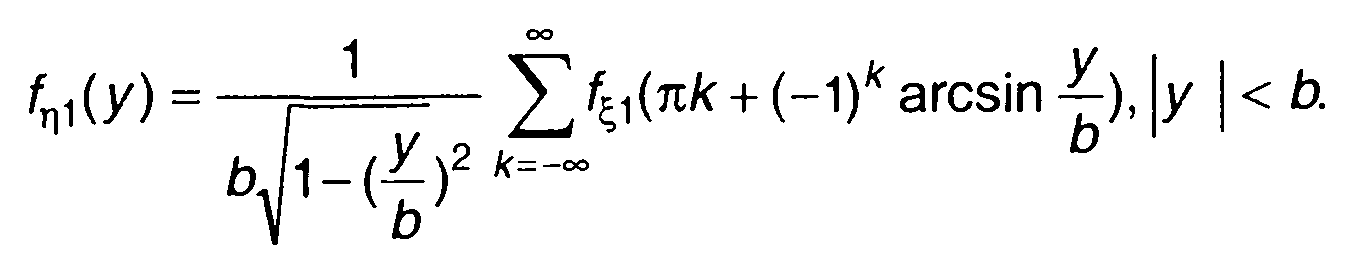(15.99)

Наибольший интерес представляет равномерное распределе­ние ξ на интервале |x| ≤ π

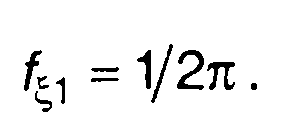(15.100)

В этом случае в (15.99) необходимо учесть три члена - при k = -1, k = 0 и k= 1 ПРВ случайной величины η(t) примет вид

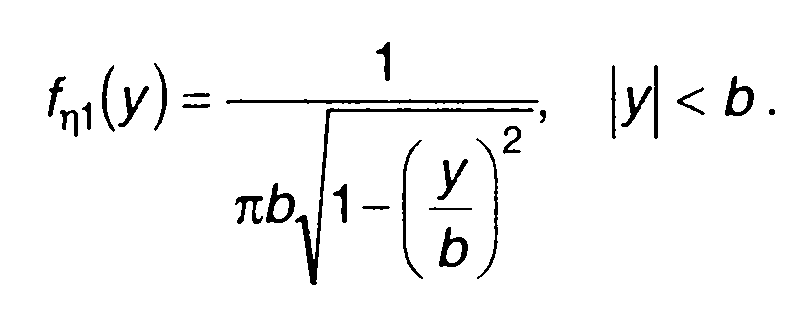(15.101)

ФРВ, соответствующая (15.101), равна

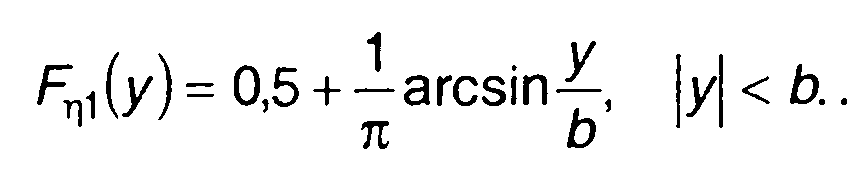(15.102)

Некоторые наиболее простые функции случайных величин и со­ответствующие ПРВ приведены в табл. 15.2.

15.6. Характеристическая функция случайного процесса

Удобной характеристикой случайных процессов, широко исполь­зуемой при их анализе, является характеристическая функция. Ха­рактеристическую функцию случайного процесса ξ(t) обычно опре­деляют как математическое ожидание функции e^ivξ(t) где v- про­извольная действительная величина

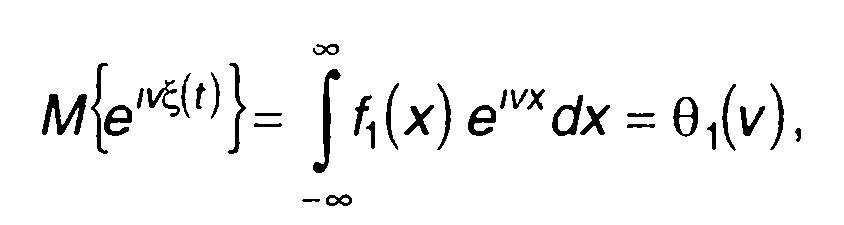(15.103)

где f₁(х) - ПРВ случайного процесса ξ(t).

Как следует из (15.103), характеристическая функция является обратным преобразованием Фурье ПРВ случайного процесса (без привычного коэффициента 1/2π). Прямое преобразование Фурье характеристической функции (с коэффициентом 1/2π) дает ПРВ случайного процесса.

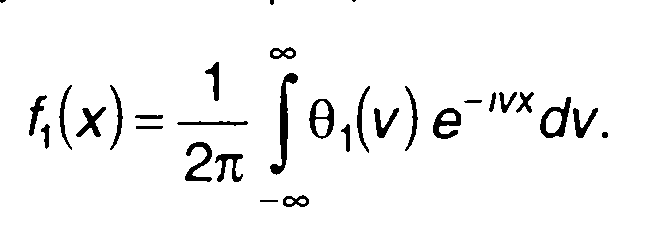(15.104)

Таким образом, ПРВ и характеристическая функция случайного процесса связаны преобразованием Фурье (прямым и обратным). Характеристическую функцию можно также определить как обратное преобразование ПРВ случайного процесса (случайной величины).

Так как |e^ivξ(t)| = 1 при всех действительных v, интеграл (15.103)

существует для всех ПРВ, следовательно, характеристическая функция может быть определена для каждой случайной величины. Для характеристической функции справедливы следующие соот­ношения:

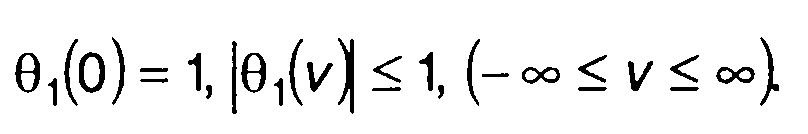(15.105)

Если ПРВ четная, то соответствующая характеристическая функция является действительной функцией.

В качестве примера определим характеристическую функцию га­уссовского процесса. Она получается подстановкой (15.23) в (15.103)

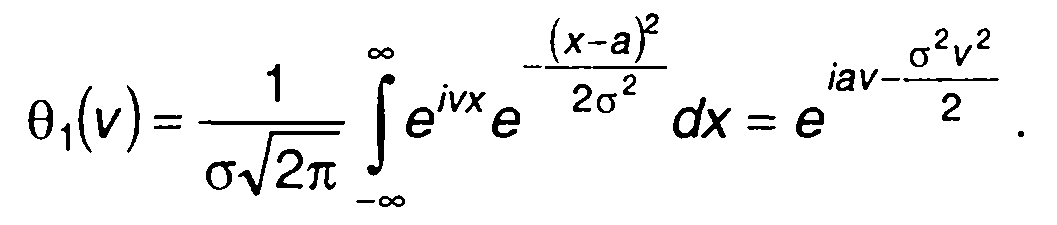(15.106)

Для центрированного гауссовского процесса имеем

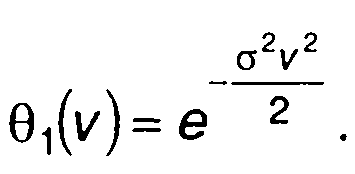(15.107)

Выражения для характеристических функций при некоторых других видах распределения случайной величины приведены в табл. 15.1. Если η= bξ + а, (b и а - постоянные), то

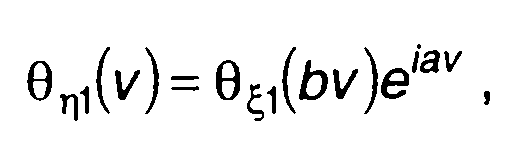(15.108)

где Θ_ξ1(v) и Θ_η1(v) - характеристические функции случайных вели­чин ξ и η.

Действительно,

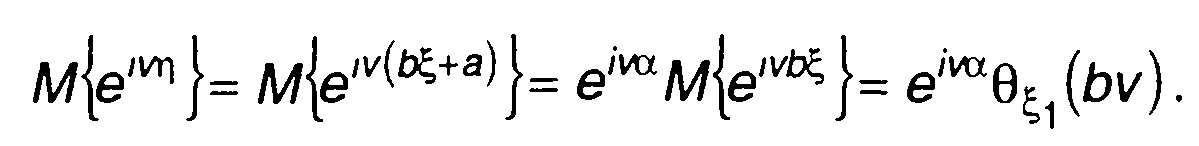(15.109)

Удобство использования характеристической функции при ана­лизе случайных процессов следует из свойств преобразования Фу­рье. В частности, характеристическая функция суммы независимых

случайных величин равна произведению их характеристических функций.

Производные характеристической функции по параметру v оп­ределяются выражением

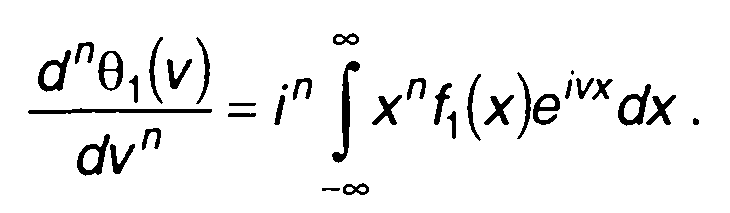(15.110)

Если существует начальный момент n-го порядка случайного процесса, то из (15.110) получим

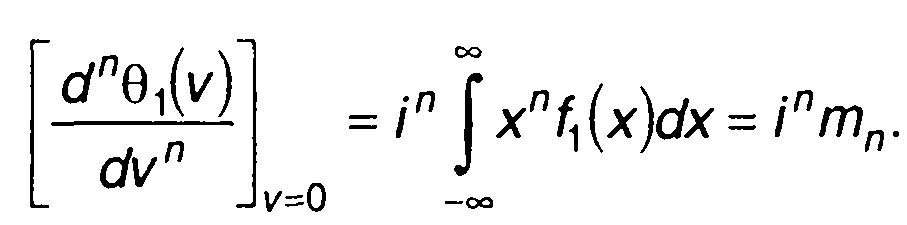(5.111)

Таким образом, начальные моменты случайного процесса мож­но определить через производные характеристической функции при v=0

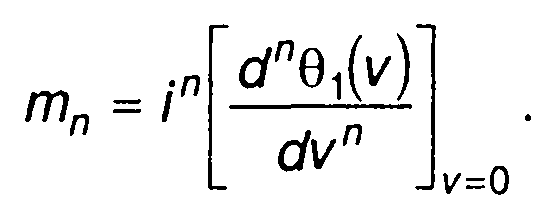(15.112)

Раскладывая характеристическую функцию в ряд Тейлора, запи­шем

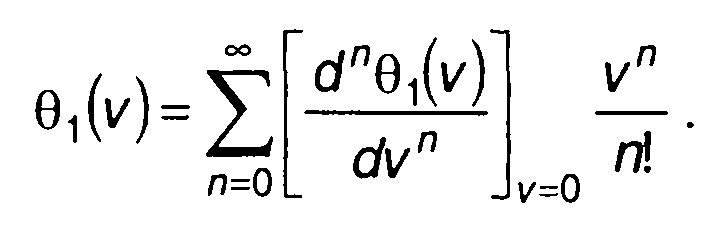(15.113)

С учетом (15.113) получим

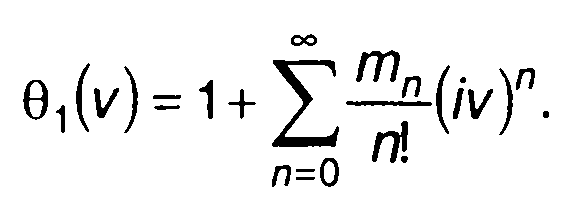(15.114)

Следовательно, характеристическая функция случайного про­цесса определяется моментами распределения. Учитывая связь характеристической функции с ПРВ, можно сказать, что моменты распределения вероятностей определяют и ПРВ случайного про­цесса. Чем большее число начальных моментов распределения случайного процесса известно, тем точнее может быть определена характеристическая функция и ПРВ случайного процесса.

достаточно просто определяются через производные логарифма характеристической функции.

Обозначим

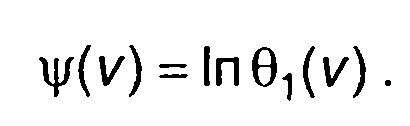
Получим

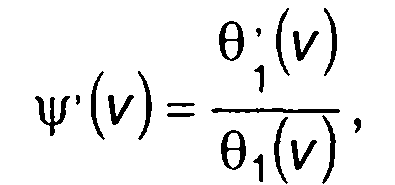(15.115)

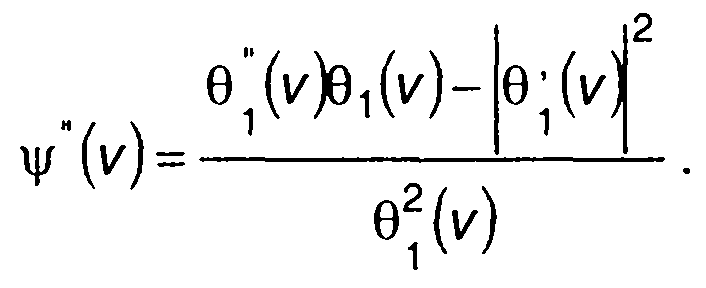(15.116)

Учитывая, что Θ₁(0) = 1, и (15.111), находим:

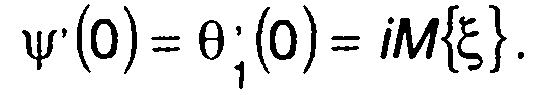(15.117)

Таким образом,

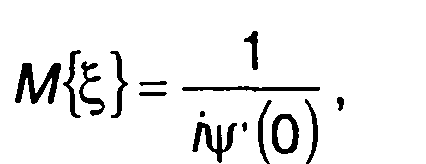(15.118)

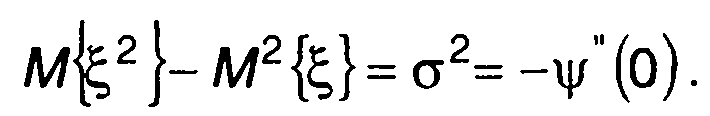(15.119)

Производная n-го порядка логарифма характеристической функ­ции при v = 0, умноженная на iⁿ, называется семиинвариантом n-го порядка случайной величины.

Соотношения, аналогичные полученным выше, позволяют убе­диться в том, что семиинварианты любого порядка n представляют действительную функцию n первых моментов.

Раздел 16.

МНОГОМЕРНОЕ РАСПРЕДЕЛЕНИЕ ВЕРОЯТНОСТЕЙ СЛУЧАЙНОГО ПРОЦЕССА

Наиболее полное описание случайного процесса на интервале времени дает п-мерная ФРВ или ПРВ. Они характеризуют стати­стически поведение случайного процесса в выбранные моменты времени. Используя п-мерные ФРВ и ПРВ, можно получить мо­менты распределения вероятностей и другие характеристики слу­чайного процесса. Среди них особое место занимает второй сме­шанный центральный момент - корреляционная функция. Корре­ляционная функция характеризует статистическую связь между значениями случайного процесса в два различных момента вре­мени. Преобразование Фурье связывает ее со спектральной плотностью мощности случайного процесса. Это соотношение между корреляционной функцией и спектральной плотностью мощности лежит в основе корреляционного и спектрального ана­лиза случайных процессов.

В разделе рассматриваются n-мерные вероятностные характе­ристики случайного процесса.

16.1.Многомерная функция распределения и плотность распределения вероятностей случайного процесса

Двумерная ФРВ описывает случайный процесс ξ(t) в два момен­та времени t₁ и t₂ (рис. 16.1)

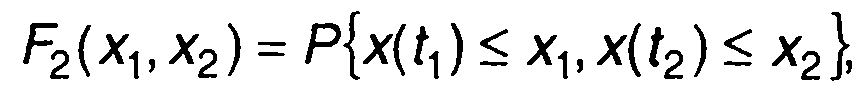(16.1)

где Р{...} - символ вероятности.

Функция F₂(x₁,x₂) определяет вероятность того, что случайный процесс ξ(t) в момент времени t1 не превышает уровень x₁ а в мо­мент времени t₂ - уровень х₂.

Рассматривая ансамбль реализаций случайного процесса, для двумерной ФРВ можно записать следующее предельное соотношение

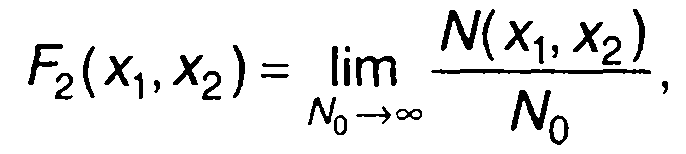(16.2)

где N₀ - общее число реализаций случайного процесса; N(x_b х₂) -

число реализаций, значения которых не превышают х₁ в момент времени U и х₂ в момент времени t₂.

В общем случае двумерная ФРВ зависит от двух выбранных значений уровня и двух моментов времени, в которые рассматри­вается случайный процесс. Для стационарного случайного процес­са ФРВ зависит не от рассматриваемых моментов времени, а от интервала между ними: т = t₂-t<_[ .

Двумерная ПРВ случайного процесса определяется как

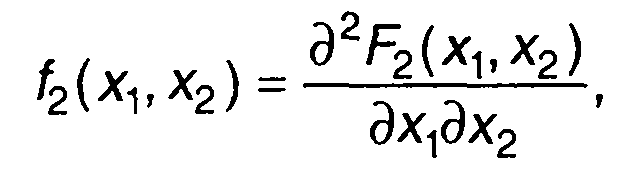(16.3)

если ФРВ имеет вторую производную. Она, как и ФРВ, зависит от значений х₁, х₂, t₁, t₂ (для стационарного случайного процесса - от интервала т между двумя моментами времени, в которые рассмат­ривается случайный процесс).

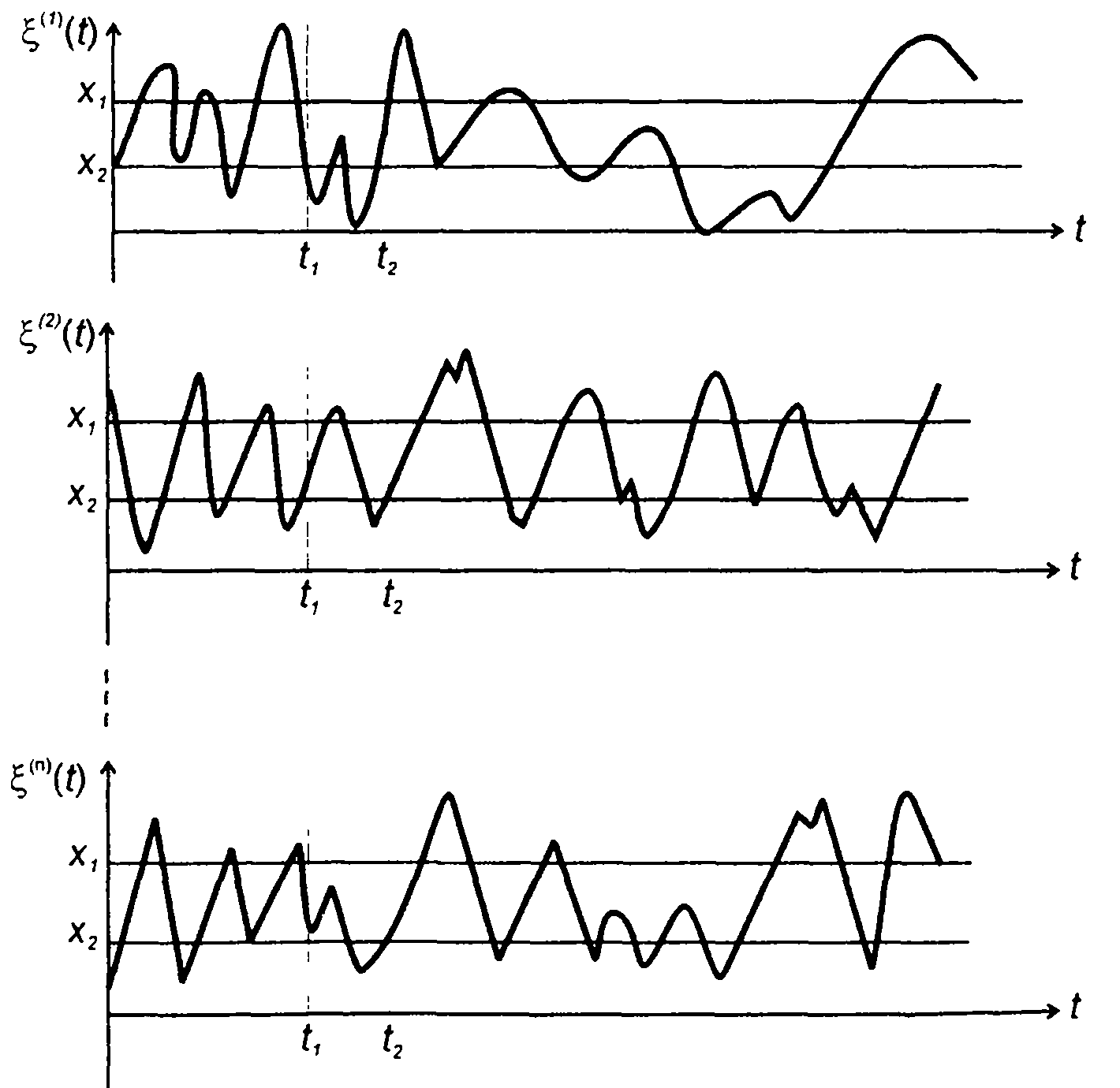
Рис. 16.1

ФРВ л-го порядка случайного процесса ξ(t) определяется как

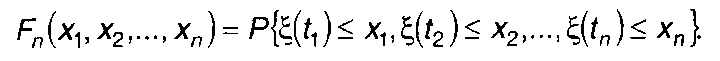(16.4)

Ей соответствует л-мерная ПРВ

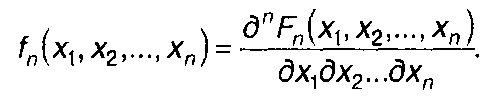(16.5)

ФРВ и ПРВ л-го порядка в общем случае зависят от л моментов времени .Для стационарного случайного процесса указанные ха­рактеристики зависят только от интервалов времени между рас­сматриваемыми моментами - всего n-1 интервал. В дальнейшем фигурируют только стационарные случайные процессы.

Чем выше порядок ФРВ (ПРВ), тем более детально она описы­вает случайный процесс. Однако в полной мере это справедливо только тогда, когда случайный процесс рассматривается на задан­ном ограниченном интервале времени.

Обозначим длительность выделяемого интервала времени Т (рис. 16.2). Если ФРВ описывает случайный процесс на заданном ин­тервале в моменты времени, отстоящие друг от друга на ∆t = Т/(n - 1): t₁, t₂ = t, + ∆t,...,t_n = t_n-1 + ∆t, то в этом случае n-мерная ФРВ (ПРВ) представляет тем более полную характеристику случайного про­цесса, чем больше л.

При n →∞

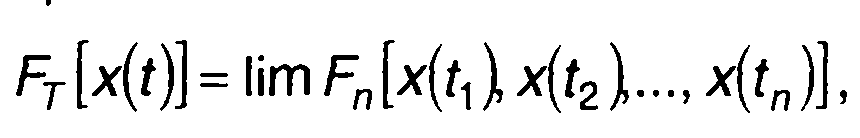(16.6)

если предел в (16.6) существует. Величина F_T[x(t)] представляет функционал распределения вероятностей случайного процесса на интервале времени. При x(t) = const функционал описывает вероят­ность непревышения случайным процессом заданного уровня на выбранном интервале времени.

От n-мерной ФРВ можно перейти к ФРВ более низких порядков

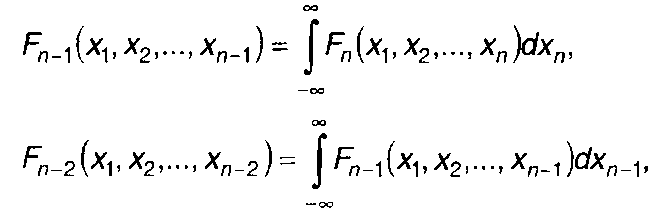(16.7)

и т. д.

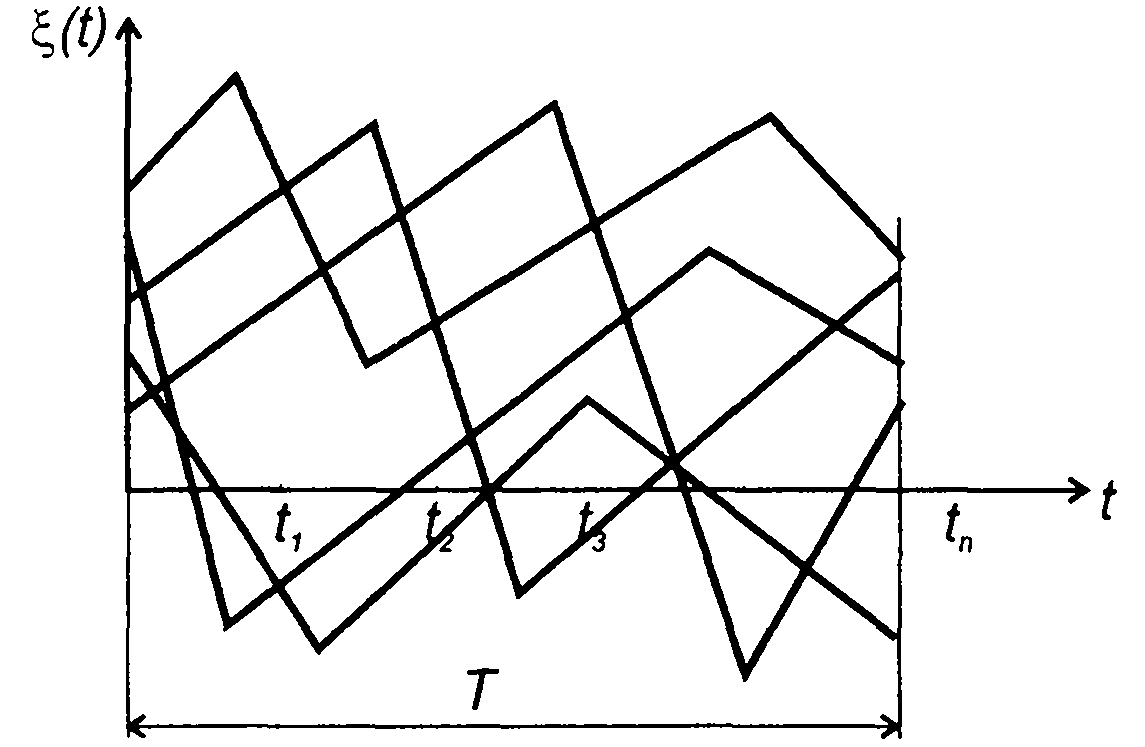
Рис. 16.2

ФРВ и ПРВ n-мерные позволяют получить моменты распределе­ния вероятностей случайного процесса: начальные моменты распределения

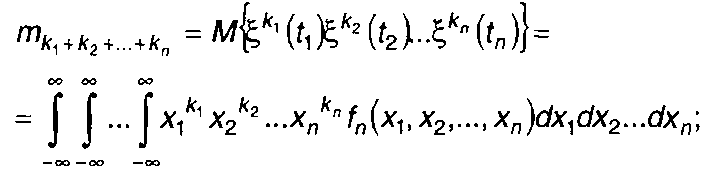(16.8)

центральные моменты распределения

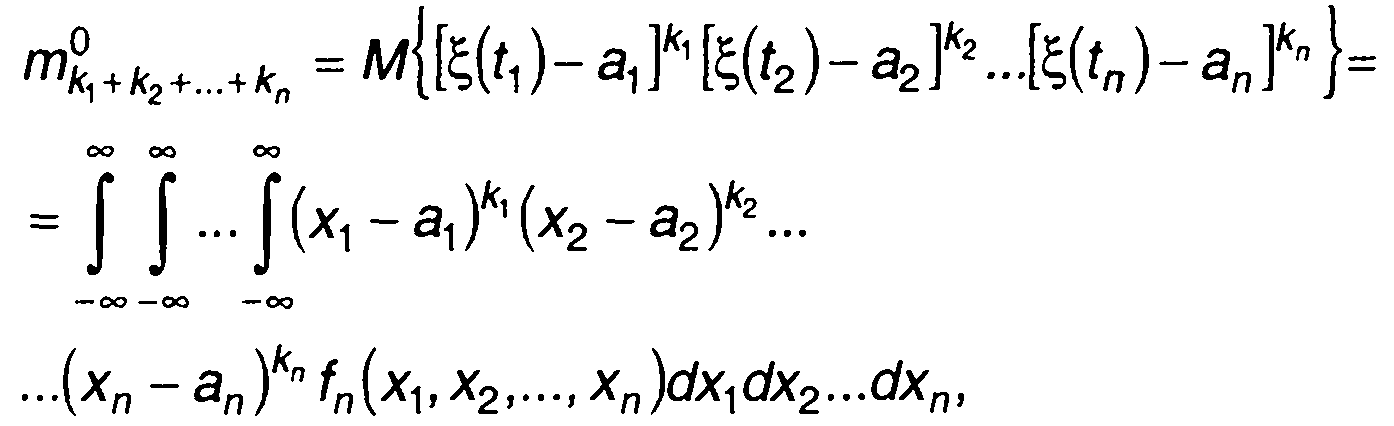(16.9)

где а₁ а₂,..., a_n - математические ожидания случайного процесса в моменты времени

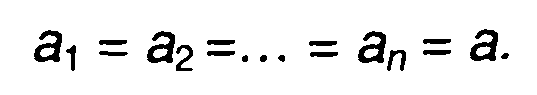
для стационарного случайного процесса

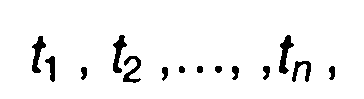
Важную роль при анализе случайных процессов играет второй смешанный центральный момент распределения вероятностей - корреляционная функция.

16.2. Корреляционная функция случайного процесса

16.2.1. Определение корреляционной функции

Второй смешанный начальный момент распределения вероят­ностей случайного процесса называется ковариационной функцией

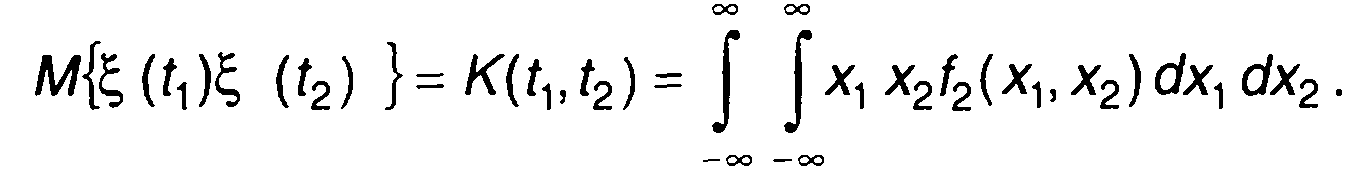(16.10)

Она получается усреднением произведения значений случайно­го процесса, взятых в моменты времени t₁ и t₂. Второй централь­ный момент распределения называется корреляционной функцией

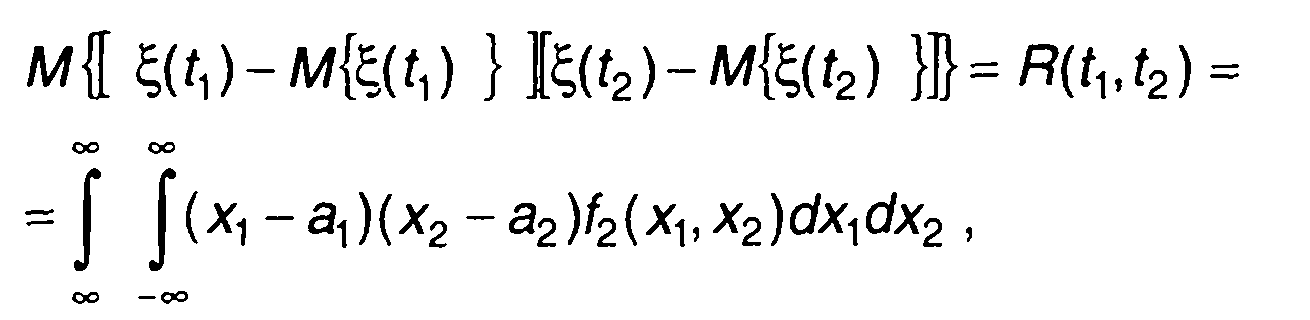(16.11)

где a1=M{ξ(t₁)], а₂ = M{ξ(t₂) } - математическое ожидание случай­ного процесса в моменты времени t₁ и t₂.

Подчеркивая, что характеристики относятся к одному случайно­му процессу, их называют автоковариационной и автокорреляцион­ной функциями.